(论文速读)FDConv:用于密集图像预测的频率动态卷积
论文题目:Frequency Dynamic Convolution for Dense Image Prediction(用于密集图像预测的频率动态卷积)
会议:
摘要:动态卷积(Dynamic Convolution, DY-Conv)通过多个并行权值与注意机制相结合实现自适应权值选择,显示出良好的性能,但这些权值的频率响应往往表现出高度相似性,导致参数成本高,但适应性有限。在这项工作中,我们引入了频率动态卷积(FDConv),这是一种通过在傅里叶域中学习固定参数预算来减轻这些限制的新方法。FDConv将该预算分成具有不相交傅立叶指标的基于频率的组,从而能够在不增加参数成本的情况下构建不同频率的权重。为了进一步增强自适应性,我们提出了核空间调制(KSM)和频带调制(FBM)。KSM在空间水平上动态调整各滤波器的频率响应,而FBM在频域上将权重分解为不同的频带,并根据局部内容动态调制。大量的物体检测、分割和分类实验验证了FDConv的有效性。我们证明,当应用于ResNet-50时,FDConv在适度增加+ 360万参数的情况下取得了优异的性能,优于之前需要大幅增加参数预算的方法(例如,CondConv +90M, KW +76.5M)。此外,FDConv可以无缝集成到各种架构中,包括ConvNeXt, swan - transformer,为现代视觉任务提供灵活高效的解决方案。
该代码可在https://github.com/LinweiChen/FDConv上公开获取。
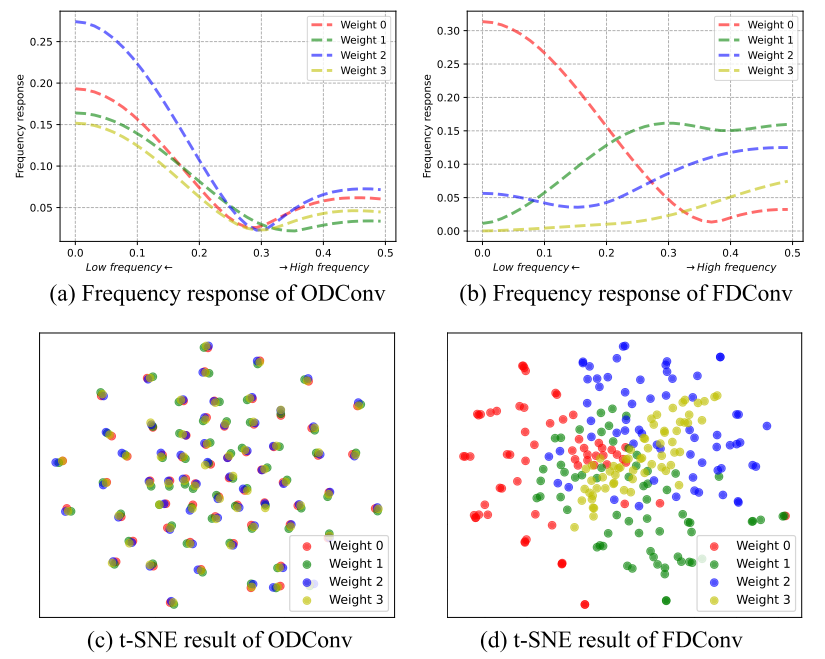
解释:权重频率响应和t-SNE分析。我们将权重的数量设置为4,以与ODConv对齐。(a) ODConv中四个平行权重的频率响应高度相似,表明多样性有限。(b)相比之下,FDConv对每个权重显示不同的频率响应,跨越频谱的不同部分。(c) ODConv的t-SNE图显示,四个权重中的过滤器紧密聚类,表明缺乏多样性。(d) FDConv的t-SNE图显示,四个权重的滤波器分布不同,多样性较大。
Frequency Dynamic Convolution (FDConv) - 从频率角度重新思考动态卷积
一、研究背景与问题分析
1.1 动态卷积的基本思想
动态卷积(Dynamic Convolution)是标准卷积的进化版本,通过使用多个并行权重结合注意力机制,实现样本特定的权重自适应。其基本公式为:
W = π₁W₁ + π₂W₂ + ... + πₙWₙ
其中{W₁, W₂, ..., Wₙ}是n个并行权重,{π₁, π₂, ..., πₙ}是动态生成的注意力系数。
1.2 现有方法的局限性
作者通过深入的频率分析,发现传统动态卷积方法存在三大核心问题:
问题1:频率响应高度相似
如图1所示,ODConv等方法的4个并行权重的频率响应曲线几乎重叠,缺乏频率多样性。
问题2:参数冗余严重
尽管参数量增加了4倍(如ODConv增加65.1M参数),但由于权重之间的相似性,这些额外参数并未带来相应的性能提升。
问题3:频率自适应能力有限
提取低频分量有助于抑制噪声,而高频分量对捕获细节和边界至关重要,但现有方法无法有效地自适应调整不同频段。
二、FDConv的创新设计
FDConv通过三个核心模块解决上述问题,整体框架如图2所示:
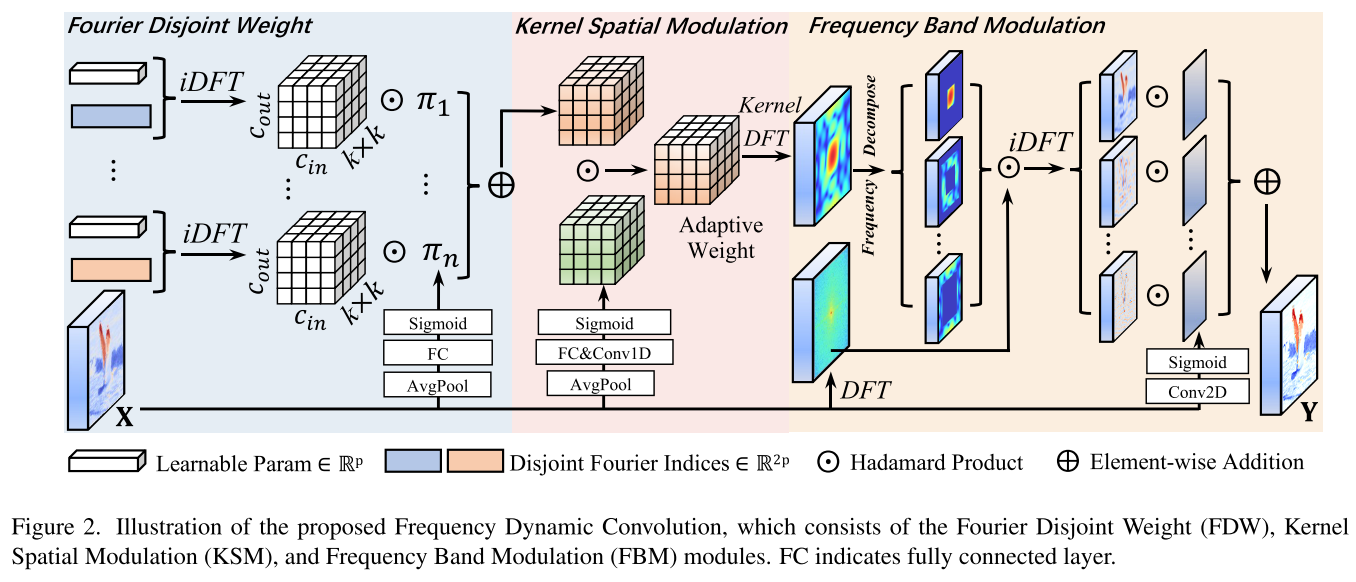
2.1 Fourier Disjoint Weight (FDW) - 傅里叶不相交权重
这是FDConv的核心创新,其设计理念是在频域而非空间域学习权重。
工作原理:
步骤1:傅里叶不相交分组
- 将固定的参数预算 k×k×Cᵢₙ×Cₒᵤₜ 重塑为 P ∈ ℝ^(kCᵢₙ×kCₒᵤₜ)
- 每个参数对应一个傅里叶索引(u,v)
- 根据频率大小||(u,v)||₂将参数排序,均匀划分为n个不相交的集合{P⁰, P¹, ..., Pⁿ⁻¹}
步骤2:傅里叶到空间域转换 使用逆离散傅里叶变换(iDFT):
Sⁱₚ,q = Σᵤ Σᵥ Pⁱᵤ,ᵥ exp(i2π(p/kCᵢₙ·u + q/kCₒᵤₜ·v))
步骤3:重组 将Sⁱ裁剪为k×k的patches并重组为标准权重形状 k×k×Cᵢₙ×Cₒᵤₜ
关键优势:
- ✅ 参数效率高:可以生成n>10个多样化权重,而不增加参数成本
- ✅ 频率多样性强:每个权重组只包含特定频段的分量,确保频率响应的多样性
- ✅ 零相似度:如图5(b)所示,生成的权重之间余弦相似度为0
2.2 Kernel Spatial Modulation (KSM) - 核空间调制
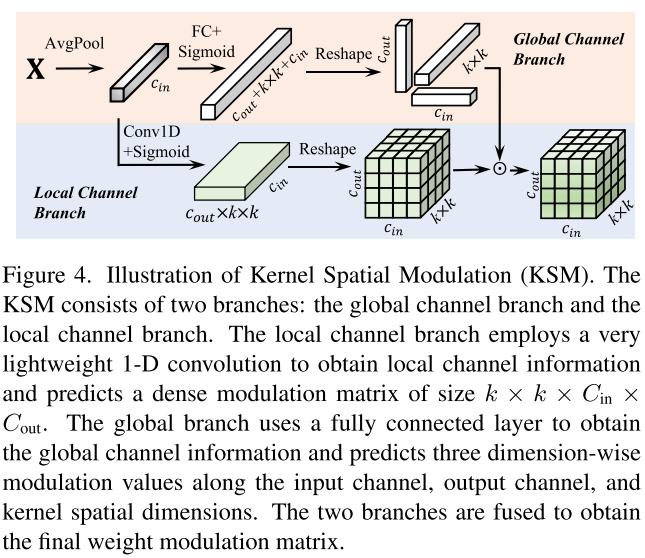
FDW的权重级混合较为粗糙,KSM通过预测密集调制矩阵 α ∈ ℝ^(k×k×Cᵢₙ×Cₒᵤₜ) 实现细粒度控制。
双分支架构:
局部通道分支
- 使用轻量级1-D卷积捕获局部通道信息
- 预测完整的调制矩阵(k×k×Cᵢₙ×Cₒᵤₜ)
- 显著降低参数量和计算复杂度
全局通道分支
- 使用全连接层获取全局通道信息
- 预测三个维度的调制值:输入通道、输出通道和核空间维度
2.3 Frequency Band Modulation (FBM) - 频段调制
FBM实现空间变化的频率调制,这是FDConv的另一大创新。
核心公式:
Y = Σᵦ (Aᵦ ⊙ (Wᵦ * X))
其中Aᵦ ∈ ℝ^(h×w)是第b个频段的空间调制图。
实现步骤:
1. 核频率分解 使用二值掩码Mᵦ分离特定频率范围: Wᵦ = F⁻¹(Mᵦ ⊙ F(W))
2. 频域卷积 根据卷积定理,在频域进行逐点乘法: Yᵦ = F⁻¹((Mᵦ ⊙ F(W)) ⊙ F(X))
3. 空间变化调制 通过标准卷积+Sigmoid生成调制图Aᵦ,实现不同空间位置的频率自适应
频段划分策略:
默认使用八度分区策略将频谱分为4个频段,阈值为{0, 1/16, 1/8, 1/4, 1/2}
三、实验结果与分析
3.1 主要实验结果
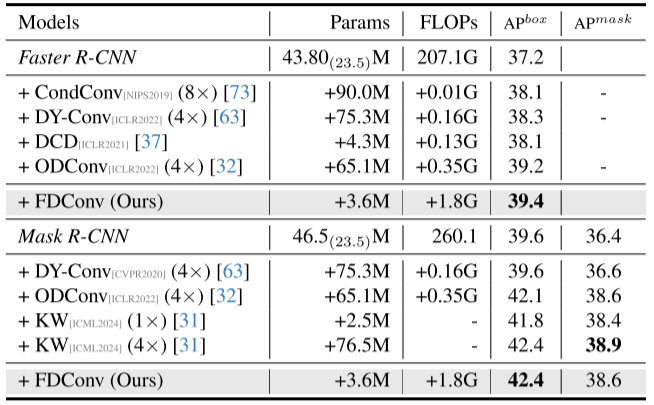
目标检测 (Faster R-CNN on COCO)
| 方法 | 参数增量 | FLOPs增量 | AP^box |
|---|---|---|---|
| Baseline | - | - | 37.2 |
| CondConv | +90.0M | +0.01G | 38.1 |
| ODConv | +65.1M | +0.35G | 39.2 |
| FDConv | +3.6M | +1.8G | 39.4 |
FDConv仅增加3.6M参数就达到39.4的AP^box,超越了需要大量参数的方法。
实例分割 (Mask R-CNN on COCO)
| 方法 | 参数增量 | AP^box | AP^mask |
|---|---|---|---|
| Baseline | - | 39.6 | 36.4 |
| ODConv (4×) | +65.1M | 42.1 | 38.6 |
| KW (4×) | +76.5M | 42.4 | 38.9 |
| FDConv | +3.6M | 42.4 | 38.6 |
FDConv以极少的参数增量达到与KW相当的性能。
语义分割 (UPerNet on ADE20K)
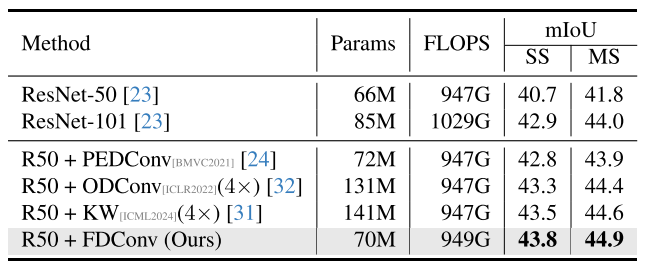
| 方法 | 参数总量 | mIoU (SS) | mIoU (MS) |
|---|---|---|---|
| ResNet-50 | 66M | 40.7 | 41.8 |
| R50 + ODConv | 131M | 43.3 | 44.4 |
| R50 + KW | 141M | 43.5 | 44.6 |
| R50 + FDConv | 70M | 43.8 | 44.9 |
FDConv在参数量仅为70M的情况下,取得了最高的mIoU分数。
3.2 跨架构适用性
现代架构集成
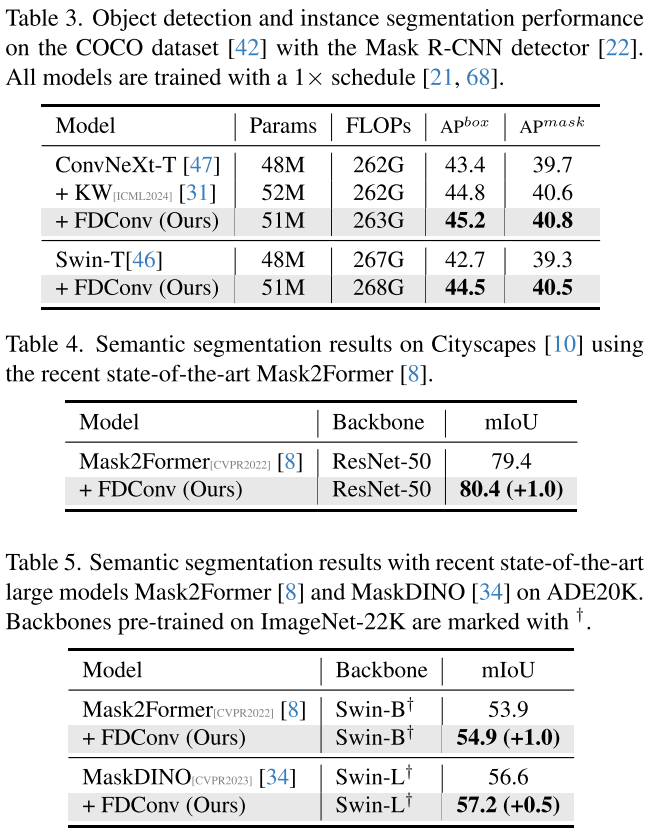
FDConv可无缝集成到ConvNeXt和Swin Transformer中,在ConvNeXt-T上AP^box达到45.2,在Swin-T上达到44.5。
大型模型增强
| 模型 | 骨干网络 | mIoU | 提升 |
|---|---|---|---|
| Mask2Former | ResNet-50 | 79.4 | - |
| + FDConv | ResNet-50 | 80.4 | +1.0 |
| MaskDINO | Swin-L | 56.6 | - |
| + FDConv | Swin-L | 57.2 | +0.5 |
在Cityscapes和ADE20K数据集上,FDConv为SOTA模型带来了稳定的性能提升。
3.3 深度分析
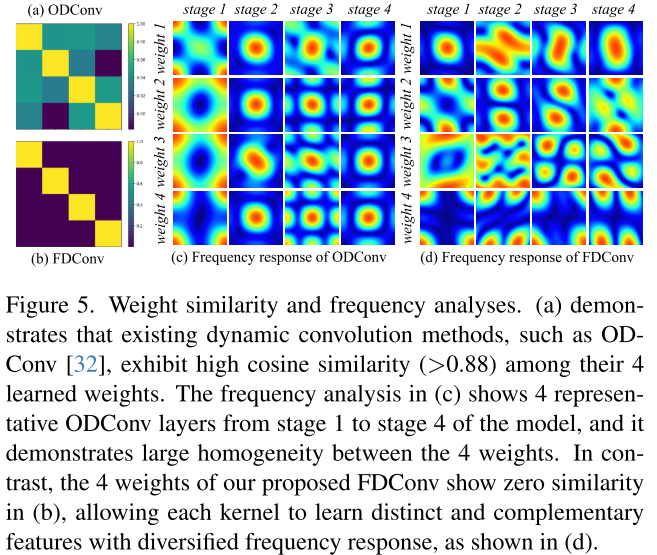
权重相似度分析
图5(a)显示ODConv的4个权重之间余弦相似度>0.88,而FDConv的权重相似度为0(图5(b)),证明了FDConv成功实现了权重多样性。
频率响应分析
图5(c)显示ODConv在不同stage的权重频率响应高度同质化,而FDConv展现出多样化的频率响应(图5(d))。
FBM可视化分析

图6显示,FBM的高频段调制值集中在物体边界,而低频段在物体内部有更高的调制值,这种选择性调制使得高频噪声被抑制,前景特征被增强。
四、技术亮点总结
4.1 创新性
- 首次从频率视角系统分析动态卷积的局限性
- 在傅里叶域构建权重,实现参数高效的频率多样化
- 空间变化的频率调制,突破传统动态卷积的空间不变性
4.2 实用性
- ✅ 参数效率极高:3.6M增量 vs. 竞争方法的60M-90M
- ✅ 即插即用:可集成到CNN和Transformer架构
- ✅ 性能提升显著:多个任务上超越SOTA方法
- ✅ 代码开源:便于研究和应用
4.3 理论贡献
- 傅里叶域参数分解:提供了新的权重多样化视角
- 频域卷积定理应用:巧妙解决了理想频率滤波器的无限支撑问题
- 多尺度频率自适应:在权重级、空间级和频段级实现三重自适应
五、局限性与未来展望
5.1 潜在局限
- FLOPs增加:虽然参数少,但FBM的频域操作增加了1.8G FLOPs
- 频段划分策略:当前使用固定的八度分区,可能不是最优策略
- iDFT计算:需要额外的傅里叶变换操作
5.2 未来方向
- 自适应频段划分:根据任务和数据自动学习最优频段
- 硬件优化:针对FFT/iDFT操作的专用加速
- 其他模态扩展:应用到视频、点云等数据
- 神经架构搜索:自动搜索最优的FDConv配置
六、结论
FDConv通过引入频率视角,成功解决了动态卷积领域长期存在的参数冗余和频率多样性不足问题。其核心创新——Fourier Disjoint Weight (FDW)、Kernel Spatial Modulation (KSM)和Frequency Band Modulation (FBM)——构成了一个完整的频率自适应框架。
实验证明,FDConv在目标检测、实例分割和语义分割等密集预测任务上取得了优异性能,同时保持了极高的参数效率。这项工作为构建更高效、更强大的视觉模型开辟了新方向。
关键启示:
- 频率域分析为神经网络设计提供了新视角
- 参数效率不仅取决于数量,更取决于多样性
- 空间自适应和频率自适应的结合是未来趋势
本文详细解析了FDConv的设计理念、技术细节和实验结果。如果你对频率域深度学习、动态网络或密集预测任务感兴趣,这篇论文值得深入研读!
