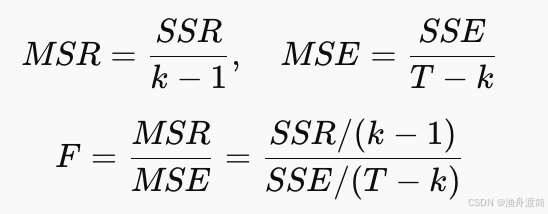机器学习-回归分析之一元线性回归
📘 机器学习-回归分析之一元线性回归
一、模型定义
当研究某一现象时,如果主要关注的是一个自变量(X)对一个因变量(Y)的影响,并且两者具有较强的线性相关关系,可采用一元线性回归模型(Simple Linear Regression Model)。
模型形式:Y=β0+β1X+ε
- ( Y ):因变量(被解释变量)
- ( X ):自变量(解释变量)
- ( β0 β1 ):模型参数(待估计)
- ( 𝜀):随机误差项
二、模型的主要假设
- 线性关系假设:Y与X呈线性关系。
- 独立性假设:各样本之间相互独立。
- 同方差性假设:误差项方差相同。
- 正态性假设:误差项服从均值为0、方差为σ²的正态分布。
三、参数估计方法
1. 最小二乘法(Ordinary Least Squares, OLS)
目标:通过样本数据,估计出最能代表总体规律的参数 β₀ 和 β₁。
- 思想:通过观测样本数据,寻找能最小化“预测值与实际值之间偏差平方和”的参数 𝛽0,𝛽1
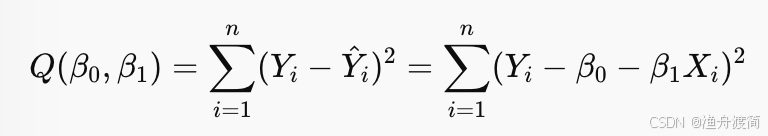
- 最小化问题求解过程:为了得到最佳参数,使得误差平方和最小化,
对 𝛽0,𝛽1β0,β1分别求偏导,并令导数为0,求导 → 联立方程 → 解得:
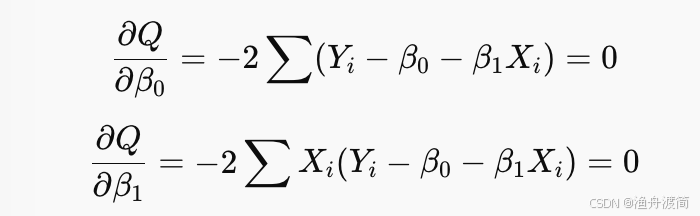
补充偏导数知识:
1)外层平方 → 用到导数公式 (g(x))^2’ = 2g(x)g’(x)
2)对 β₀ 求导时,β₁、Xᵢ、Yᵢ 都是常数
解这两个方程可得:
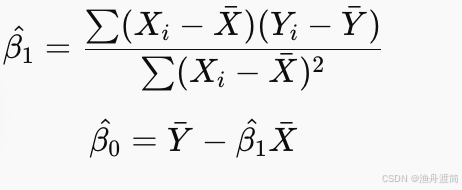
2、最大似然估计
最大似然估计(Maximum Likelihood Estimation, MLE)
是一种利用样本数据来估计总体分布参数的方法。
它基于“已知样本服从某种分布,但未知参数”的前提,通过选择使样本出现的概率最大化的参数值,作为参数估计结果。
- 基本思想与直观理解
1️⃣ 假设样本来自某个分布族,例如:
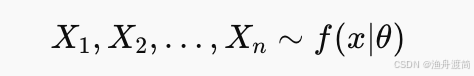
其中 θ是未知参数。
2️⃣ 构建“似然函数”:
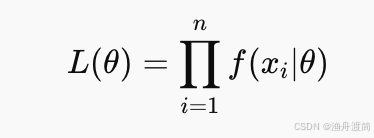
3️⃣ 取对数简化运算(对数似然函数):
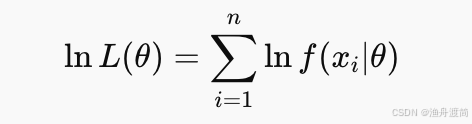
4️⃣ 对参数 (θ ) 求导并令导数为0(寻找极值点):
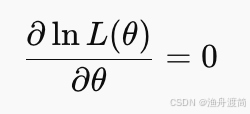
求得的 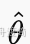
就是最大似然估计值。
- 举例:二项分布下的最大似然估计
假设掷硬币实验中,每次投掷成功(正面朝上)的概率为 ( p ),
观测到的成功次数 ( k ) 服从二项分布:
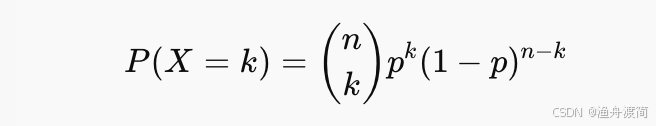
对应的似然函数为:
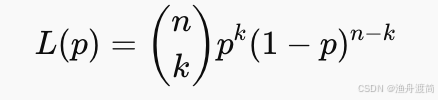
取对数求导:
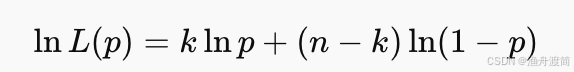
求偏导并令为0:
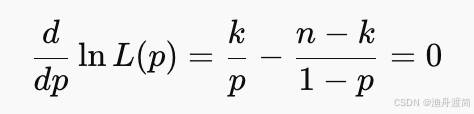
最终得到:
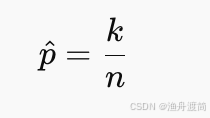
即样本中“成功次数比例”就是最大似然估计值。✅
-
MLE 在回归模型中的意义
-
在线性回归中,如果假设误差项服从正态分布 ,
则最小二乘法(OLS)与最大似然估计(MLE)在数学上是等价的。 -
在逻辑回归中,因变量服从二项分布,因此不能使用最小二乘法,而是必须使用最大似然估计法。
四、模型检验
1、参数估计:最小二乘估计(LSE)
已知两组数据 𝑥 和 𝑦,使用一元线性回归模型拟合两者之间的关系:
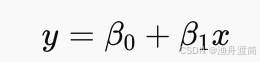
使用最小二乘法(LSE)估计回归方程的系数 ,得到最终回归方程。
已知:
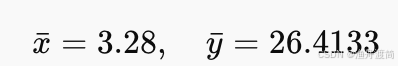
计算得到:
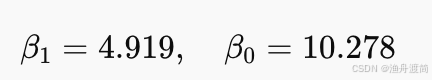
最终回归方程:
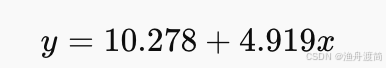
2、回归系数是否显著:t 检验
1️⃣ 检验目的
判断因变量 ( y ) 与自变量 ( x ) 是否存在线性关系,即:
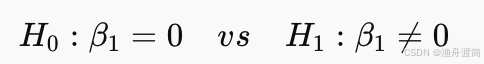
2️⃣ 检验水平
α=0.05或0.01
3️⃣ 构造统计量
若 (H0) 成立:
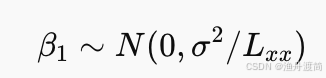
t 统计量定义为:
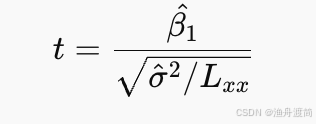
4️⃣ 判定规则
- 查 t 分布表,自由度 n - 2 = 13
- 双尾检验,显著性水平 α = 0.05
- 临界值:
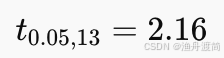
5️⃣ 结论
若 ( |t| > 2.16 ),拒绝 (H0),认为 x对 y有显著线性影响。
本次结果:拒绝原假设 (H0: β1= 0),接受 (H1: β1!=0)。
3、回归方程是否显著:F 检验
1️⃣ 检验目的
判断整个回归方程是否显著,即模型是否有统计意义。
根据平方和分解式:
SST = SSR + SSE
- (SST):总离差平方和(因变量的波动程度)
- (SSR):回归平方和(由自变量 (x) 引起的波动)
- (SSE):残差平方和(由其他因素引起的波动)
2️⃣ F统计量公式
3️⃣ 数据与计算结果
| 方差来源 | 自由度 | 平方和(SS) | 均方(MS) |
|---|---|---|---|
| 回归 | 1(即 (k-1)) | SSR = 841.65 | 841.65 |
| 残差 | 13(即 (T-k)) | SSE = 69.75 | 5.365 |
| 总和 | 14(即 (T-1)) | SST = 911.51 | — |
计算统计量:
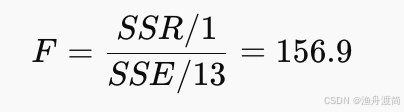
自由度 ((1, 13)),对应:
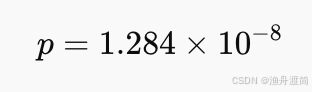
4️⃣ 检验结论

4、总结
| 检验方法 | 目的 | 结论 |
|---|---|---|
| t 检验 | 单个回归系数显著性 | β₁ 显著 ≠ 0 |
| F 检验 | 整体方程显著性 | 回归方程显著有效 |