「用Python来学微积分」21. 玩转高阶导数
文章目录
- 一、高阶导数的物理意义:从速度到加速度
- 手动求解示例:匀加速直线运动
- Python实现与可视化
- 二、基础高阶导数计算
- 幂函数的高阶导数
- Python验证
- 指数函数的高阶导数
- Python实现
- 三、复杂函数的高阶导数实战
- 复合函数求导:链式法则的应用
- Python验证
- 三角函数的高阶导数
- Python验证循环规律
- 四、参数方程的高阶导数
- 参数方程求导公式
- 手动求解示例:椭圆参数方程
- Python实现
- 摆线运动的高阶导数
- Python实现与验证
- 五、隐函数的高阶导数
- 六、总结与技巧
- 高阶导数的核心要点
- Python计算高阶导数的优势
- 学习建议
一、高阶导数的物理意义:从速度到加速度
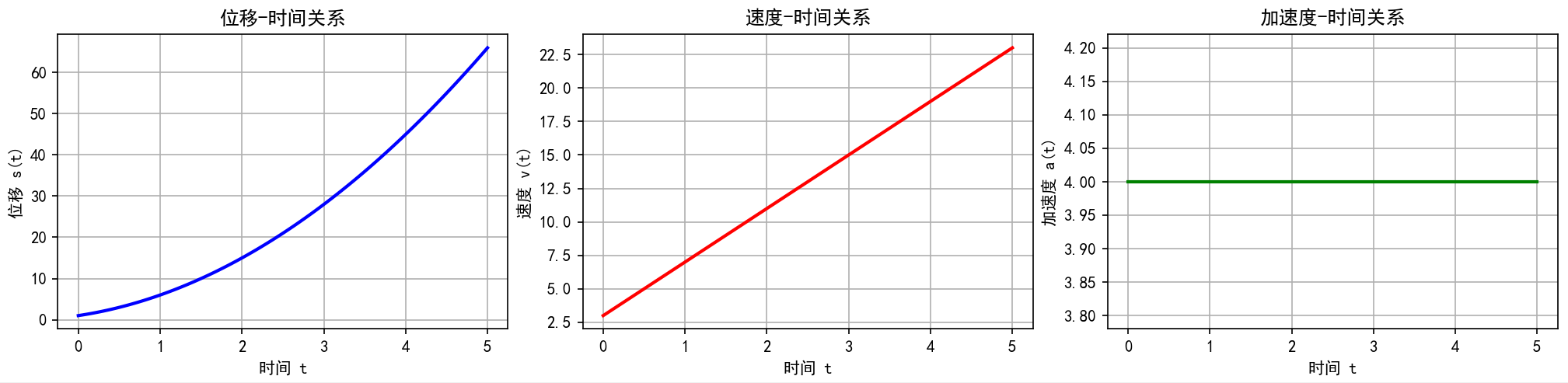
高阶导数的概念在物理学中有着直观的体现。当我们描述物体运动时,位移的一阶导数表示瞬时速度,二阶导数则表示加速度。这种变化率的层级关系揭示了自然界中运动的本质规律。
手动求解示例:匀加速直线运动
考虑一个质点做匀加速直线运动,其位移函数为:s(t)=2t2+3t+1s(t) = 2t^2 + 3t + 1s(t)=2t2+3t+1
手动求解过程:
- 一阶导数(速度):v(t)=dsdt=ddt(2t2+3t+1)=4t+3v(t) = \frac{ds}{dt} = \frac{d}{dt}(2t^2 + 3t + 1) = 4t + 3v(t)=dtds=dtd(2t2+3t+1)=4t+3
- 二阶导数(加速度):a(t)=dvdt=ddt(4t+3)=4a(t) = \frac{dv}{dt} = \frac{d}{dt}(4t + 3) = 4a(t)=dtdv=dtd(4t+3)=4
这表明该质点做匀加速直线运动,加速度恒为4个单位。
Python实现与可视化
import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, diff# 符号计算
t = symbols('t')
s = 2*t**2 + 3*t + 1
velocity = diff(s, t)
acceleration = diff(velocity, t)print(f"位移函数: s(t) = {s}")
print(f"速度函数: v(t) = {velocity}")
print(f"加速度函数: a(t) = {acceleration}")# 数值可视化
t_values = np.linspace(0, 5, 100)
s_values = 2*t_values**2 + 3*t_values + 1
v_values = 4*t_values + 3
a_values = np.full_like(t_values, 4) # 加速度恒为4fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 4))ax1.plot(t_values, s_values, 'b-', linewidth=2)
ax1.set_title('位移-时间关系')
ax1.set_xlabel('时间 t')
ax1.set_ylabel('位移 s(t)')
ax1.grid(True)ax2.plot(t_values, v_values, 'r-', linewidth=2)
ax2.set_title('速度-时间关系')
ax2.set_xlabel('时间 t')
ax2.set_ylabel('速度 v(t)')
ax2.grid(True)ax3.plot(t_values, a_values, 'g-', linewidth=2)
ax3.set_title('加速度-时间关系')
ax3.set_xlabel('时间 t')
ax3.set_ylabel('加速度 a(t)')
ax3.grid(True)plt.tight_layout()
plt.show()

二、基础高阶导数计算
幂函数的高阶导数
手动求解示例: y=x5y = x^5y=x5
手动求解过程:
- 一阶导数:dydx=5x4\frac{dy}{dx} = 5x^4dxdy=5x4
- 二阶导数:d2ydx2=20x3\frac{d^2y}{dx^2} = 20x^3dx2d2y=20x3
- 三阶导数:d3ydx3=60x2\frac{d^3y}{dx^3} = 60x^2dx3d3y=60x2
- n阶导数模式:y(n)=5!(5−n)!x5−ny^{(n)} = \frac{5!}{(5-n)!}x^{5-n}y(n)=(5−n)!5!x5−n(当n ≤ 5时)
Python验证
from sympy import symbols, diff, factorialx = symbols('x')
y = x**5print("幂函数的高阶导数:")
for n in range(1, 7):derivative = diff(y, x, n)print(f"y的{n}阶导数: {derivative}")

指数函数的高阶导数
手动求解示例: y=e2xy = e^{2x}y=e2x
手动求解过程:
- 一阶导数:dydx=2e2x\frac{dy}{dx} = 2e^{2x}dxdy=2e2x
- 二阶导数:d2ydx2=4e2x\frac{d^2y}{dx^2} = 4e^{2x}dx2d2y=4e2x
- 三阶导数:d3ydx3=8e2x\frac{d^3y}{dx^3} = 8e^{2x}dx3d3y=8e2x
- n阶导数通式:y(n)=2ne2xy^{(n)} = 2^n e^{2x}y(n)=2ne2x
Python实现
from sympy import exp, diff, symbolsx = symbols('x')
y_exp = exp(2*x)print("指数函数的高阶导数:")
for n in range(1, 5):deriv = diff(y_exp, x, n)print(f"y的{n}阶导数: {deriv}")
执行结果:

三、复杂函数的高阶导数实战
复合函数求导:链式法则的应用
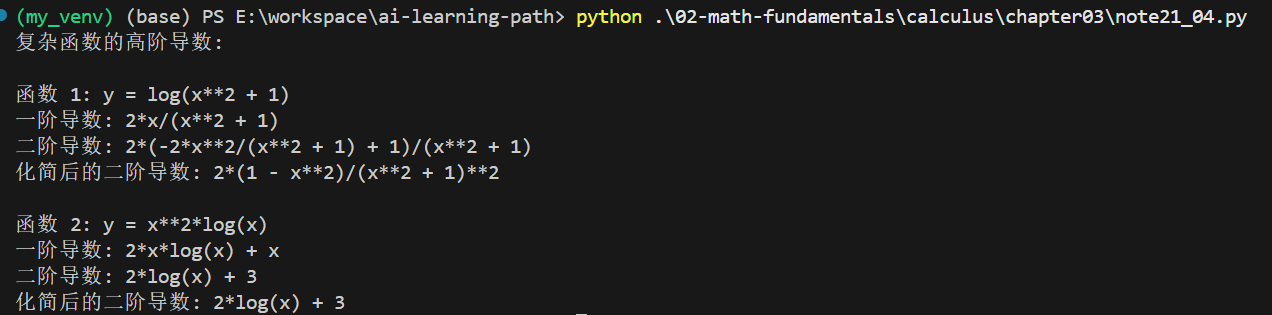
手动求解示例: y=ln(1+x2)y = \ln(1 + x^2)y=ln(1+x2)
手动求解过程:
-
一阶导数: dydx=11+x2⋅2x=2x1+x2\frac{dy}{dx} = \frac{1}{1+x^2} \cdot 2x = \frac{2x}{1+x^2}dxdy=1+x21⋅2x=1+x22x
-
二阶导数(使用商法则): d2ydx2=2(1+x2)−2x⋅2x(1+x2)2=2+2x2−4x2(1+x2)2=2−2x2(1+x2)2\frac{d^2y}{dx^2} = \frac{2(1+x^2) - 2x \cdot 2x}{(1+x^2)^2} = \frac{2 + 2x^2 - 4x^2}{(1+x^2)^2} = \frac{2 - 2x^2}{(1+x^2)^2}dx2d2y=(1+x2)22(1+x2)−2x⋅2x=(1+x2)22+2x2−4x2=(1+x2)22−2x2
Python验证
from sympy import log, sin, cos, sqrt, atanfunctions = [log(1 + x**2), # y = ln(1+x²)x**2 * log(x) # y = x² * ln(x)
]print("复杂函数的高阶导数:")
for i, func in enumerate(functions, 1):print(f"\n函数 {i}: y = {func}")first_deriv = diff(func, x)second_deriv = diff(func, x, 2)print(f"一阶导数: {first_deriv}")print(f"二阶导数: {second_deriv}")print(f"化简后的二阶导数: {second_deriv.simplify()}")
执行结果:
三角函数的高阶导数
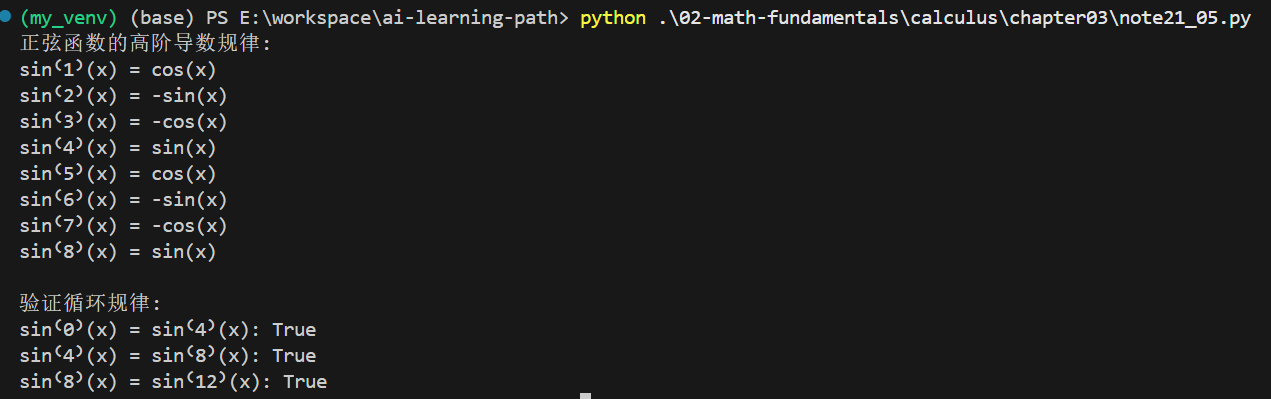
手动求解示例: y=sin(x)y = \sin(x)y=sin(x)
手动求解过程:
- 一阶导数:y′=cos(x)y' = \cos(x)y′=cos(x)
- 二阶导数:y′′=−sin(x)y'' = -\sin(x)y′′=−sin(x)
- 三阶导数:y′′′=−cos(x)y''' = -\cos(x)y′′′=−cos(x)
- 四阶导数:y(4)=sin(x)y^{(4)} = \sin(x)y(4)=sin(x)
- 规律:每4阶循环一次
Python验证循环规律
y_sin = sin(x)print("正弦函数的高阶导数规律:")
for n in range(1, 9):derivative = diff(y_sin, x, n)print(f"sin⁽{n}⁾(x) = {derivative}")# 验证循环规律
print("\n验证循环规律:")
for n in range(0, 9, 4):derivative_n = diff(y_sin, x, n)derivative_n_plus_4 = diff(y_sin, x, n+4)print(f"sin⁽{n}⁾(x) = sin⁽{n+4}⁾(x): {derivative_n.equals(derivative_n_plus_4)}")
运行结果:
四、参数方程的高阶导数
参数方程求导是高阶导数应用中的重要内容,特别在描述曲线运动和几何形状时非常有用。
参数方程求导公式
对于参数方程:x=f(t),y=g(t)x = f(t), y = g(t)x=f(t),y=g(t)
- 一阶导数:dydx=dydtdxdt\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}dxdy=dtdxdtdy
- 二阶导数:d2ydx2=ddt(dydx)dxdt\frac{d^2y}{dx^2} = \frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}}dx2d2y=dtdxdtd(dxdy)
手动求解示例:椭圆参数方程
给定参数方程:x=acos(t),y=bsin(t)x = a\cos(t), y = b\sin(t)x=acos(t),y=bsin(t)
手动求解过程:
-
一阶导数: dxdt=−asin(t),dydt=bcos(t)\frac{dx}{dt} = -a\sin(t), \quad \frac{dy}{dt} = b\cos(t)dtdx=−asin(t),dtdy=bcos(t) dydx=bcos(t)−asin(t)=−bacot(t)\frac{dy}{dx} = \frac{b\cos(t)}{-a\sin(t)} = -\frac{b}{a}\cot(t)dxdy=−asin(t)bcos(t)=−abcot(t)
-
二阶导数: ddt(dydx)=ddt(−bacot(t))=bacsc2(t)\frac{d}{dt}\left(\frac{dy}{dx}\right) = \frac{d}{dt}\left(-\frac{b}{a}\cot(t)\right) = \frac{b}{a}\csc^2(t)dtd(dxdy)=dtd(−abcot(t))=abcsc2(t) d2ydx2=bacsc2(t)−asin(t)=−ba2csc3(t)\frac{d^2y}{dx^2} = \frac{\frac{b}{a}\csc^2(t)}{-a\sin(t)} = -\frac{b}{a^2}\csc^3(t)dx2d2y=−asin(t)abcsc2(t)=−a2bcsc3(t)
Python实现
from sympy import symbols, diff, sin, cos, cot, csct, a, b = symbols('t a b')
x_ellipse = a * cos(t)
y_ellipse = b * sin(t)# 一阶导数
dx_dt = diff(x_ellipse, t)
dy_dt = diff(y_ellipse, t)
dy_dx = dy_dt / dx_dt# 二阶导数
d2y_dx2 = diff(dy_dx, t) / dx_dtprint("椭圆参数方程的高阶导数:")
print(f"x = {x_ellipse}, y = {y_ellipse}")
print(f"一阶导数 dy/dx = {dy_dx.simplify()}")
print(f"二阶导数 d²y/dx² = {d2y_dx2.simplify()}")
运行结果:

摆线运动的高阶导数
手动求解示例: 摆线方程 x=a(t−sint),y=a(1−cost)x = a(t - \sin t), y = a(1 - \cos t)x=a(t−sint),y=a(1−cost)
手动求解过程:
-
一阶导数: dxdt=a(1−cost),dydt=asint\frac{dx}{dt} = a(1 - \cos t), \quad \frac{dy}{dt} = a\sin tdtdx=a(1−cost),dtdy=asint dydx=asinta(1−cost)=sint1−cost\frac{dy}{dx} = \frac{a\sin t}{a(1 - \cos t)} = \frac{\sin t}{1 - \cos t}dxdy=a(1−cost)asint=1−costsint
利用三角恒等式化简:sint1−cost=cot(t2)\frac{\sin t}{1 - \cos t} = \cot\left(\frac{t}{2}\right)1−costsint=cot(2t)
-
二阶导数: ddt(dydx)=ddt(cot(t2))=−12csc2(t2)\frac{d}{dt}\left(\frac{dy}{dx}\right) = \frac{d}{dt}\left(\cot\left(\frac{t}{2}\right)\right) = -\frac{1}{2}\csc^2\left(\frac{t}{2}\right)dtd(dxdy)=dtd(cot(2t))=−21csc2(2t) d2ydx2=−12csc2(t2)a(1−cost)\frac{d^2y}{dx^2} = \frac{-\frac{1}{2}\csc^2\left(\frac{t}{2}\right)}{a(1 - \cos t)}dx2d2y=a(1−cost)−21csc2(2t)
利用三角恒等式 1−cost=2sin2(t/2)1 - \cos t = 2 \sin^2(t/2)1−cost=2sin2(t/2) 和 csc(t/2)=1/sin(t/2)\csc(t/2) = 1/\sin(t/2)csc(t/2)=1/sin(t/2) 进行化简: d2ydx2=−12csc2(t2)a⋅2sin2(t/2)=−12csc2(t2)2asin2(t/2)=−14asin2(t/2)⋅csc2(t/2)(将常数部分合并)=−14asin4(t/2)(因为 csc2(t/2)=1/sin2(t/2))=−1a(2sin2(t/2))2(将分母写成平方形式)=−1a(1−cost)2(因为 2sin2(t/2)=1−cost)\begin{align*} \frac{d^2y}{dx^2} &= \frac{ -\frac{1}{2}\csc^2\left(\frac{t}{2}\right) }{ a \cdot 2 \sin^2(t/2) } \\ &= \frac{ -\frac{1}{2}\csc^2\left(\frac{t}{2}\right) }{ 2a \sin^2(t/2) } \\ &= \frac{ -1 }{ 4a \sin^2(t/2) } \cdot \csc^2(t/2) \quad \text{(将常数部分合并)} \\ &= \frac{ -1 }{ 4a \sin^4(t/2) } \quad \text{(因为 $\csc^2(t/2) = 1/\sin^2(t/2)$)} \\ &= \frac{ -1 }{ a (2\sin^2(t/2))^2 } \quad \text{(将分母写成平方形式)} \\ &= \frac{ -1 }{ a (1 - \cos t)^2 } \quad \text{(因为 $2\sin^2(t/2) = 1 - \cos t$)} \end{align*}dx2d2y=a⋅2sin2(t/2)−21csc2(2t)=2asin2(t/2)−21csc2(2t)=4asin2(t/2)−1⋅csc2(t/2)(将常数部分合并)=4asin4(t/2)−1(因为 csc2(t/2)=1/sin2(t/2))=a(2sin2(t/2))2−1(将分母写成平方形式)=a(1−cost)2−1(因为 2sin2(t/2)=1−cost)
Python实现与验证
# 摆线参数方程
x_cycloid = a * (t - sin(t))
y_cycloid = a * (1 - cos(t))# 求导计算
dx_dt_cycloid = diff(x_cycloid, t)
dy_dt_cycloid = diff(y_cycloid, t)
dy_dx_cycloid = dy_dt_cycloid / dx_dt_cycloid# 二阶导数
d2y_dx2_cycloid = diff(dy_dx_cycloid, t) / dx_dt_cycloidprint("摆线方程的高阶导数:")
print(f"x = {x_cycloid}")
print(f"y = {y_cycloid}")
print(f"一阶导数: {dy_dx_cycloid.simplify()}")
print(f"二阶导数: {d2y_dx2_cycloid.simplify()}")
运行结果:

五、隐函数的高阶导数
隐函数求导法用于处理无法显式表示为y=f(x)的函数关系。
手动求解示例:x2+y2−xy=1x^2 + y^2 - xy = 1x2+y2−xy=1
手动求解过程:
-
一阶导数(两边对x求导): 2x+2ydydx−(y+xdydx)=02x + 2y\frac{dy}{dx} - (y + x\frac{dy}{dx}) = 02x+2ydxdy−(y+xdxdy)=0 (2y−x)dydx=y−2x(2y - x)\frac{dy}{dx} = y - 2x(2y−x)dxdy=y−2x dydx=y−2x2y−x\frac{dy}{dx} = \frac{y - 2x}{2y - x}dxdy=2y−xy−2x
-
二阶导数: 对一阶导数两边再对x求导: d2ydx2=[(y′−2)(2y−x)−(y−2x)(2y′−1)](2y−x)2\frac{d^2y}{dx^2} = \frac{[(y' - 2)(2y - x) - (y - 2x)(2y' - 1)]}{(2y - x)^2}dx2d2y=(2y−x)2[(y′−2)(2y−x)−(y−2x)(2y′−1)] 代入y′=y−2x2y−xy' = \frac{y - 2x}{2y - x}y′=2y−xy−2x并化简。
首先,分别处理分子中的两项:
- 第一项:(y−2x2y−x−2)(2y−x)=(y−2x−2(2y−x)2y−x)(2y−x)=−3y\left( \frac{y - 2x}{2y - x} - 2 \right)(2y - x) = \left( \frac{y - 2x - 2(2y - x)}{2y - x} \right)(2y - x) = -3y(2y−xy−2x−2)(2y−x)=(2y−xy−2x−2(2y−x))(2y−x)=−3y
- 第二项:(y−2x)(2⋅y−2x2y−x−1)=(y−2x)(2y−4x−(2y−x)2y−x)=−3x(y−2x)2y−x(y - 2x) \left( 2\cdot\frac{y - 2x}{2y - x} - 1 \right) = (y - 2x) \left( \frac{2y - 4x - (2y - x)}{2y - x} \right) = \frac{-3x(y - 2x)}{2y - x}(y−2x)(2⋅2y−xy−2x−1)=(y−2x)(2y−x2y−4x−(2y−x))=2y−x−3x(y−2x)
因此,整个分子为: 分子=(−3y)−(−3x(y−2x)2y−x)=−3y+3x(y−2x)2y−x\text{分子} = (-3y) - \left( \frac{-3x(y - 2x)}{2y - x} \right) = -3y + \frac{3x(y - 2x)}{2y - x}分子=(−3y)−(2y−x−3x(y−2x))=−3y+2y−x3x(y−2x) 通分后合并: 分子=−3y(2y−x)+3x(y−2x)2y−x=−6y2+3xy+3xy−6x22y−x=−6(x2−xy+y2)2y−x\text{分子} = \frac{-3y(2y - x) + 3x(y - 2x)}{2y - x} = \frac{-6y^2 + 3xy + 3xy - 6x^2}{2y - x} = \frac{-6(x^2 - xy + y^2)}{2y - x}分子=2y−x−3y(2y−x)+3x(y−2x)=2y−x−6y2+3xy+3xy−6x2=2y−x−6(x2−xy+y2)
最终,二阶导数为: d2ydx2=−6(x2−xy+y2)2y−x(2y−x)2=−6(x2−xy+y2)(2y−x)3=6(x2−xy+y2)x3−6x2y+12xy2−8y3\frac{d^2y}{dx^2} = \frac{ \frac{-6(x^2 - xy + y^2)}{2y - x} }{ (2y - x)^2 } = -\frac{6(x^2 - xy + y^2)}{(2y - x)^3} = \frac{6(x^2 - xy + y^2)}{x^3 - 6x^2y + 12x y^2 - 8y^3}dx2d2y=(2y−x)22y−x−6(x2−xy+y2)=−(2y−x)36(x2−xy+y2)=x3−6x2y+12xy2−8y36(x2−xy+y2) 这个结果也可以通过因式分解,写成与Python输出一致的形式 6(x2−xy+y2)(x−2y)3\frac{6(x^2 - xy + y^2)}{(x - 2y)^3}(x−2y)36(x2−xy+y2)。
Python实现
from sympy import Function, Eq, solvey_func = Function('y')(x)
equation = x**2 + y_func**2 - x*y_func - 1# 一阶导数
deriv_eq1 = diff(equation, x)
y_prime = solve(deriv_eq1, diff(y_func, x))# 二阶导数
deriv_eq2 = diff(deriv_eq1, x)
y_double_prime = solve(deriv_eq2, diff(y_func, x, 2))# 替换一阶导数
y_double_prime_simplified = y_double_prime.subs(diff(y_func, x), y_prime)print("隐函数的高阶导数:")
print(f"方程: {equation} = 0")
print(f"一阶导数: dy/dx = {y_prime}")
print(f"二阶导数: d²y/dx² = {y_double_prime_simplified.simplify()}")

六、总结与技巧
高阶导数的核心要点
- 物理意义明确:位置→速度→加速度的递进关系体现了高阶导数的实际价值
- 数学本质清晰:导数的导数,描述变化率的变化率
- 计算技巧多样:链式法则、乘积法则、参数方程求导法等
Python计算高阶导数的优势
- 符号计算:SymPy可以进行精确的符号运算,避免数值误差
- 数值验证:SciPy等库提供数值方法,验证符号计算结果的正确性
- 可视化展示:Matplotlib等库可以直观展示高阶导数的几何意义
学习建议
- 掌握基本公式:熟记常见函数的n阶导数公式
- 理解物理背景:将数学概念与物理现象联系起来
- 多练习手算:在理解的基础上进行手动推导
- 善用工具验证:使用Python验证手算结果,提高准确性
通过本文的学习,你不仅掌握了高阶导数的理论知识,还学会了如何使用Python进行符号计算和数值验证。这种结合传统数学推导与现代计算工具的学习方法,将帮助你更深入地理解微积分的精髓。
专栏导航目录 《程序员AI之路:从Python起步》完全学习导航
完整代码已开源 ai-learning-path,欢迎Star和Fork!
下节预告:在下一篇文章中,我们将开始学习微分中值定理,包括费马定理、罗马定理、拉格朗日定理等。
参考资料:
- 扈志明《微积分》教材
互动邀请:如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!
