C语言之递归函数
目录
函数和类型
阶乘
█递归函数调用
函数中可以调用和该函数自身完全相同的函数,这样的调用方式称为递归函数调用,下面我们就来学习相关的基础知识。
函数和类型
所谓递归(recursive),就是将自己包含在内,或者用自己来定义自己。
我们用下面的图来说明:(ps:引用知乎@是花花吖图片)
显示器里面套着一个又一个显示器
通过采用递归的思考方式,从1开始无限延续的自然数1、2、3……就可以像下面这样使用有限的方式定义出来:
█自然数的定义
a 1是自然数
b 某个自然数后面的整数也是自然数
通过使用递归定义,无限存在的自然数就可以通过两个语句定义出来,不仅仅是定义,通过有效利用递归还可以使程序更加整洁。
阶乘
递归的另一个例子,就是求非负整数的阶乘。对于非负整数n的阶乘,可以采用如下方式进行定义:
█阶乘n!的定义(n为非负整数)
a 0!= 1
b 若n > 0,则n!= n*(n-1)!
例如,5的阶乘5!可以通过5*4!求得,而4的阶乘4!可以通过4*3!求得一直到1!= 1*0!,根据定义0!= 1
我们用程序来实现,如下:
#include<stdio.h>
/*返回阶乘的值*/
int factorial(int n)
{
if(n > 0)
return n * factorial(n - 1);
else
return 1;
}
int main()
{
int num;
printf("请输入一个整数:");
scanf("%d", &num);
printf("%d的阶乘是%d\n", num, factorial(num));
return 0;
}只要形参接收的值大于0,函数factorical就会返回到n * factorial(n - 1),否则,返回到1.
看起来虽然很简单,但在程序执行时是十分复杂的,下面让我们来看看是如何执行的:
█递归函数调用
我们以求3的阶乘为例,看看函数factorical求阶乘的流程:
a 通过factorical(3)调用函数函数factorical,因此形参n会被传入3,所以该函数返回3*factorical(2),但是要知道函数factorical(2)的值,就必须以2为参数再次调用函数函数factorical。
b 被调用的函数函数factorical,将2传入形参n中,该函数返回2*factorical(1),想知道函数factorical(1),的值就必须以1为参数再次调用函数factorical
c 被调用的函数factorical,将1传入形参n中,为了进行1*factorical(0)的运算,调用函数函数factorical(0)
d 因为形参n接受到的值为0,所以函数factorical返回1
大家参照下面的流程图来对应上面每一个步骤:(红色箭头是参数,黄色箭头是返回值)
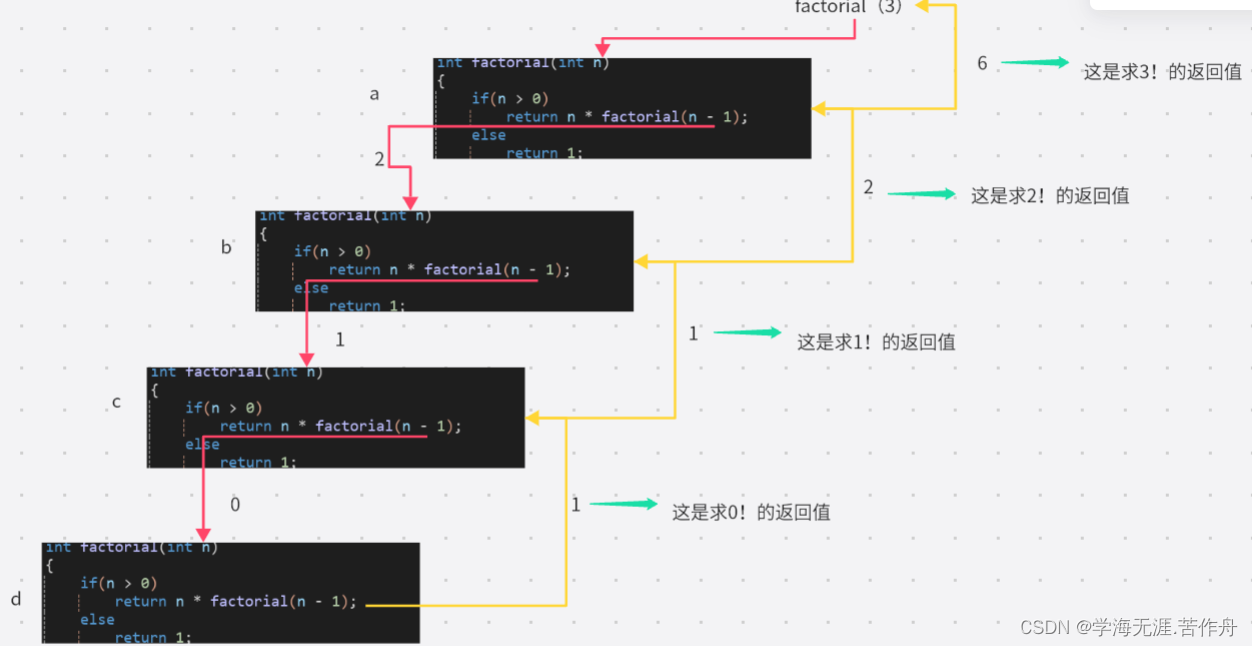
接下来是递归:大家可以从下面中仔细考虑下体现出的递归意义
c 收到返回值1的函数factorical,返回1*factorical(0),即1*1
b 收到返回值2的函数factorical,返回2*factorical(1),即2*1
d 收到返回值3的函数factorical,返回3*factorical(2),即3*2
为了求得n-1的阶乘,函数factorical调用函数factorical,像这样的函数调用称为递归函数调用
递归函数调用与其说时调用函数本身,倒不如理解为调用和该函数同样的函数更加自然,如果是调用函数本身,则会一直调用下去,进入死循环。
如果待处理的问题、函数或者数据结构已经具有递归定义,就可以使用递归算法。使用递归的方式求阶乘是为了大家能够更好地理解,但并不合适。
