分享MATLAB在数据分析与科学计算中的高效算法案例
MATLAB 是一种强大的语言和环境,广泛应用于数据分析和科学计算。这里分享一些常见的高效算法及其案例,这些算法可以帮助提升在 MATLAB 中进行数据分析与科学计算的效率。

如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
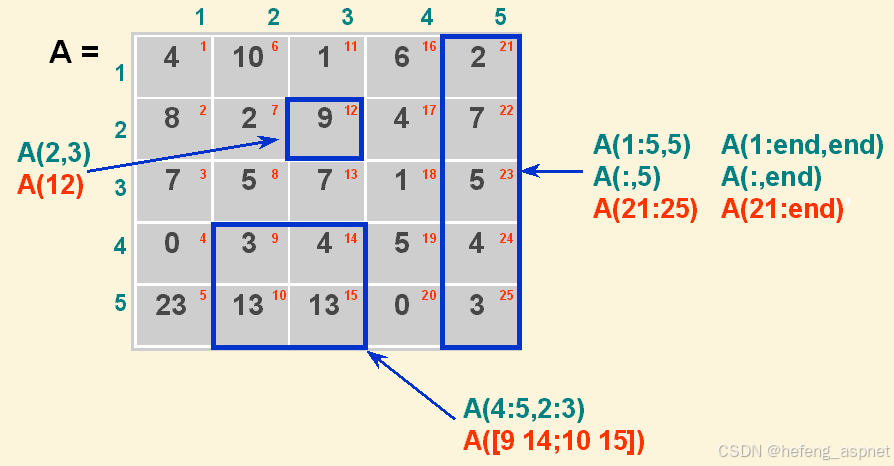
1. 基于矩阵的快速运算
案例:线性回归分析
线性回归是一个基本的数据分析任务,可以通过矩阵运算高效完成。在 MATLAB 中,可以使用矩阵乘法来计算线性回归的系数。
% 生成示例数据
X = [ones(100, 1), (1:100)']; % 设计矩阵,包含偏置项
y = 3 + 2 * (1:100)' + randn(100, 1); % 目标变量
% 使用正规方程求解线性回归系数
theta = (X' * X) \ (X' * y);
% 显示系数
disp(theta);
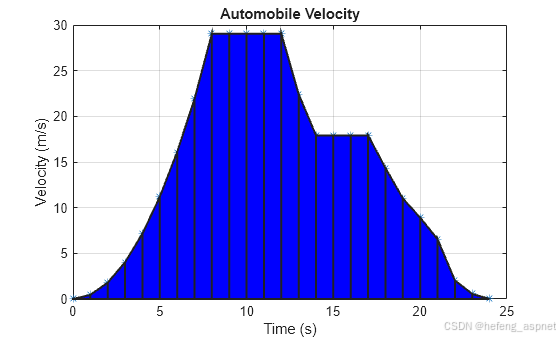
2. 数值积分
案例:使用 `integral` 函数进行数值积分
在科学计算中,数值积分是一个常见问题。MATLAB 提供了 `integral` 函数,可以高效计算一维函数的积分。
f = @(x) sin(x).^2; % 定义要积分的函数
a = 0; % 积分下限
b = pi; % 积分上限
% 计算积分
result = integral(f, a, b);
disp(result);
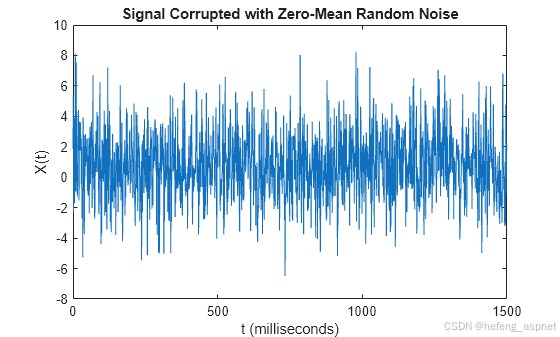
3. 使用 `fft` 进行快速傅里叶变换
案例:信号处理
傅里叶变换常用于信号分析,MATLAB 中的 `fft` 函数实现了高效的快速傅里叶变换。
% 生成示例信号
fs = 1000; % 采样频率
t = 0:1/fs:1-1/fs; % 时间向量
f = 50; % 信号频率
signal = cos(2 * pi * f * t) + randn(size(t)) * 0.5; % 正弦信号加噪声
% 计算傅里叶变换
Y = fft(signal);
P2 = abs(Y/length(signal)); % 双边谱
P1 = P2(1:length(signal)/2+1); % 单边谱
P1(2:end-1) = 2*P1(2:end-1); % 归一化
% 显示频率
f = fs*(0:(length(signal)/2))/length(signal);
plot(f, P1);
title('单边振幅谱');
xlabel('频率 (Hz)');
ylabel('|P1(f)|');
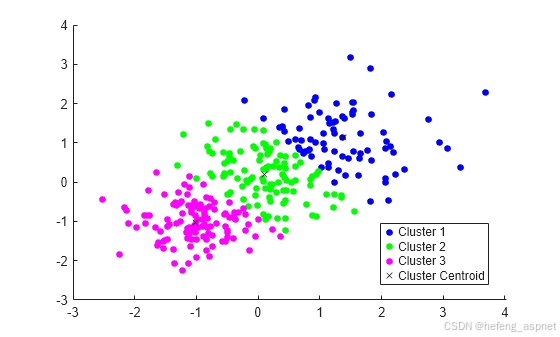
4. K-means 聚类
案例:数据聚类
可以使用 K-means 算法对数据集进行聚类分析,MATLAB 提供了 `kmeans` 函数来实现这一算法。
% 生成示例数据
data = [randn(100, 2) + 5; randn(100, 2) - 5]; % 两个聚类
k = 2; % 聚类数目
% 执行 K-means 聚类
[idx, centroids] = kmeans(data, k);
% 绘制结果
figure;
gscatter(data(:,1), data(:,2), idx);
hold on;
plot(centroids(:,1), centroids(:,2), 'kx', 'MarkerSize', 15, 'LineWidth', 3);
title('K-means 聚类结果');
xlabel('特征 1');
ylabel('特征 2');
5. 优化算法
案例:使用 `fminunc` 进行无约束优化
在科学计算中,优化是一个重要的任务,而 MATLAB 的 `fminunc` 函数可以用于无约束优化问题。
% 定义目标函数
fun = @(x) (x(1) - 3)^2 + (x(2) - 2)^2; % 目标函数
% 初始点
x0 = [0, 0];
% 调用优化函数
options = optimoptions('fminunc','Display','iter','Algorithm','quasi-newton');
[x, fval] = fminunc(fun, x0, options);
disp(['最优点: ', num2str(x)]);
disp(['最优值: ', num2str(fval)]);
总结
以上是一些使用 MATLAB 进行数据分析与科学计算的高效算法案例。这些例子展示了 MATLAB 强大的数学和统计功能,以及其在处理复杂计算和数据分析任务中的高效性。通过实践这些案例,程序员和研究人员可以更好地掌握 MATLAB 的应用,以提升自己的数据分析能力。
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
