题解：CF2150B Grid Counting

题解：CF2150B Grid Counting

思路

首先，因为题目的第二、三条限制，每个 $k$ 都对应一个黑色格子，所以黑色格子一共有 $n$ 个。

首先，我们必须在 $(1,1)$ 和 $(1,n)$ 位置放黑色格子，因为只有他们能满足 $k=1$ 时的第二、三条限制。

那么，在 $(1,1)$ 下面的格子就必须都为白色，因为 $(1,1)$ 对于第三条限制的 $k=n$，此时 $(1,1)$ 的 $n-y_i+1$ 为最大值，而在 $(1,1)$ 下面的点的的 $y_i=1$，和 $(1,1)$ 相等，所以不能选，以此类推，在 $(1,n)$ 下面的格子也必须为白色。

接下来考虑第二、三条限制 $k=2$ 的情况，因为第 $1$ 和 $n$ 列不能选，所以只能选第 $2$ 和 $n-1$ 列中 $x_i\ge 2$ 的格子。

以此类推，最终能选的格子即为下图：

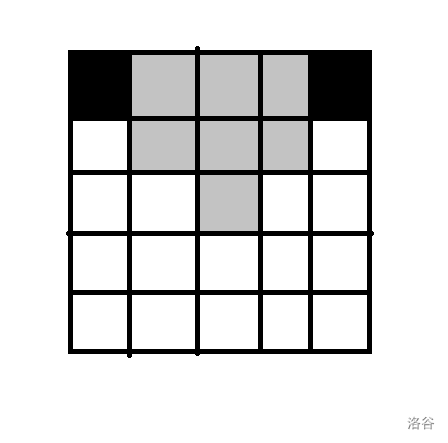
其中黑色为必选的部分，灰色为可选的部分（每列选一个）。

那么接下来我们倒序枚举 $n$ 到 $1$，设当前一共可以放的黑色格子数量为 $cnt$，每遇到可以放黑色格子的行就将 $cnt$ 加上本行加的黑色格子数量，比如到第 $2$ 行可以多放两个，如果 $cnt<a_i$ 则无解，每次将答案乘上 $\left(\genfrac{}{}{0ex}{}{cnt}{a_i}\right)$ 即可。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=998244353;
int t,n,a[200010];
ll f[200010];
ll qpow(ll a,ll b){ll ans=1;for(;b;b>>=1,a=a*a%mod)if(b&1)ans=ans*a%mod;return ans;
}
ll C(ll n,ll m){if(n<m)return 0;return f[n]*qpow(f[m],mod-2)%mod*qpow(f[n-m],mod-2)%mod;
}
int main(){ios::sync_with_stdio(0);cin.tie(0);f[0]=1;for(int i=1;i<=200000;i++)f[i]=f[i-1]*i%mod;cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}int cnt=0,fl=1;ll ans=1;for(int i=n;i>=1;i--){if(i*2==n+1)cnt++;else if(i*2<=n)cnt+=2;if(cnt<a[i]){fl=0;break;}ans=ans*C(cnt,a[i])%mod;cnt-=a[i];}if(cnt!=0||!fl){cout<<"0\n";}else{cout<<ans<<'\n';}}return 0;
}