当前位置：首页 > news >正文

迪杰斯特拉（dijkstra）算法

news 2025/10/30 14:47:23

在讲代码以前，先了解dijkstra算法的思想以及注意事项：

核心思想

算法的核心思想是贪心算法。它通过逐步确定从源点到图中其他所有顶点的最短路径。

1.将顶点集合分为两组：

a. 已确定最短路径的顶点集合（U）：初始时，这个集合只包含源点本身。

b. 未确定最短路径的顶点集合（V）：初始时，包含除源点外的所有顶点。

2. 从集合 V 中选出当前“距离”源点最近的顶点，将其加入集合 U。

3. 更新集合V中，这个新加入顶点的所有邻居到源点的“当前最短距离估计值”。这个过程称为“松弛”操作。

4. 重复步骤 2 和 3，直到所有顶点都包含在集合 U 中，即找到了源点到所有顶点的最短路径。

重要前提

非负权边：迪杰斯特拉算法要求图中所有边的权值都为非负数（例如，不能有负数距离或成本）。如果存在负权边，算法可能无法得出正确结果。
单源：它计算的是从一个固定的源点出发到所有其他点的最短路径。

步骤解析

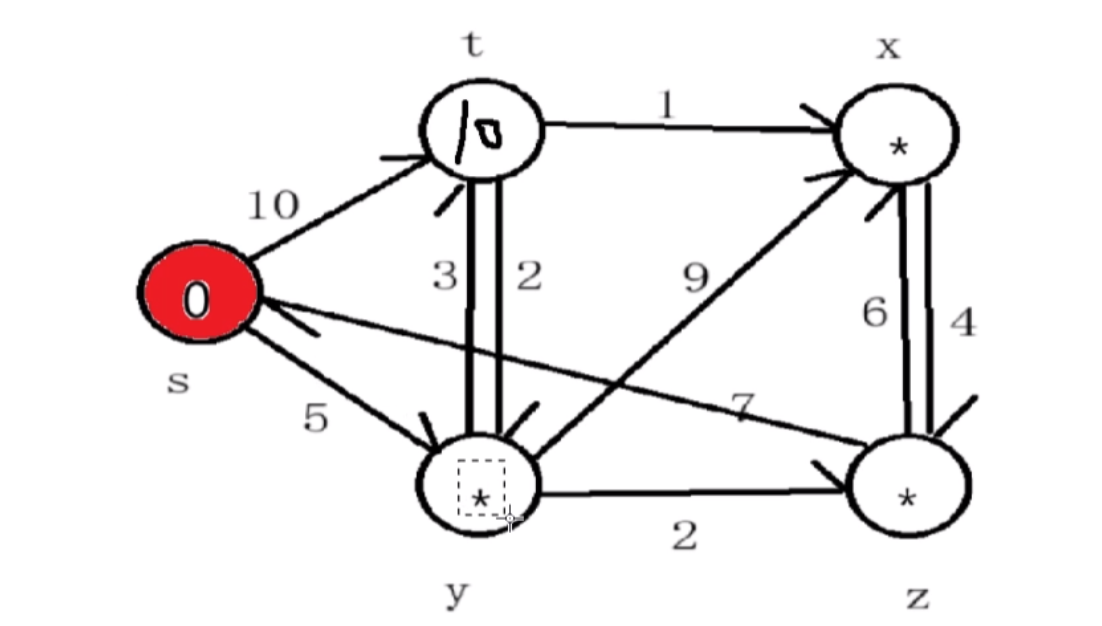
以上图为例，先定义顶点s作为起始点，此时更新能够到达的边距离(这里INT_MAX表示无穷大)：

s->y:5 s->t:10 s->z:INT_MAX s->x:INT_MAX

这里我们要注意，dijkstra算法是只适用于负权值的有向网

在将起始点加入以后，肯定会选择一条相邻的最短路径边进入已确定最短路径的顶点集合U，每添加一个顶点到U集合以后，更新源点到V集合（未确定最短路径的顶点集合）中的各顶点的最短路径估计值

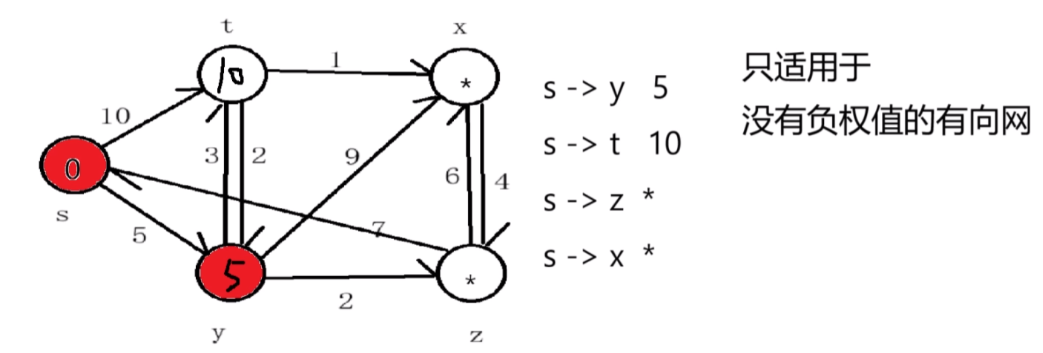
将y添加到集合U中，更新到V集合中的点，此时可以到达的顶点t更新为8(5+3)、顶点z更新为7(5+2)、顶点x更新为14(5+9)，

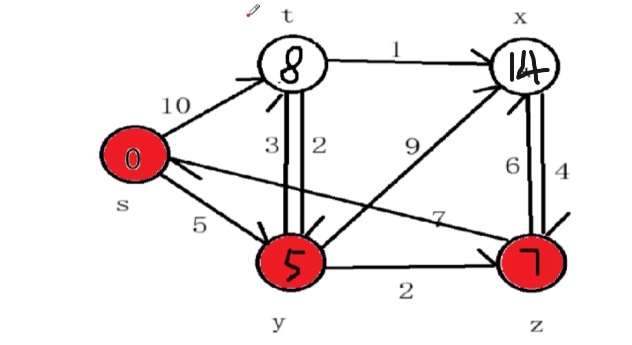
选择V集合中最短一条边添加对应顶点到U集合后，更新V集合；这里将z添加到U集合后，从源点s顶点x的距离现在为13(5+2+6)比原来的14(5+9)小，更新集合V中顶点x的数据。

然后重复2、3步骤，选择集合V中的最短一条边，添加对应点t到集合U，更新集合V，从源点s到x的距离可以为9(5+3+1)比上一次更新后集合V中的距离13(5+2+6)更小，那么更新集合V中x的数据

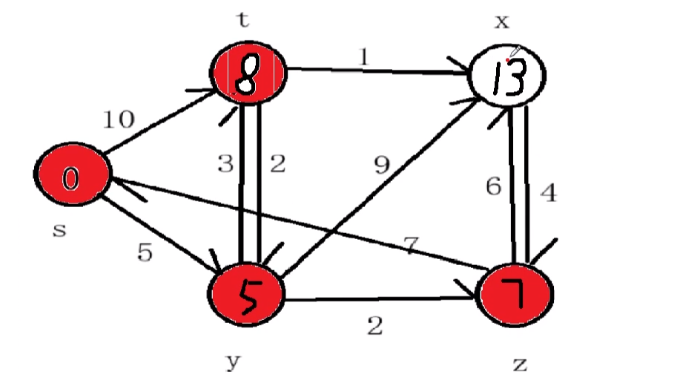
最后所有顶点均被添加至集合U中，集合U中所存数据即为最短路径。

代码准备

判断顶点是否已被添加至集合U：和之前Prim算法思路类似，定义一个bool类型的数组，名为sptset，初值为false，每添加一个，就更新对应顶点下标的sptset数组元素为true，表示已经添加到集合U；定义一个名为parent的数组，记录当前下标对应的顶点，它的父顶点，比如

下标2对应的是顶点表中下标为2的元素，下标为1对应的是顶点表中下标为1的元素，只不过parent类型的值存的是它父节点的下标，也就是说parent的父节点是下标1对应的元素……

dist数组：存储集合V的数据，更新源点到各个顶点之间的距离估计

代码

先用for循环对g->vertexNum个顶点的对应下标数组初始化，然后源点(起点距离初始化为0)

void Dijkstra(Graph* g,int src) {bool* sptSet = malloc(sizeof(bool) * g->vertexNum);int* parent = malloc(sizeof(int) * g->vertexNum);//类似集合vint* dist = malloc(sizeof(int) * g->vertexNum);for (int i = 0; i < g->vertexNum; i++) {sptSet[i] = false;parent[i] = -1;//表示没有父亲，也可以初始化为i，自己是自己的下标dist[i] = INT_MAX;}dist[src] = 0;

用两段for循环模拟步骤二、三：

第一层for循环是在集合v中寻找最短路径，添加到集合U(sptSet数组)中，设置对应下标元素为true,表示已经添加，第二段代码进行松弛操作，将符合要求的顶点更新：顶点不在集合U中，顶点v到顶点j之间存在一条有向路径（因为添加到集合U中的一个顶点对应下标为v，如果v和下标j之间有一条路径，进行第三条判断），最短路径（源点->下标v顶点）+ 下标v顶点->下标j顶点距离之和小于源点直接->下标j顶点的距离，就更新集合V，（因为下次还从集合V中选）

//松弛操作
for (int i = 0; i < g->vertexNum - 1; i++) {//从集合V的顶点中，找一个离源点最近的顶点加入U集合中int v = minDistance(dist, sptSet,g->vertexNum-1);//添加这个顶点到U集合中sptSet[v] = true;//松弛操作//已经加入到U集合的顶点就不用再做松弛操作，因为他们一定是各自到源点的最短距离for (int j = 0; j < g->vertexNum; j++) {//先判断要访问的顶点是否已经加入U集合//顶点下标v到j必须有值，两点之间必须存在路径才行//如果源点到v，加上v到j的距离小于源点到j的距离，将集合v更新；if (!sptSet[j] && g->edge[v][j]!=INT_MAX && dist[j] > dist[v] + g->edge[v][j]) {dist[j] = dist[v] + g->edge[v][j];parent[j] = v;//记录源点到 [下标j顶点] 的路径，记录[下标j顶点]的父亲节点}}
}

大致完整代码：

int minDistance(int* dist, bool* sptSet,int n) {int min = INT_MAX;int minPos = -1;for (int i = 0; i < n; i++) {if (!sptSet[i] && dist[i] < min) {//false取反为truemin = dist[i];minPos = i;}}//for循环寻找距离源点最短的顶点//返回最短路径对应顶点下标return minPos;
}void printPath(int* parent, int v) {if (parent[v] == -1) {printf("%d", v);return;}printPath(parent, parent[v]);printf("->%d", v);
}void Print(int* parent, int* dist, int src, int n) {printf("源点%d到各个顶点的最短路径：\n", src);printf("目标顶点\t最短距离\t路径\n");for (int i = 0; i < n; i++) {if (src != i) {printf("%d\t\t%d\t\t", i, dist[i]);printPath(parent, i);printf("\n");}}
}/// <summary>
/// 迪杰斯特拉算法
/// </summary>
/// <param name="g">邻接表</param>
/// <param name="src">源点下标</param>
void Dijkstra(Graph* g,int src) {bool* sptSet = malloc(sizeof(bool) * g->vertexNum);int* parent = malloc(sizeof(int) * g->vertexNum);//类似集合vint* dist = malloc(sizeof(int) * g->vertexNum);for (int i = 0; i < g->vertexNum; i++) {sptSet[i] = false;parent[i] = -1;//表示没有父亲，也可以初始化为i，自己是自己的下标dist[i] = INT_MAX;}dist[src] = 0;//松弛操作for (int i = 0; i < g->vertexNum - 1; i++) {//从集合V的顶点中，找一个离源点最近的顶点加入U集合中int v = minDistance(dist, sptSet,g->vertexNum-1);//添加这个顶点到U集合中sptSet[v] = true;//松弛操作//已经加入到U集合的顶点就不用再做松弛操作，因为他们一定是各自到源点的最短距离for (int j = 0; j < g->vertexNum; j++) {//先判断要访问的顶点是否已经加入U集合//顶点下标v到j必须有值，两点之间必须存在路径才行//如果源点到v，加上v到j的距离小于源点到j的距离，将集合v更新；if (!sptSet[j] && g->edge[v][j]!=INT_MAX && dist[j] > dist[v] + g->edge[v][j]) {dist[j] = dist[v] + g->edge[v][j];parent[j] = v;//记录源点到 [下标j顶点] 的路径，记录[下标j顶点]的父亲节点}}}//打印parent数组即为顶点相连顺序；Print(parent, dist, src,g->vertexNum);
}

主函数：

int main()
{vertexType arr[] = { 's','y','z','t','x' };Graph g;initGraph(&g, arr, 5, 10);addEdge(&g, 's', 't', 10);addEdge(&g, 's', 'y', 5);addEdge(&g, 'y', 't', 3);addEdge(&g, 'y', 'z', 2);addEdge(&g, 'y', 'x', 9);addEdge(&g, 'z', 'x', 6);addEdge(&g, 'z', 's', 7);addEdge(&g, 't', 'y', 2);addEdge(&g, 't', 'x', 1);addEdge(&g, 'x', 'z', 4);printGraph(&g);//DFS(&g);putchar('\n');//BFS(&g);//minSpanTree_Prim(&g);Dijkstra(&g, 0);return 0;
}

最终结果：