《考研408数据结构》第六章(5.4树和森林)复习笔记
一、树的存储结构
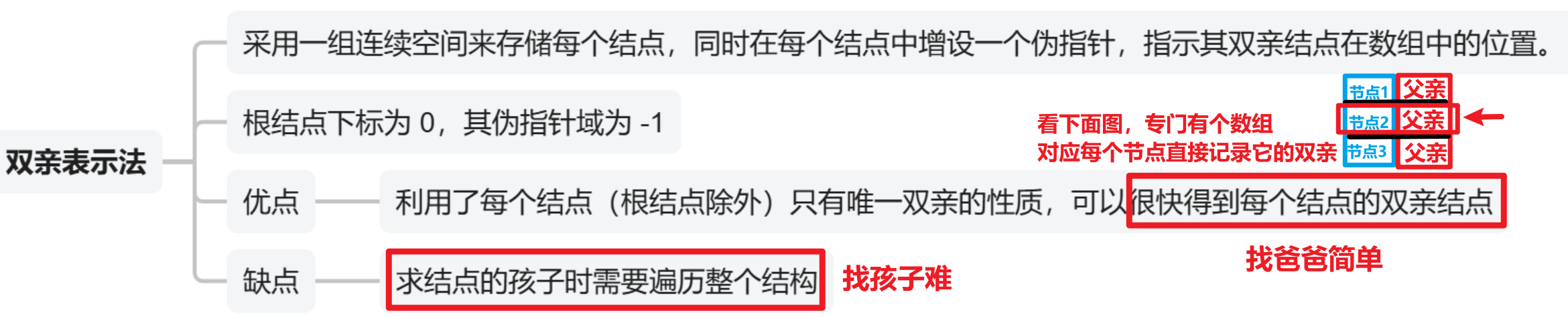
1、【双亲表示法】:孩子找爸爸
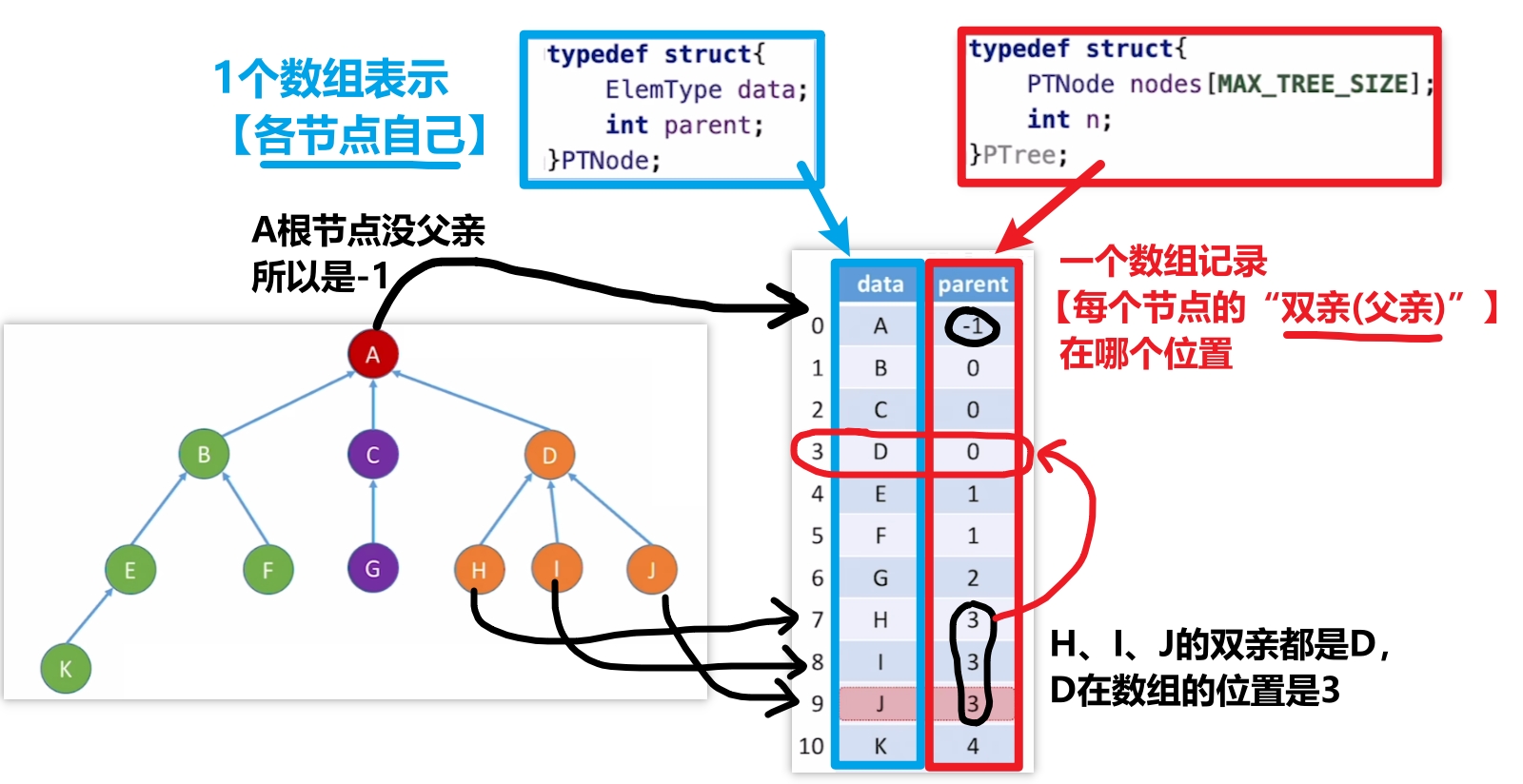
- 1、是【顺序存储】,你就记住两数组就行了
- 2、各个节点带着【自己双亲】
- 3、找孩子节点麻烦,要遍历;找父亲节点方便!
- 解释:首先我们要知道【数组】是可以根据 a[i] 一步定位的
- 【找父亲】是知道孩子在【节点数组的:a[i]】了,一步定位到孩子,然后找到孩子指向的双亲
- 【找孩子】是虽然知道父亲在【节点数组的:a[i]】,但是它只记录着自己的父亲
- 它的孩子节点还是要遍历整个【节点数组】,并一一对比每个节点的父亲是不是自己
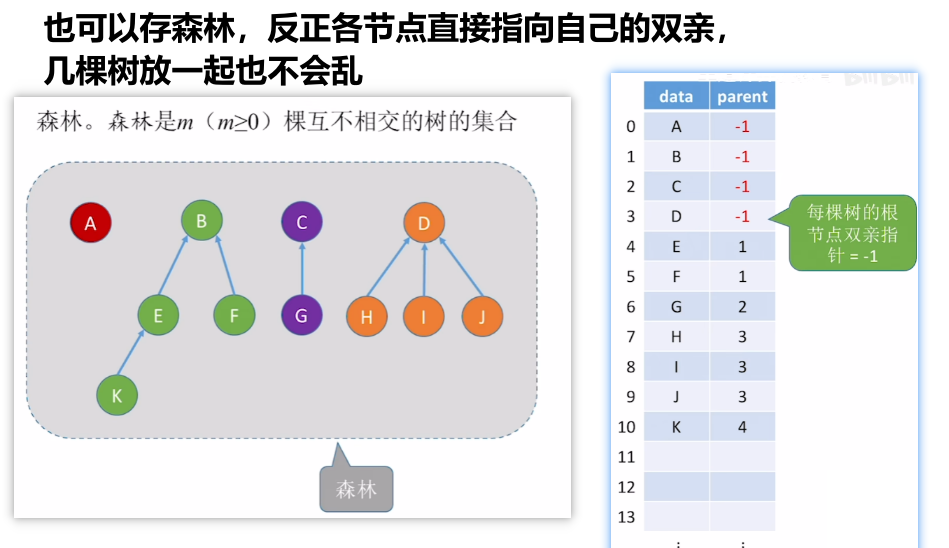
- 3、记录森林也方便,就是几个树都放同数组里,各节点指向自己的根就行了
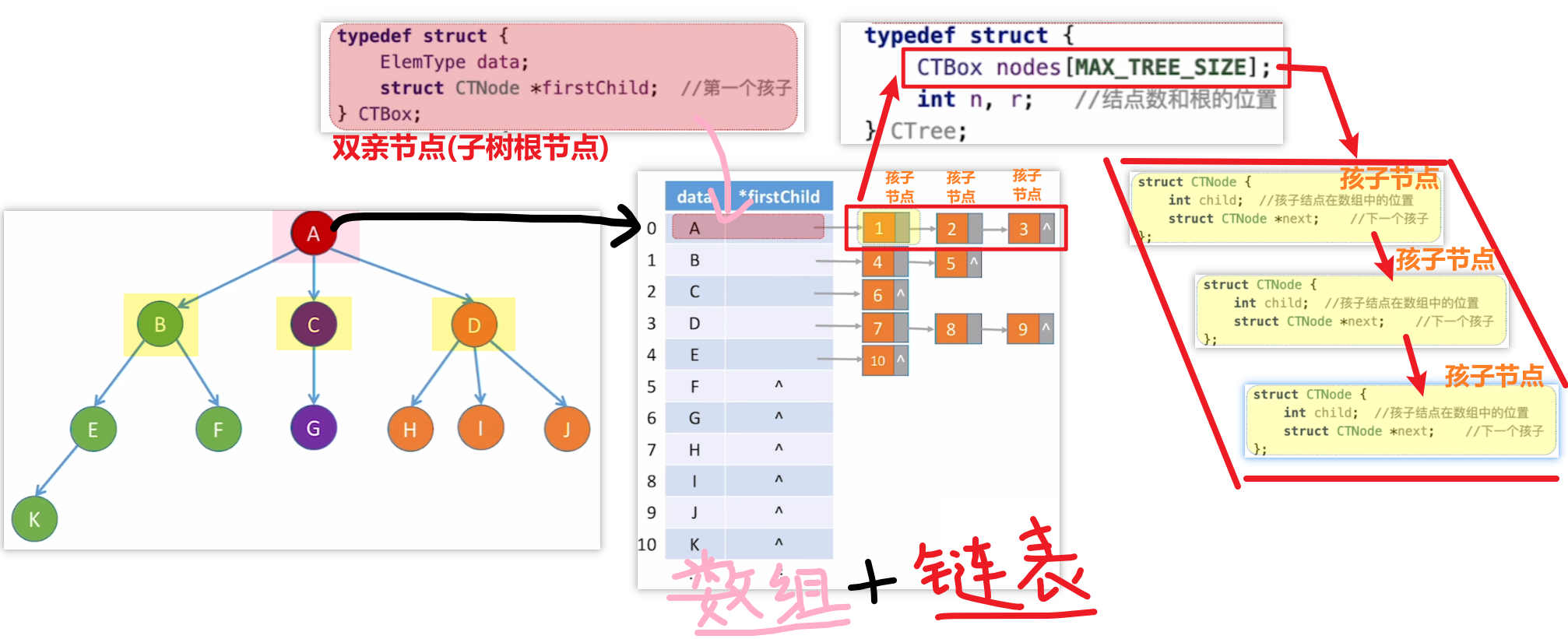
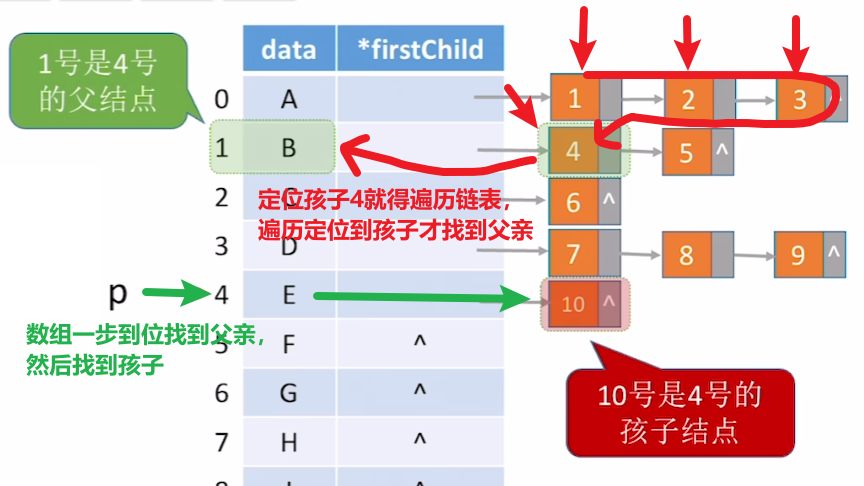
2、【孩子表示法】:爸爸带孩子
- 1、是【顺序存储】+【链式存储】
- 你就记住【数组:存双亲节点】、【链表:记录每个节点的孩子节点】
- 2、找父亲节点麻烦,要遍历链表;找孩子节点方便!
- 解释:
- 【找孩子】是知道父亲在【节点数组的:a[i]】了,一步定位到父亲,然后找到它的孩子
- 【找父亲】是先遍历【节点数组的:a[i]】、再遍历这些父节点的【孩子链表】
- 一一对比每个节点的孩子是不是自己,是的话才找到父亲
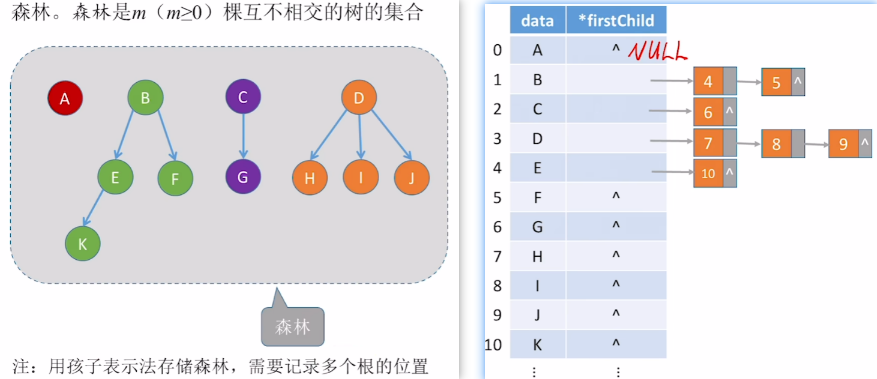
- 3、也可以存森林
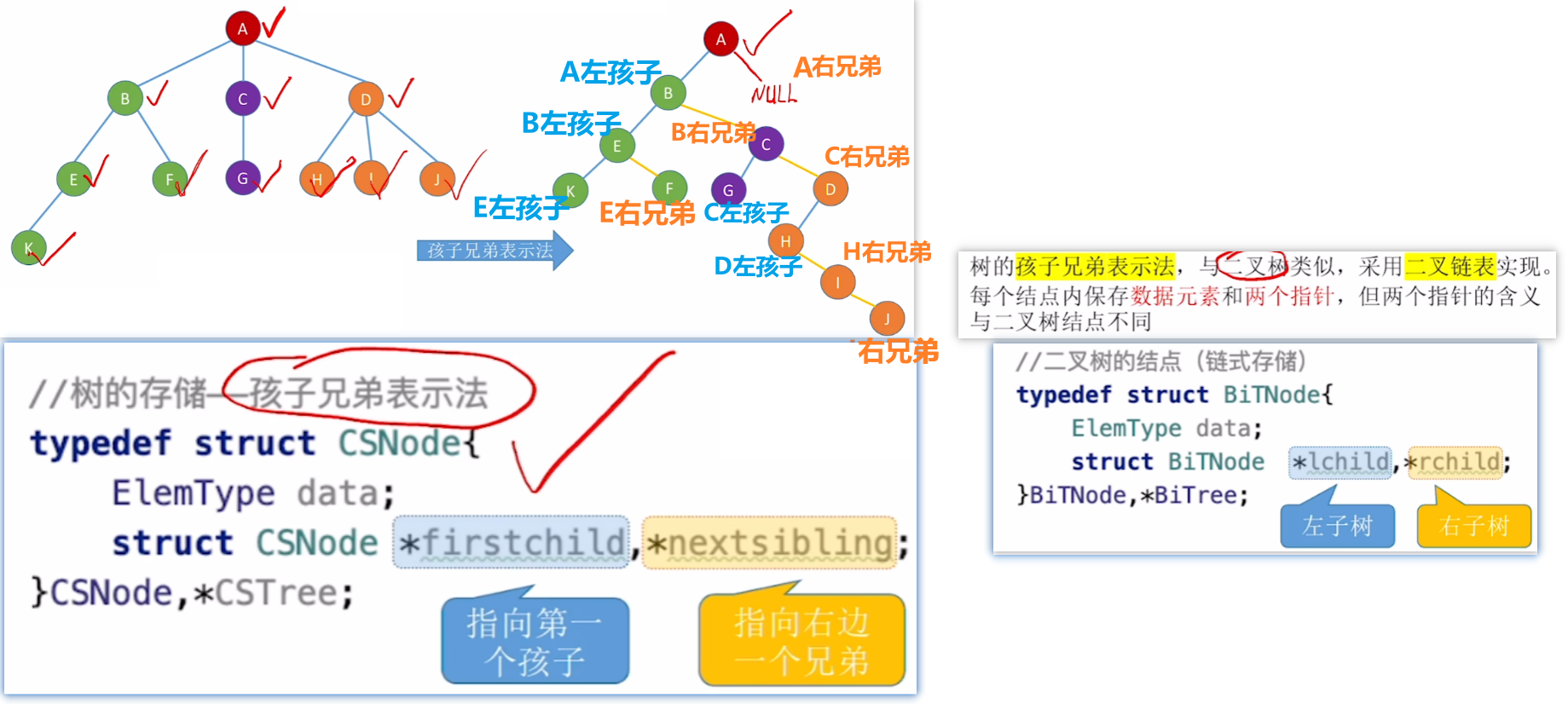
3、【孩子兄弟表示法】:记录左孩子 + 右兄弟
- 1、每个节点的数据结构类似二叉树:
- 都有2各指针,只不过【孩子表示法】的指针意义是:
- 【左指针】:指向自己的第一个孩子(多个孩子情况只记录最左边的)
- 【右指针】:指向自己的右边的兄弟节点
- 从而让【树】变成【二叉树】
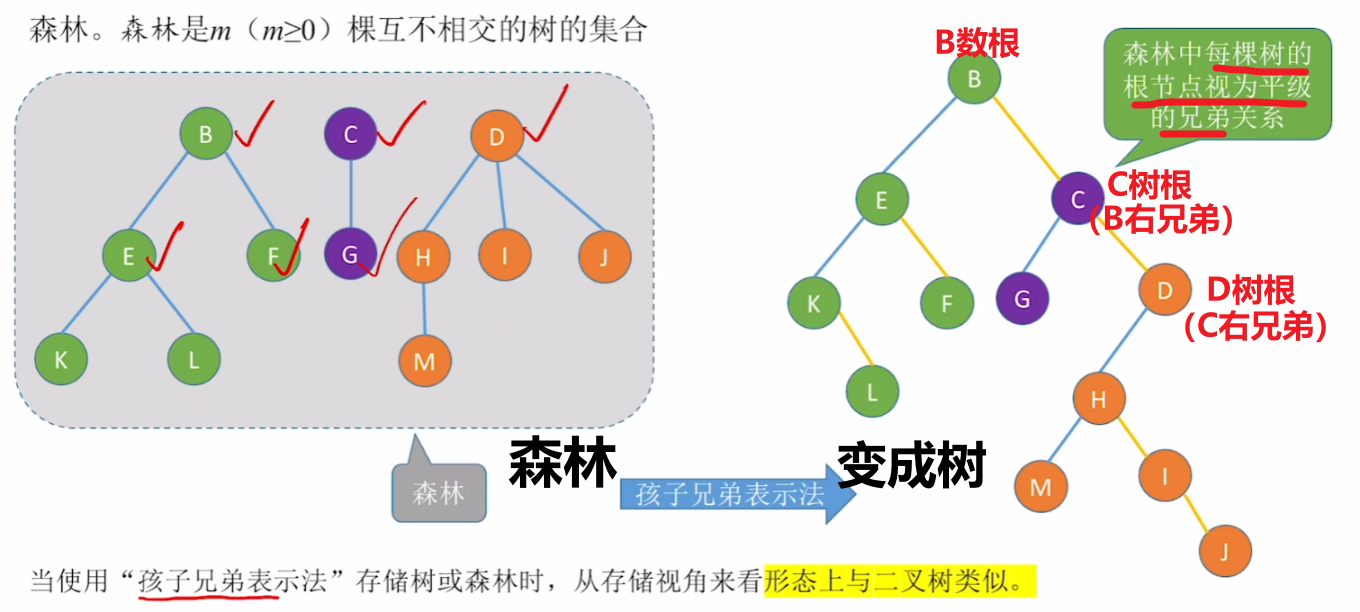
- 2、也可以表示森林:
- 不过把【森林】里各个树,合成了一整个【二叉树】
- 各个【树的根】是平级的【兄弟关系】
二、树、森林、二叉树转换
前面树的存储结构,我们学了只有【孩子兄弟表示法】可以把【树—>二叉树】、【森林—>二叉树】,所以下面我们用的方法还是【孩子兄弟表示法】
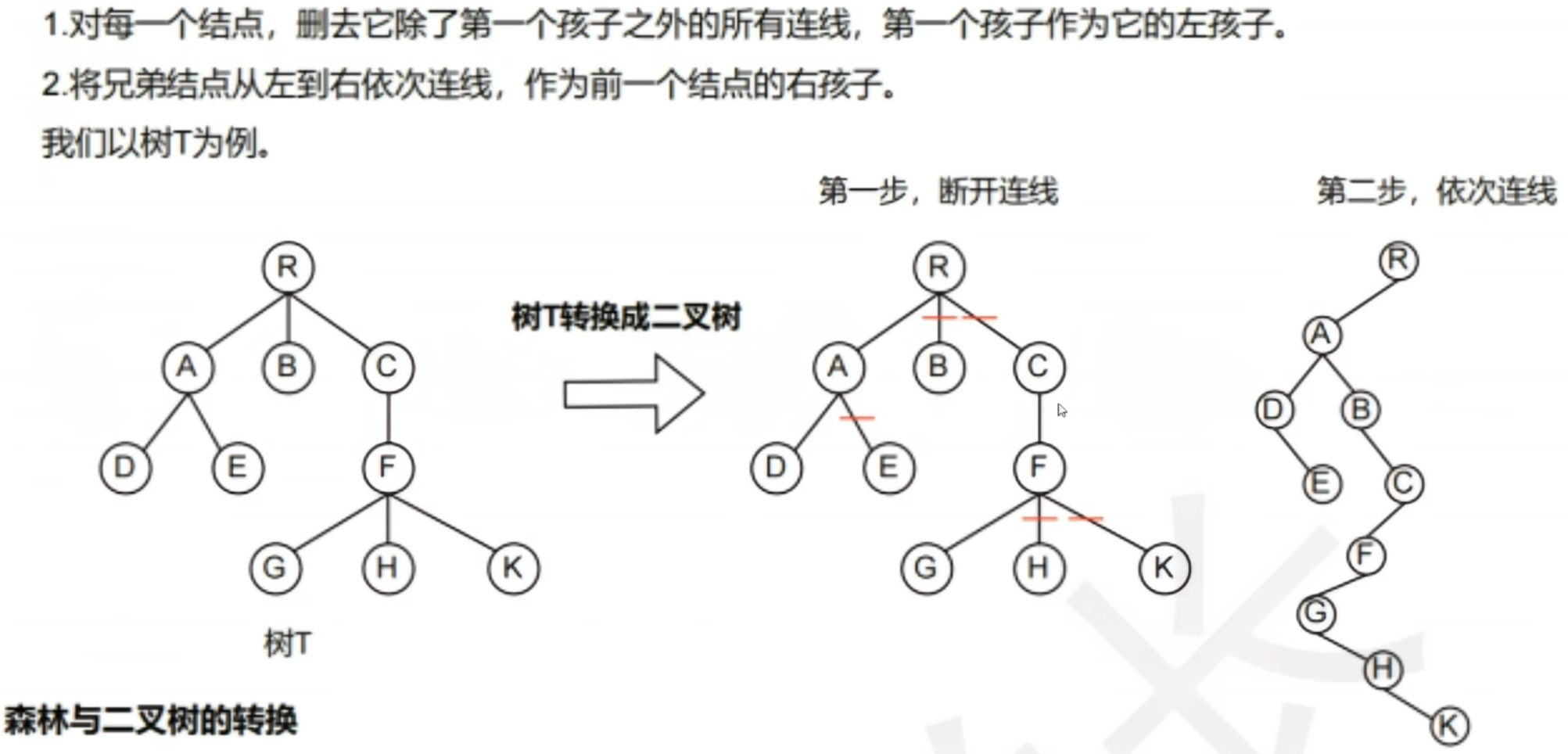
1、【树—>二叉树】
- 做题画变化的【技巧】:
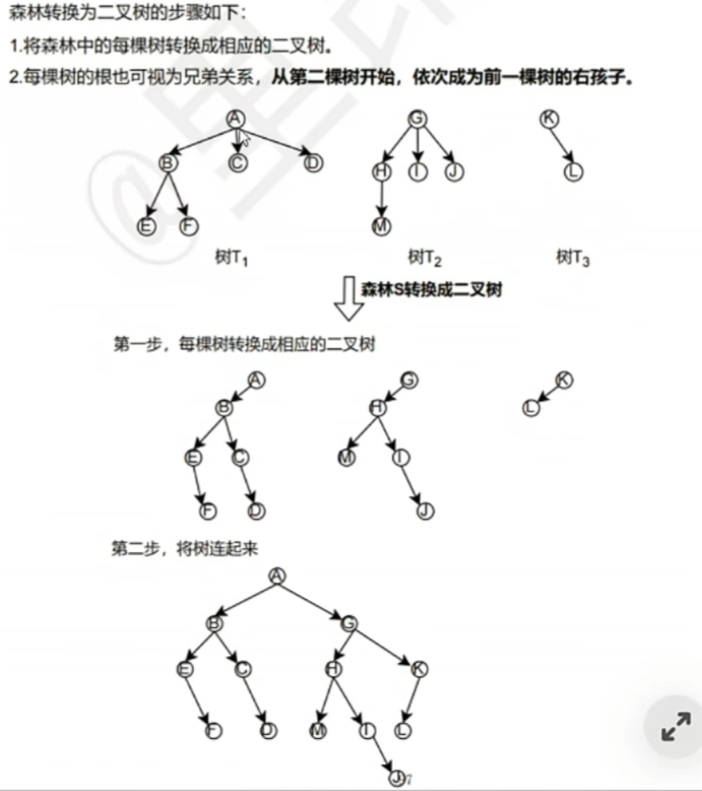
2、【森林—>二叉树】
- 做题画变化的【技巧】
- 先生成对应的【孩子表示法】的二叉树,再把树连起来
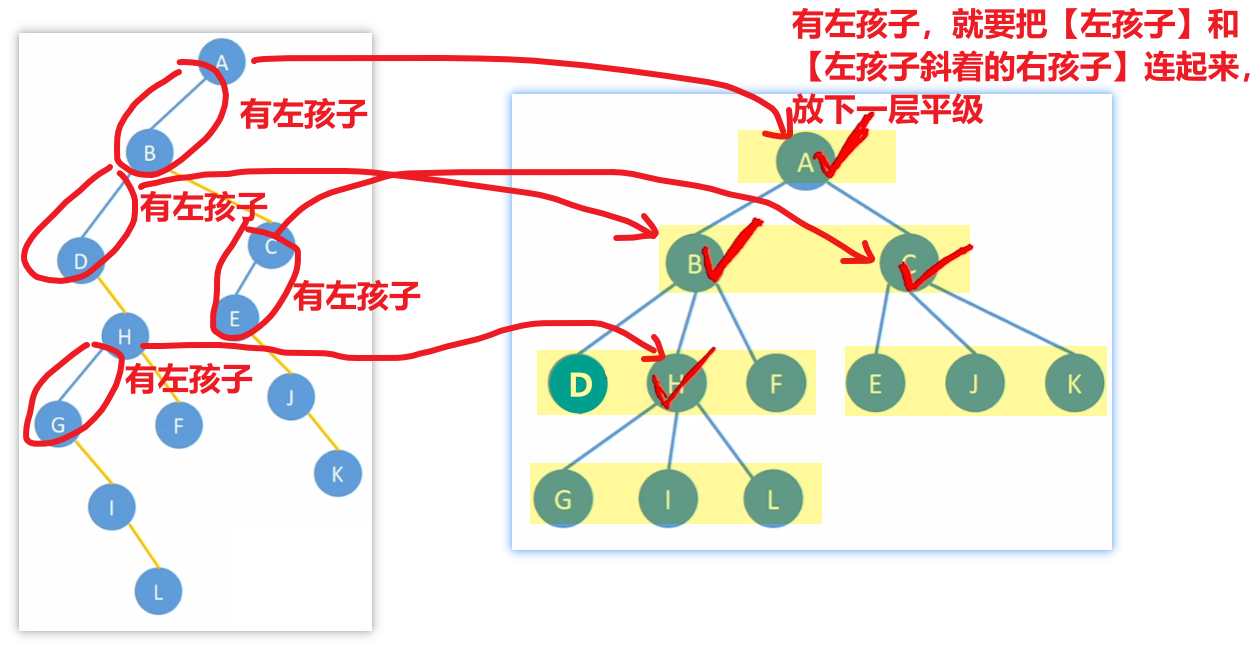
3、【二叉树—>树】
- 做题画变化的【技巧】
- 看图吧,没什么好说的
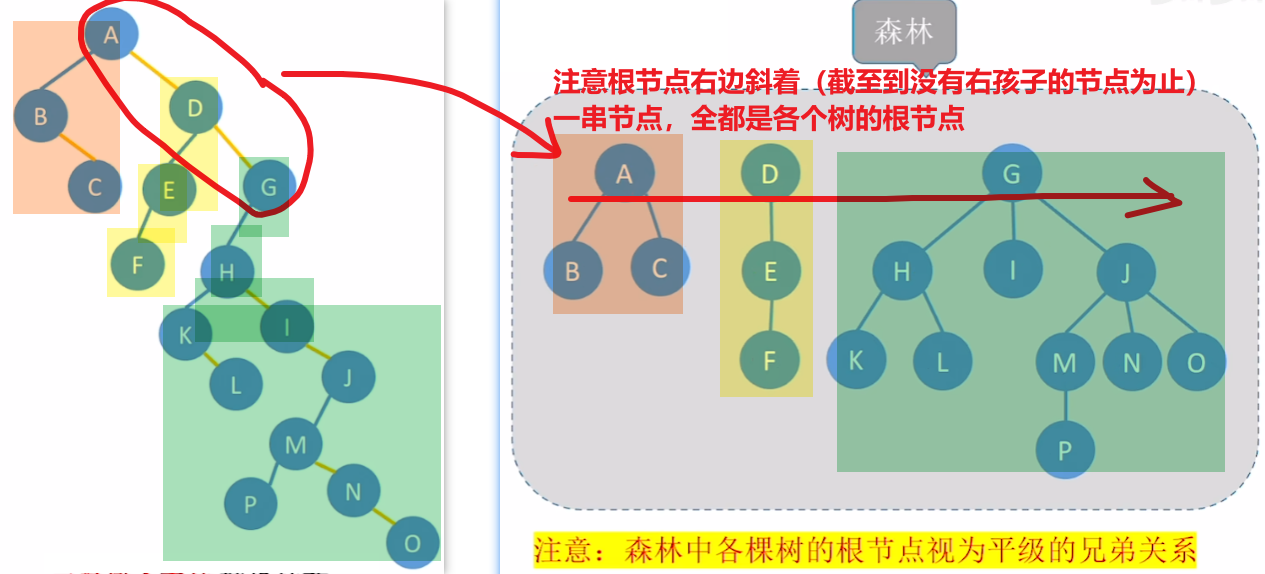
4、【二叉树—>森林】
- 做题画变化的【技巧】
- 看图吧,没什么好说的,我刚学没听他讲都知道怎么画了,自己动一下手的事
三、树和森林的遍历
其实学过二叉树的遍历,这里就巨鸡儿简单
1、树的遍历
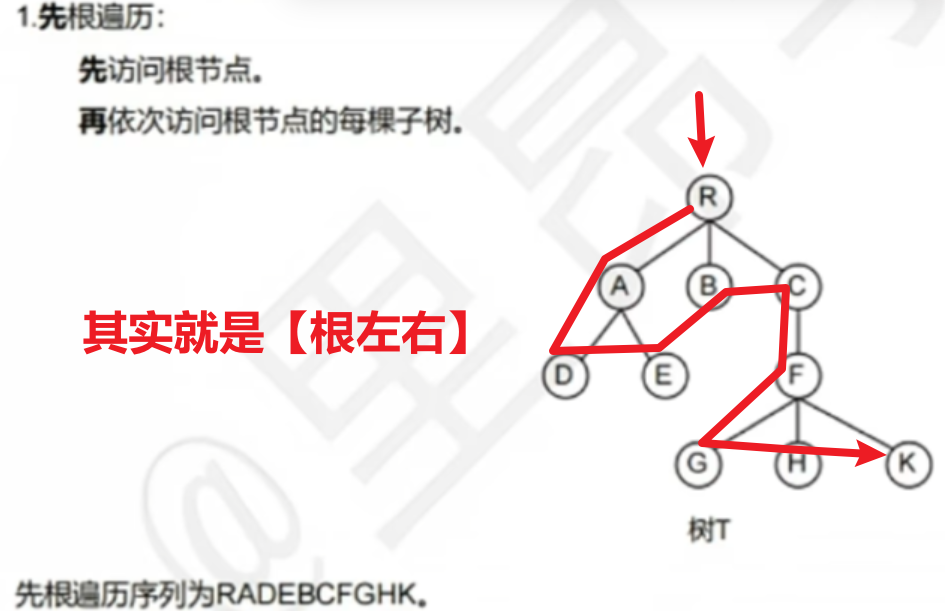
【先根遍历】
- ① 你其实按二叉树的规则自己从【根 左—>右】的顺序,也能写出结果
- 【依我个人感觉,这样直接念出来更方便】
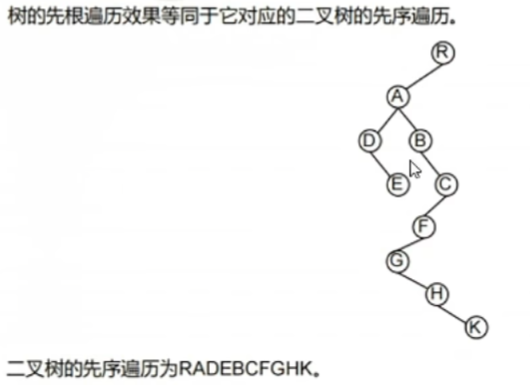
- ② 你要非看不懂,那就老实把树换成【孩子兄弟表示法:二叉树】
- 再【根左右】,结果也是一样的
;
;
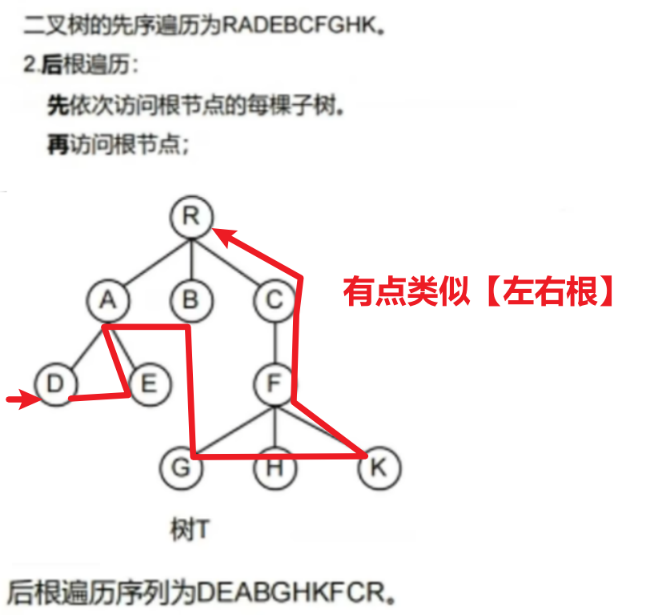
【后根遍历】
- ① 你其实按二叉树的规则自己从【后序遍历:左—>右 根】的顺序,也能写出结果
- 【依我个人感觉,这样直接念出来更方便】
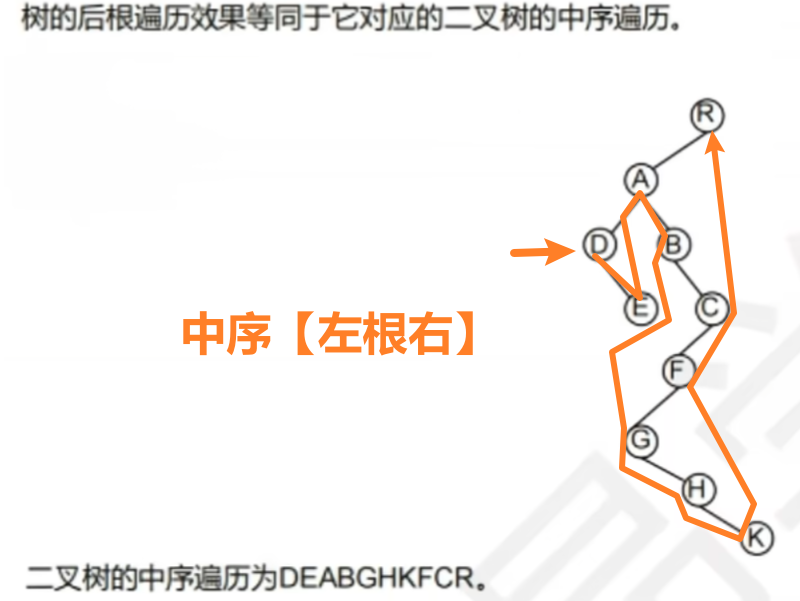
- ② 你要非看不懂,那就老实把树换成【孩子兄弟表示法:二叉树】
- 不过二叉树形式就要用【中序遍历:左根右】了
;
;
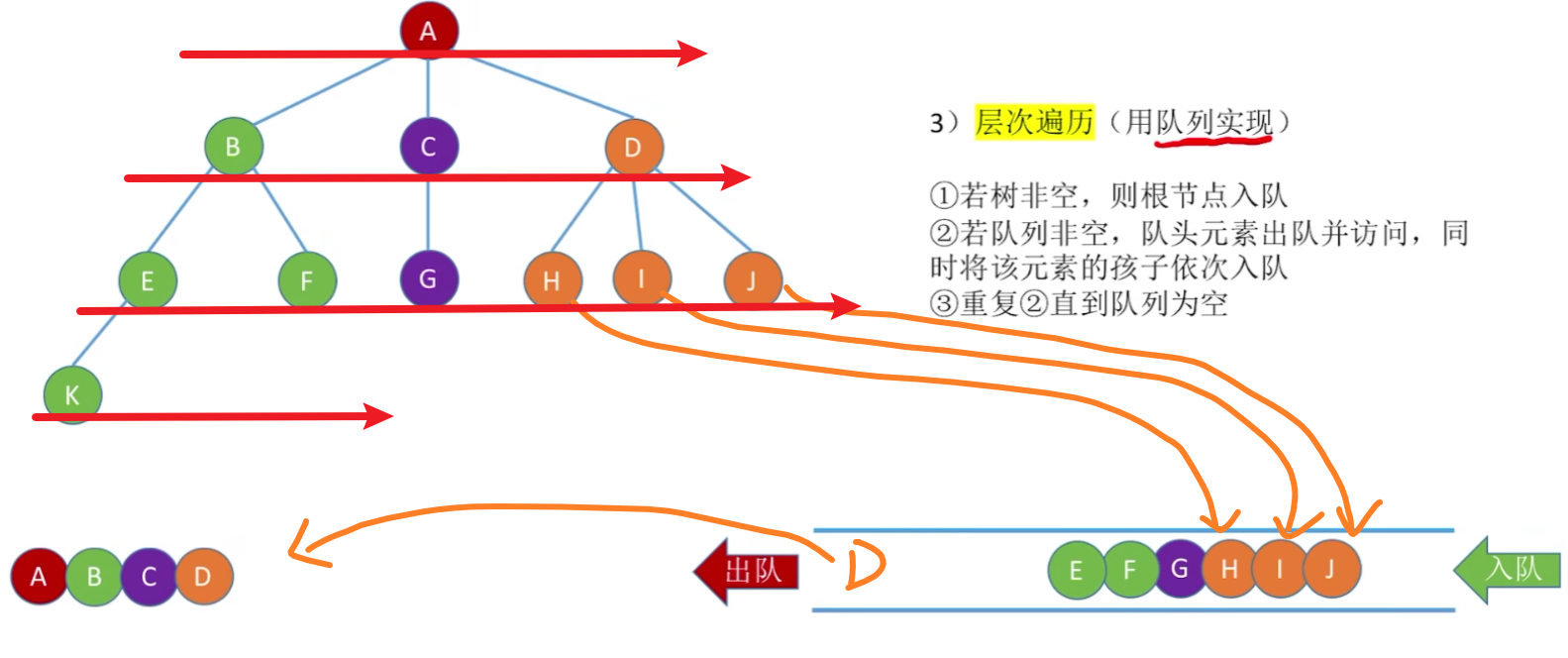
- 【层次遍历】
- 更没什么可说的,根二叉树压根一丁点区别都没有,完完全全一模一样!
2、森林遍历
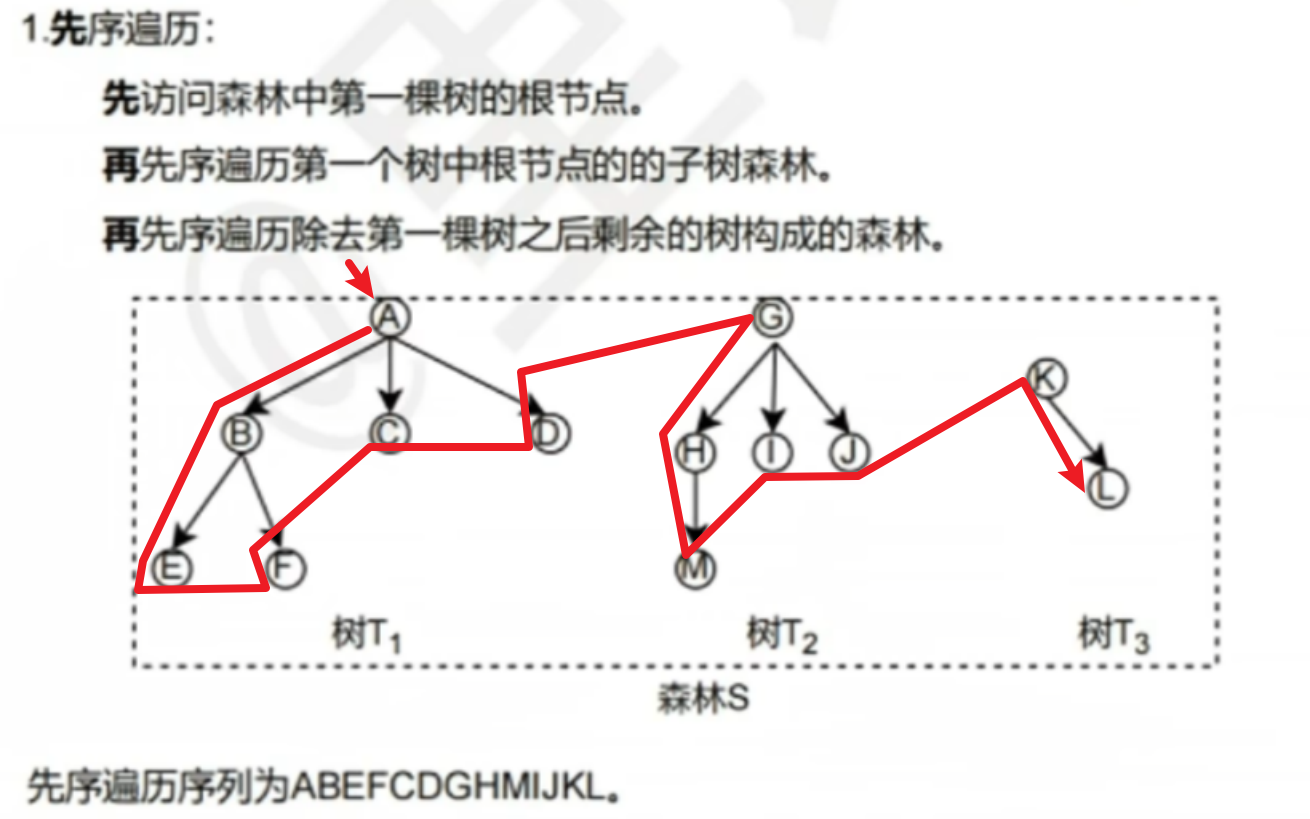
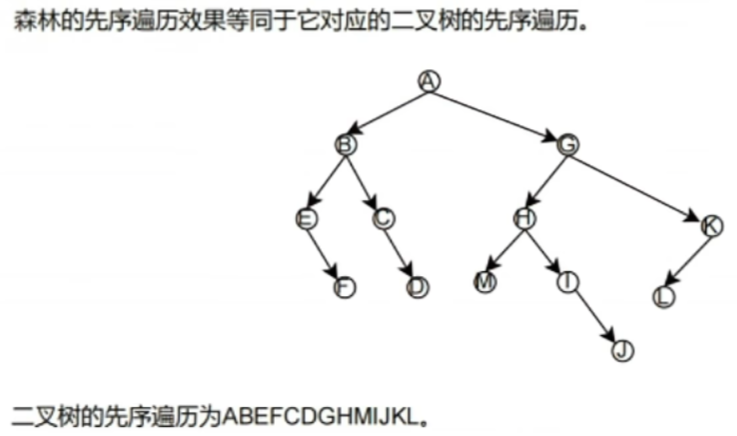
【先序遍历】
- ① 就只是先遍历第一棵树、再遍历第二棵树......就这么弱智的知识点
- ② 你要真的很闲,那就画成【二叉树】再遍历,你喜欢就好
;
;
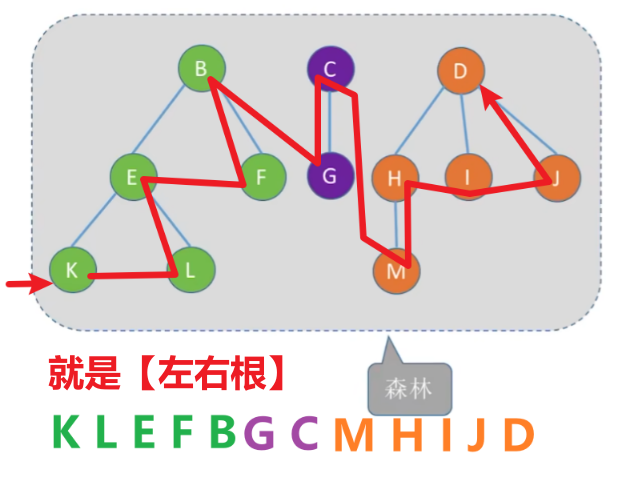
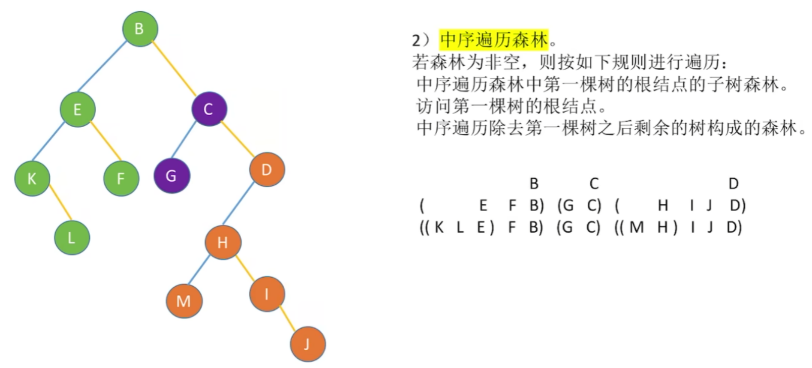
【中序遍历】
- ① 就是分别从第一颗到最后一棵树,按【后序遍历:左—>右 根】来
- ② 还是那句话,你很闲就画成【二叉树】再【中序遍历】