机器学习日报07

摘要

今天的学习让我对机器学习中的学习曲线有了更深入的理解。通过学习曲线，我能够直观地看到训练误差和验证误差随训练集大小变化的关系，这帮助我更好地诊断模型是否存在高偏差或高方差问题。当模型出现高偏差时，增加数据量效果有限，需要增加特征或使用更复杂模型；而高方差时，增加数据量通常能显著提升性能。最后，我还学习了神经网络如何通过调整规模来平衡偏差和方差，以及如何在代码中实现L2正则化来防止过拟合。

Abstract

Today’s study focused on learning curves in machine learning and their role in diagnosing bias and variance issues. I learned to analyze how training error and cross-validation error change with training set size, identifying high bias (where both errors remain high) and high variance (where there’s a large gap between errors). For neural networks, increasing network size helps reduce bias, while adding more data addresses variance. I also implemented L2 regularization in code using kernel_regularizer=L2(0.01) to prevent overfitting in larger networks.

一、学习曲线

学习曲线可以帮助我们理解学习算法在不同数据量下的表现

让我们绘制一条拟合二次多项式函数模型的学习曲线，我会绘制Jcv、交叉验证误差，以及Jtrain训练误差，在这张图上，横轴表示m，即训练集的大小，或者是算法可以学习的示例数量，纵轴是误差，即Jcv或Jtrain，它看起来是这样的

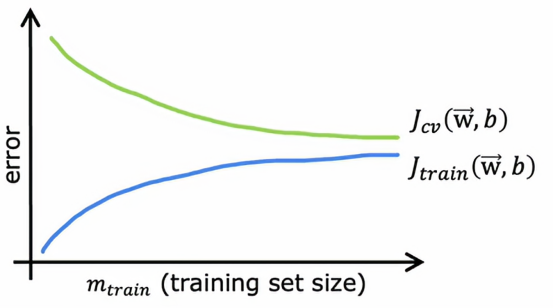
Jcv随着训练集大小变大而变小，Jtrain随着训练集大小变大而变大

我们从只有一个训练样本的例子开始，如果我们用二次模型来拟合这个数据，我们可以轻松拟合一条直线或曲线，你的训练误差将为0

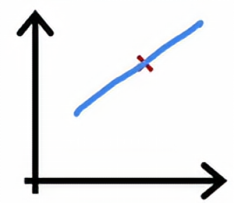
当有两个训练样本的时候，我们可以再次拟合一条直线，并实现零训练误差，事实上，如果我们有三个训练样本，二次函数依然可以很好地拟合，并几乎达到零训练误差


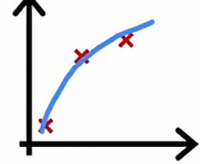
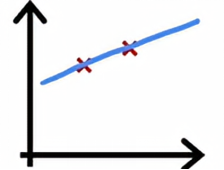
当我们有四个样本的时候，要完美拟合这四个样本会稍微有点困难一些，我们可能会得到一个看起来像这样的曲线，总体拟合得不错，但在某些地方稍微有点误差。

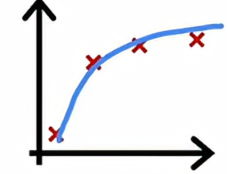
当我们有五个训练误差时候，我们仍然可以适当拟合，但要完美拟合所有样本会更难一点。

所以当我们逐步增大训练集，要完美拟合每一个训练样本将会变得越来越困难，交叉验证误差通常会比训练误差更高，因为我们是对训练集拟合参数，因此肯定是期望在训练集上至少有一点点更好，或者当m很小得时候，甚至可能在训练集上比交叉验证集好很多。

现在让我们看看高偏差与高方差的学习曲线是什么样子，我们先从高偏差或欠拟合的情况开始，回想高偏差的例子，是用线性函数拟合了一个看起来像这样的函数

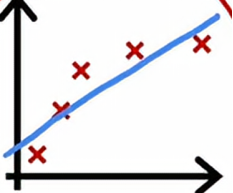
如果我们要绘制训练误差，那么训练误差将会像这样上升，就像我们预期的那样，事实上，这条训练误差曲线可能会开始变平，我们称之为平台，这意味着经过一段时间会变平，这是因为当我们获得越来越多的训练样本时，在拟合简单的线性函数时，我们的模型实际上不会发生太大的变化，它是在拟合一条直线，即使你获得更多更多样本，没有太多可以改变的，这就是为什么平均训练误差在一段时间后会趋平，同样的，我们的交叉验证误差会下降，而且经过一段时间后会趋平，这就是为什么Jcv再次要高于Jtrain，因为我们即使获得越来越多的样本，我们拟合的直线不会有太多改变，这个模型太简单不适合那么多的数据，这就是为什么这两个曲线Jcv和Jtrain会在一段时间后趋平

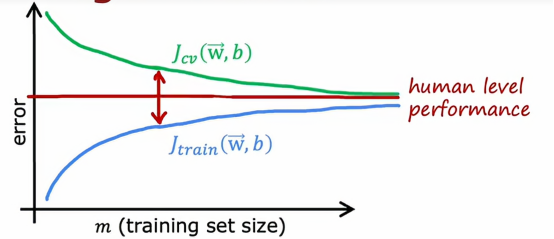
如果我们有一个基准性能的衡量标准，比如人的水平表现

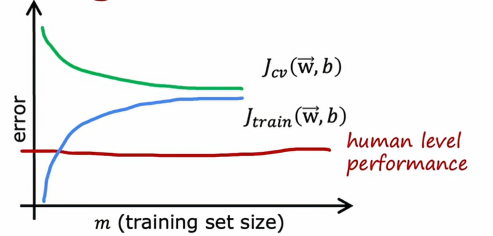
那么它的值可能会低于我们的Jtrain和Jcv，所以人的水平表现可能是这样的，基准性能和Jtrain之间有一个很大的差距，这是我们判断这个算法具有高偏差的指标，也就是说，如果我们能够拟合一个比直线更复杂的函数，预期会有更好的表现

那么现在如果我们延长x轴，也就是增大训练集的大小，Jcv和Jtrain始终会保持这个近似于水平的样子，所以这就得出一个结论，如果一个学习算法有高偏差，增加太多的数据本身页帮不了什么忙，我们的固有思维都是认为，只要我们的数据足够的多，算法的表现就会越好，但如果我们的算法有高偏差，那么我们只是增加更多的训练数据，也不会降低错误率很多，这就是问题所在，无论再添加多少示例，简单的线性组合也不会有太大的改善，这就是为什么在投入大量精力收集更多的训练数据之前，我们得检查我们的学习算法是否有高偏差

让我们看看高方差的学习算法曲线长什么样

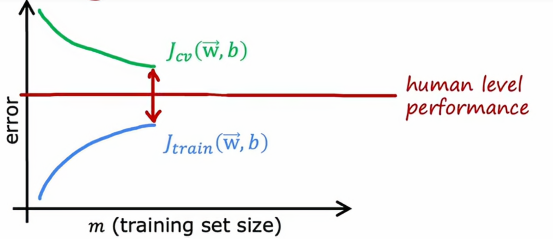
由上图可以看出，它在训练集上的表现远好于交叉验证集上的表现，如果我们绘制一个基准性能水平，它会出现在这里，这就表明，Jtrain有时候可能高于人类水平表现，我们可能对训练集拟合的非常好，从而使误差低得不切实际，例如在这个例子里误差为0

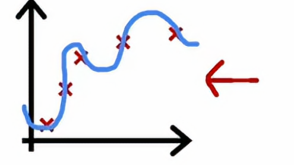
这实际上比人类预测房价得能力还要好，但同样，高方差得信号使Jcv是否远高于Jtrain，当我们有高方差时，增加训练集得大小可能会有很大得帮助，比如我们将图像往右推，会得到这样得图像

这样只需增加训练集得大小就可以降低交叉验证误差，使我们得算法性能越来越好

二、再次决定下一步做什么

专业程序员会经常查看训练误差和交叉验证误差，以判断算法是否具有高偏差或高方差，事实证明，这将帮助我们做出更好得决定，知道下一步该干什么，以提高我们算法的性能，

我们来看一个例子，当我们的算法出现高偏差的时候，我们一般会这么几个处理手段：

·尝试设置更多的特征
·增加多项式特征
·减少λ的值

如果出现高方差，那么有以下几个处理手段：

·获取更多的训练样本
·设置更少的特征
·增大λ的值

三、偏差或方差与神经网络

我们已经看到，高偏差或高方差都会对算法性能造成不良的影响，神经网络如此成功的原因之一就是神经网络与大数据或希望拥有大数据模型的理念相结合，为我们提供了一种解决高偏差和高方差的新方法

在神经网络出现以前，机器学习工程师常常讨论这种偏差-方差权衡，我们必须平衡复杂性，也就是多项式的阶数或者正则化参数λ使得偏差和方差都不太高，如果我们听到机器学习工程师谈论偏差-方差权衡，如果模型太简单，偏差就高，模型太复杂，方差就高，我们必须在它们两个坏结果之间找到一个平衡点，但事实证明神经网络给我们提供了一种方法，可以摆脱偏差和方差之间进行权衡的困境

神经网络在小到中等大小的数据集上进行训练时，是低偏差的机器，意思是如果我们把神经网络做的足够大，几乎总是可以很好地拟合训练集，只要我们的训练集不是很大，这意味着给了我们一个新的方法，可以根据需要降低偏差或方差，而不需要真正权衡两者之间

首先在训练集上训练我们的算法，然后问，它在训练集上表现好吗？所以测量Jtrain看看它是否很高，这里的高是相对于人类水平的表现或者是某个基准的表现，如果表现不佳，那么我们就有个高偏差的问题，解决高偏差问题一种方法是使用更大的神经网络，即更多的隐藏层和每层更多的神经单元，然后我们继续这个循环，知道Jtrain表现良好，然后我们再问，它在交叉验证集上的表现好吗？然后测量Jcv看看它与Jtrain是否相差很大，如果有高方差的问题，那么解决的办法是增加训练模型的数据，并再次回到远点，问是否在训练集上的表现好吗，再重复上述步骤，知道它再交叉训练集上的表现很好，这样就能推广到其他样本身上了

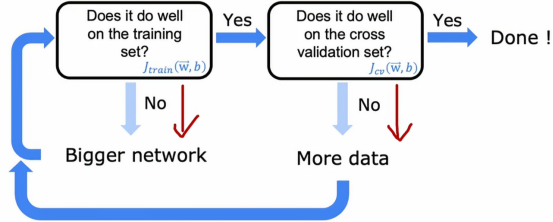
但这样的方法是有局限性的，训练更大的神经网络确实可以减少偏差，但到某个时候，它在计算上会变得非常昂贵，这就是为什么神经网络的兴起真正得到了非常快速的计算机的帮助，尤其是GPU和图形处理单元，硬件通常用于加速计算机图形，但事实证明，它们对于加速神经网络也非常有用，但即使有硬件加持，但到了一定程度上，神经网络太大、训练时间太长，最终还是变得不可行，并非无限成长，当然另外一个限制是更多的数据，有时候我们只能获得一定量的数据，超过某个点之后很难再获得更多的数据。

但我们不要被大神经网络吓傻了，不敢尝试更大的神经网络，害怕导致高方差问题，事实证明，一个经过良好正则化选择的大型神经网络通常会表现的和小网络一样优秀，甚至比小网络更加优秀，我们固有思维就是当我们从小网络进化到大网络的时候，我们会认为过拟合的风险会增加，但我们主要对这个大型神经网络进行适当的正则化，那么这个较大的神经网络会表现的和小型的一样优秀甚至更好，换句话说，使用正则化在大型神经网络里没有任何坏处，唯一要注意的是，当我们训练一个较大的神经网络，它确实会变得更难计算，所以主要的影响它会减慢我们的训练过程和推理过程

1、正则化代码

下面是运用了正则化的代码

# Unregularized MNIST model
layer_1 = Dense(units=25, activation="relu")
layer_2 = Dense(units=15, activation="relu")
layer_3 = Dense(units=1, activation="sigmoid")
model = Sequential([layer_1, layer_2, layer_3])# Regularized MNIST model
layer_1 = Dense(units=25, activation="relu", kernel_regularizer=L2(0.01))
layer_2 = Dense(units=15, activation="relu", kernel_regularizer=L2(0.01))
layer_3 = Dense(units=1, activation="sigmoid", kernel_regularizer=L2(0.01))
model = Sequential([layer_1, layer_2, layer_3])

上面是没有应用正则化，下面是运用了正则化，我们发现，只要在每层的定义中，加一个kernel_regularizer = L2()即可，括号内的值就是λ的值

总结

今天的学习让我掌握了通过学习曲线来诊断模型问题的方法。当训练误差和验证误差都很高时，说明模型存在高偏差，这时候增加数据量帮助不大，需要增加特征或使用更复杂的模型。当训练误差很低但验证误差很高时，说明存在高方差，增加训练数据通常能有效改善性能。在神经网络中，我们可以通过构建更大的网络来降低偏差，同时配合正则化技术来防止过拟合。最后在代码实践中，我学会了如何在TensorFlow中使用L2正则化，只需要在每层添加kernel_regularizer=L2(0.01)参数即可。这些知识让我对模型调优有了更系统的认识，知道了在不同情况下应该采取什么样的优化策略。