《考研408数据结构》第七章(6.1~6.3图的概念、存储方式、深/广度遍历)复习笔记
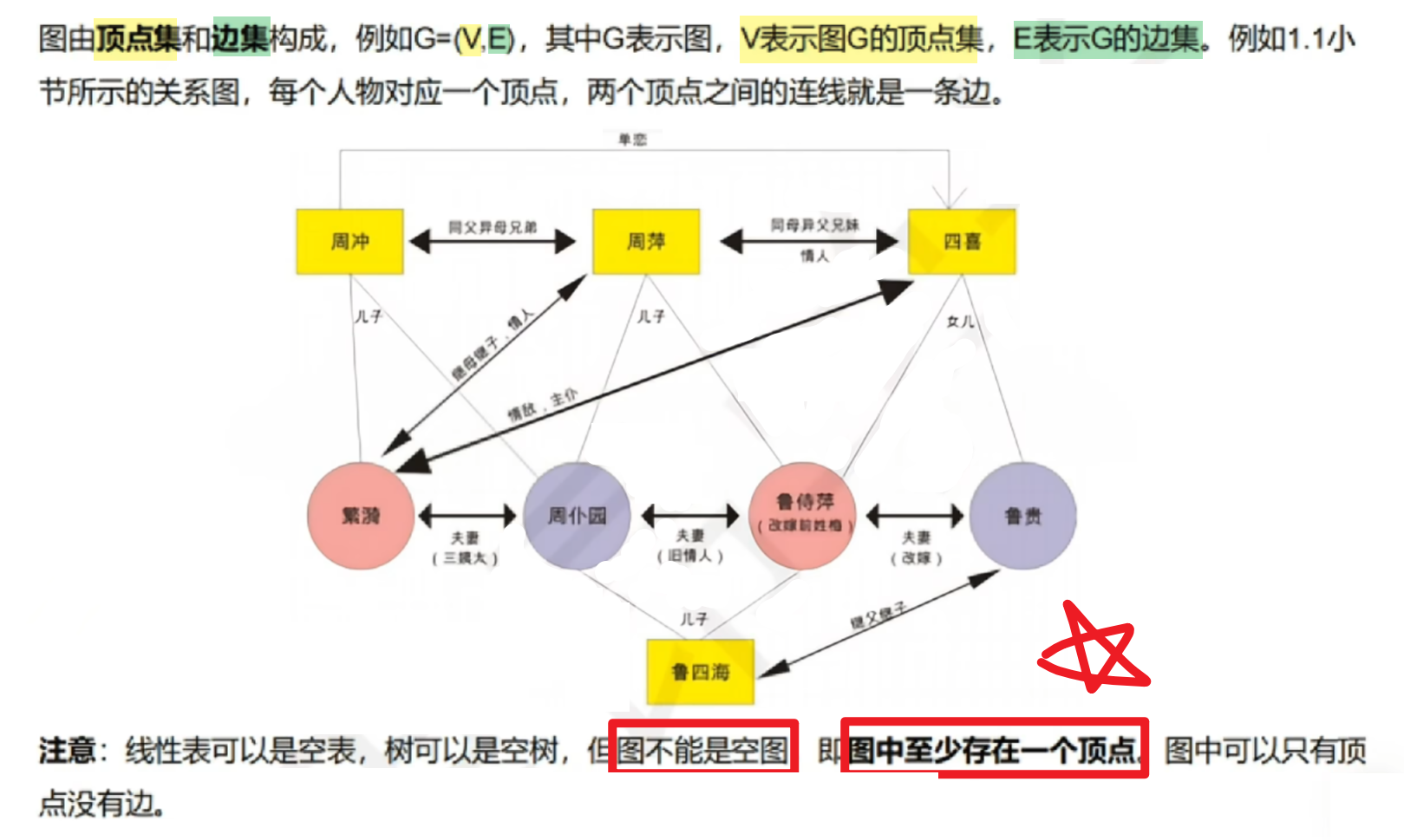
一、图的定义
【基本概念】
1、【无向图】、【有向图】、【简单图 和 多重图】
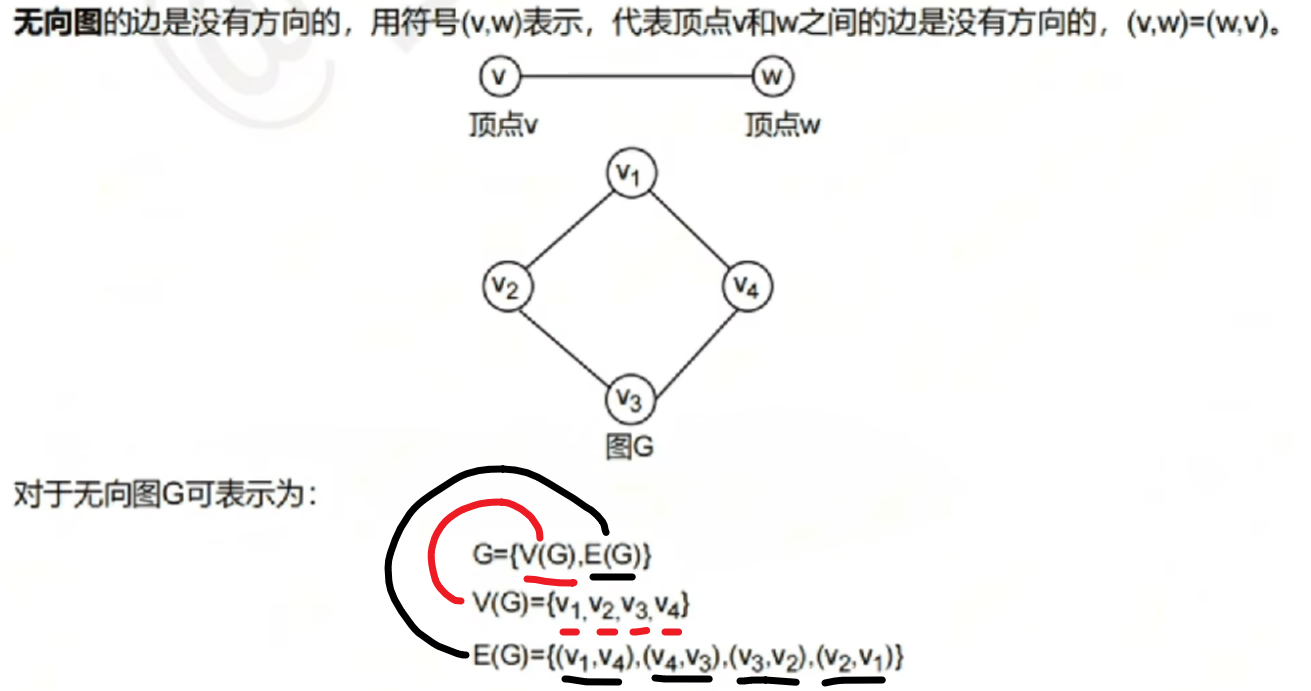
【无向图】
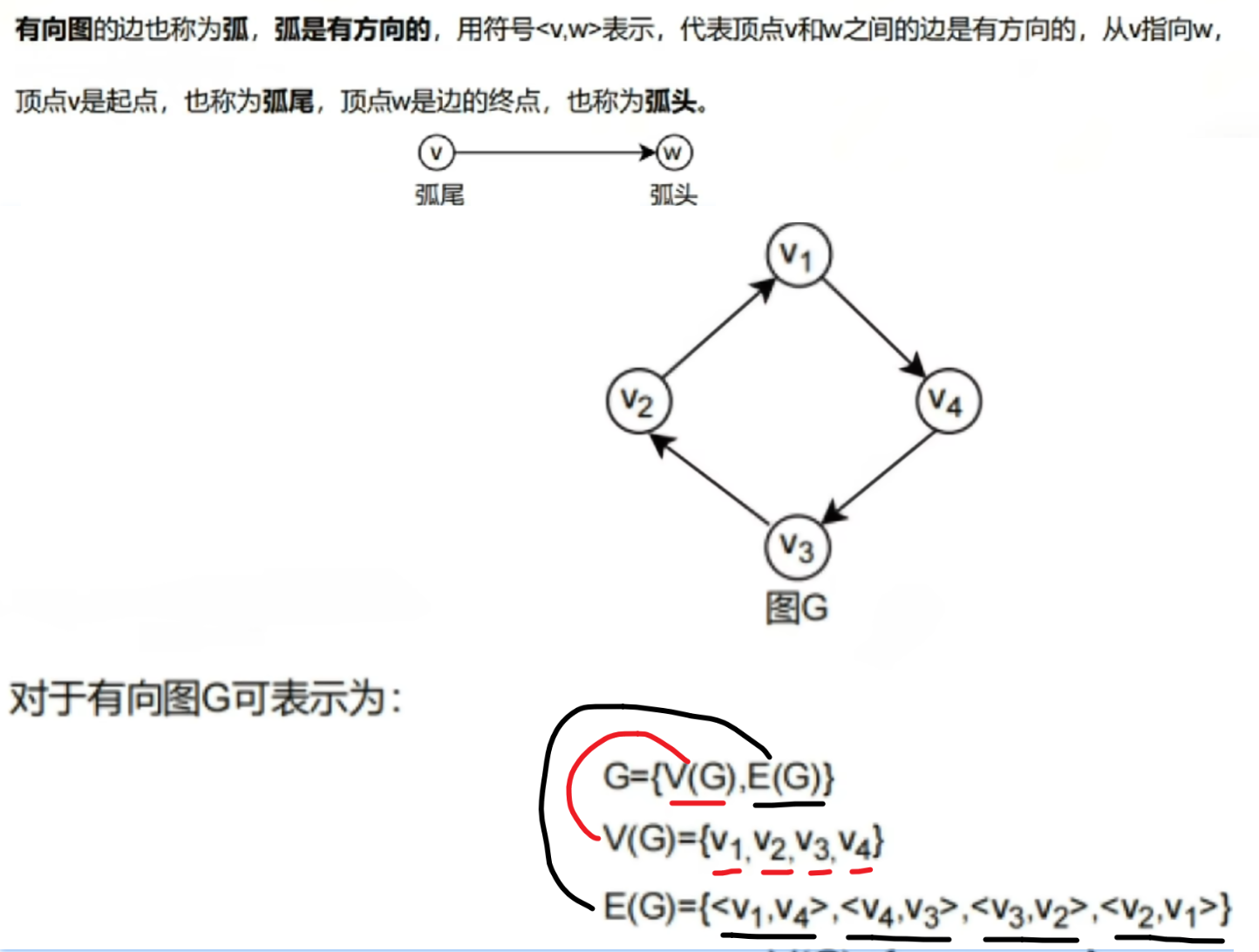
【有向图】
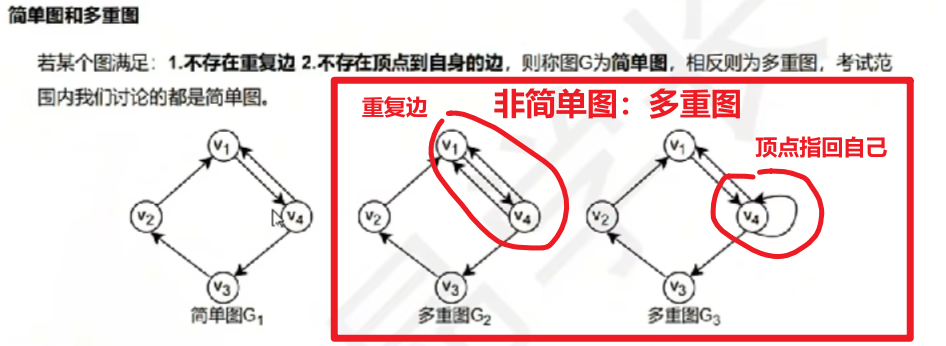
【简单图 和 多重图】
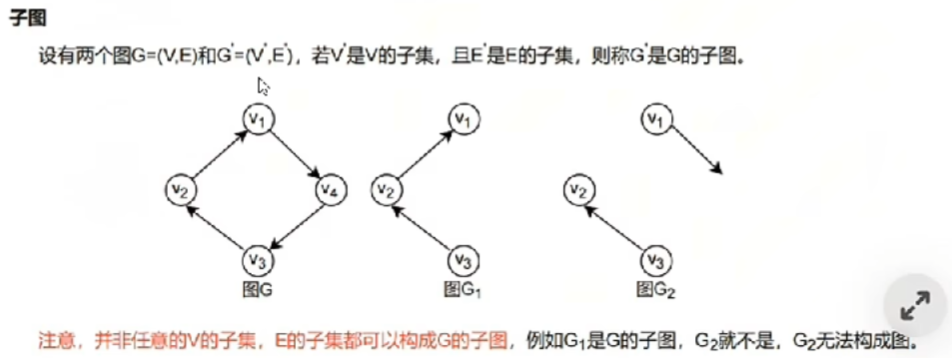
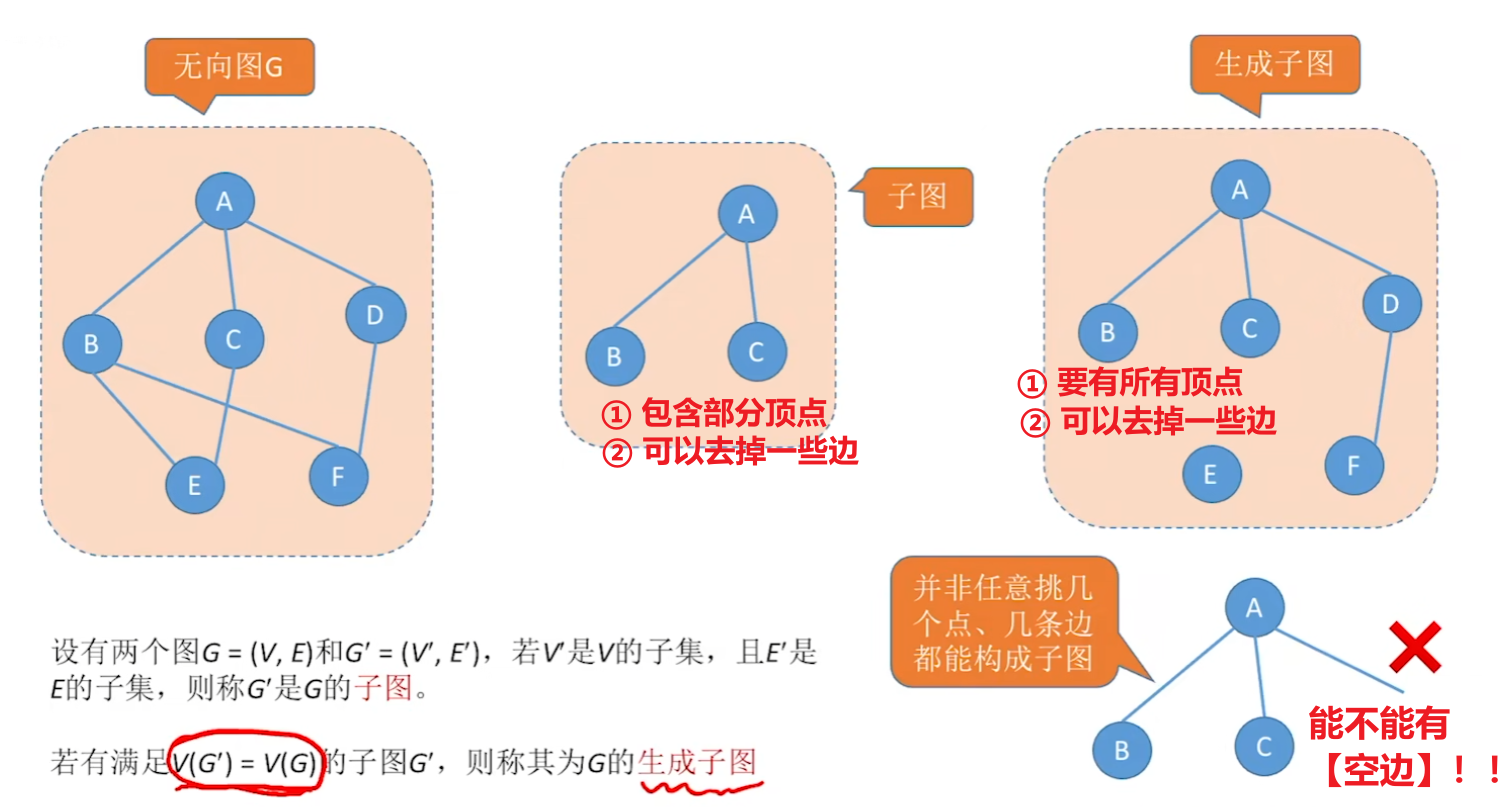
2、【子图】、【生成子图】
只要记住:
- 【子图】含部分顶点、【生成子图】含全部顶点
- 然后它两可以没有一些边,但绝对不能有【空边(没有顶点可以指向)】
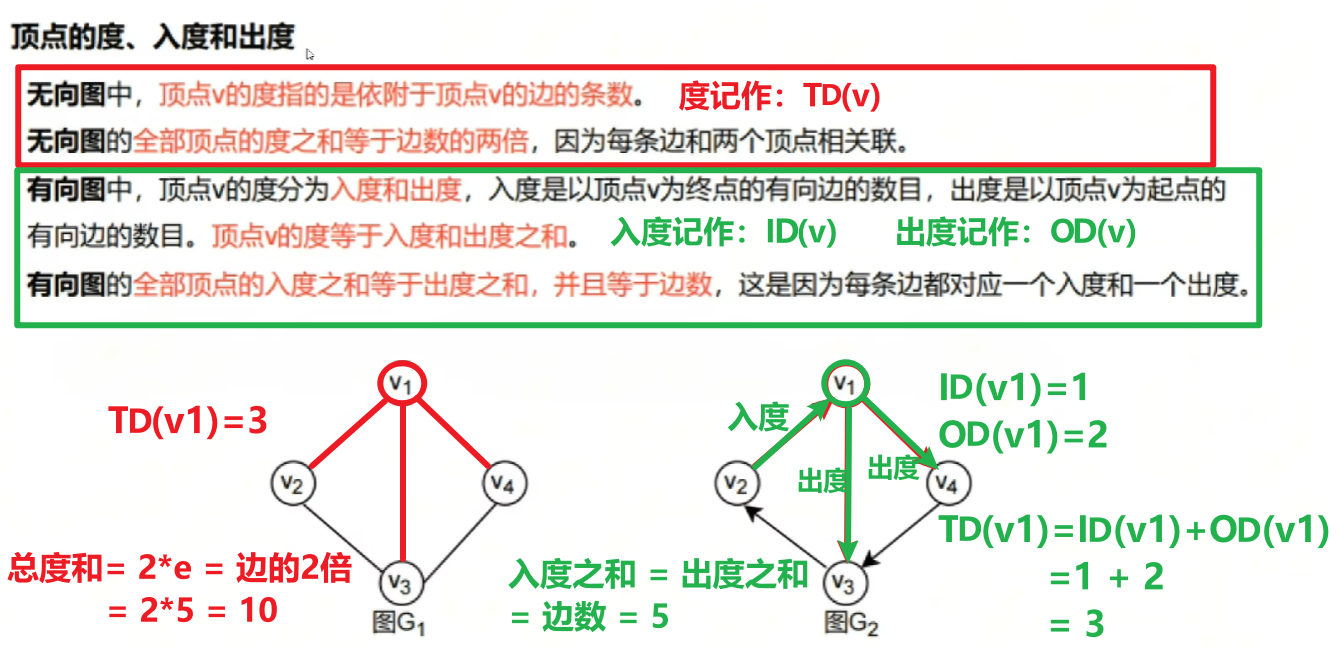
3、【顶点的度】、【路径】
【顶点的度】
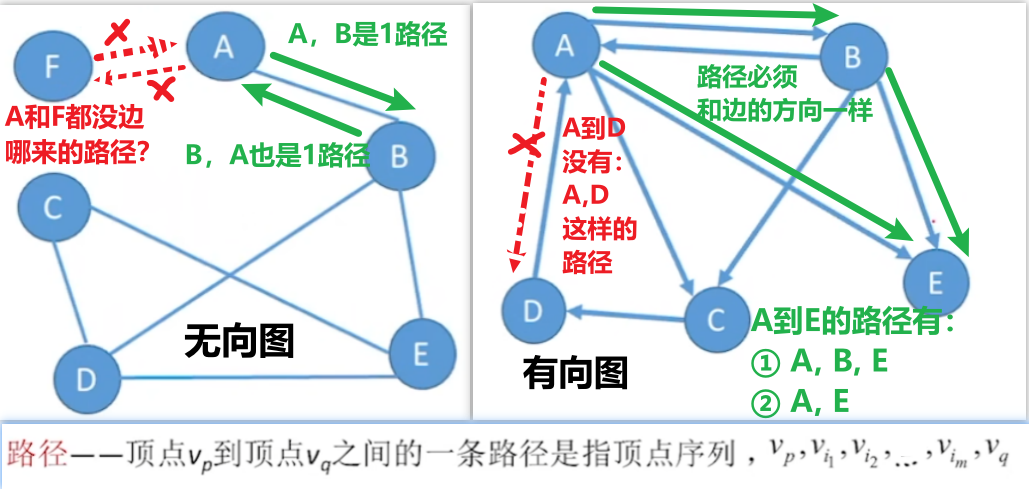
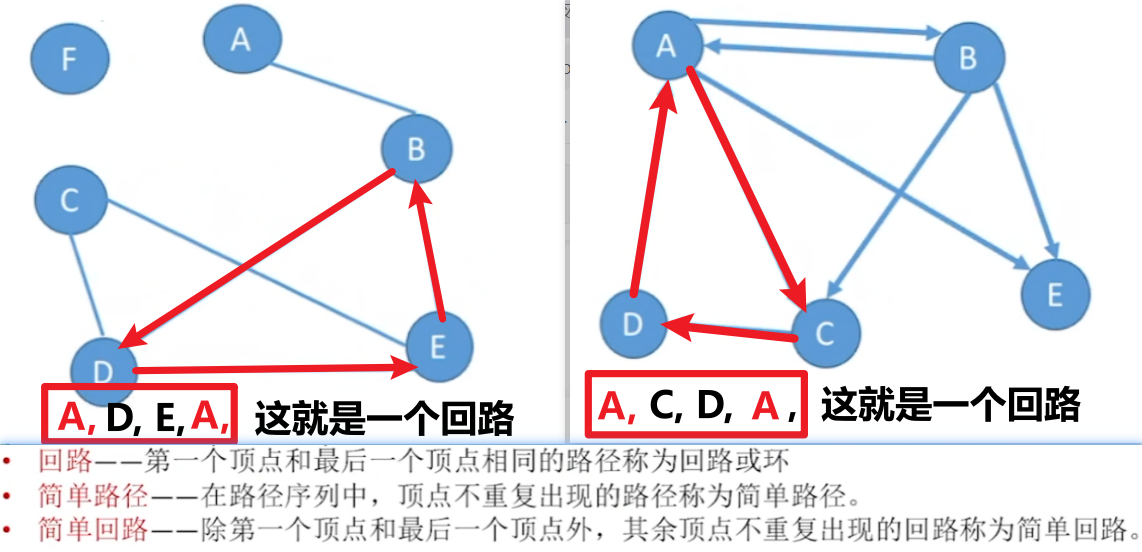
【路径】、【回路】、【路径长度】
- 一点到另一点的【路径】起码得有边!!!(想象实际生活:你A岛 到 B岛都没修路,哪来的路径?)
- 无向图,A点到B点只要有边,A,B、B,A都算路径;
- 而有向图,路径只能和边的方向一样,<A,B>的路径只有A,B
- 【回路】就是这条路径【开头=结尾】,也就是【起点绕了一圈回到自己】
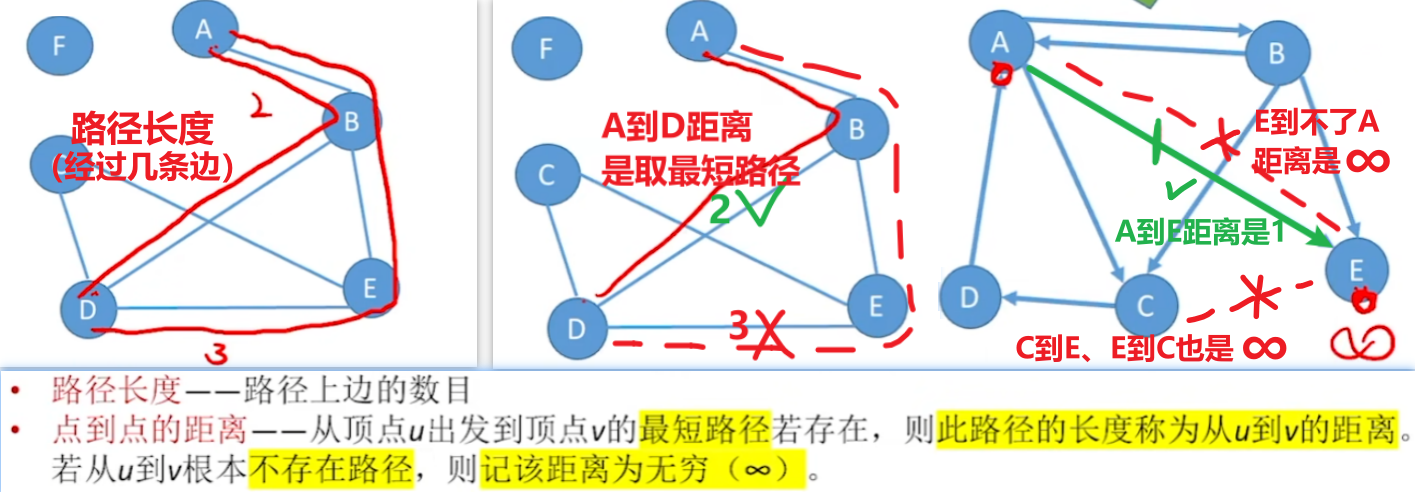
- 【路径长度】和【点到点距离】
- 【路径长度】顾名思义,起点到终点所经过几条边
- 【距离】就是取两点【最短路径】,【没有路径】就取【无穷 ∞】
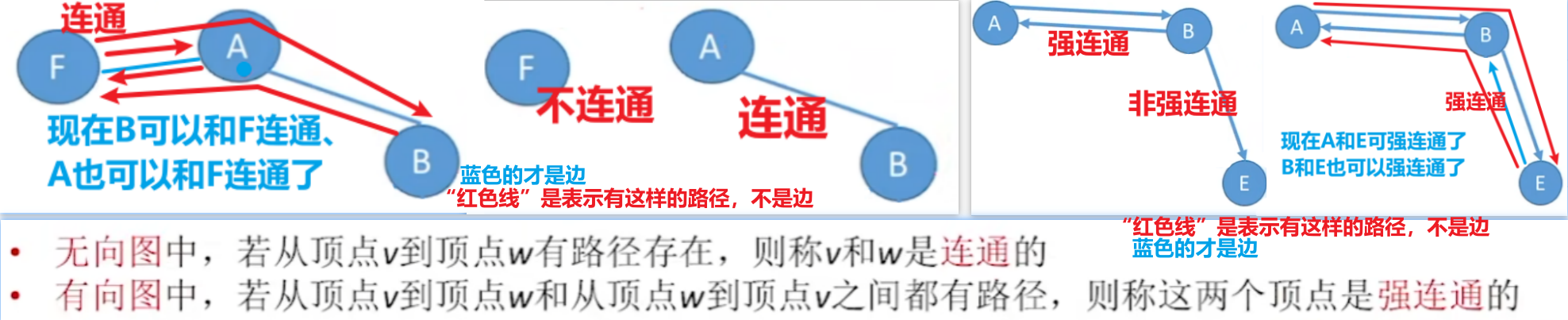
【连通、连通图、连通分量】
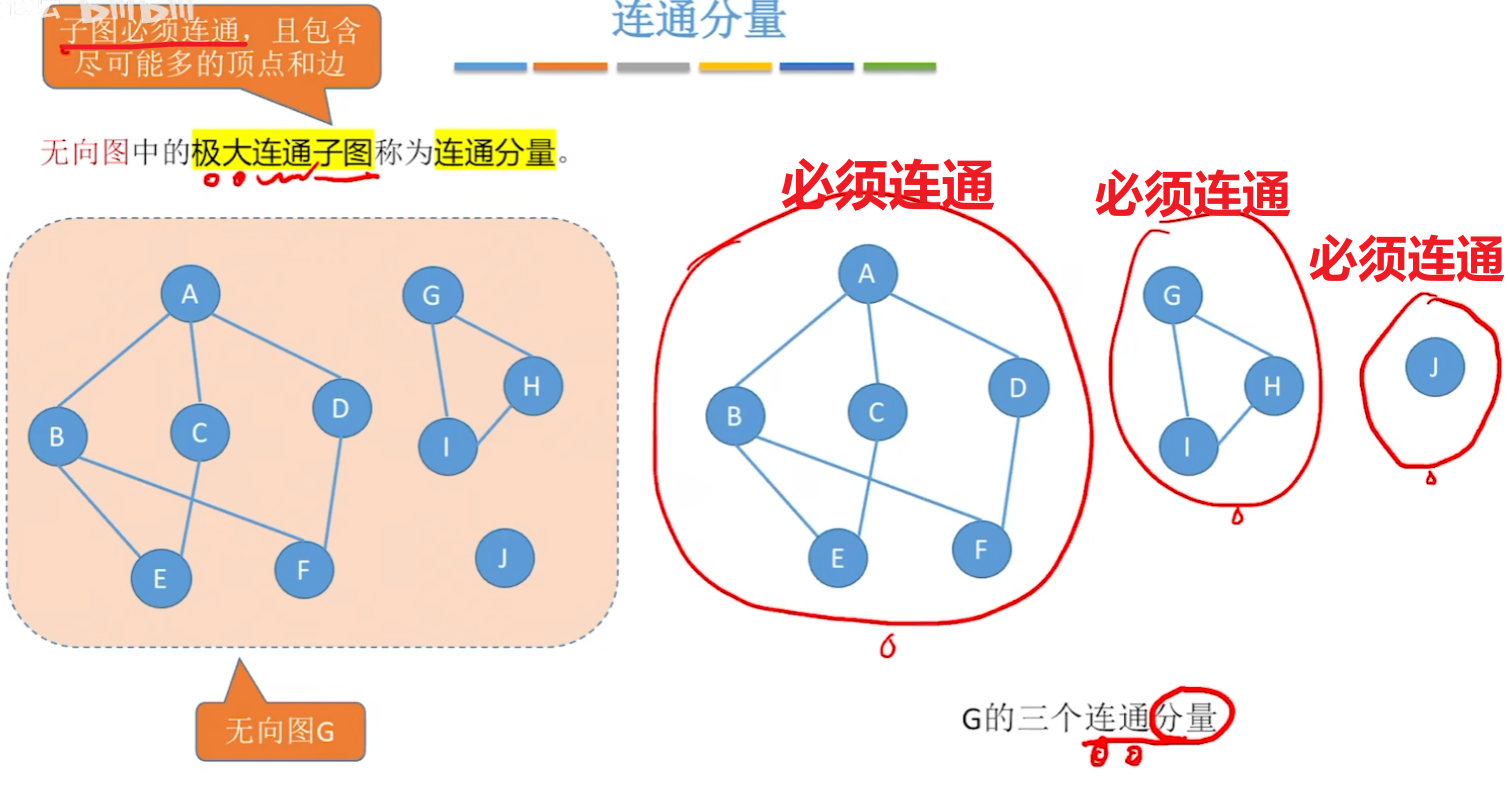
- 【连通、连通图、连通分量】概念全部对应【无向图】
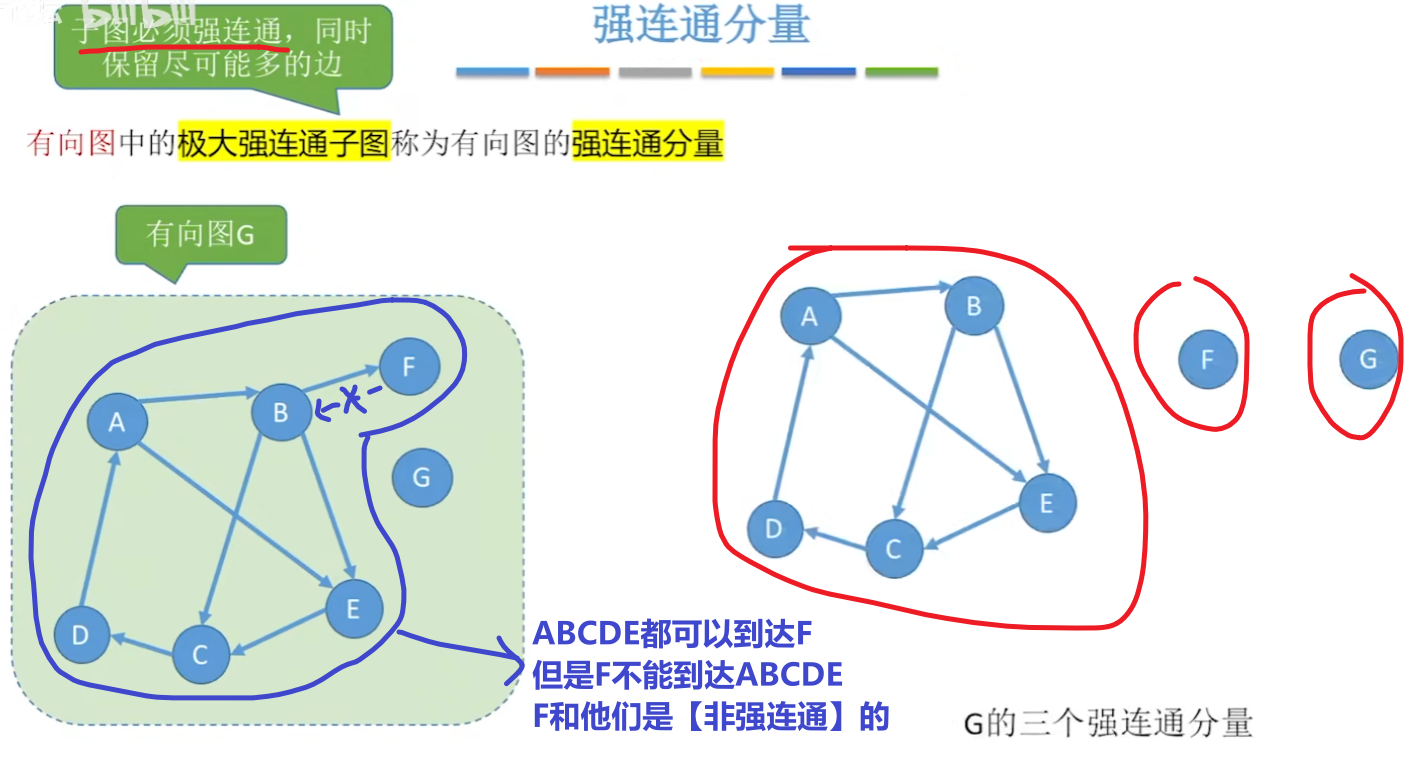
- 【强连通、强连通图、强连通分量】概念全部对应【有向图】
;
- 1、具体【连通】和【强连通】概念
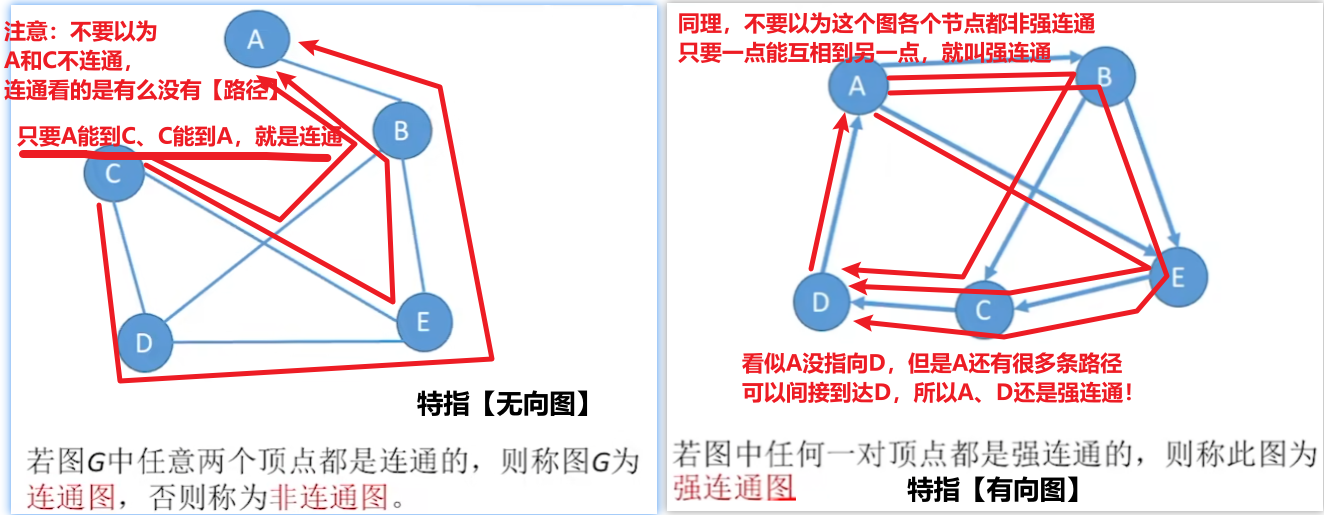
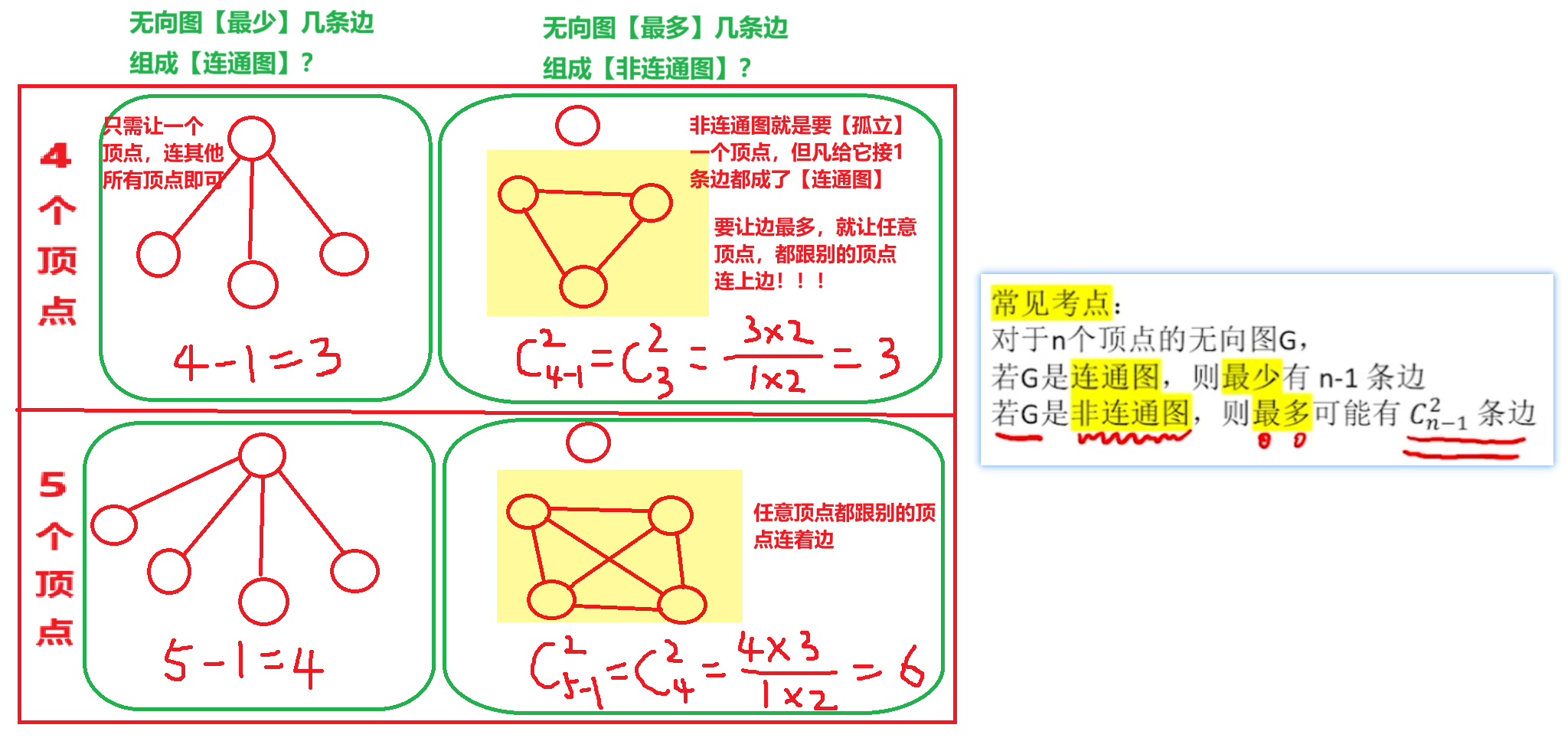
- 2、【连通图】和【强连通图】概念
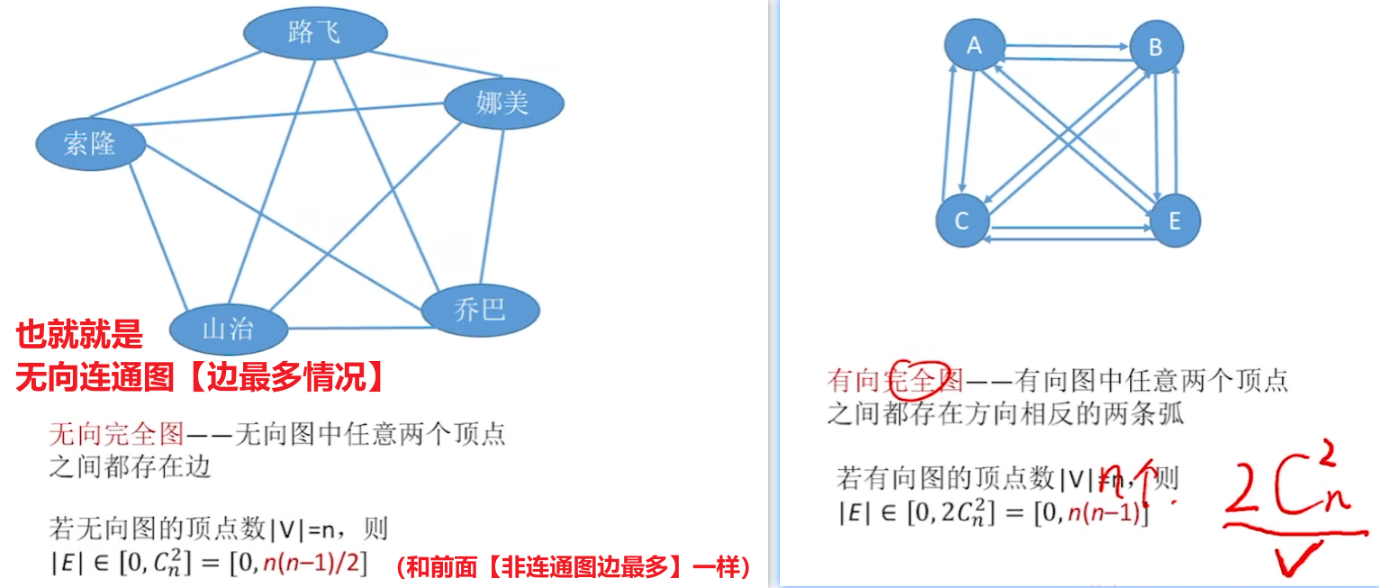
- 注意【连通图最少边】、【非连通图最多边】计算
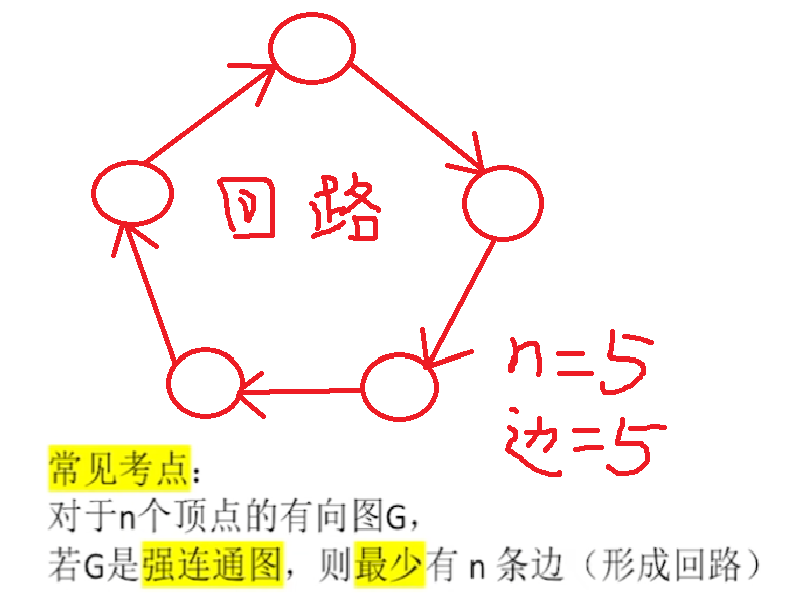
- 【强连通图最少边】计算
- 3、【连通分量】和【强连通分量】
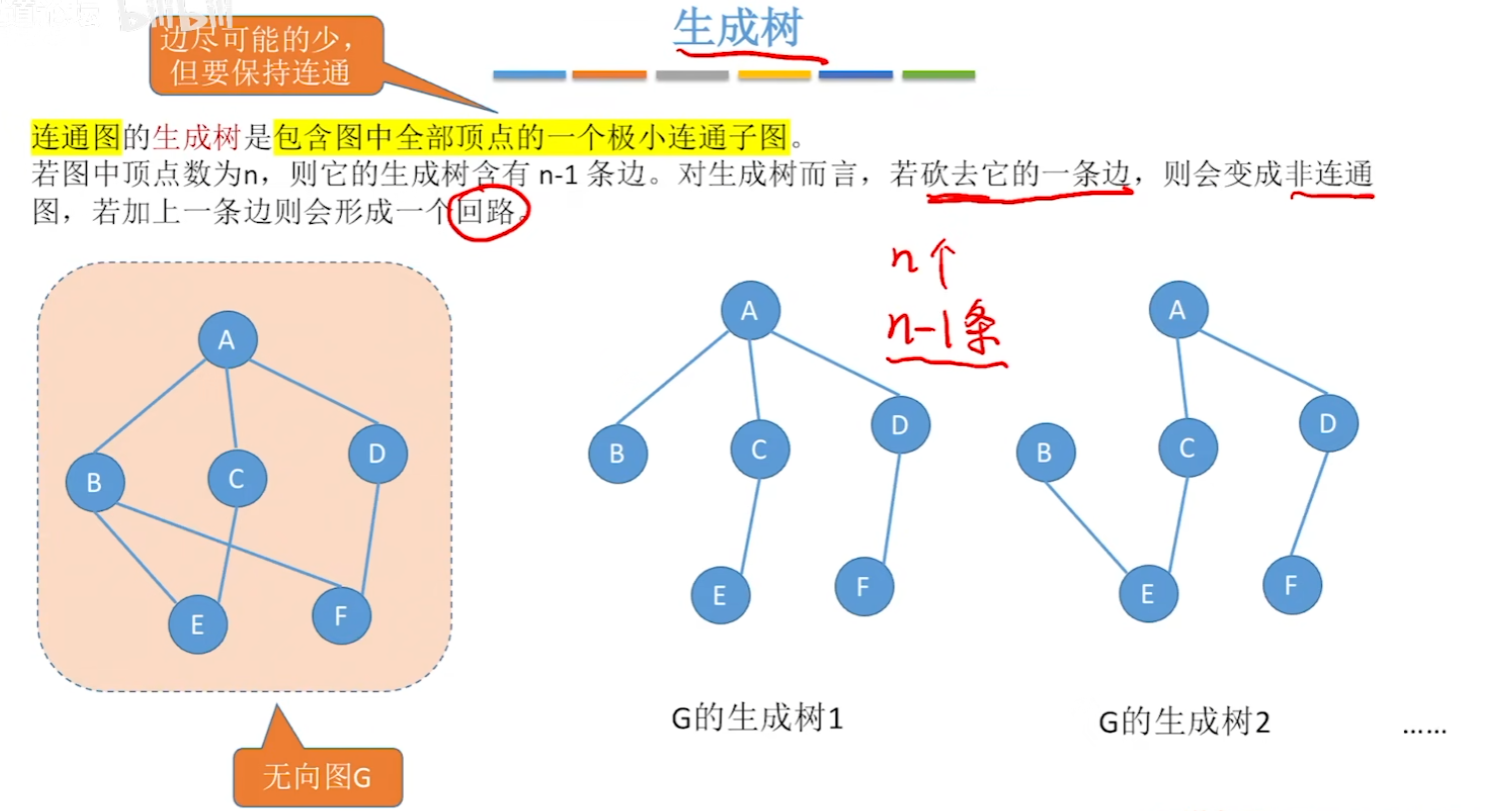
【生成树】、【生成森林】
- 【生成树】就是【极小连通图】
- 其实【生成树 的 边数】就和前面学得【连通图的最少边情况】一样
- 这样的实际意义就可以理解为:一个城乡修建道路图,有这么多种修路方案,每个修路方案都保证只用修最少的路就能让各个地点连通,在这基础上加上权值的话,就可以选出最优方案了
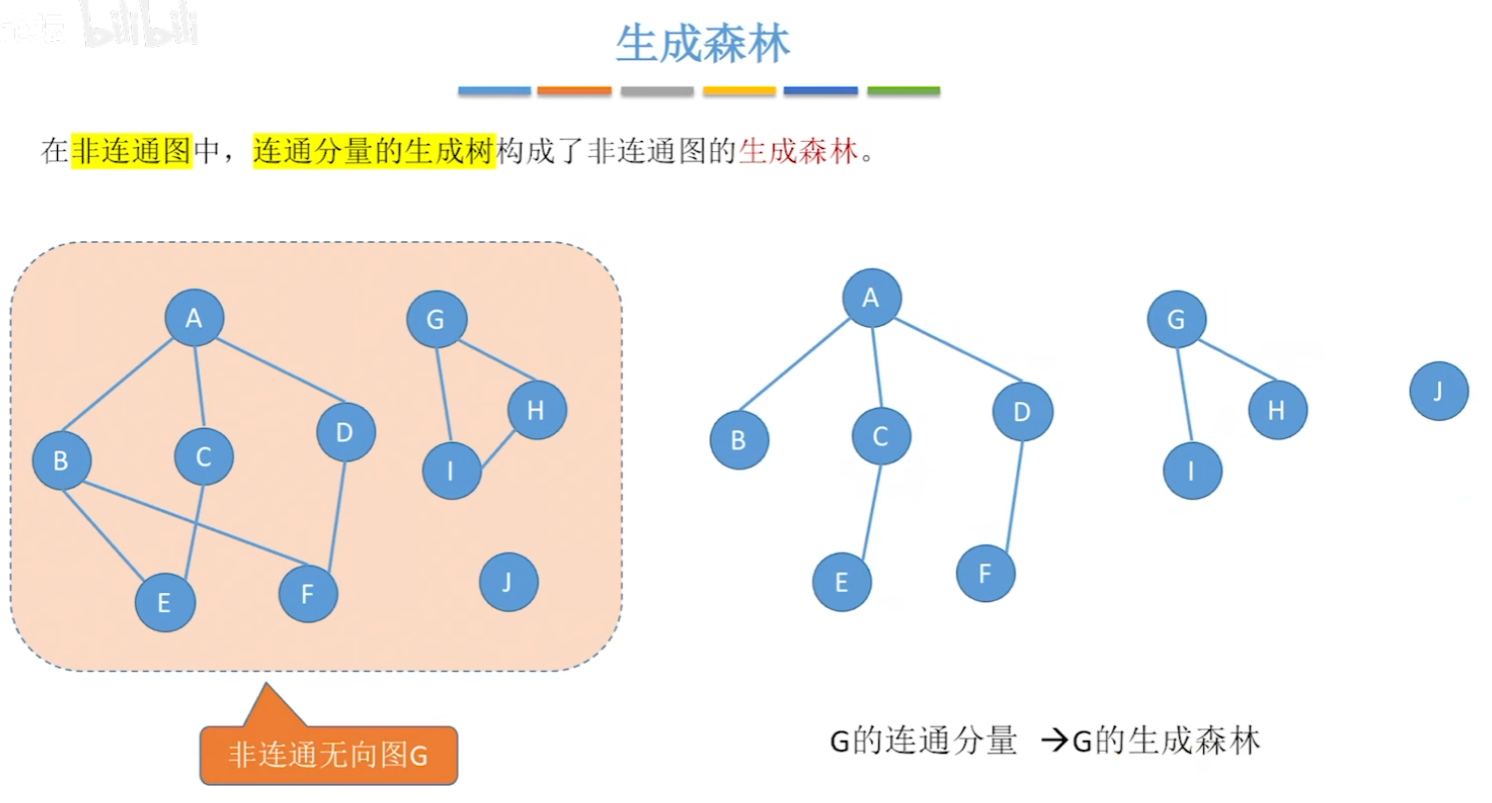
- 【生成森林】就是【各个连通分量——>变成生成树】
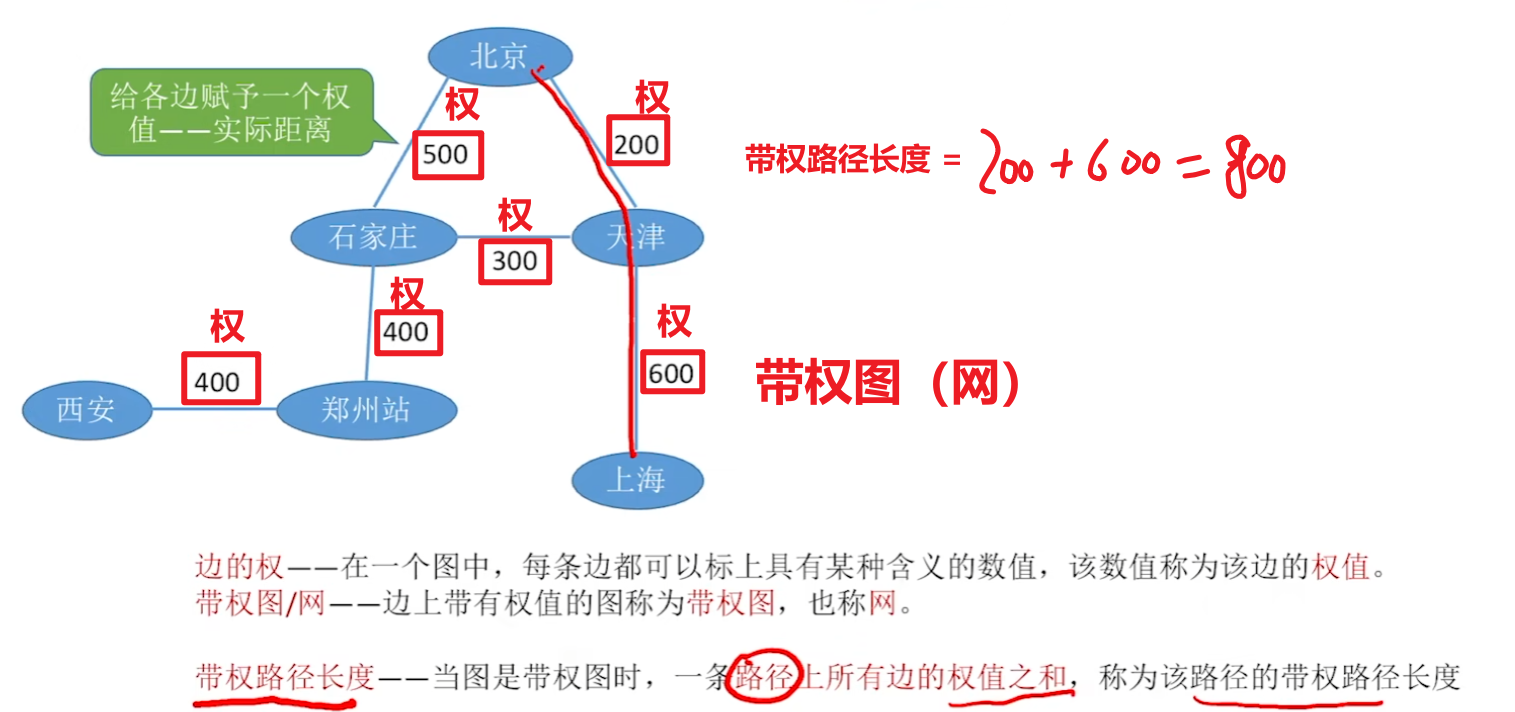
【边的权、网、带权路径长度】
【几种特殊形态的图】
- 【完全图】
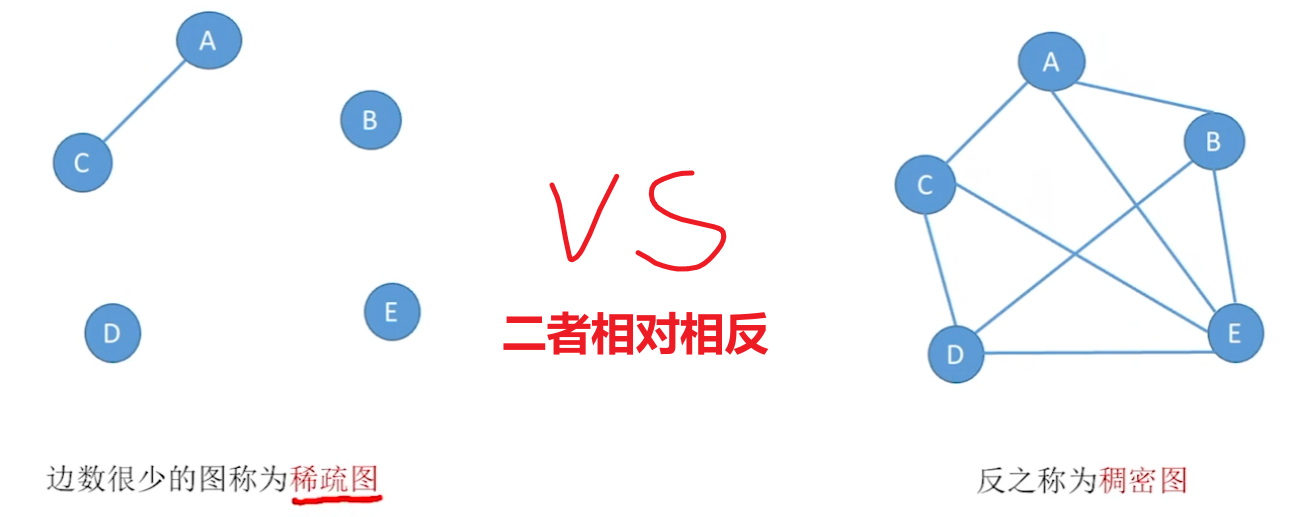
- 【稀疏图 和 稠密图】
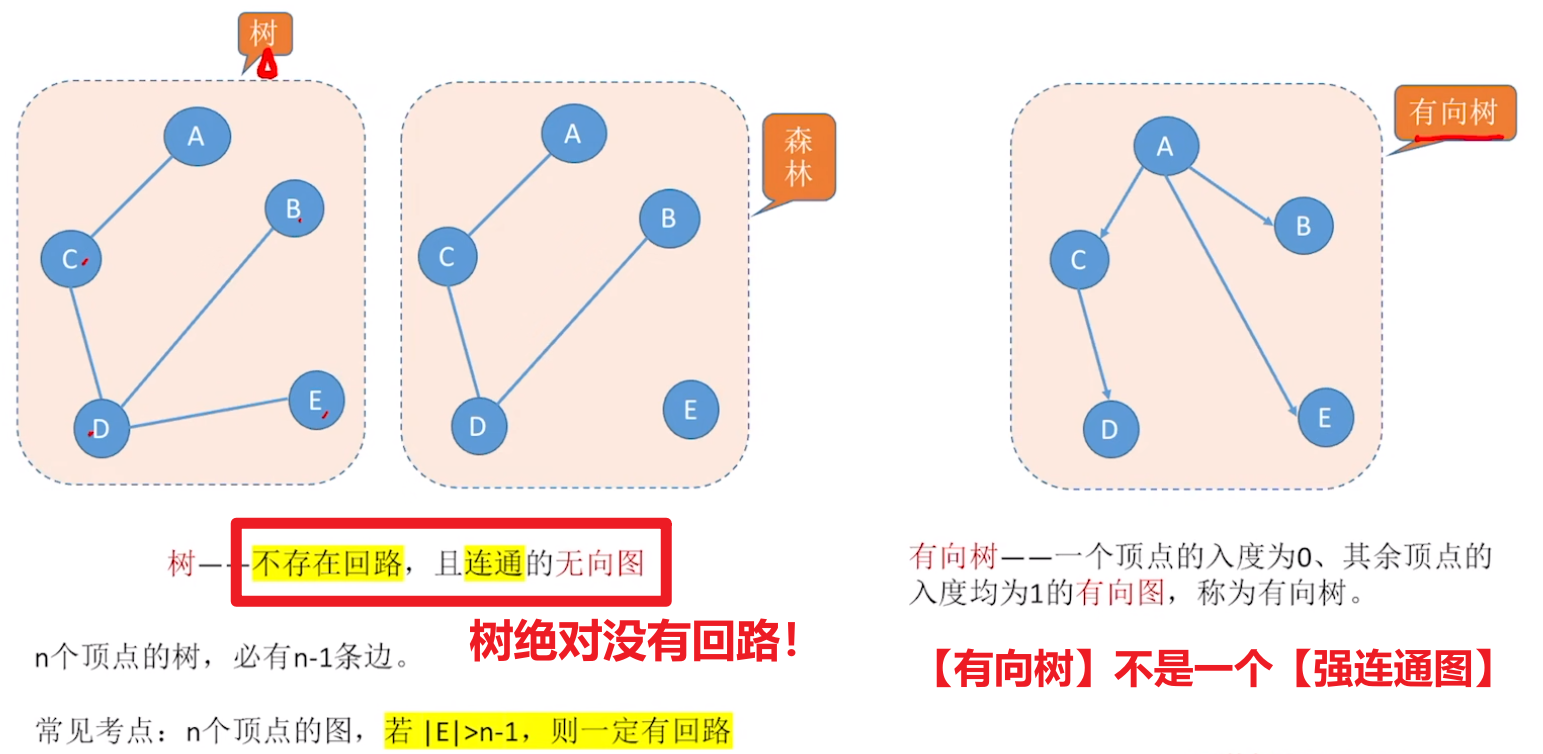
- 【树 和 有向树】
二、图的存储方式种类
1、邻接矩阵法(最常考)
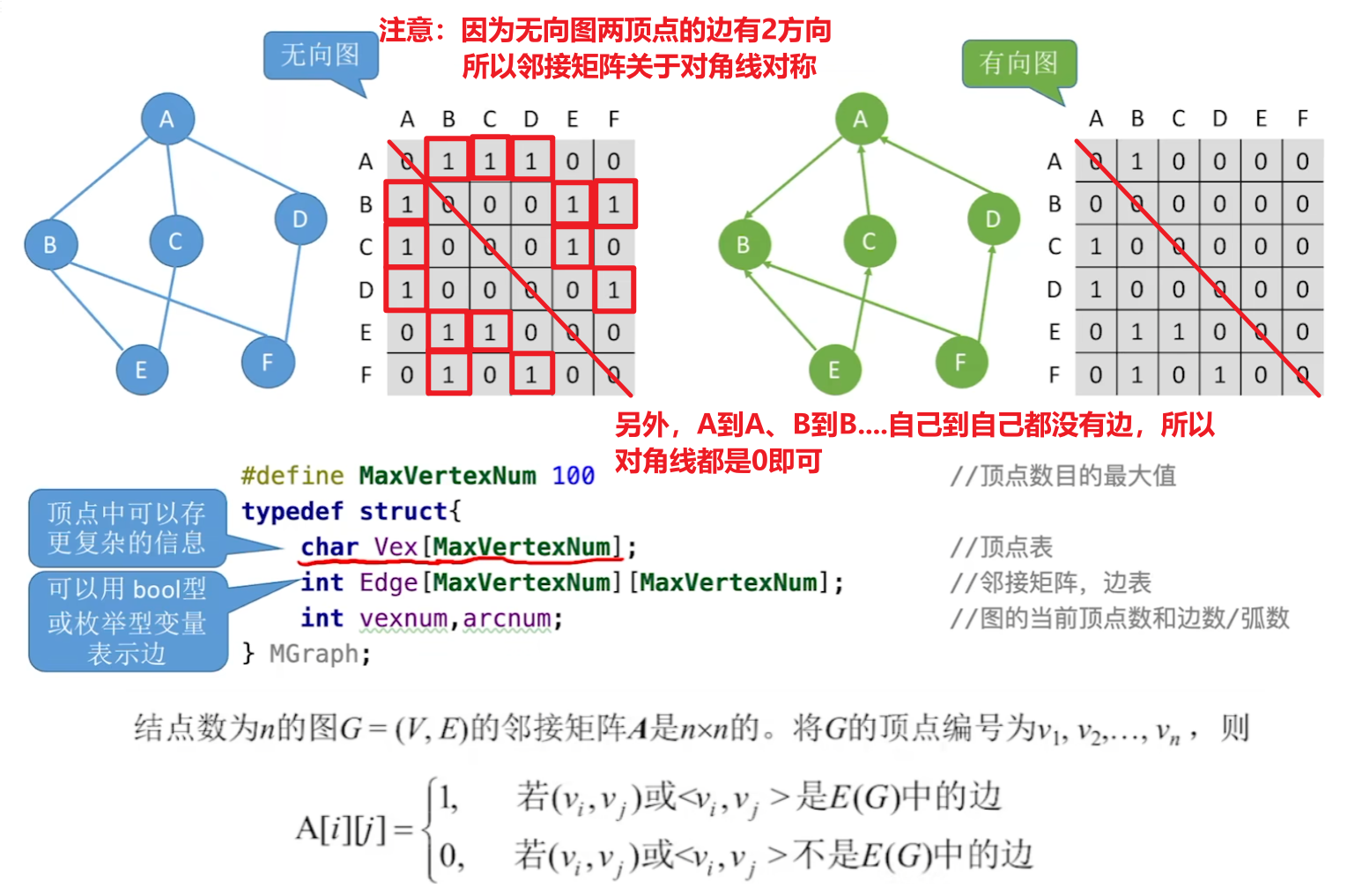
- 1、先了解【无向图】和【有向图】怎么用【邻接矩阵】表示(写法)
- 注意代码可以看一眼就行,以后要练大题的话再专门学一下就行
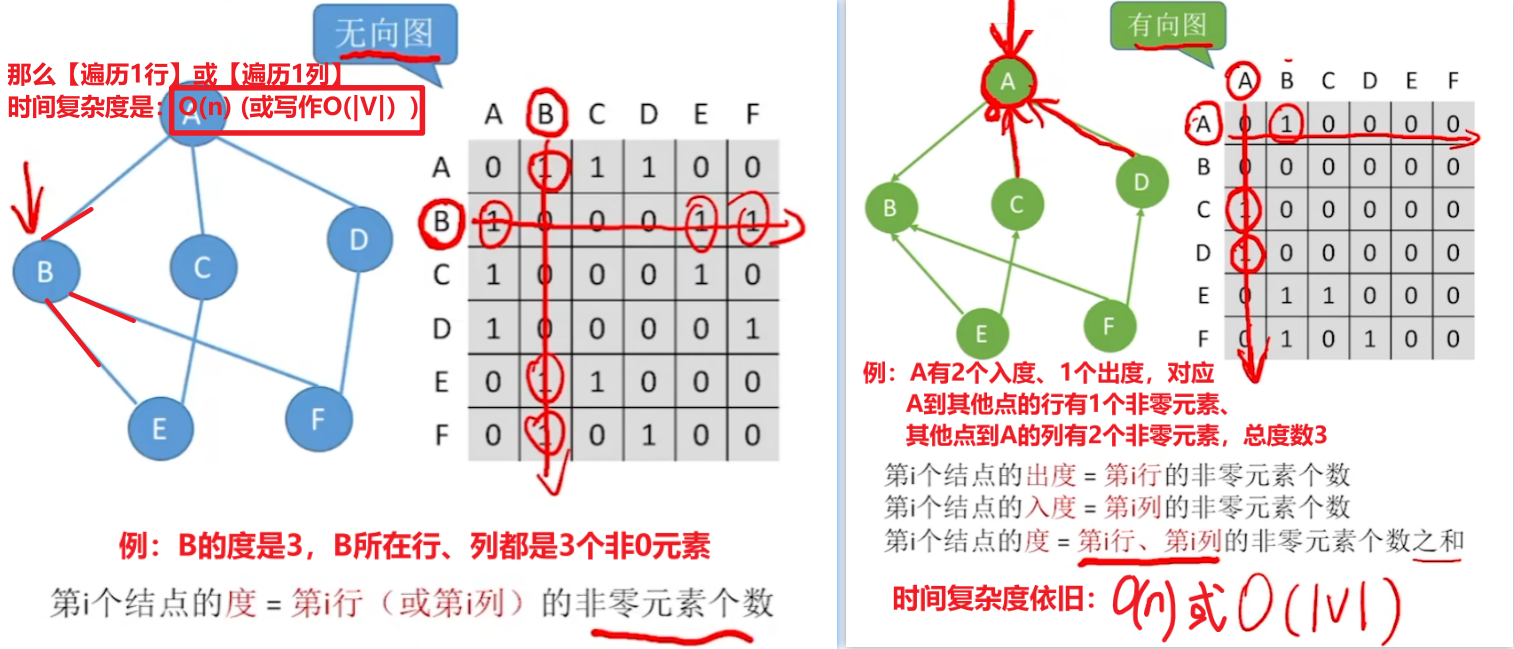
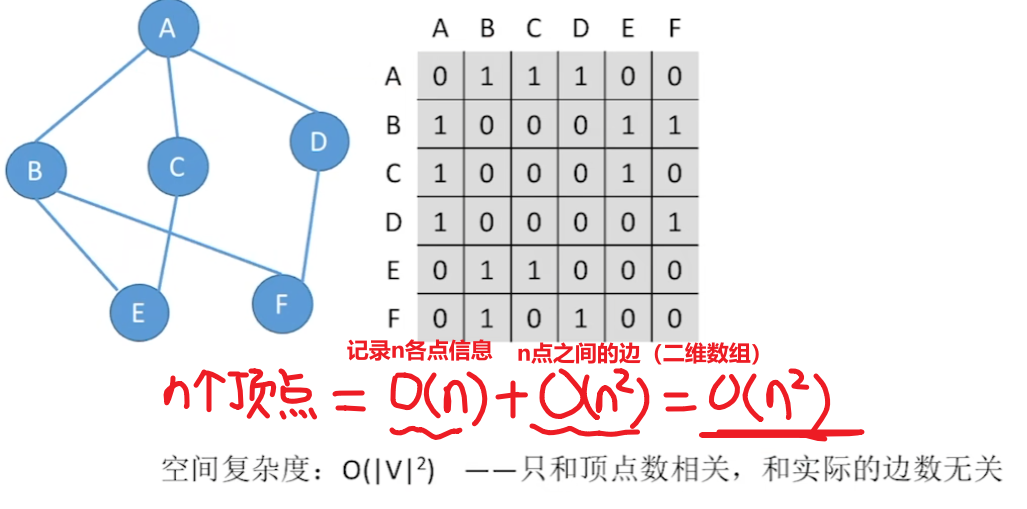
- 2、邻接矩阵【查一个顶点的度】
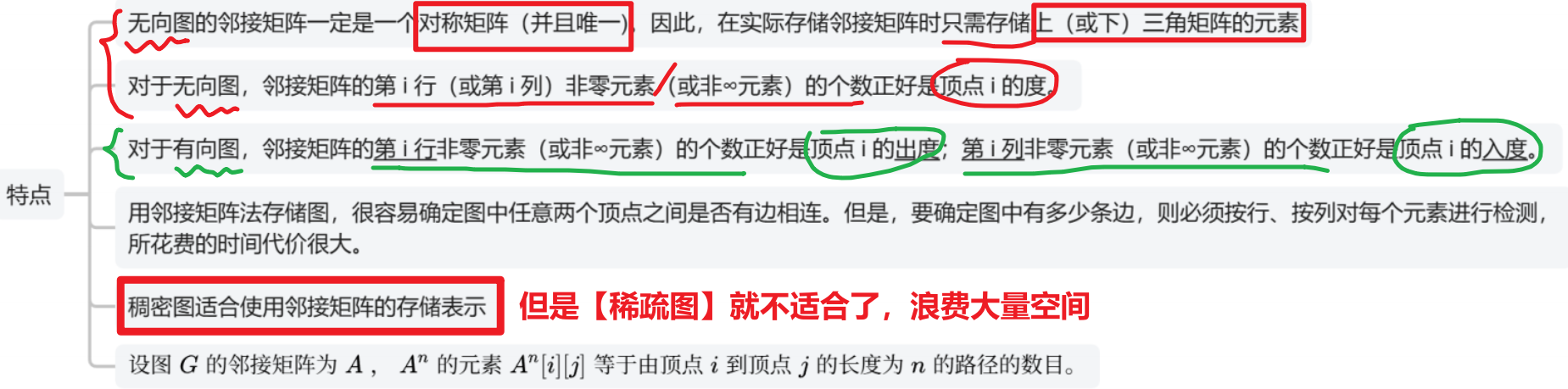
- 【无向图】:该顶点的1行或1列的非零元素个数;
- 【有向图】:【入度】是1列的非零元素;【出度】是1行的非零元素
- 【时间复杂度】:O(n) 或 O(|V|)
- 3、邻接矩阵的【空间复杂度】:O(n^2)
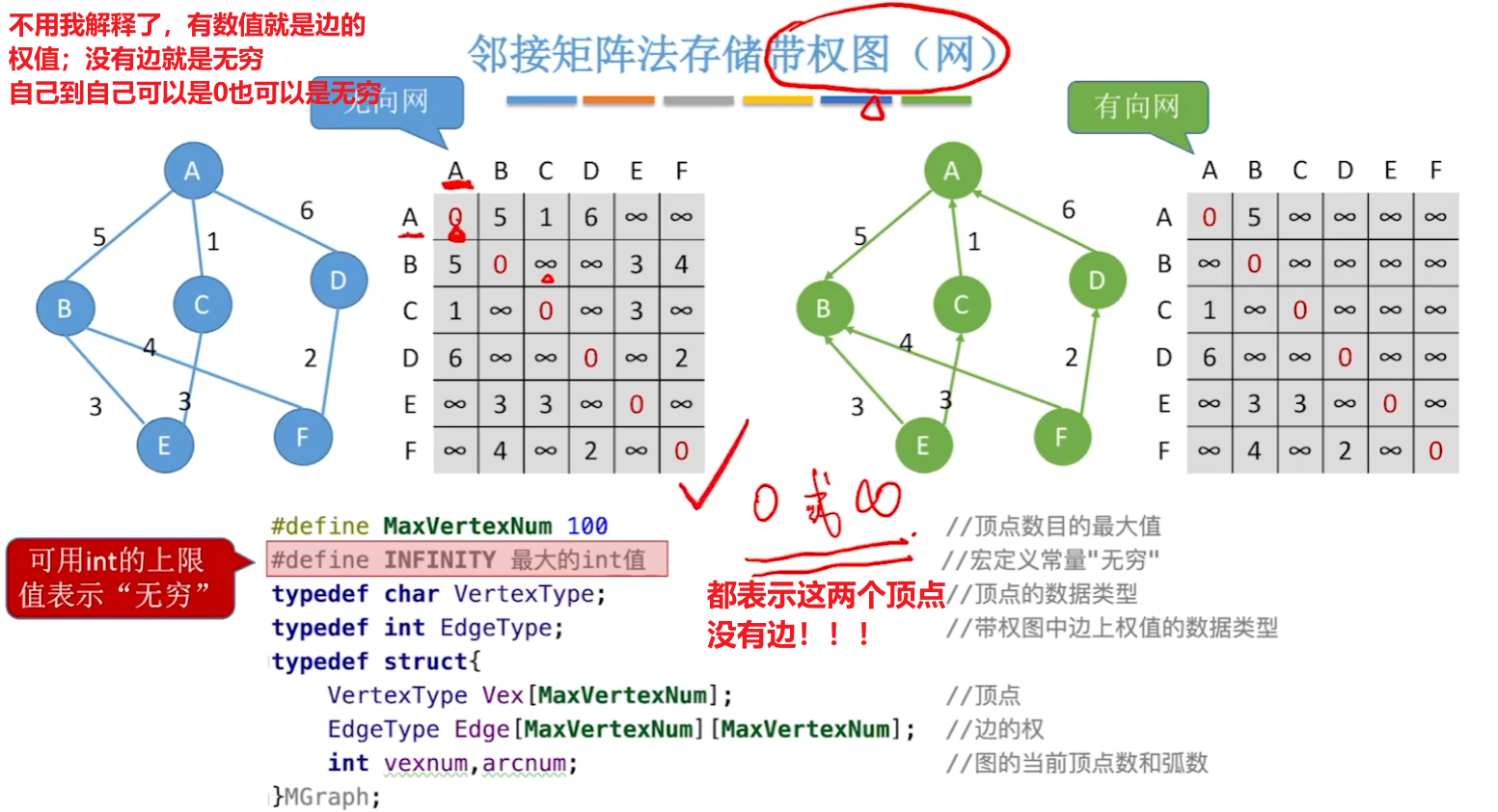
- 4、【带权图(网)】的邻接矩阵表示:就是标上了确切数值,而不只是0、1
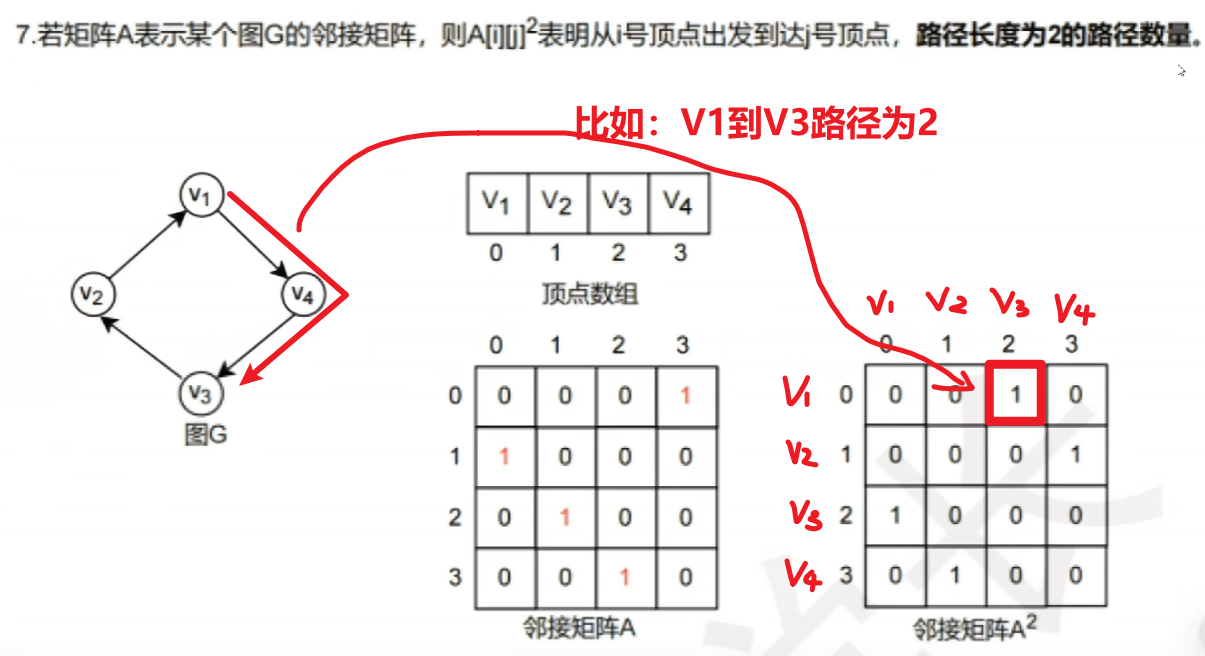
- 5、(不常考)还有一种邻接矩阵是【A[i][j]^n】
- 【n】就是表示这个邻接矩阵里,记录的【值1】表示【这两点的路径是n】
- 记录的【值0】表示【这两点的路径不是n】或【这两点没有边】
【记忆特点】
- 邻接矩阵使用的是【顺序存储】(一维数组、二维数组)
- 【空间复杂度高:O(n^2)】
- 而且【空间跟 “边” 没有关系!!!】
- (注意区分:时间复杂度是O(n))
- 不适合存储【稀疏图】、适合【稠密图】
- 大量顶点之间没有边,却还要用【0 或 无穷】来存储,占用空间
- 而且【增加 / 删除节点】麻烦!!!需要修改整个矩阵结构
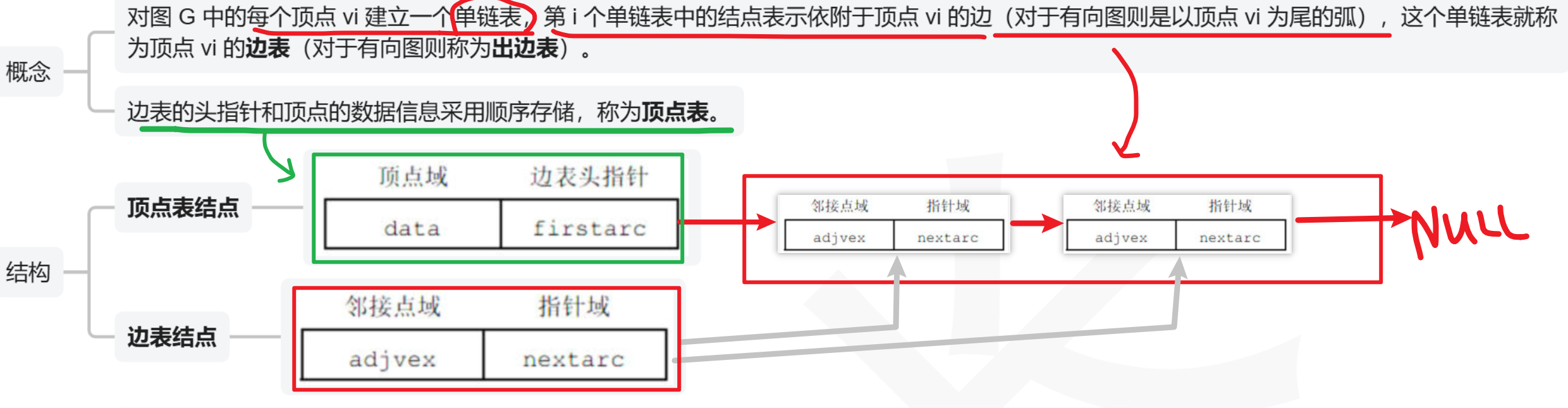
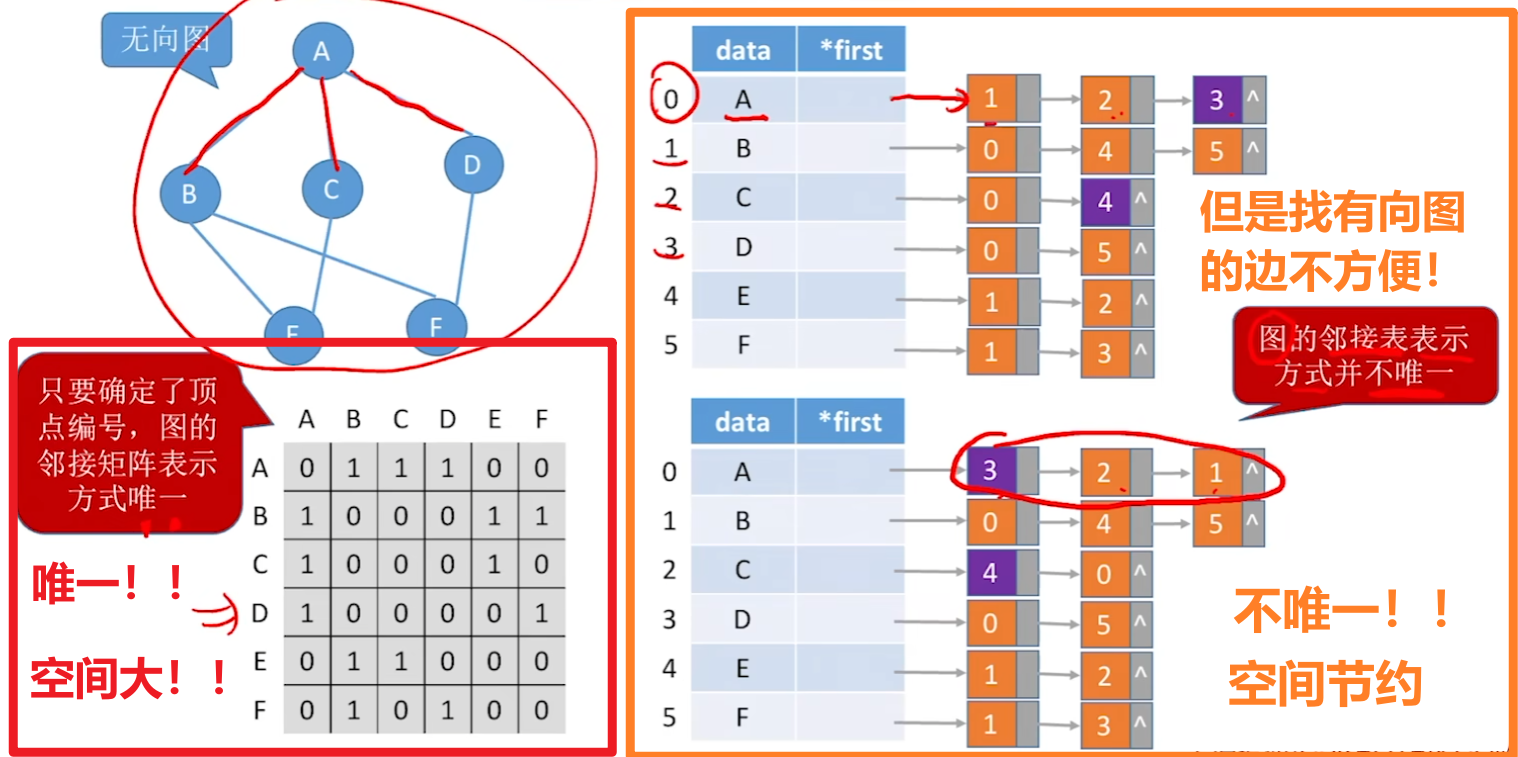
2、邻接表法(次常考)
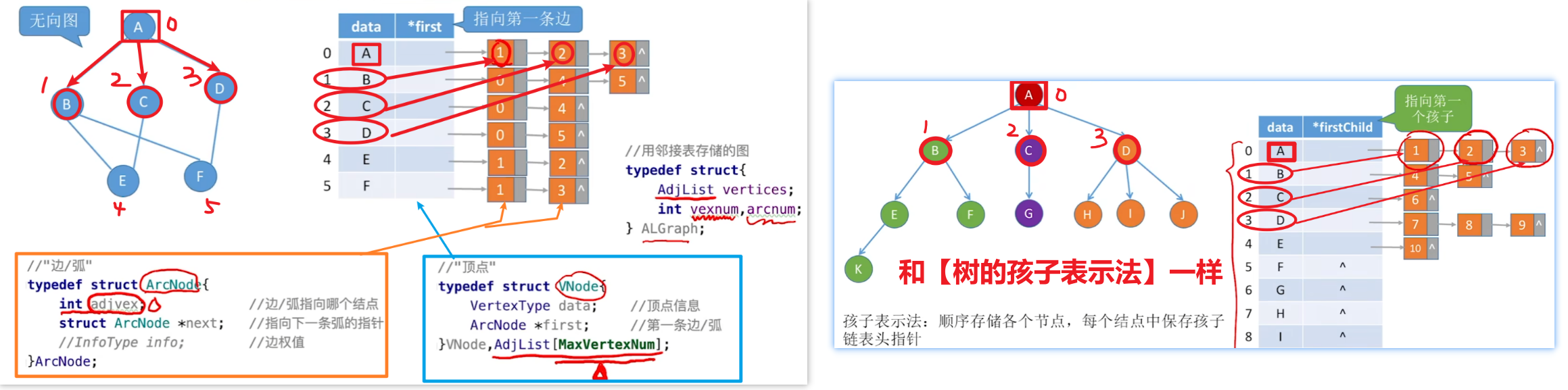
- 1、先了解【无向图】和【有向图】怎么用【邻接表】表示(写法)
- 注意代码可以看一眼就行,以后要练大题的话再专门学一下就行
- 另外这个图可以结合《计网第4章:路由算法》的迪杰斯特拉算法,一样的表示
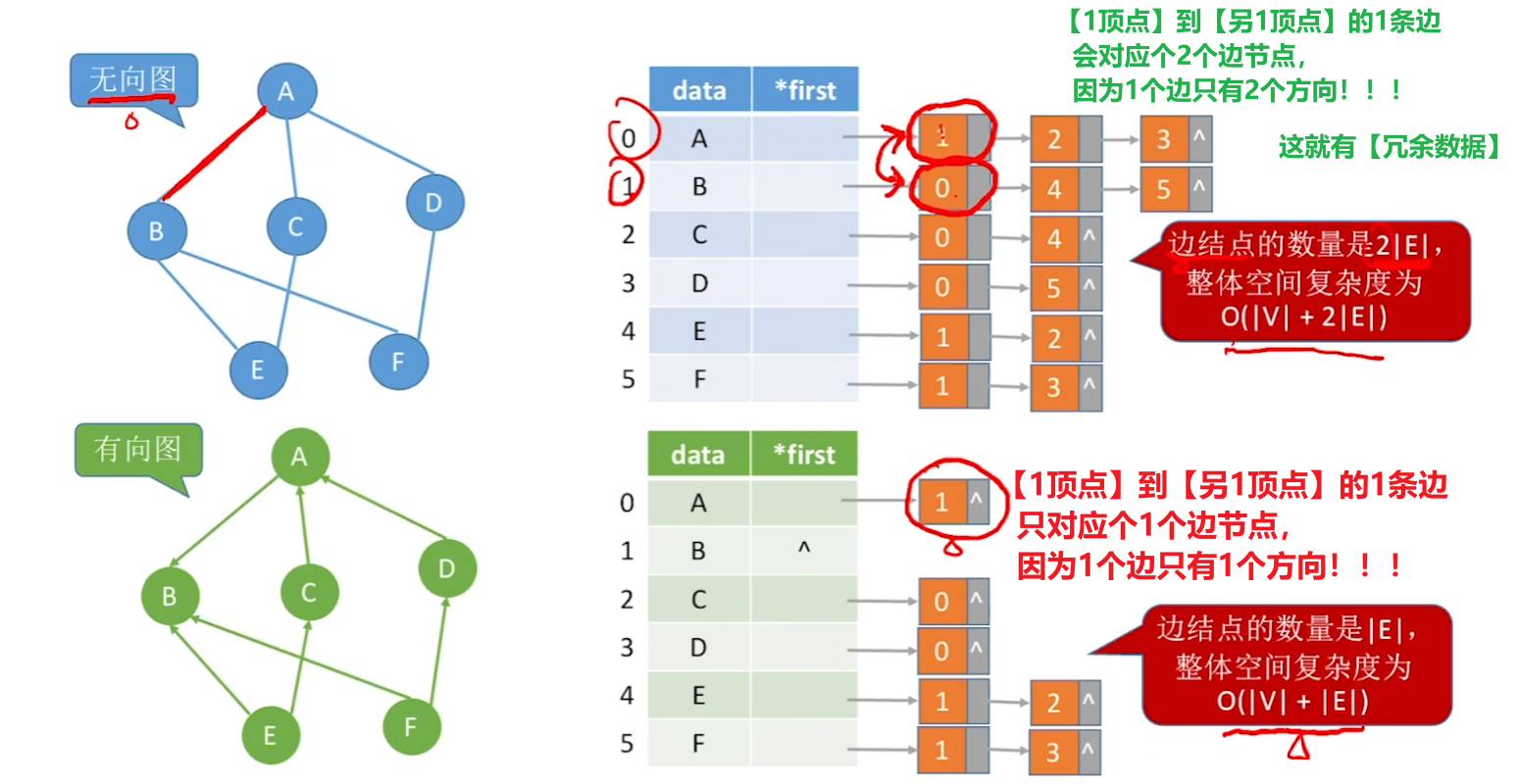
- 2、邻接表的【空间复杂度】:
- 无向图:O(|V| + 2|E|)
- 有向图:O(|V| + |E|)
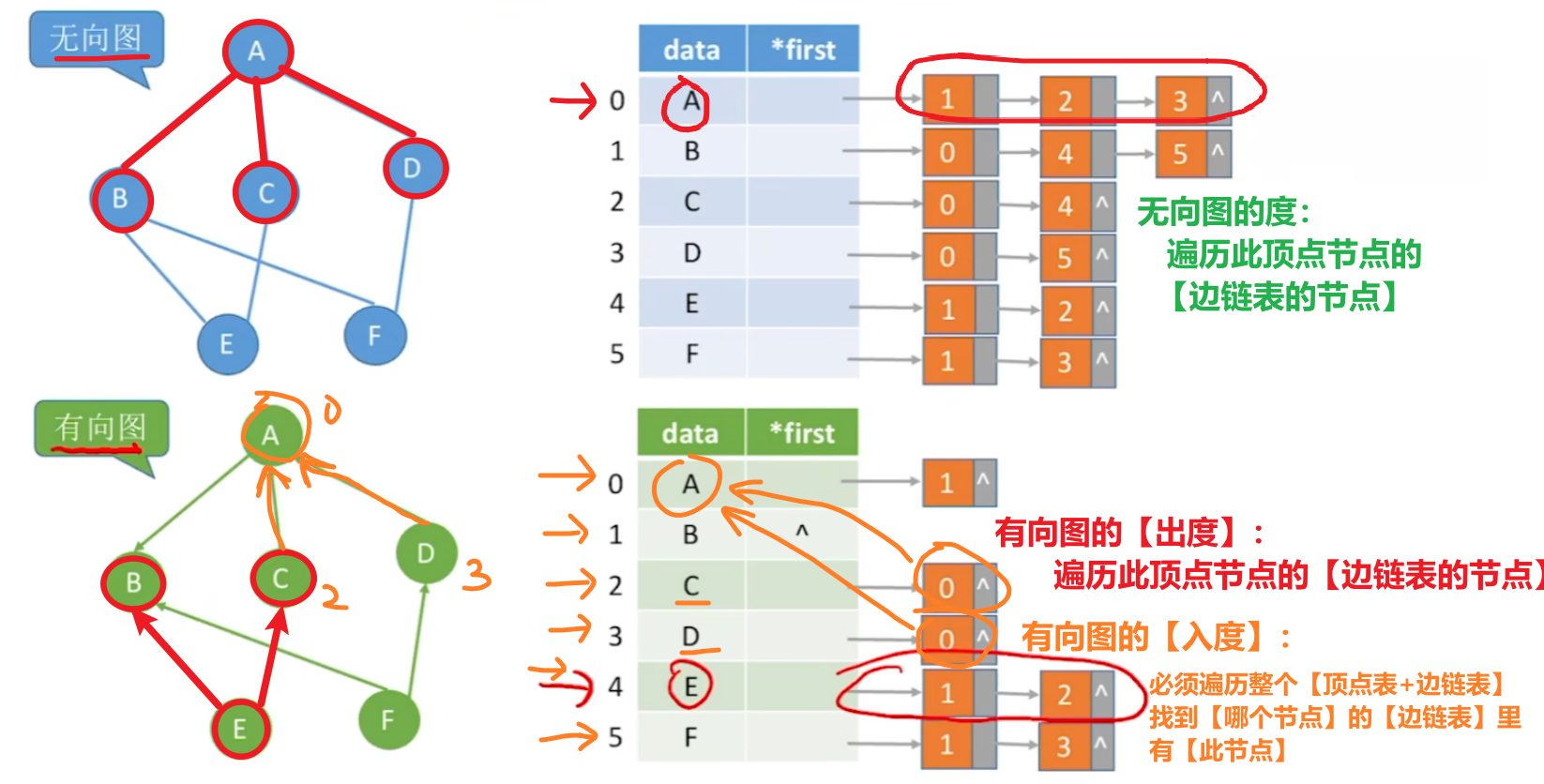
- 3、邻接表【查一个顶点的度】
- 【无向图】:遍历该顶点后的【边链表节点】;
- 【有向图】:
- 【出度】是遍历该顶点的【边链表节点】
- 【入度】是遍历整个【顶点链表】,再把每个节点的【边链表节点】都遍历,找有没有【谁的边节点】是【自己】
- 4、重要!!!
- 【邻接表】表示形式不唯一!!!边链表的节点顺序不唯一!!!
- 【邻接矩阵】表示形式唯一!!!只有一种形式!!!
【记忆特点】
- 邻接表使用的是【链式存储】(单链表)
- 【空间复杂度低】:无向O(|V| + 2|E|)、有向O(|V| + |E|)
- 适合存储【稀疏图】
- 【出度方便】、【入度麻烦】!!!!
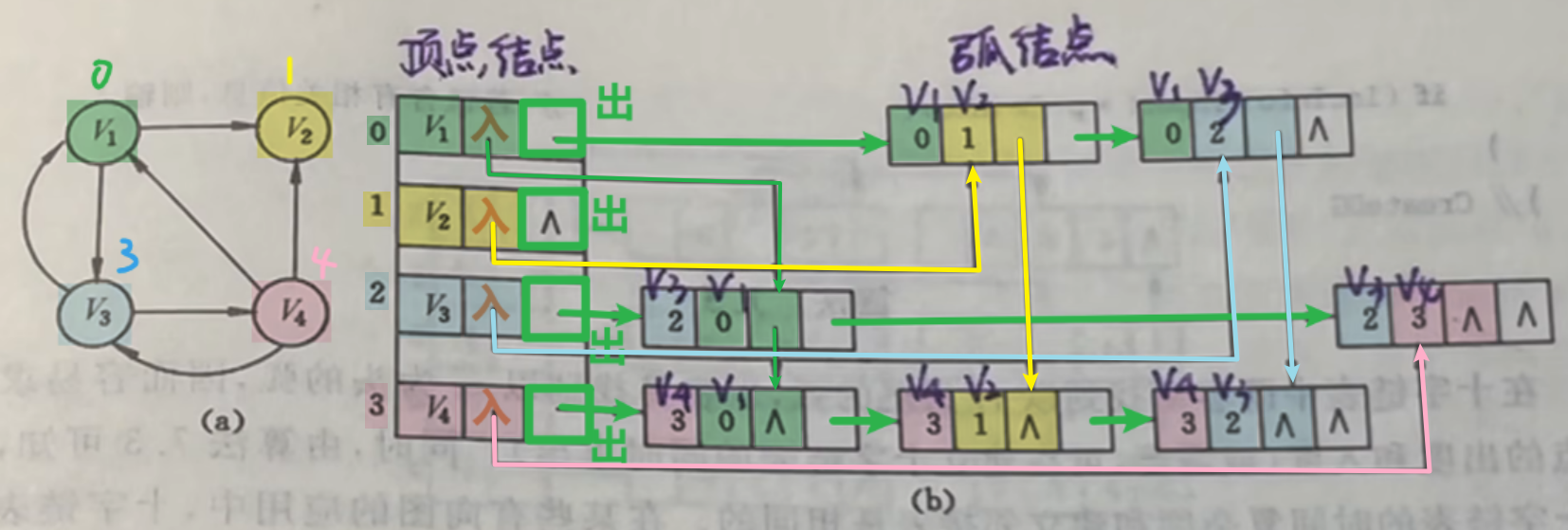
3、十字链表法(不常考,时间紧的可以略看一眼)
【记住】:
- 1、表示的是【有向图】!!!!!!!!!!!!!!
- 2、它的每个顶点节点后面的单链表,指的是【顶点的出弧表】!!!
- 可以发现每个顶点后的【弧链表】每个节点的【头】,都是【此顶点】
- 表示的意思:这就是【这个顶点】的【出度的弧】
- 比如:V1的编号0,他出去的弧有<V1, V2>(0 , 1)、<V1, V3>(0 , 2)
- 3、每个顶点的第二格指【该顶点的入弧】
- 只需要把【弧节点表】的节点里,【第二格】是【该顶点】的全连起来就行
- 比如:图片里我用颜色标注了,同颜色的都连起来了,连这些节点的编号,都是同一顶点
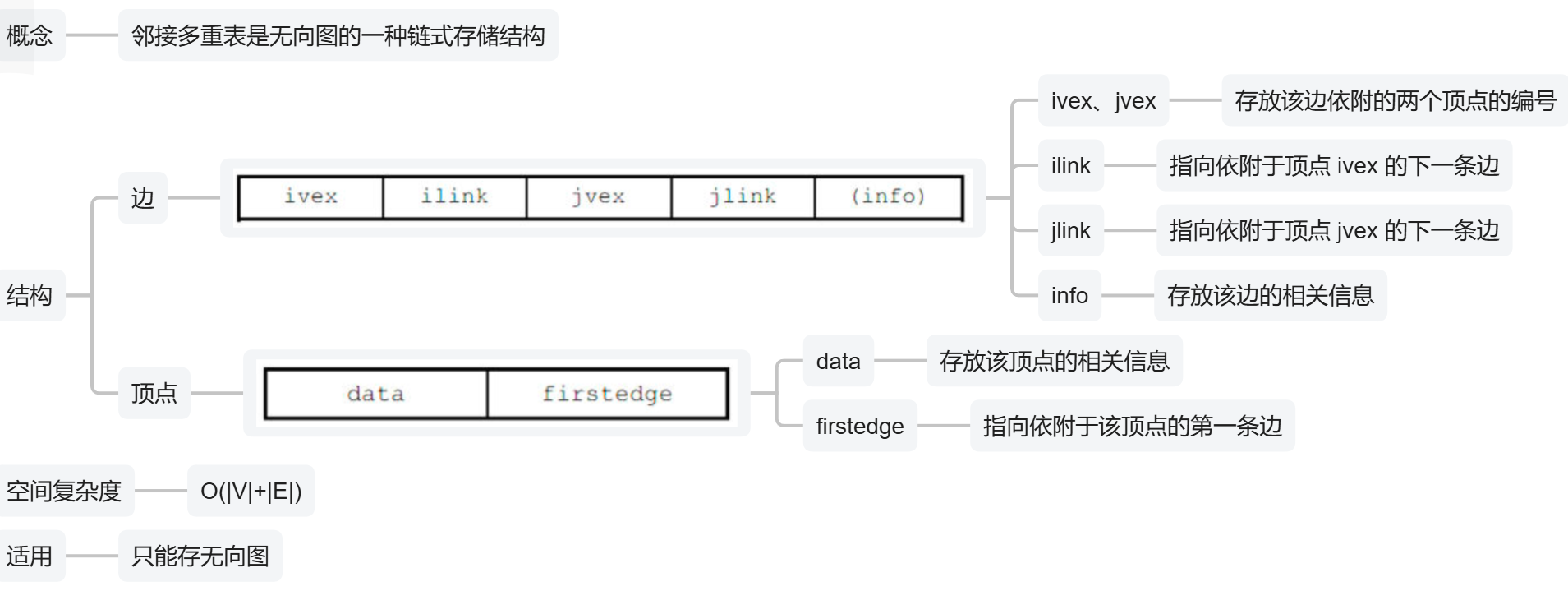
4、邻接多重表法(不常考,时间紧的可以略看一眼)
【记住】:
- 1、表示的是【无向图】!!!!!!!!!!!!!!
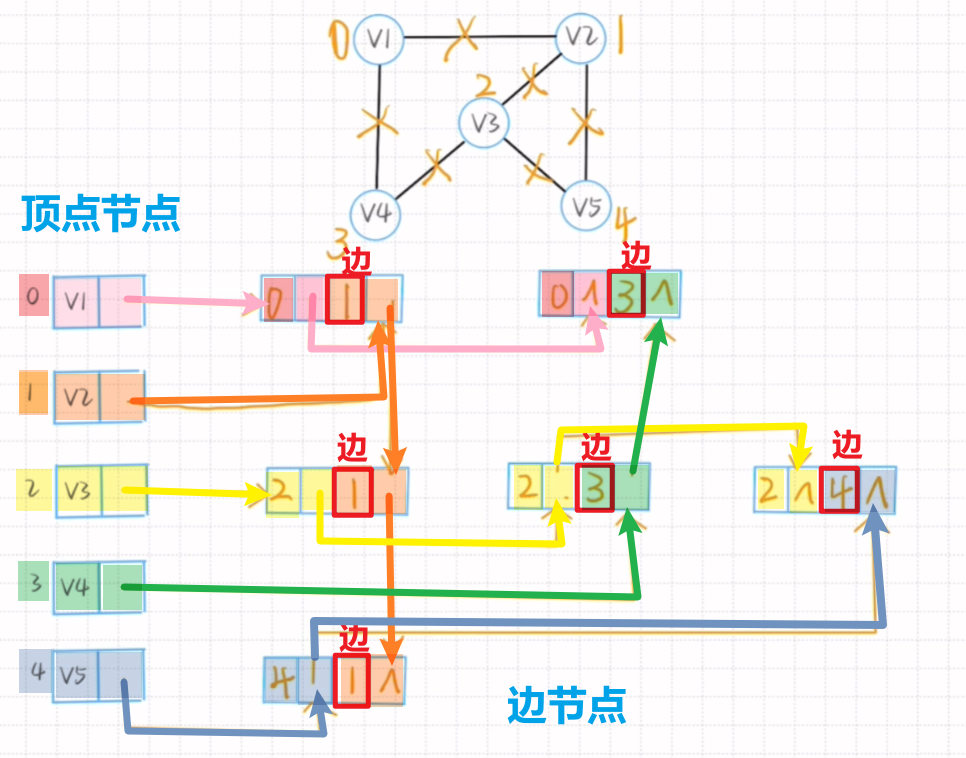
- 2、它的每个顶点节点后面的单链表,指的是【连了该顶点的边】!!!
- 可以发现每个顶点后的【边链表】每个节点的【头】,都是【此顶点】
- 表示的意思:这就是连着【这个顶点】的【边】
- 比如:V1的编号0,他出去的弧有<V1, V2>(0 , 1)、<V1, V4>(0 , 3)
- 3、剩下所有节点的【空格】,只要前面编号一样,都连起来
- 比如:图片里我用颜色标注了,同颜色的都连起来了,连这些节点的编号,都是同一顶点
5、总结(各个存储方式对比)
三、图的操作
理解一下就行,黄色部分记住,大题选择题都会用到
四、图的遍历
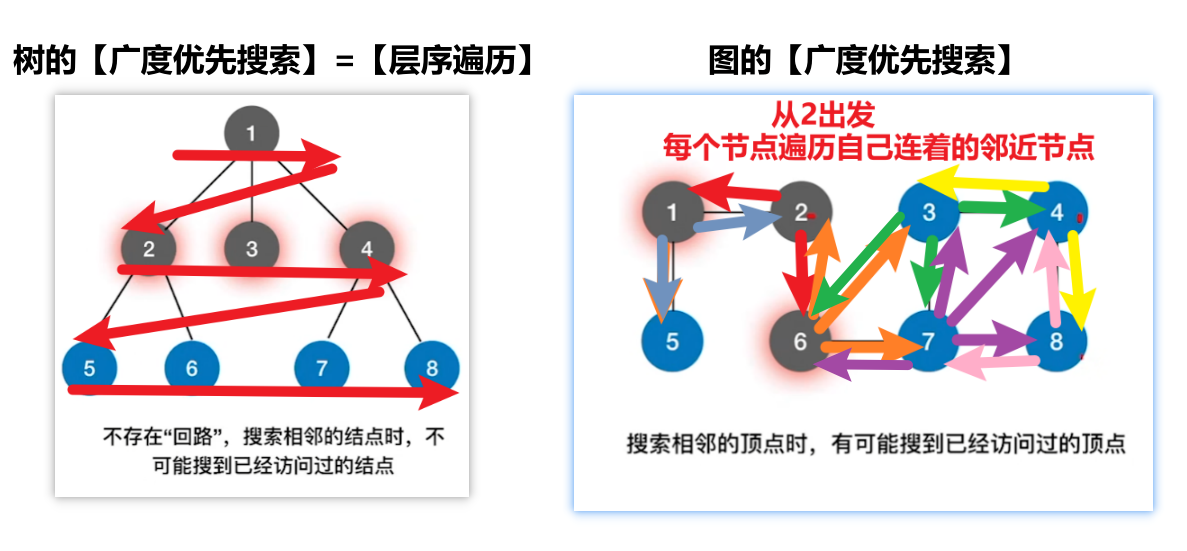
1、广度搜索优先(BFS)
带入【树的层序遍历】来理解【图的广度优先搜索】
就是:每次都把一个顶点的邻近的点都遍历一遍,再到下一个顶点
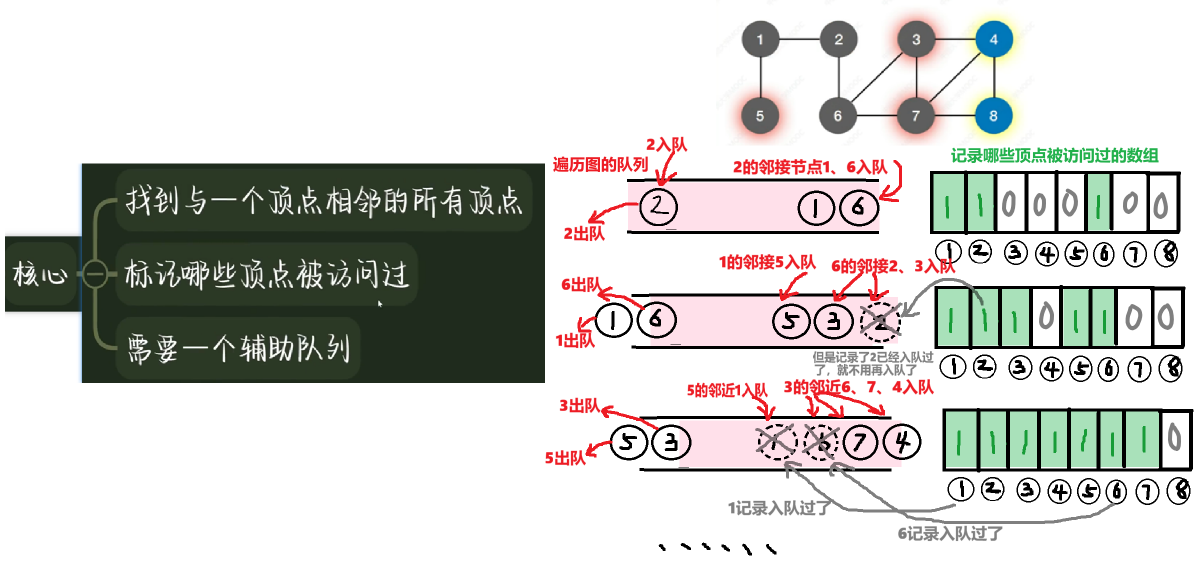
- 1、具体怎么做?核心就三步:(和树层序遍历一样,要借助队列)
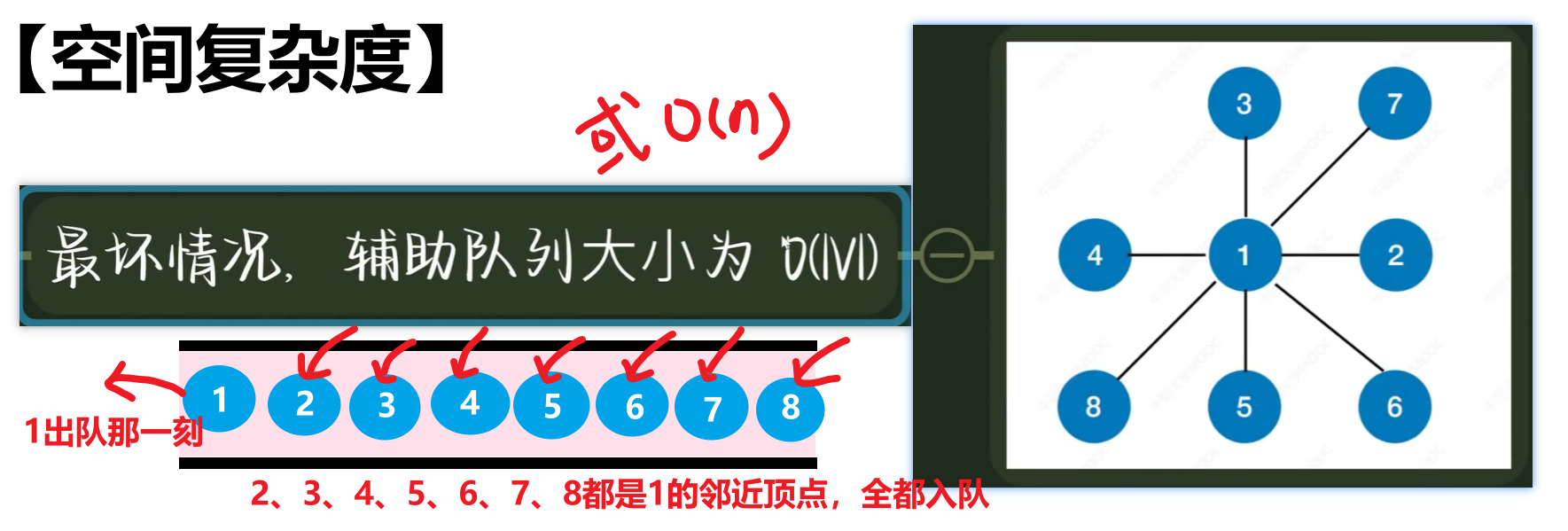
- 2、【空间复杂度】
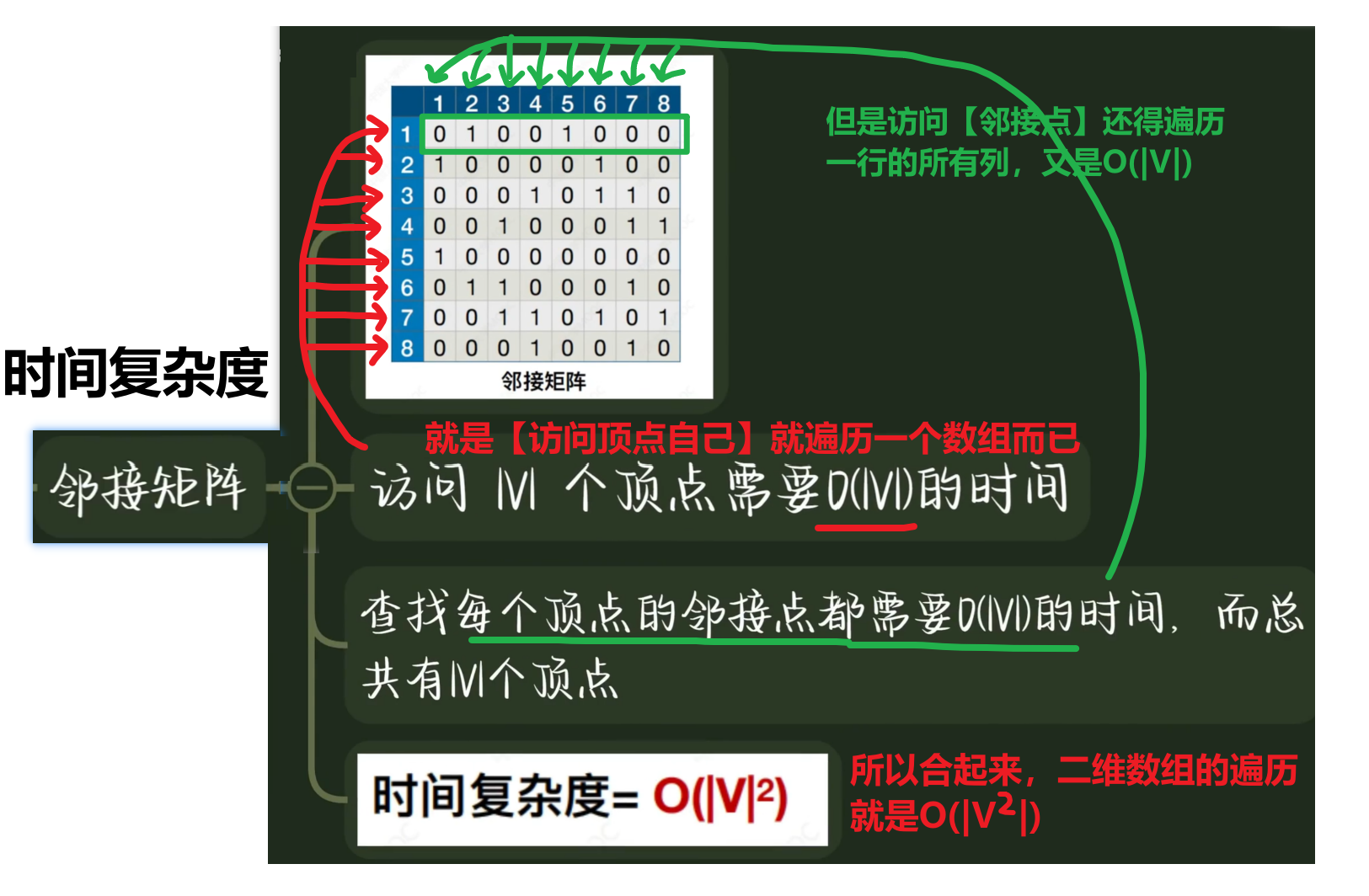
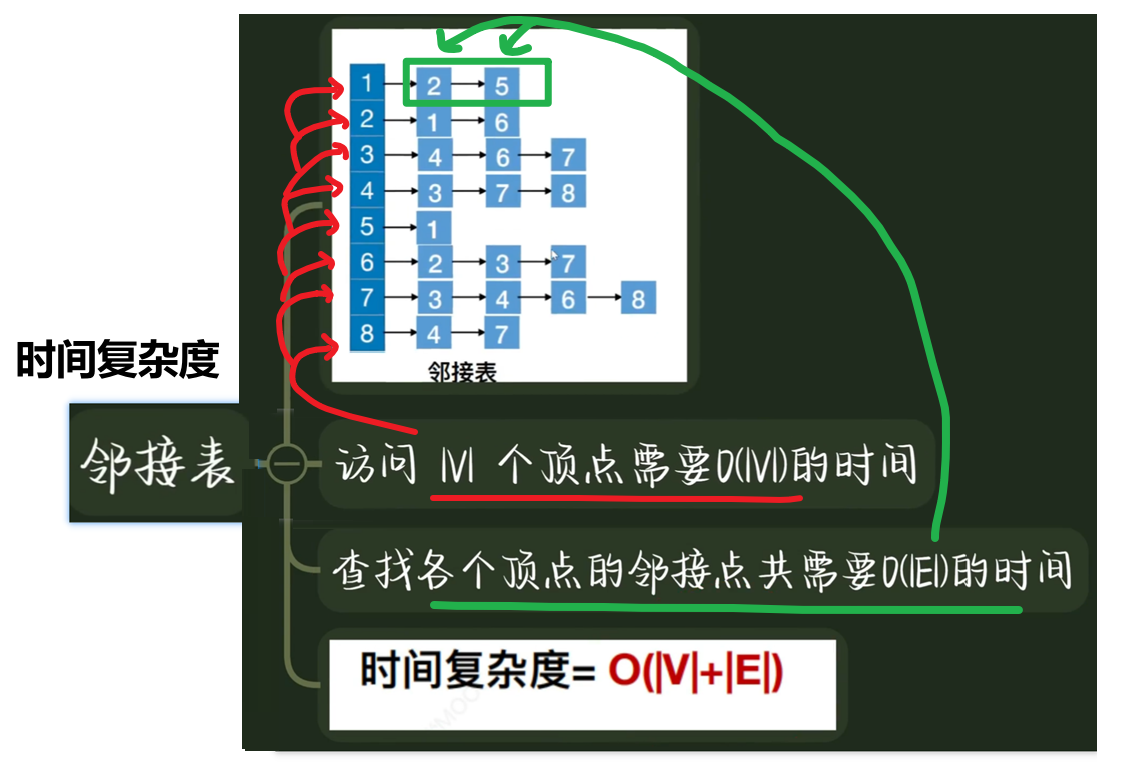
- 3、【时间复杂度】
- 【邻接矩阵】形式存储的【时间复杂度】
- 【邻接表】形式存储的【时间复杂度】
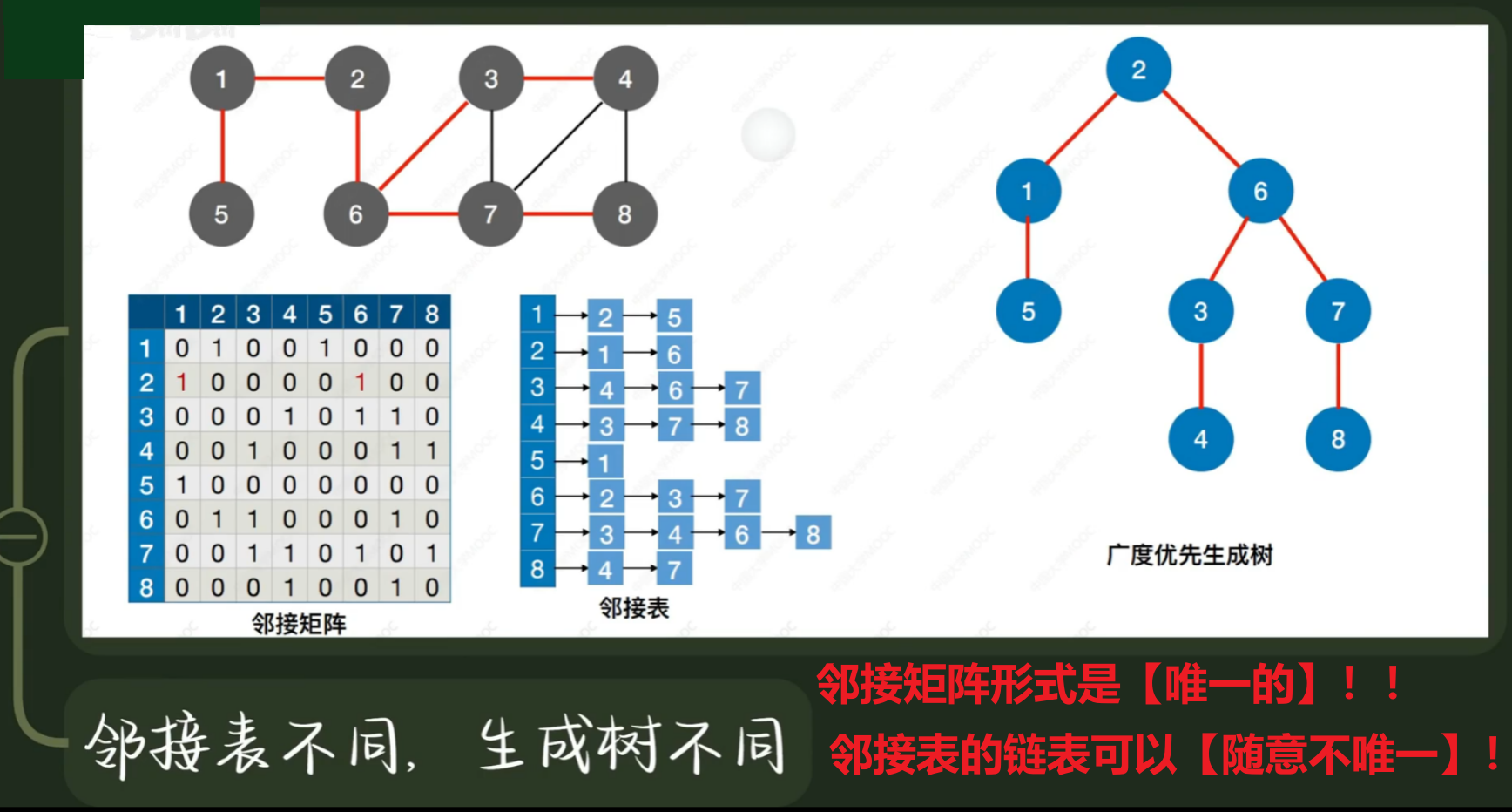
- 4、【广度优先生成树】
- 要记住【邻接矩阵】和【邻接表】两种存储方式的区别,前面讲过的
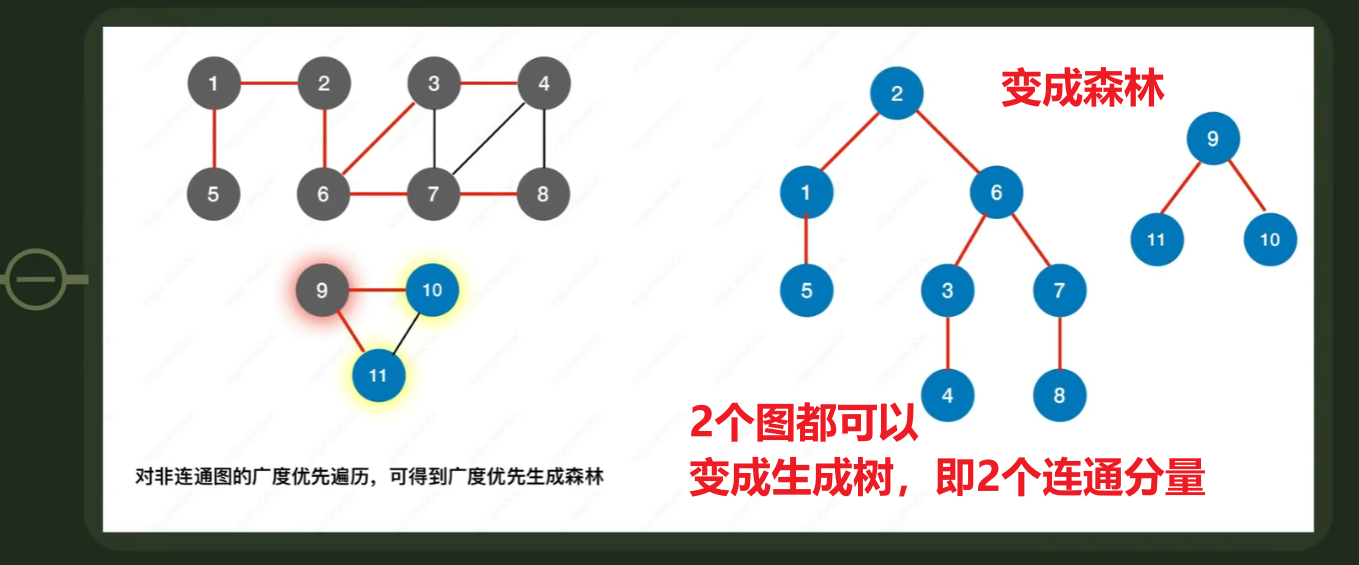
- 5、【广度优先生成森林】
- 简单看一下,理解就行
;
;
【总结】
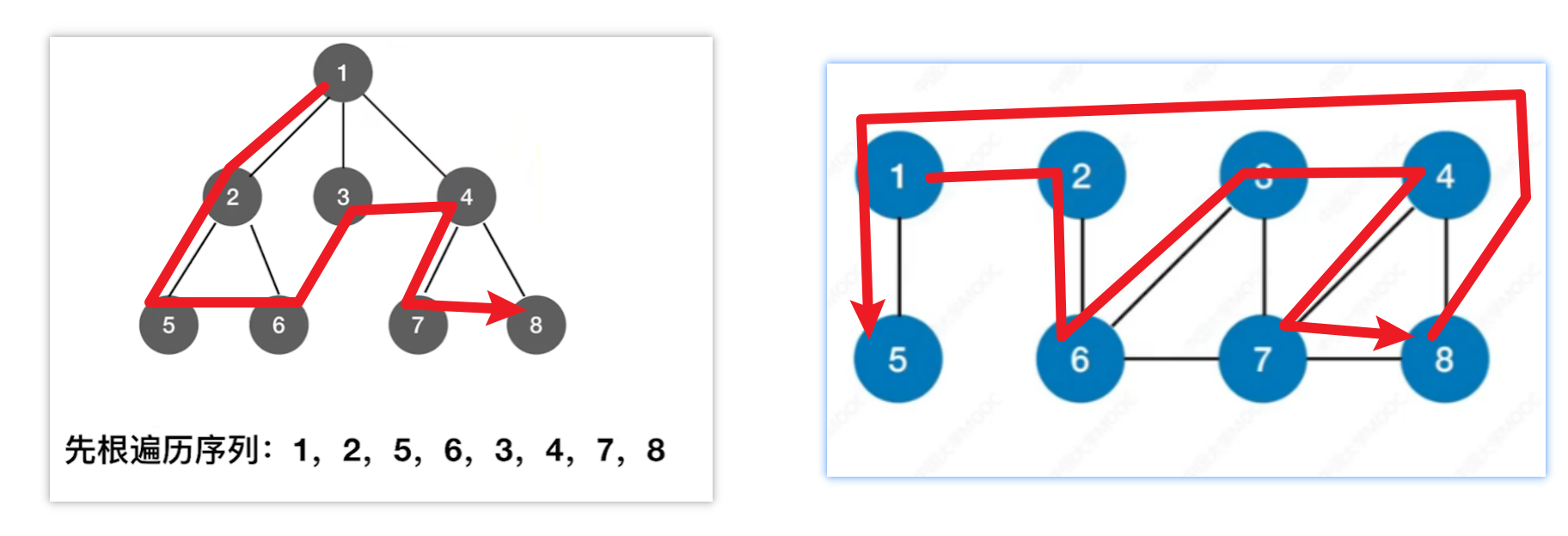
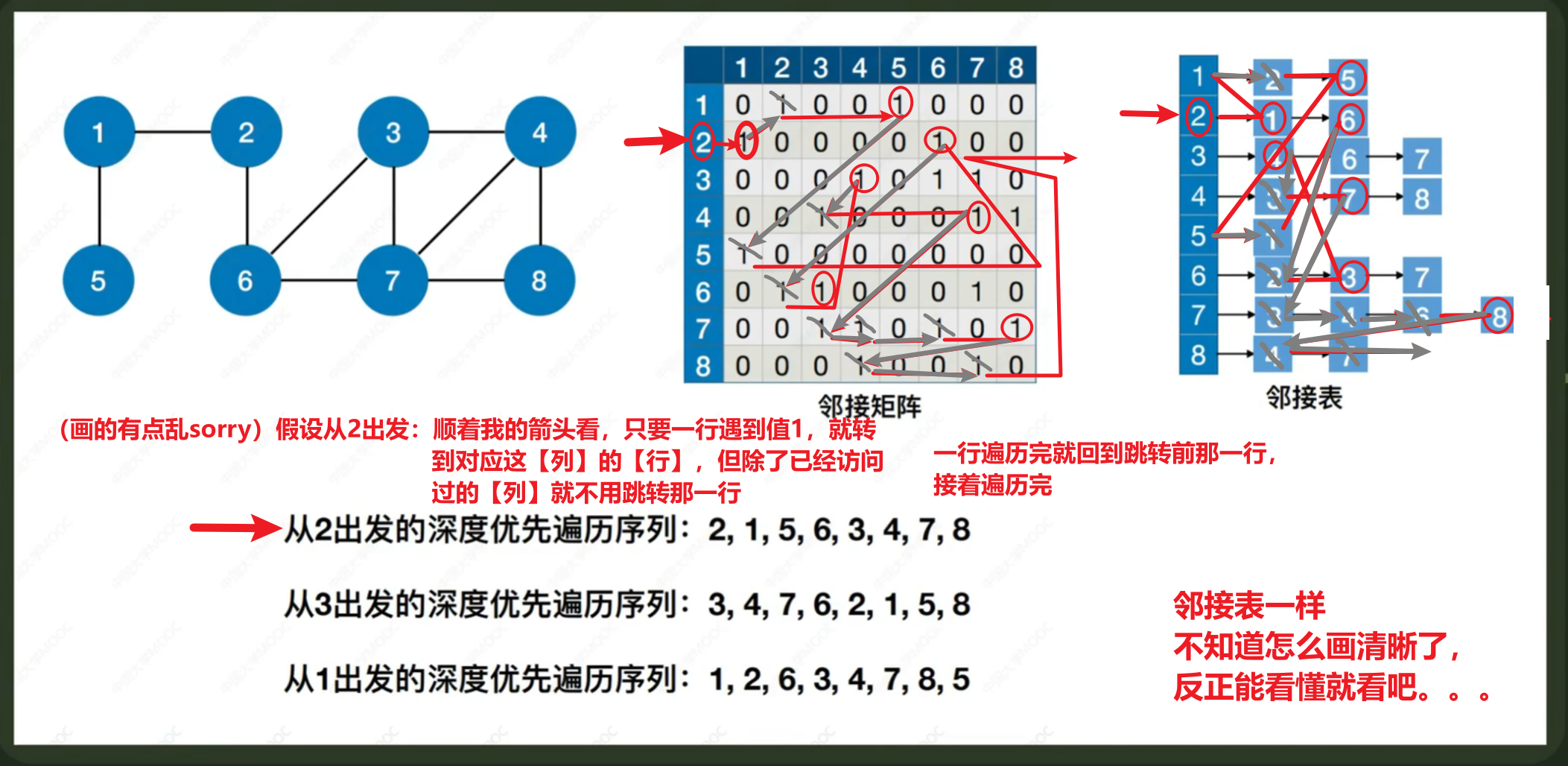
2、深度搜索优先(DFS)
3、图的遍历、图的流通性
类似树的【先根遍历】
未完待续。。。。