[人工智能-大模型-103]：模型层 - M个神经元组成的单层神经网络的本质

前言：

M个神经元组成的单层神经网络的本质：对N维向量空间的信息进行特征提取，并用这些提取出的特征重新构建了一个M维度的向量空间，每个神经元的代表在新的向量空间的一个维度，神经元的输出就是该神经元所在维度的坐标值。

一、M个神经元组成的单层神经网络的本质

以下从数学表达、几何变换、特征空间重构三个层面进一步解析其核心机制，并补充实际案例与直观类比：

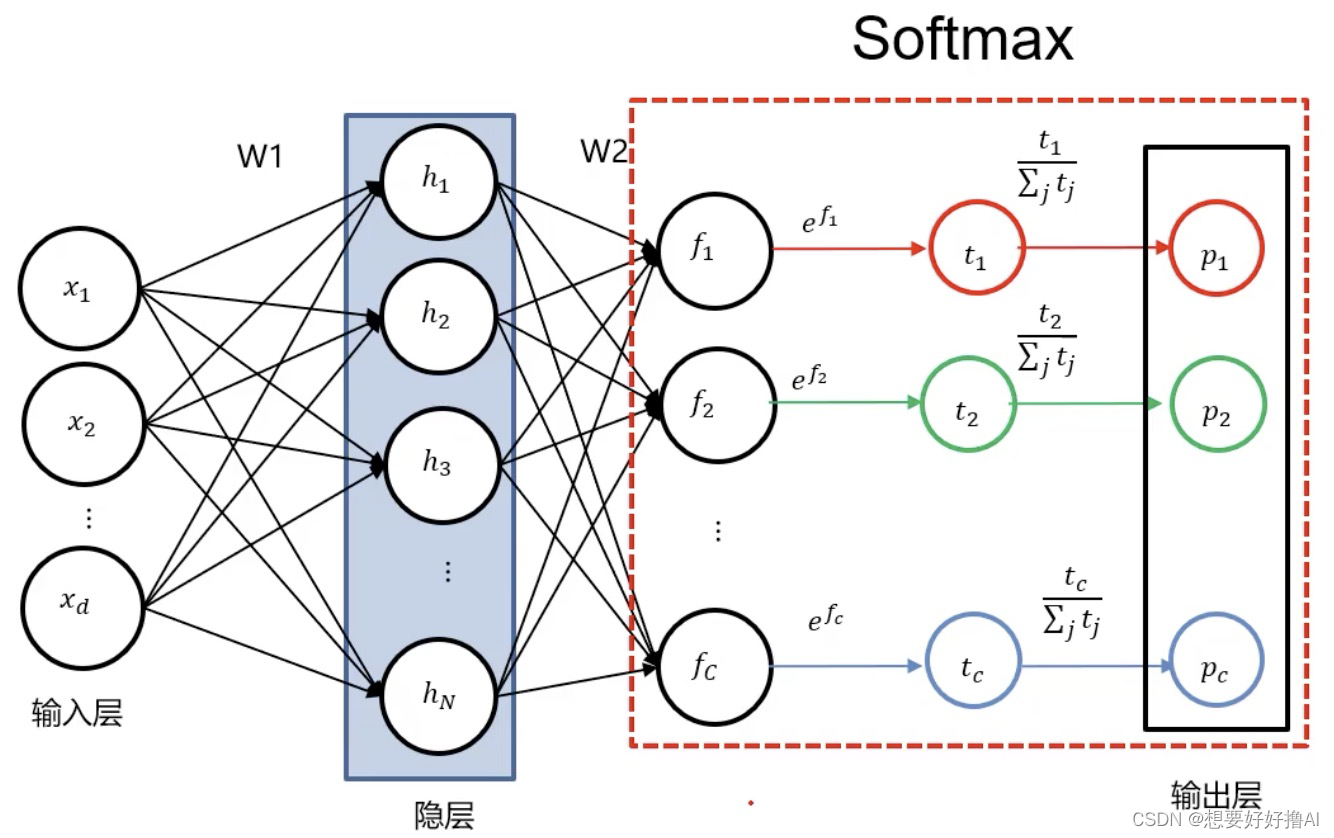
1、数学表达：从输入到输出的线性-非线性映射

2、几何变换：从N维到M维的空间重构

神经元的W，B一旦确定，映射模式就已经确定，不管外部的数据如何变化，映射模式不变。

3、特征空间重构的直观理解

4、实际案例：手写数字识别

5、与深度网络的对比

单层网络的局限性在于其特征提取能力受限：

1. 线性可分性：单层网络只能拟合线性可分的数据（或通过激活函数引入有限非线性）。
2. 深度网络的优势：多层网络通过层级变换逐步构建更复杂的特征（如从边缘→纹理→物体部件→整体），实现高维流形上的非线性分离。

6、总结：单层神经网络的几何本质

这种几何解释不仅揭示了神经网络的工作原理，还为理解模型训练（如权重更新如何调整超平面方向）和泛化能力（如决策边界的平滑性）提供了直观框架。

二、补充信息：向量空间

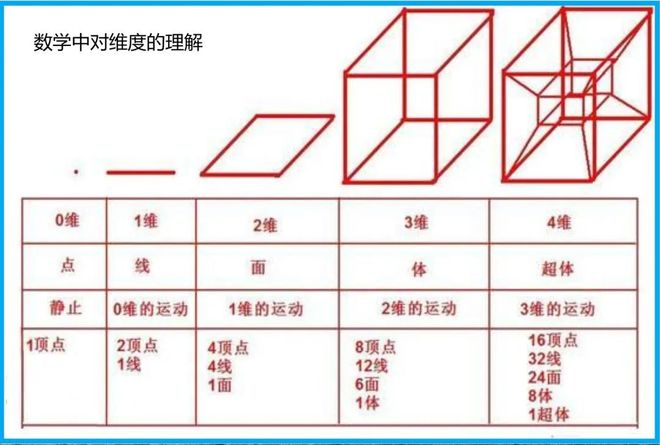
0维：表示静止，用于数值用于不变。只要有变化，就至少是一维。

向量空间（Vector Space），又称线性空间（Linear Space），是数学中用于研究向量及其线性运算（加法和数乘）的核心结构。它为线性代数、函数分析、机器学习等领域提供了基础框架，尤其在描述数据几何关系和变换时至关重要。以下从定义、性质、实例和应用四个层面展开解析：

1、向量空间的定义

向量空间是一个满足以下条件的非空集合 V：

1. 封闭性：
   • 加法封闭：对任意 u,v∈V，有 u+v∈V。
   • 数乘封闭：对任意标量 c∈F（实数域 R 或复数域 C）和 u∈V，有 cu∈V。
2. 存在零向量：存在 0∈V，使得对任意 u∈V，有 u+0=u。
3. 存在负向量：对任意 u∈V，存在 −u∈V，使得 u+(−u)=0。
4. 加法满足八条公理：
   • 结合律、交换律、零元存在性、负元存在性。
5. 数乘满足六条公理：
   • 分配律、结合律、单位元（1u=u）。

直观理解：向量空间是一个“允许自由伸缩和相加”的集合，其中的元素（向量）可以通过线性组合生成新的向量。

2、向量空间的核心性质

1. 基（Basis）与维度（Dimension）：
   • 基：向量空间中的一组线性无关向量，其线性组合能表示空间中的所有向量。
   • 维度：基中向量的个数，记为 dim(V)。例如，R3 的维度为3，基为 {(1,0,0),(0,1,0),(0,0,1)}。
2. 子空间（Subspace）：
   • 向量空间的非空子集，且对加法和数乘封闭。例如，R3 中的平面（二维子空间）和直线（一维子空间）。
3. 线性无关与线性相关：
   • 线性无关：一组向量中，不存在向量可表示为其他向量的线性组合。
   • 线性相关：存在至少一个向量可表示为其他向量的线性组合。
4. 同构（Isomorphism）：
   • 两个维度相同的向量空间可通过线性变换一一对应，结构上等价。

3、向量空间的实例

1. 经典向量空间：
   • Rn：n维实数向量空间，每个向量有n个实数分量。
     • 例如，R2 是平面上的所有点，R3 是三维空间中的所有点。
   • Cn：n维复数向量空间，每个分量是复数。
2. 函数空间：
   • 连续函数空间 C([a,b])：区间 [a,b] 上的所有连续函数，加法和数乘定义为点对点运算。
     • 例如，f(x)=sin(x) 和 g(x)=cos(x) 的线性组合 c1​f+c2​g 仍属于该空间。
   • 多项式空间 Pn​：次数不超过n的多项式集合，基为 {1,x,x2,...,xn}。
3. 矩阵空间：
   • Mm×n​：所有 m×n 矩阵的集合，加法和数乘定义为矩阵对应元素运算。
4. 其他抽象空间：
   • 信号空间：时间序列或图像可视为高维向量。
   • 概率分布空间：满足特定条件的概率密度函数集合。

4、向量空间在机器学习中的应用

1. 数据表示：
   • 输入数据（如图像、文本）通常表示为向量空间中的点。例如：
     • 图像：展平为像素向量（如 28×28 图像→784维向量）。
     • 文本：词嵌入（如Word2Vec将单词映射为300维向量）。
     • 视觉（动画）图像信息的维度要远大于文字的信息。
2. 特征提取：
   • 神经网络通过线性变换（全连接层）和激活函数将数据映射到新的向量空间，提取更高阶特征。
   • 例如，卷积神经网络（CNN）将图像映射到特征图空间，每个神经元代表的通道代表一种局部模式。
3. 降维与可视化：
   • 主成分分析（PCA）通过寻找数据的主方向（基向量）将高维数据投影到低维空间。
   • t-SNE、UMAP等算法将数据映射到二维/三维空间，便于可视化聚类结构。
4. 距离与相似度：
   • 向量空间中的距离（如欧氏距离、余弦相似度）用于衡量数据点的相似性。
   • 例如，推荐系统中通过计算用户/物品向量的余弦相似度进行推荐。

5、几何直观：向量空间的“空间”含义

1. 几何结构：
   • 向量空间中的向量可视为有方向和长度的箭头，加法对应平行四边形法则，数乘对应缩放。
   • 例如，R2 中的向量 (2,3) 可表示为从原点指向点 (2,3) 的箭头。
2. 子空间的几何意义：
   • 一维子空间：通过原点的直线。
   • 二维子空间：通过原点的平面。
   • 高维子空间：无法直接可视化，但可通过投影理解。
3. 线性变换的几何效果：
   • 矩阵乘法对应向量空间的旋转、缩放、剪切等变换。
   • 例如，旋转矩阵将向量绕原点旋转特定角度。

6、总结：向量空间的核心价值

向量空间为数据和运算提供了统一的数学框架，其核心价值在于：

1. 抽象性：统一处理不同类型的数据（如数值、函数、矩阵）。
2. 线性运算：通过加法和数乘描述数据变换和组合。
3. 几何解释：为算法提供直观的空间视角（如分类边界、聚类结构）。
4. 理论基础：支撑线性代数、泛函分析等数学工具，进而支持机器学习模型的优化与泛化分析。

理解向量空间是掌握线性模型、神经网络和降维技术的关键，它帮助我们从“数据点”的视角上升到“空间结构”的视角，揭示数据背后的几何规律。