Java二分算法题目练习

二分查找

题目解析：在一个有序数组中找一个target ，找到返回其下标，找不到返回-1
算法原理：1.暴力解法：遍历整个数组进行查找时间复杂度O(N)
2.朴素二分算法：我们可以发现其数组是可以根据一个值将其分为两部分并且可以比较然后舍弃一部分，此时这个数组具有“二段性”，因此可以使用二分算法

class Solution {public int search(int[] nums, int target) {//此时就用left和right两个变量在左右两边//使用mid来表示其中间的下标，因为其有序//这样我们每次比较一次其就会干掉一半的数这个效率是很高的int left = 0;int right = nums.length - 1;while(left <= right){int mid = left + (right - left) / 2;//防溢出if(target > nums[mid]){//在[mid+1 , right]left = mid + 1;}else if(target < nums[mid]){//在[left,mid - 1]right = mid - 1;}else{return mid;}}return -1;}
}

时间复杂度：O(log N )
空间复杂度：O(1)

在排序数组中查找元素的第一个和最后一个位置

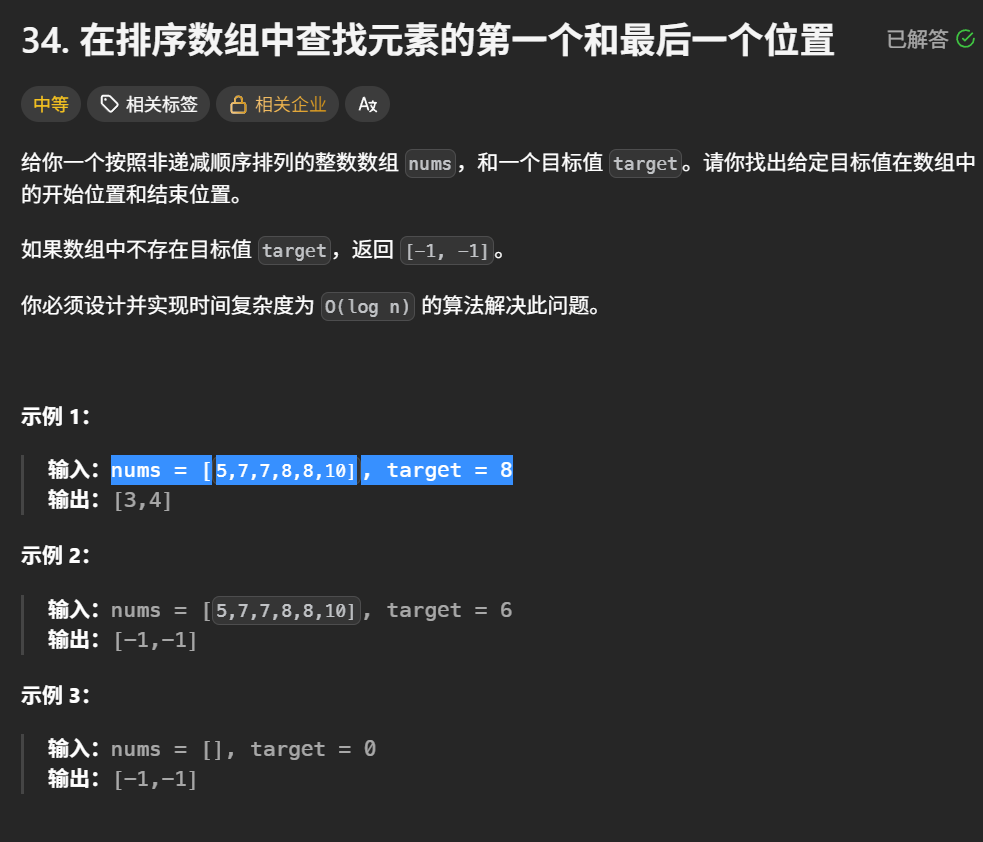
题目解析：就是给了我们一个target，让我们在一个非递减的数组中找其开始和结束下标，并返回，如果找不到就返回[-1,-1]
解法一：暴力解法 ，时间复杂度O(N)
解法二：朴素二分查找，由于我们不确定找的数是其开始和结束位置，因此有可能全部遍历，因此时间复杂度是O(N)
解法三：左右二分算法

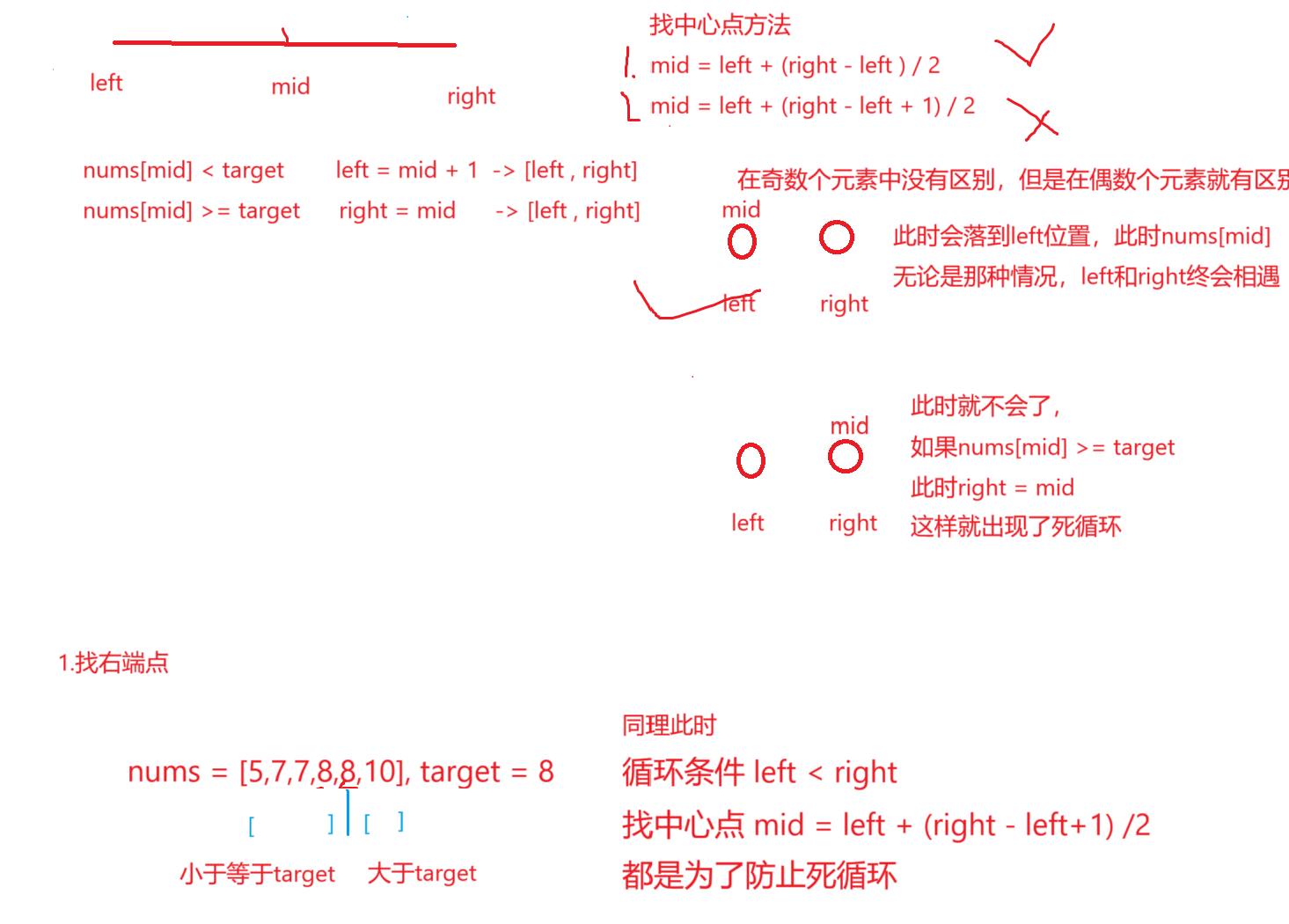
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[2];ret[0] = ret[1] = -1;if(nums.length == 0){return ret;}int left = 0;int right = nums.length - 1;//先左边二分while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < target){left = mid + 1;}else{right = mid;}}//此时left与right相遇就会结束if(nums[left] != target){return ret;}//反之就找到了左端点ret[0] = left;left = 0;//可以不用重置，因此此时上面left对应就是其开始位置right = nums.length - 1;while(left < right){int mid = left + (right - left + 1)/2;if(nums[mid] > target){right = mid - 1;}else{left = mid;}}ret[1] = right;return ret;}
}

x的平方根

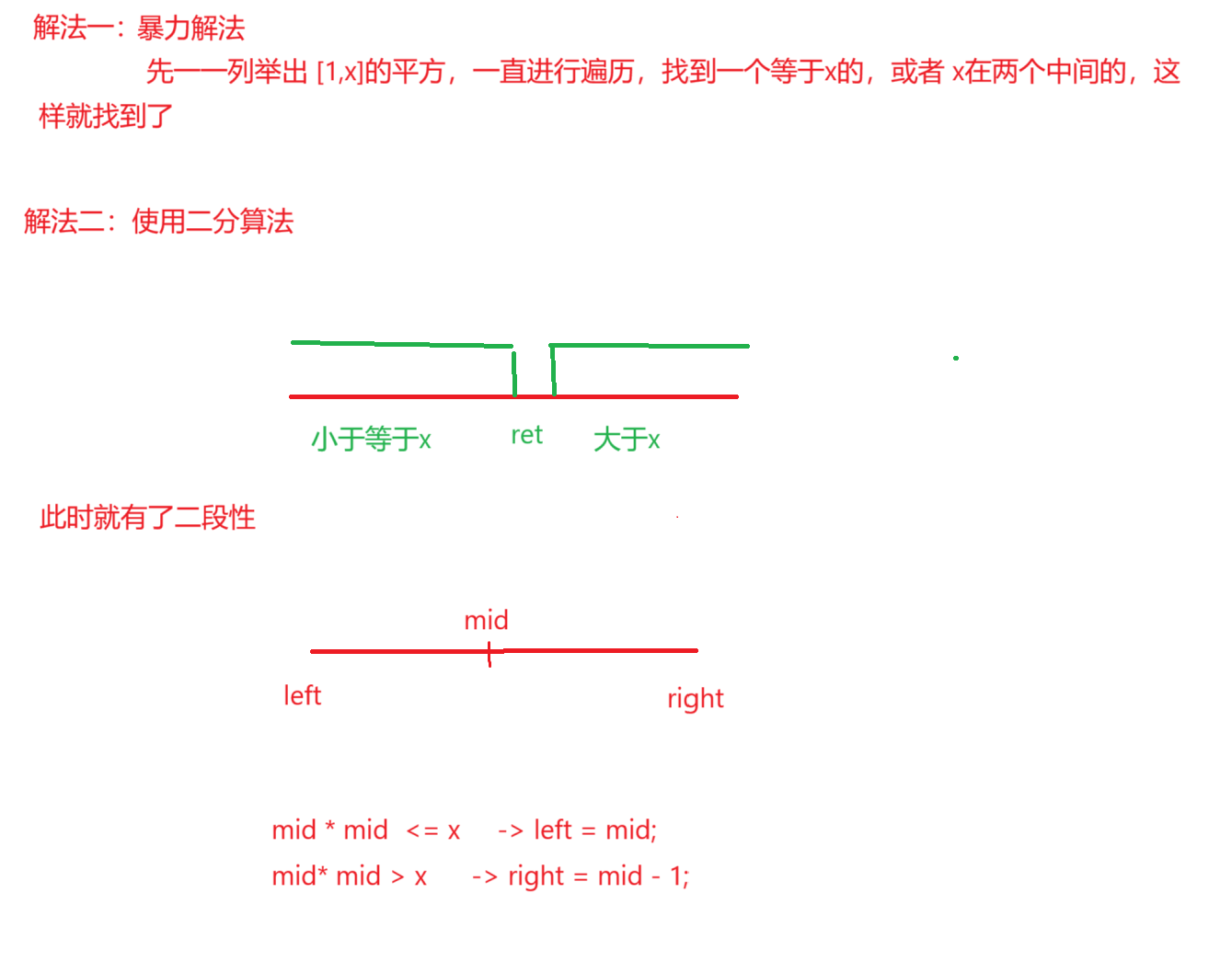
class Solution {public int mySqrt(int x) {//此时如果x<1，此时只保留整数，就是0if(x < 1){return 0;}//防止数据超出long left = 1;long right = x;while(left < right){long mid = left + (right - left + 1) / 2;if(mid * mid <= x){left = mid;}else{right = mid - 1;}}return (int)left;}
}

搜索插入位置

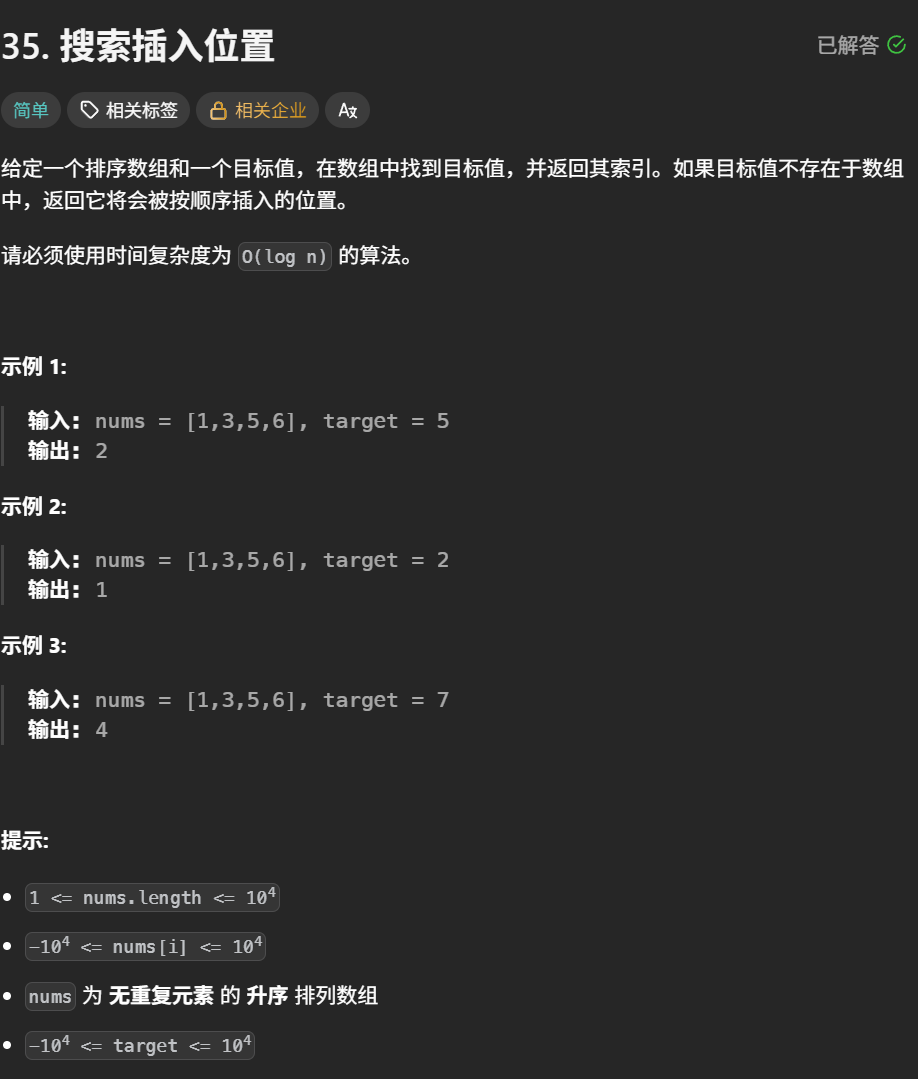
题目解析：在一个无重复元素的升序数组中找出其目标值的位置，但是可能不存在，不存在的话就返回其按顺序插入的位置
二分算法：因为其可以将其数组分为>= target和<target的两部分，并且可以舍弃<target这个部分，因此使用二分算法，并且还是当left 等于 right结束

class Solution {public int searchInsert(int[] nums, int target) {//使用二分算法int left = 0;int right = nums.length - 1;while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target){left = mid + 1;}else{right = mid;}}//注意此时可能从头到尾都是< targetreturn nums[right] < target ? right + 1 : right;}
}

山脉数组的峰顶索引

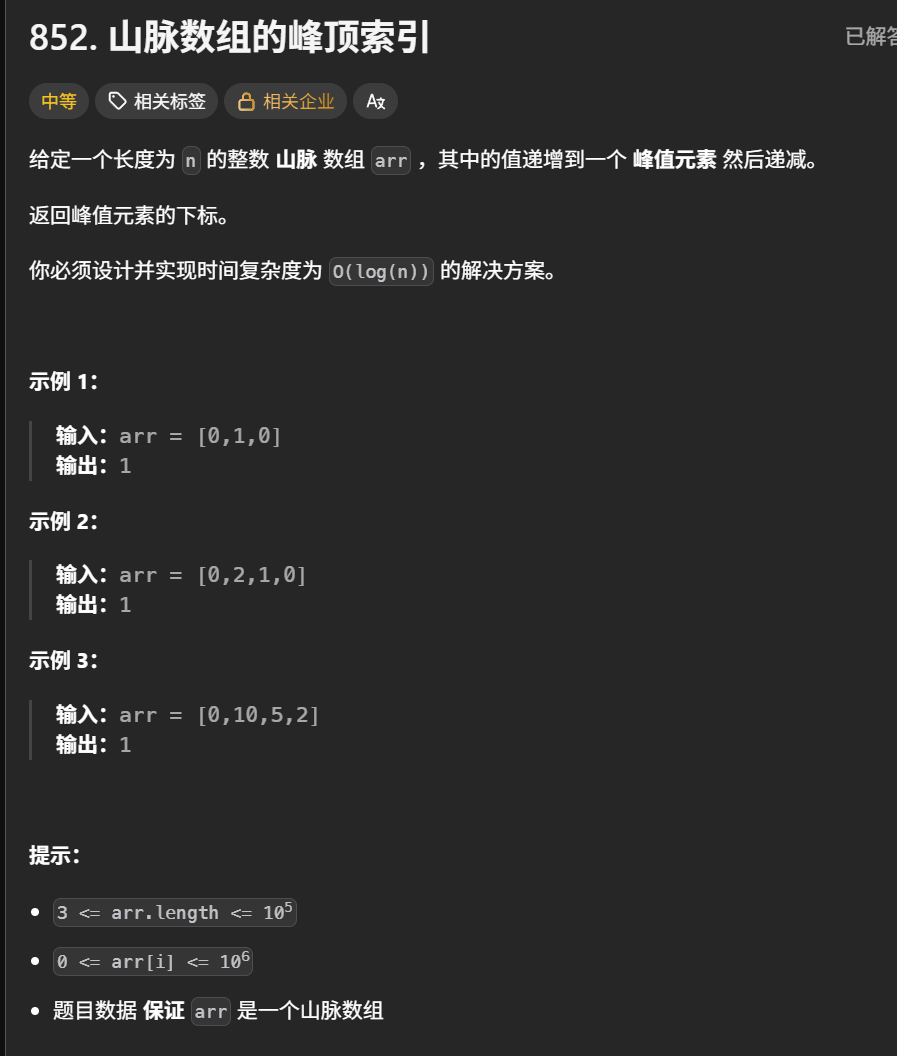
题目解析：在一个一边递增，另一边递减的数组中找出其最大值
因此只需要找出其递增和递减中间的值下标就可以

class Solution {public int peakIndexInMountainArray(int[] arr) {//因为其山脉我们呢可以分为两部分//峰值左边是递增的//峰值右边是递减的int left = 0;int right = arr.length - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid - 1] < arr[mid]){left = mid;}else{right = mid - 1;}}return left;}
}

寻找峰值

题目解析：在一个数组中，找其峰值，并且可能有多个，只需返回任意一个就行
二分算法：因为其是必然有峰值的，并且是不存在两个元素相同，因此其会出现两种情况，要么是递增，要么递减，因此按照分类使用二分算法

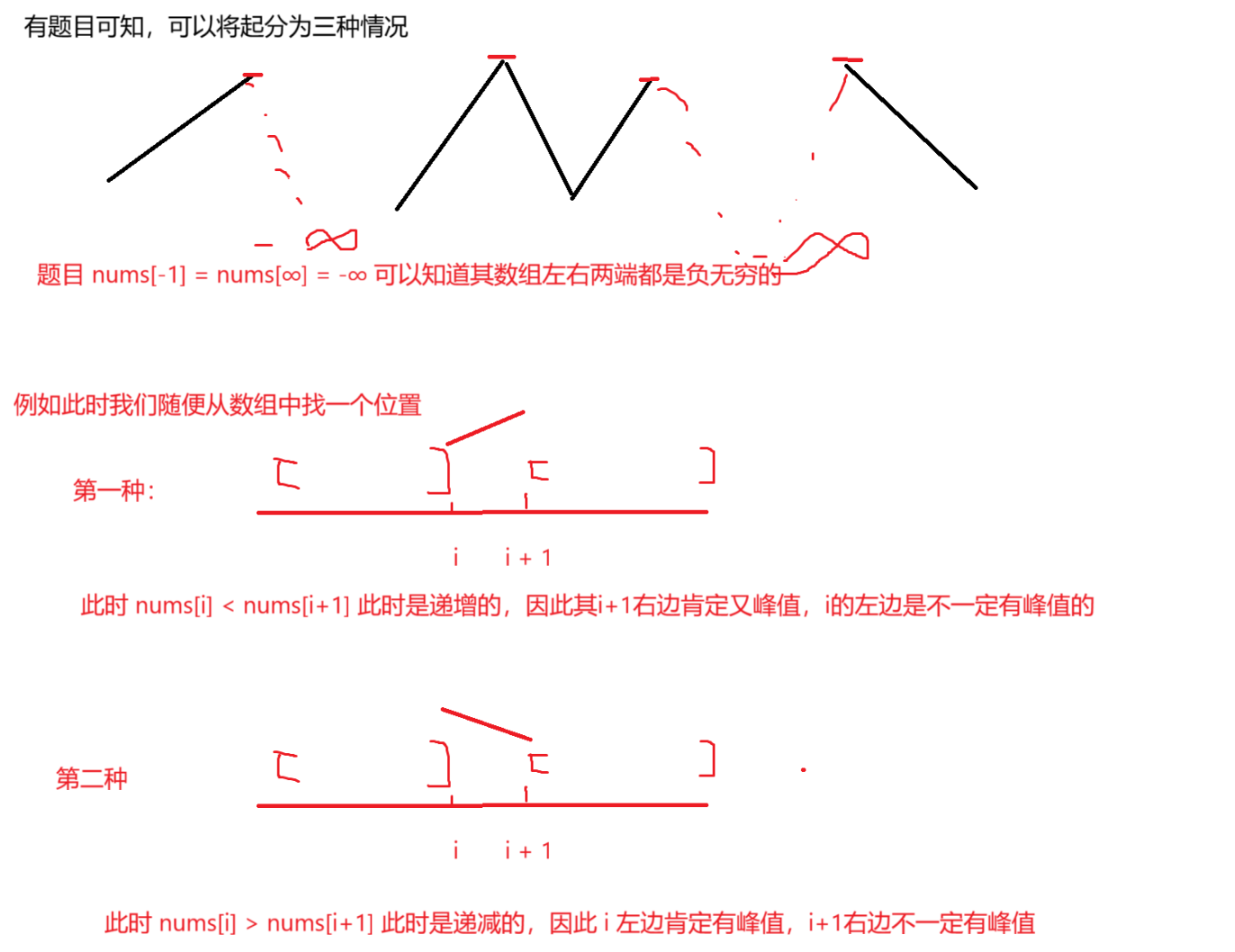
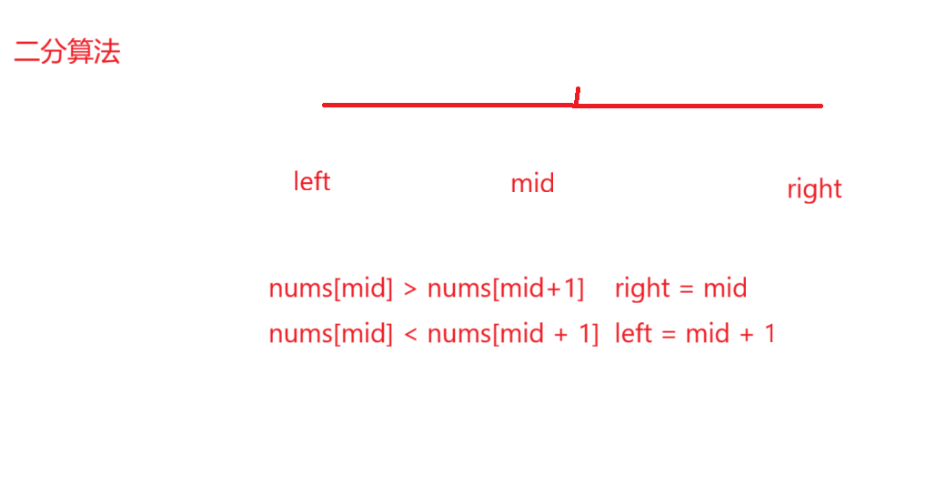
class Solution {public int findPeakElement(int[] nums) {int left = 0;int right = nums.length - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[mid+1]){right = mid;}else{left = mid + 1;}}return left;}
}

寻找旋转排序数组中的最小值

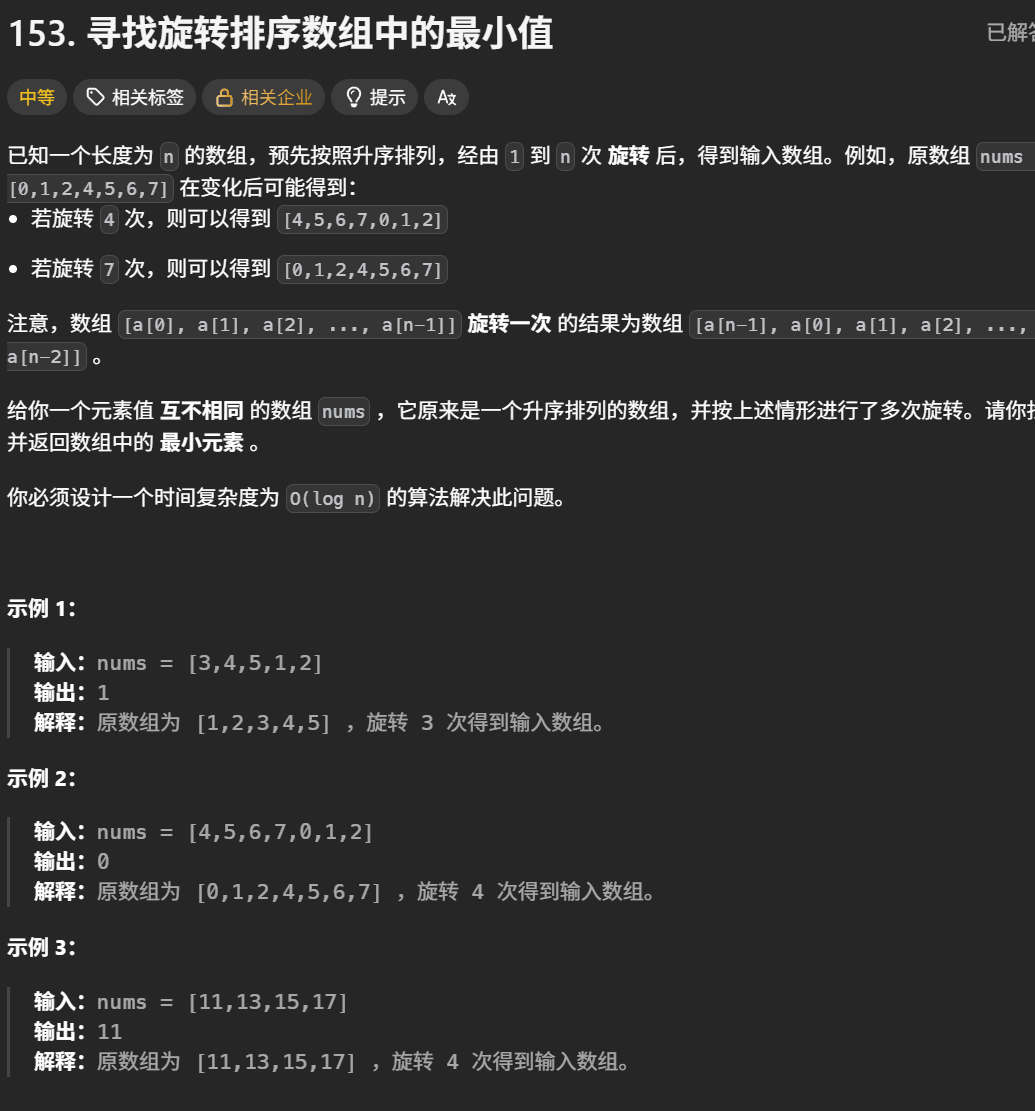
题目解析：原本一个自增的数组，经过旋转，让我们找出其最小的值
算法原理：暴力解法：直接遍历找最小值
二分算法：我们可以以最后一个下标的值为基准值，因此数组可以分为两个部分，一半是>nums[n-1]，一半是 <= nums[n - 1]，就这样根据二段性就可以使用二分算法\

class Solution {public int findMin(int[] nums) {int right  =  nums.length - 1;int n = right;int left = 0;while(left < right){int mid = left +  (right - left)/2;if(nums[mid] > nums[n]){left = mid + 1;}else{right = mid;}}return nums[left];}
}

点名

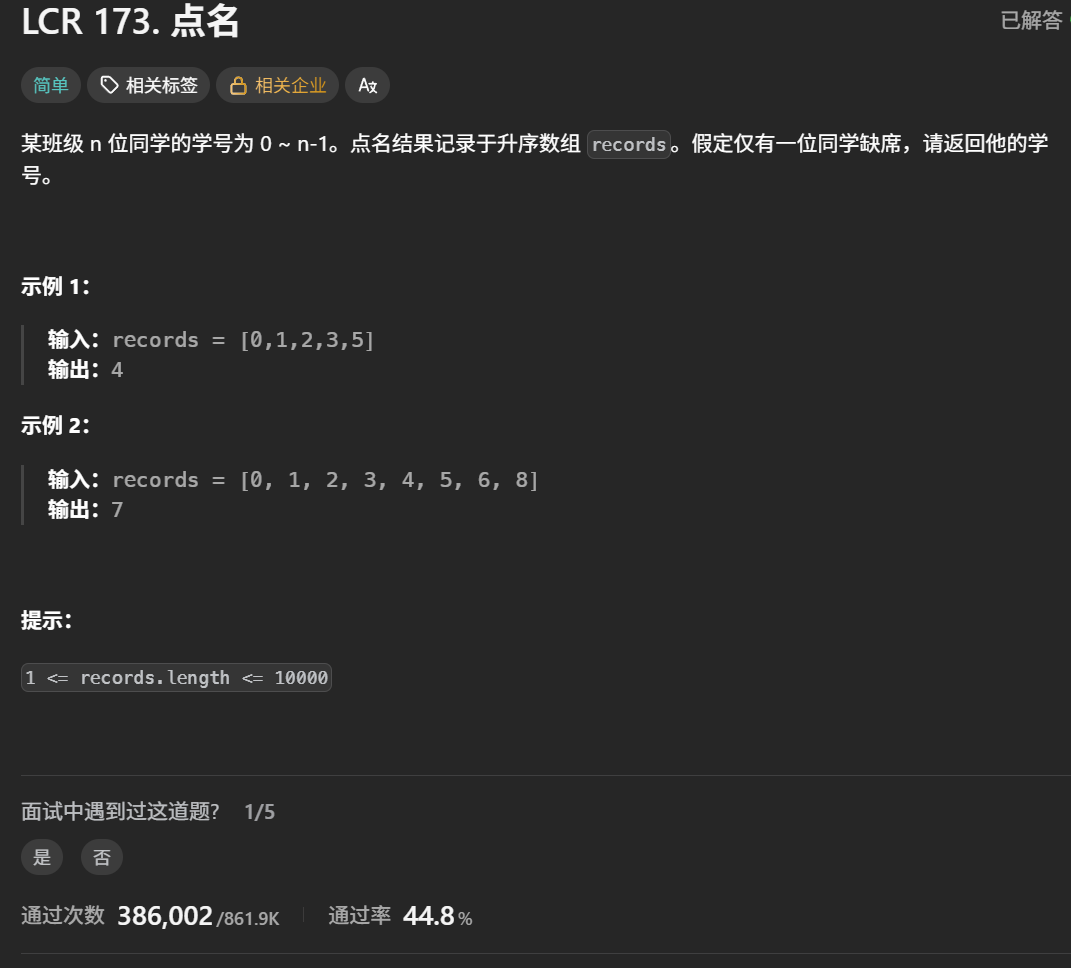
题目解析：就是一个递增的数组，并且其下标和其对应的值是对应的，中间缺了一个数导致其不对应了，我们要找到这个数

//哈希
class Solution {public int takeAttendance(int[] records) {//使用hashSet<Integer> set = new HashSet<>();for(int record : records){set.add(record);}//先全部将其放入hash中，让后一个一个判断其是否在其中就行int len = records.length;for(int i = 0 ; i < len;i++){if(!set.contains(i)){return i;}}//缺少最后一个return len;}
}

//直接遍历
class Solution {public int takeAttendance(int[] records) {//直接遍历for(int i = 0;i < records.length;i++){if(records[i] != i){return i;}}return records.length;}
}

//求和
class Solution {public int takeAttendance(int[] records) {//使用求和方式也可以int len = records.length;int sum = len * (len + 1)/2;for(int i = 0;i < len ;i++){sum -= records[i];}return sum;}
}

//位运算
class Solution {public int takeAttendance(int[] records) {//使用位运算符^int ret = 0;for(int i = 0;i <records.length; i++){ret ^= records[i] ^ i;//此时最后一个下标没有异或}return ret^records.length;}
}

//二分算法
class Solution {public int takeAttendance(int[] records) {//此时就可以将其数字分为两个部分//一部分是其值和下标一样//另一部分是不一样int left = 0;int right = records.length - 1;while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid){left = mid + 1;}else{right = mid;}}return records[left] == left ? left + 1 : left;}
}