三维重建【0-C】3D Gaussian Splatting：相机标定原理与步骤

接上篇 三维重建【0-B】3D Gaussian Splatting：相机标定原理与步骤内容，继续对相机标定原理与步骤进行阐述，本节主要是张氏标定法的初步讲解与单应性矩阵的推导计算。

一、相机标定的目的

给定物体的参考点坐标(x, y, z)和它的像素坐标(u, v)，从而确定相机内部的几何和光学特性（内部参数）、摄像机在三维世界坐标关系（外部参数）。

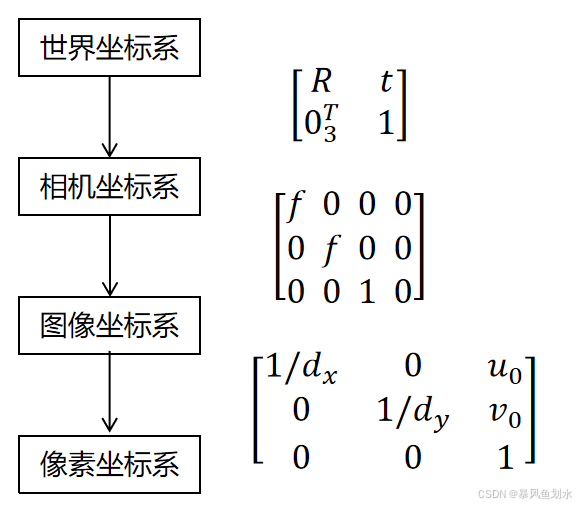
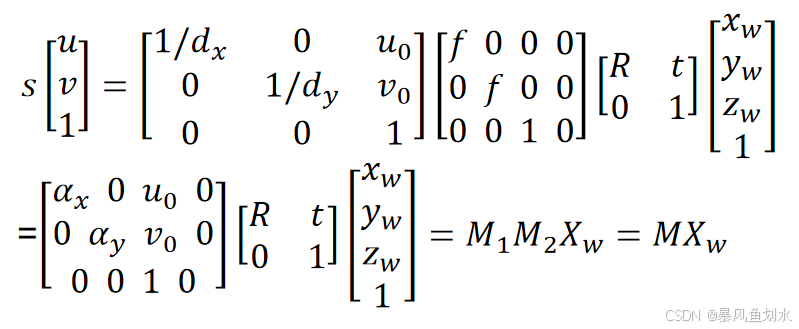
二、标定方法分类

• 传统的摄像机标定方法
  在一定的摄像机模型下，基于特定的实验条件，如已知参照物的形状、尺寸，进行图像处理，数学变换、技术方法，求取内外参数。
  此方法需要经常调整摄像机的需求、设置已知参照物，不现实。
  此类方法包括利用最优化算法的标定方法、利用摄像机变换矩阵的标定方法、进一步考虑畸变补偿的两步法、张正友标定法。
• 自标定法
  不依赖参照物，利用摄像机本身参数之间的约束关系来标定，利用周围图像与图像之间的对应关系，与场景和摄像机运动无关。
  此类方法包括基于Krupa方程、分层逐步标定法、基于二次曲面自标定法。

三、张氏标定法

【张氏标定法】是张正友博士在1999年发表在国际顶级会议ICCV上的论文《Flexible Camera Calibration By Viewing a Plane From Unknown Orientations》中，提出的一种利用平面棋盘格进行相机标定的实用方法。该方法介于摄影标定法和自标定法之间，既克服了摄影标定法需要的高精度三维标定物的缺点，又解决了自标定法鲁棒性差的难题。**标定过程仅需使用一个打印出来的棋盘格，并从不同方向拍摄几组图像即可，任何人都可以制作标定图案，不仅使用灵活方便，而且精度很高，鲁棒性好。
**

1. 棋盘

棋盘是一块由黑白方块间隔组成的标定板，我们用它来作为相机标定的标定物（从真实世界映射到数字图像内的对象）。之所以我们用棋盘作为标定物是因为平面棋盘模式更容易处理（相对于复杂的三维物体），但与此同时，二维物体相对于三维物体会缺少一部分信息，于是我们会多次改变棋盘的方位来捕捉图像，以求获得更丰富得坐标信息。如下图所示，是相机在不同方向下拍摄的同一个棋盘图像。

基于世界坐标系与像素坐标系之间的关系转换，其中世界坐标系是我们自己设定的，故可以假设标定棋盘位于世界坐标系中$Z_w=0$的平面。由于$Z_w=0$，故公式可以变为：

2. 单应性（Homography）变换

单应性变换用于描述物体在世界坐标系和像素坐标系之间的位置映射关系，对应的变换矩阵称为单应性矩阵。在上面的公式中，单应性矩阵定义为（其中M是内参矩阵）：

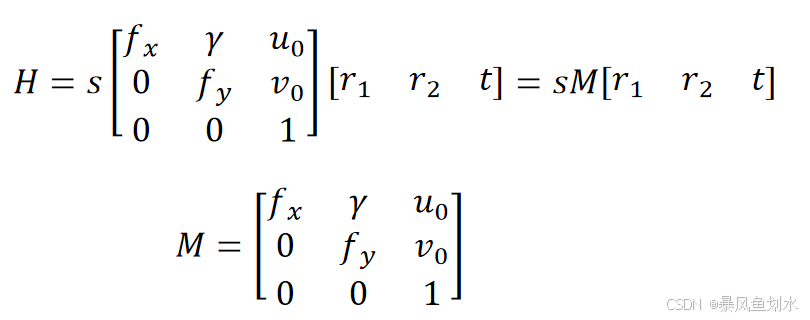
单应性在计算机视觉领域是一个非常重要的概念，它在图像校正、图像拼接、相机位姿估计、视觉SLAM等领域有非常重要的作用。

• 图像校正
  下图是单应性矩阵进行图像校正的示例，左边倾斜的楼栋至右边非倾斜楼栋至少需要四个对应点。
  
• 视角变换
  下图是单应性矩阵进行视角变换的示例，左边普通视图至鸟瞰图。
  
• 图像拼接
  既然单应性矩阵可以进行视角变换，那可以把不同角度拍摄的图像都转换到同样的视角下，就可以实现图像拼接了。如下图所示，通过单应性矩阵H可以将image1和image2都变换到同一个平面。
  
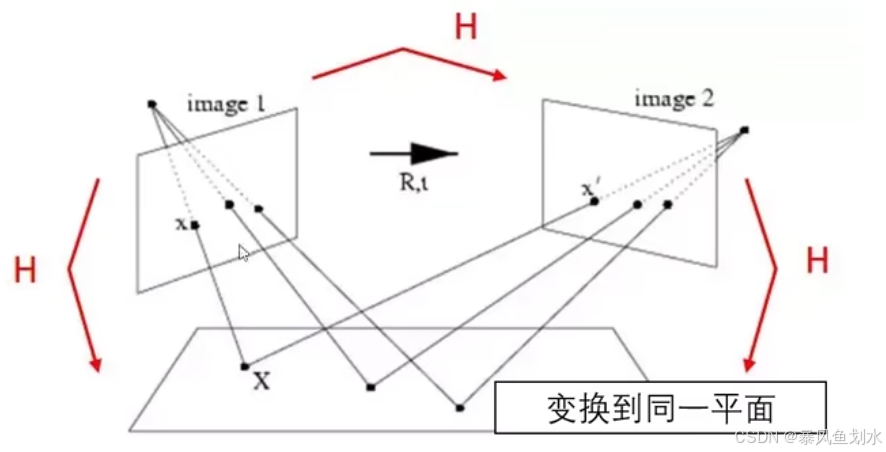
• 增强现实（AR）
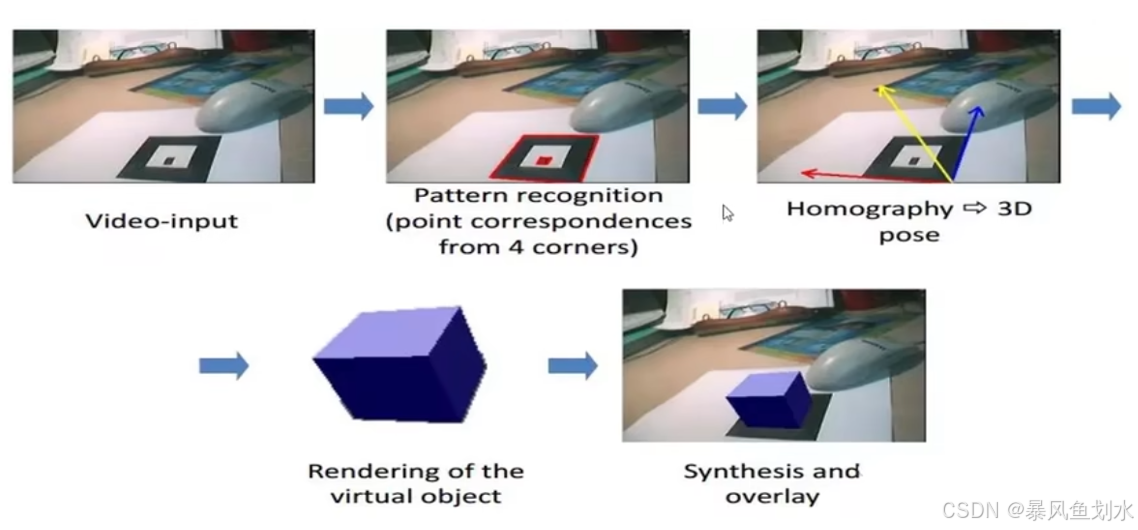
  平面二维标记图案（marker）经常用来做AR展示。根据marker不同视角下的图像可以方便的得到虚拟物体的位置姿态并进行显示，如下图所示。
  

3. 如何估计单应性矩阵？

首先，我们假设两张图像中的对应点对的齐次坐标为$(x^{\prime },y^{\prime },1)$和$(x,y,1)$，单应性矩阵$H$定义为：$H=\left[\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right]$
则有：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]\sim \left[\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$
矩阵展开后有3个等式，将第3个等式带入前两个等式中可得：
$$\{\begin{array}{r}{x}^{\prime }=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\ y^{\prime }=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}\end{array}$$
也就是说，一个点对对应两个等式。
此处引出一个问题：单应矩阵H有几个自由度？也就是说，有几个独立变量？
可能大家会说有9个，H矩阵不是有9个参数吗？从$h_{11}$到$h_{33}$总共9个。但实际上并不是，因为这里使用的是齐次坐标系，也就是说可以进行任意尺度的缩放。比如我们将$h_{ij}$乘以任意一个非零常数$k$并不改变等式结果：
$$\{\begin{array}{r}{x}^{\prime }=\frac{k{h}_{11}x+k{h}_{12}y+k{h}_{13}}{k{h}_{31}x+k{h}_{32}y+k{h}_{33}}\\ y^{\prime }=\frac{k{h}_{21}x+k{h}_{22}y+k{h}_{23}}{k{h}_{31}x+k{h}_{32}y+k{h}_{33}}\end{array}\to \{\begin{array}{r}{x}^{\prime }=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\ y^{\prime }=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}\end{array}$$
所以实际上单应矩阵H只有8个自由度。8自由度下计算单应矩阵H：
$$\begin{gathered} \{\begin{array}{r}{x}^{\prime }=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}\\ y^{\prime }=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}\end{array} \\ {h}_{11}^2+h_{12}^2+h_{13}^2+h_{21}^2+h_{22}^2+h_{23}^2+h_{31}^2+h_{32}^2+h_{33}^2=1 \end{gathered}$$
乘以分母展开：
$$\begin{gathered} (h_{31}x+h_{32}y+h_{33})x^{\prime }=h_{11}x+h_{12}y+h_{13} \\ (h_{31}x+h_{32}y+h_{33})y^{\prime }=h_{21}x+h_{22}y+h_{23} \end{gathered}$$
整理得到：
$$\begin{gathered} h_{11}x+h_{12}y+h_{13}-h_{31}x{x}^{\prime }-h_{32}y{x}^{\prime }-h_{33}{x}^{\prime }=0 \\ {h}_{21}x+h_{22}y+h_{23}-h_{31}x{y}^{\prime }-h_{32}y{y}^{\prime }-h_{33}{y}^{\prime }=0 \end{gathered}$$
假设我们得到了两幅图像中对应的N个点对（特征点匹配对），那么可以得到如下线性方程组：

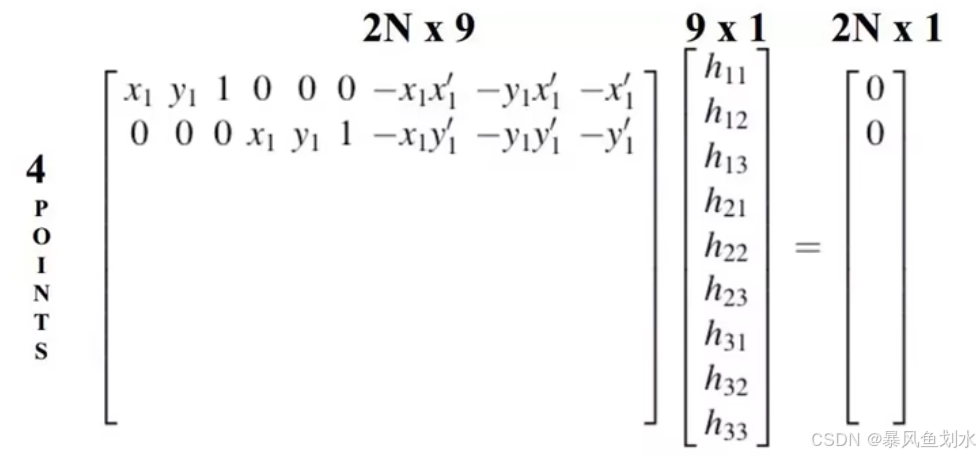
根据该线性方程组可以看出，一个点对可以确定两个方程，我们共有9个参数及一个约束条件，故代求参数共8个，因此，至少需要四个点对确定八个方程。
也就是说单张标定图像，必须要4个特征点被提取出来，我们的棋盘格远多于这个值，因此会有较好的效果。
但是以上只是理论推导，在真实的应用场景中，我们计算的点对中都会包含噪声。比如点的位置偏差几个像素，甚至出现特征点对误匹配的现象，如果只使用4个点对来计算单应矩阵，那会出现很大的误差。因此，为了使得计算更精确，一般都会使用远大于4个点对来计算单应矩阵。另外，上述方程组采用直接线性解法通常很难得到最优解，所以实际使用中一般会用其他优化方法。如奇异值分解、Levenberg-Marquarat(LM)算法等进行求解。

本节内容暂时到这里，下节将讲解张氏相机标定法推导求解。