算法题（246）：负环（bellman_ford算法）

审题：

本题需要我们判断图中是否存在负环

思路：

方法一：bellman_ford算法

在bellman_ford算法中，我们已经知道正常情况下最多只会进行n-1轮松弛操作，如果存在负环会就一直进行松弛操作，所以我们可以把松弛操作轮数限定为n轮，如果第n轮中仍然进行了松弛操作，那么就说明有负环，否则就没有

解题：
 

#include<iostream>
using namespace std;
const int N = 2e3 + 10, M = 3e3 + 10;
int t, n, m;
int pos;
int dist[N];
struct node
{int l, r, v;
}e[2*M];
bool bf()
{//初始化dist数组for (int i = 1; i <= n; i++){dist[i] = 0x3f3f3f3f;}dist[1] = 0;bool flags = false;for (int i = 1; i <= n; i++){flags = false;for (int j = 1; j <= pos; j++){int l = e[j].l, r = e[j].r, v = e[j].v;if (dist[l] == 0x3f3f3f3f) continue;//if (dist[r] > dist[l] + v){dist[r] = dist[l] + v;flags = true;}}if (flags == false) return false;//没有进行松弛操作，没有负环直接返回}return true;
}
int main()
{cin >> t;while (t--){pos = 0;cin >> n >> m;for (int i = 1; i <= m; i++){int x, y, z; cin >> x >> y >> z;pos++;e[pos].l = x; e[pos].r = y; e[pos].v = z;if (z >= 0)//双向边{pos++;e[pos].l = y; e[pos].r = x; e[pos].v = z;}}if (bf()) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}

关键1：当权值大于等于0的时候是双向边关系，需要记录好

关键2：负环判断具体实现

进行n轮松弛操作，如果提前检测到flags为false，说明没有负环

如果进行了n轮都没有检测到flags为false，说明第n轮仍然有松弛操作，一定有负环存在

关键3：松弛操作之前要进行节点可达性检查

如果不检查将要进行松弛操作的节点是否dist为无穷大，可能会出现多轮无效松弛

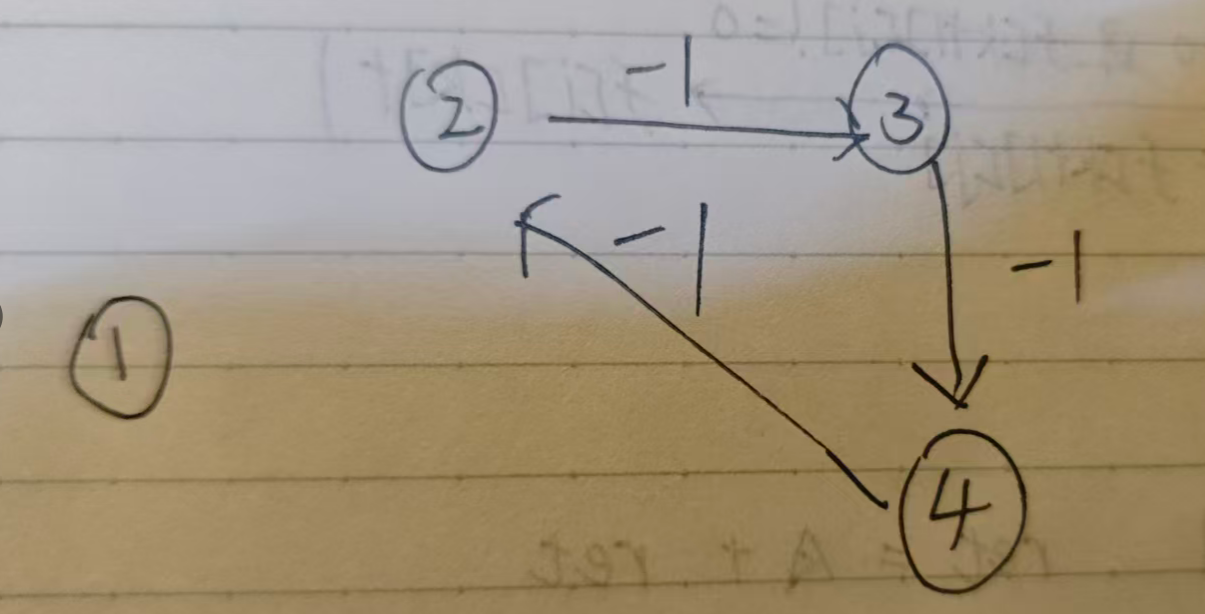
比如：

1

4 3

2 3 -1

3 4 -1

4 2 -1

图关系如下：

这里虽然有负环，但是无法从起点1到达，所以正确答案应该是NO，可是不进行节点可达性检测，就会让右侧三个节点不断进行松弛操作，从而让返回值变为trueP3385 【模板】负环 - 洛谷