4.前缀和

一.一维前缀和

题目连接如下:

https://ac.nowcoder.com/acm/problem/226282

1.算法分析

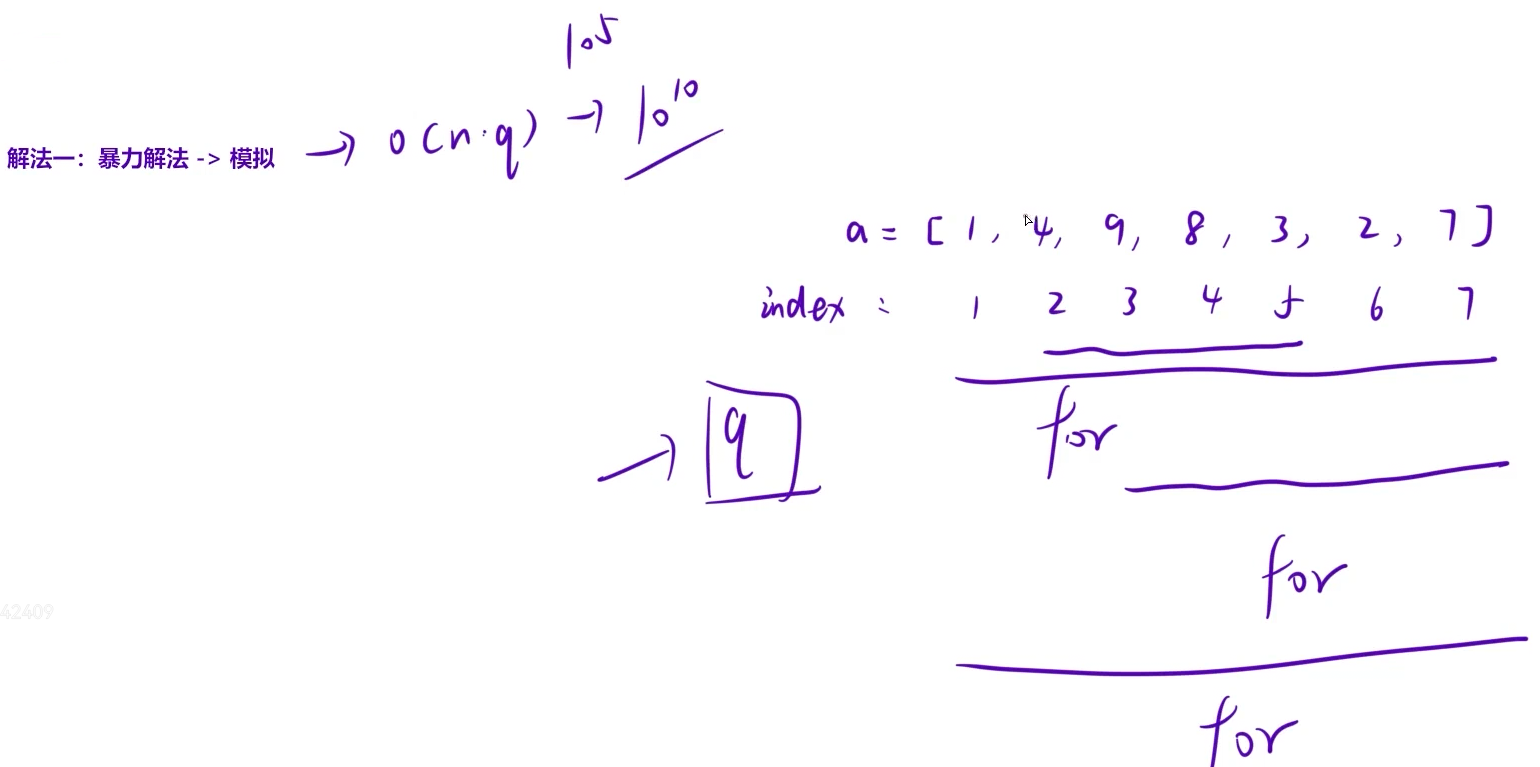
暴力解法会超时的,这里就不讲解了

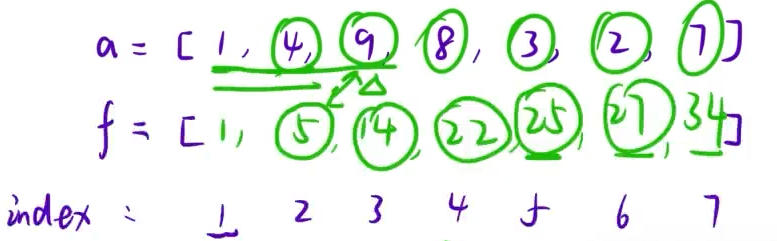
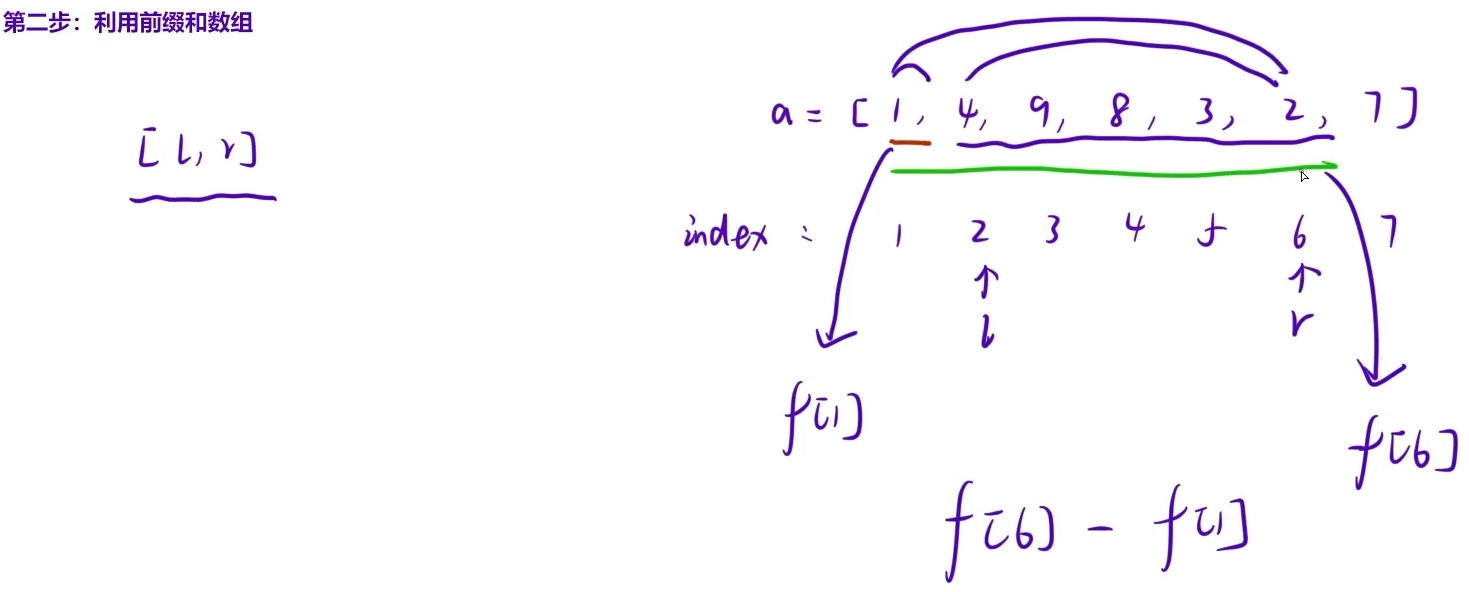
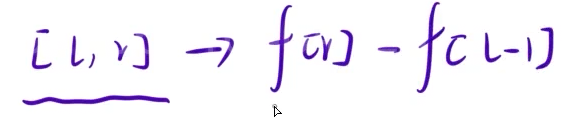
2.代码实现

#include <iostream>using namespace std;
typedef long long LL;const int N = 1e5 + 10;
int n,q;
LL a[N];
LL f[N]; //前缀和数组int main()
{cin >> n >> q;for(int i = 1;i <= n; i++){cin >> a[i];}//处理前缀和数组for(int i = 1;i <= n;i++){f[i] = f[i - 1] + a[i];}while(q--){int l,r;cin >> l >> r;cout << f[r] - f[l - 1] << endl;}return 0;
}

二.最大字段和

题目连接如下:

https://www.luogu.com.cn/problem/P1115

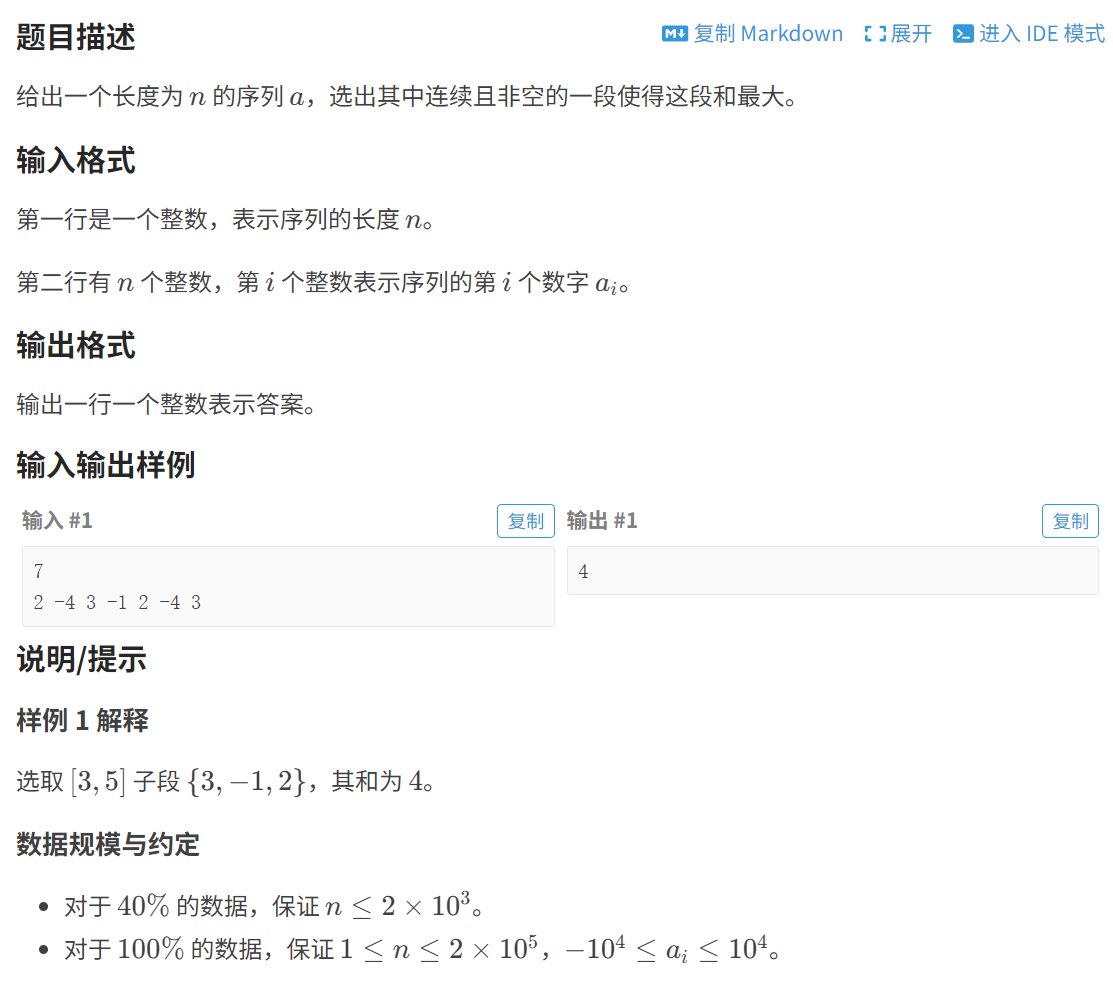
1.算法分析

2.代码实现

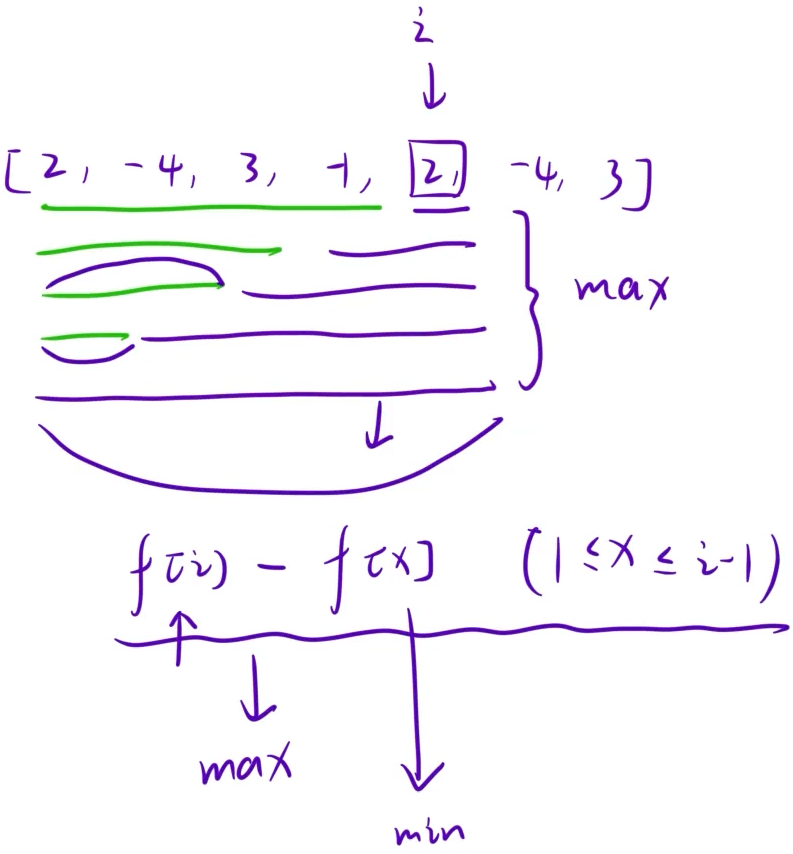
每一次我们的prevmin都是通过我们的f[i]来进行更新的

#include <iostream>using namespace std;
typedef long long LL;const int N = 2e5 + 10;int n;
LL f[N]; // 前缀和数组int main()
{cin >> n;for(int i = 1;i <= n;i++){LL x;cin >> x;f[i] = f[i - 1] + x;}LL ret = -1e20;LL prevmin = 0;for(int i = 1;i <= n;i++){ret = max(ret,f[i] - prevmin);prevmin = min(prevmin,f[i]);}cout << ret << endl;return 0;
}

三.二维前缀和

题目连接如下:

https://ac.nowcoder.com/acm/problem/226333

1.算法分析

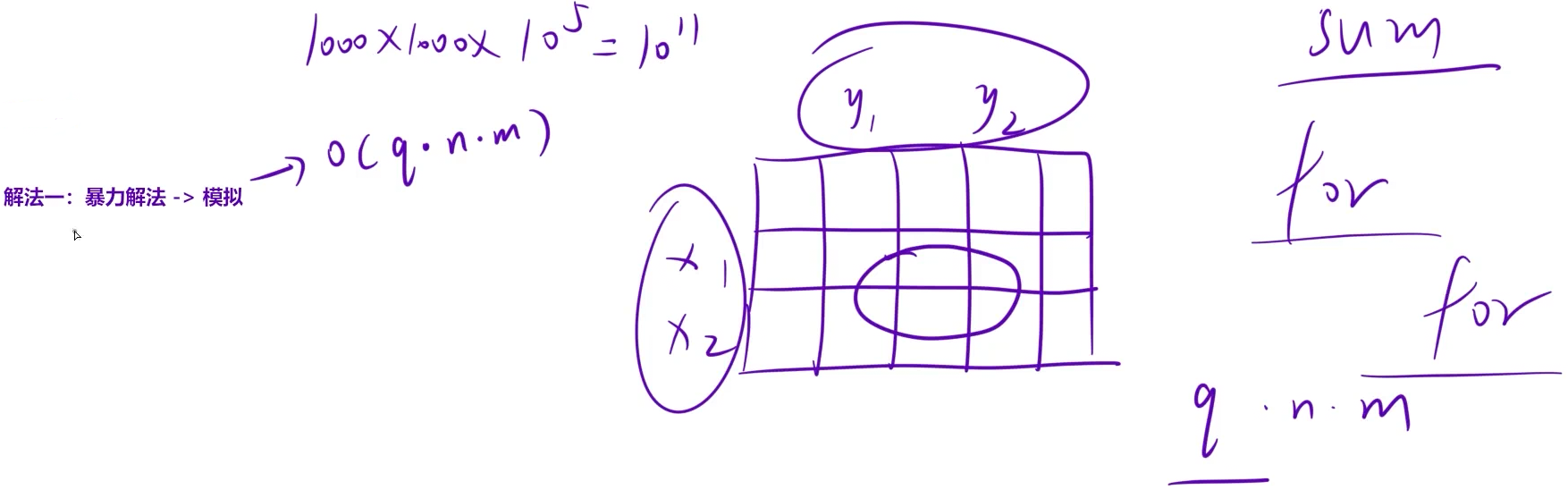
上面暴力还是会超时的

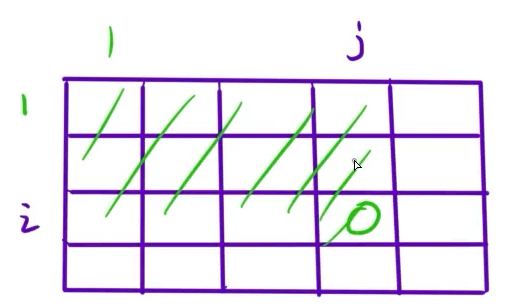
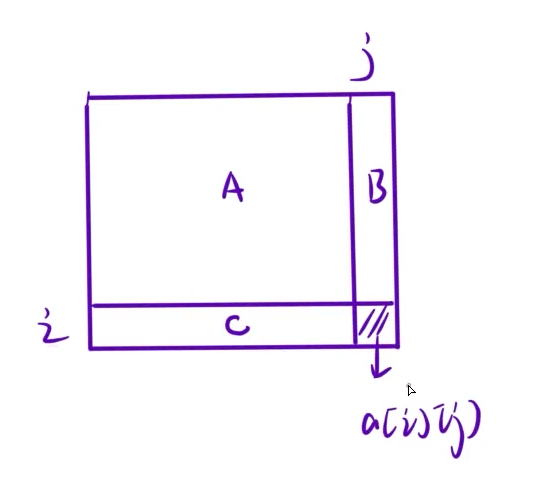
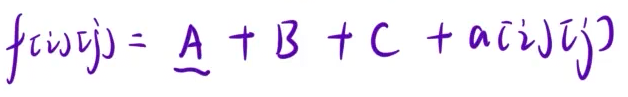
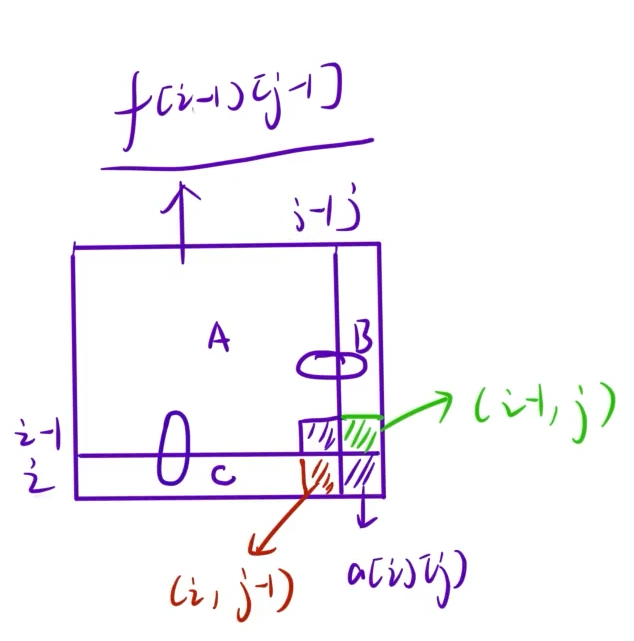
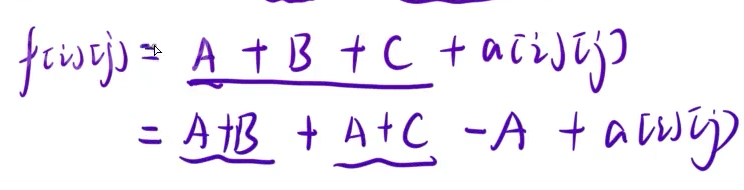
最终得出我们的结论,如下:

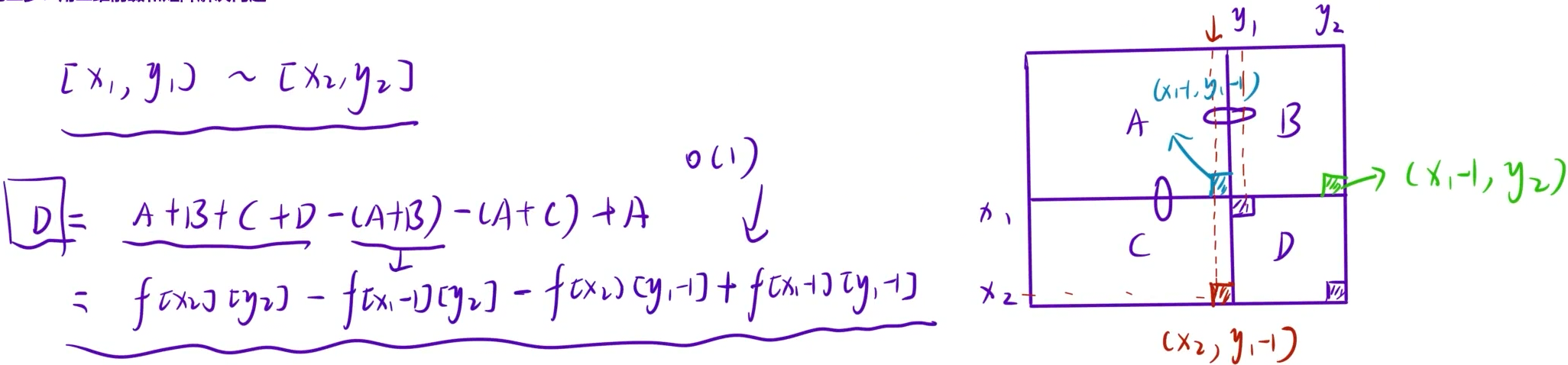
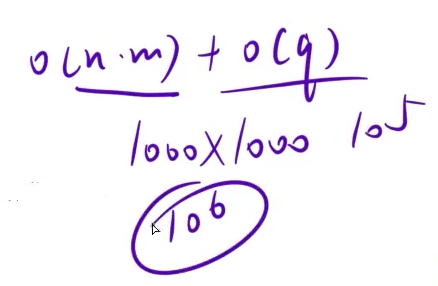
2.代码实现

#include <iostream>using namespace std;
typedef long long LL;const int N = 1010;
int n,m,q;
LL f[N][N];int main()
{cin >> n >> m >> q;for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){LL x;cin >> x;f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;}}while(q--){int x1,y1,x2,y2;cin >> x1 >> y1 >> x2 >> y2;cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;}return 0;
}

四.激光炸弹

题目连接如下:

https://www.luogu.com.cn/problem/P2280

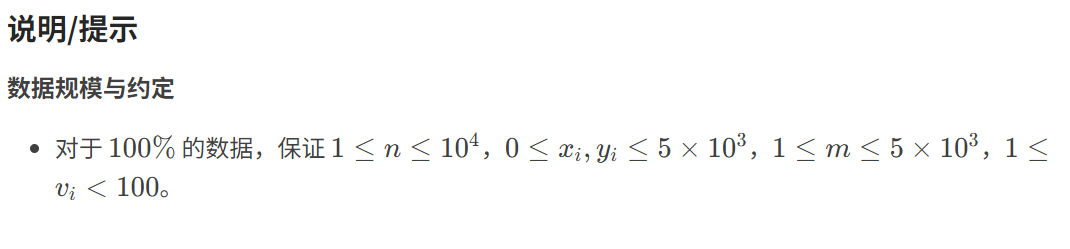
1.算法分析

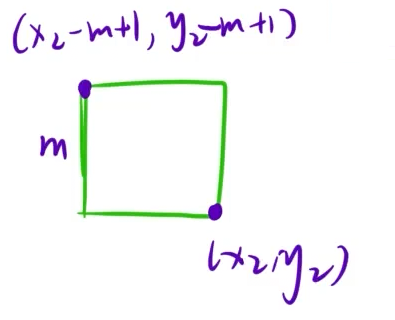
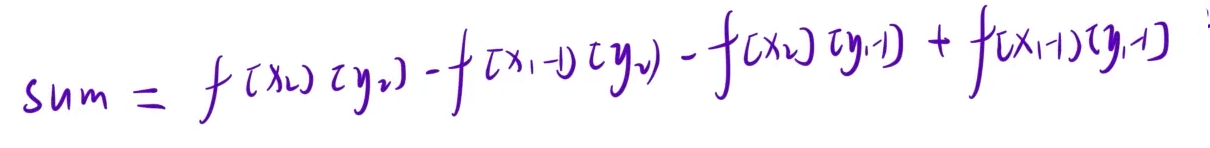
2.代码实现

#include <iostream>using namespace std;
typedef long long LL;const int N = 5010;
int n,m;
int a[N][N];
int f[N][N]; //前缀和矩阵int main()
{cin >> n >> m;while(n--){int x,y,v;cin >> x >> y >> v;x++,y++;a[x][y] += v;}n = 5001;for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){f[i][j] = f[i-1][j] + f[i][j - 1]-f[i-1][j-1]+a[i][j];}}int ret = 0;m = min(m,n);//如果炸弹很大,就拿全部的for(int x2 = m;x2 <= n;x2++){for(int y2 = m;y2 <= n;y2++){int x1 = x2 - m + 1,y1 = y2 - m + 1;ret = max(ret,f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);}}cout << ret << endl;return 0;
}