计算机图形学：【Games101】学习笔记02——变换（二维与三维、模型、视图、投影）

前言

• 🎮 GAMES101 是国内相当有名的图形学公开课。项目相关资源在：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html。
• 本 📒笔记为 🖊️笔者在自学过程中整理的 🇨🇳中文版笔记，供各位 📖读者阅读 😼～
• 图形变换是计算机图形学的 “核心操作”—— 无论是游戏中角色的移动、电影中镜头的切换，还是 3D 模型到 2D 屏幕的投影，本质都是通过变换实现的。本章聚焦 2D 基本变换、齐次坐标（解决平移的矩阵表示问题）、变换组合，以及 3D 变换的基础，内容紧密衔接上一讲的线性代数知识，下面逐模块梳理。

一、变换（二维与三维）

1.1 为什么要学图形变换？（Why Transformation？）

  没有变换，就无法 “操作” 和 “观察” 虚拟物体：

• 建模（Modeling）：构建与调整虚拟物体建模是创建 3D 场景的过程，变换用于调整物体的位置、姿态和大小：
  • 平移（Translation）：将物体从一个位置移动到另一个位置（如游戏中角色向前走）；
  • 旋转（Rotation）：改变物体的朝向（如角色转身、车轮转动）；
  • 缩放（Scaling）：放大或缩小物体（如近大远小的视觉效果，或调整模型尺寸以匹配场景）。
• 视图（Viewing）：从 3D 到 2D 的投影
  • 我们最终看到的屏幕画面是 2D 的，视图变换用于将 3D 场景 “投影” 到 2D 屏幕上：
  • 核心逻辑：模拟人眼或相机的 “观察过程”—— 从 3D 世界中的观察点出发，将物体投射到 2D 成像平面，形成最终的图像；
  • 本质：是一种特殊的 3D 到 2D 的变换。

1.2 2D基本变换：旋转、缩放、剪切（线性变换）

  2D 变换是图形变换的基础，首先介绍 “线性变换”—— 可通过2×2 矩阵表示的变换（满足 “可加性” 和 “齐次性”），包括缩放、剪切、旋转。

1.2.1 缩放变换（Scale）

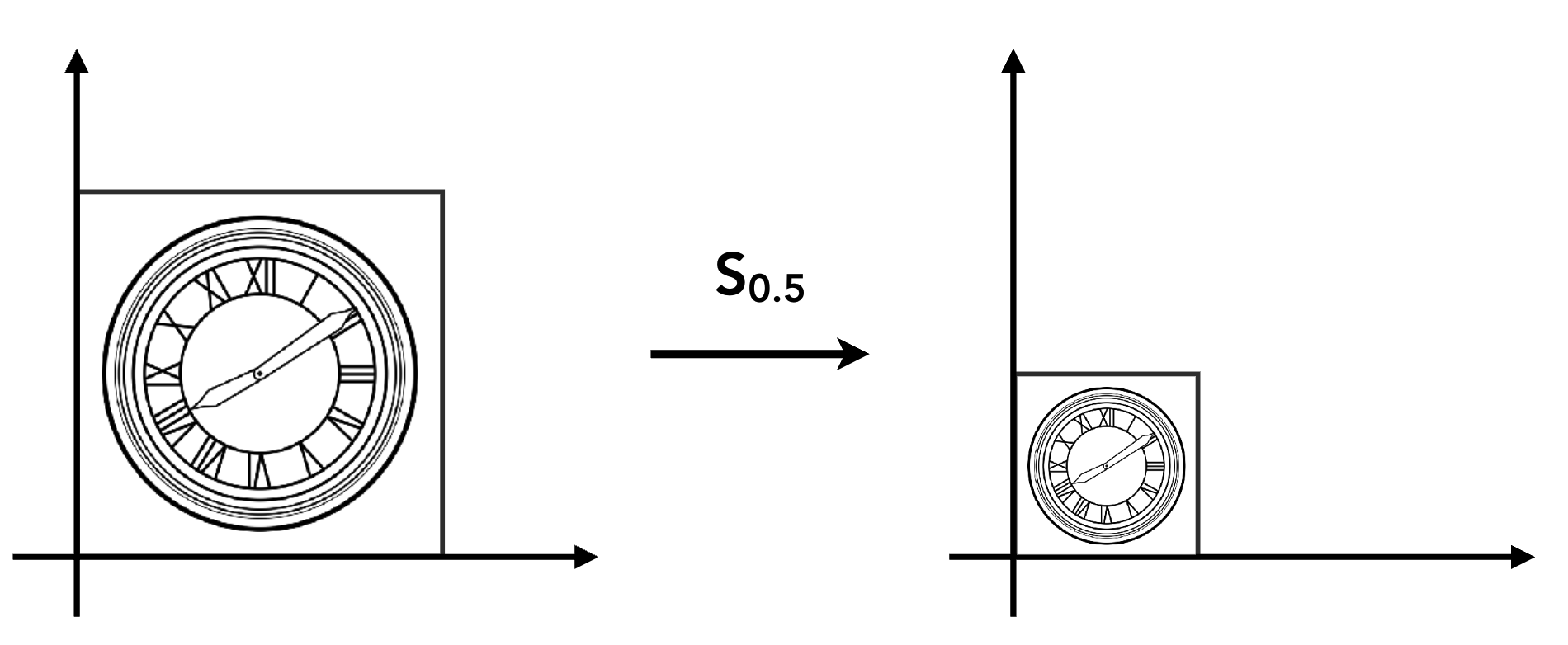
  缩放变换通过改变物体在 x 轴和 y 轴方向的尺寸实现，分为 “均匀缩放” 和 “非均匀缩放”。

• 均匀缩放：x 轴和 y 轴缩放系数相同（如整体放大 2 倍、缩小为 0.5 倍）；
  • 公式（2D 点 $(x,y)$ 经缩放后变为 $(x^{\prime },y^{\prime })$ ）：$x^{\prime }=s\cdot x$，$y^{\prime }=s\cdot y$（s为缩放系数）；
  • 矩阵表示：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$；
    
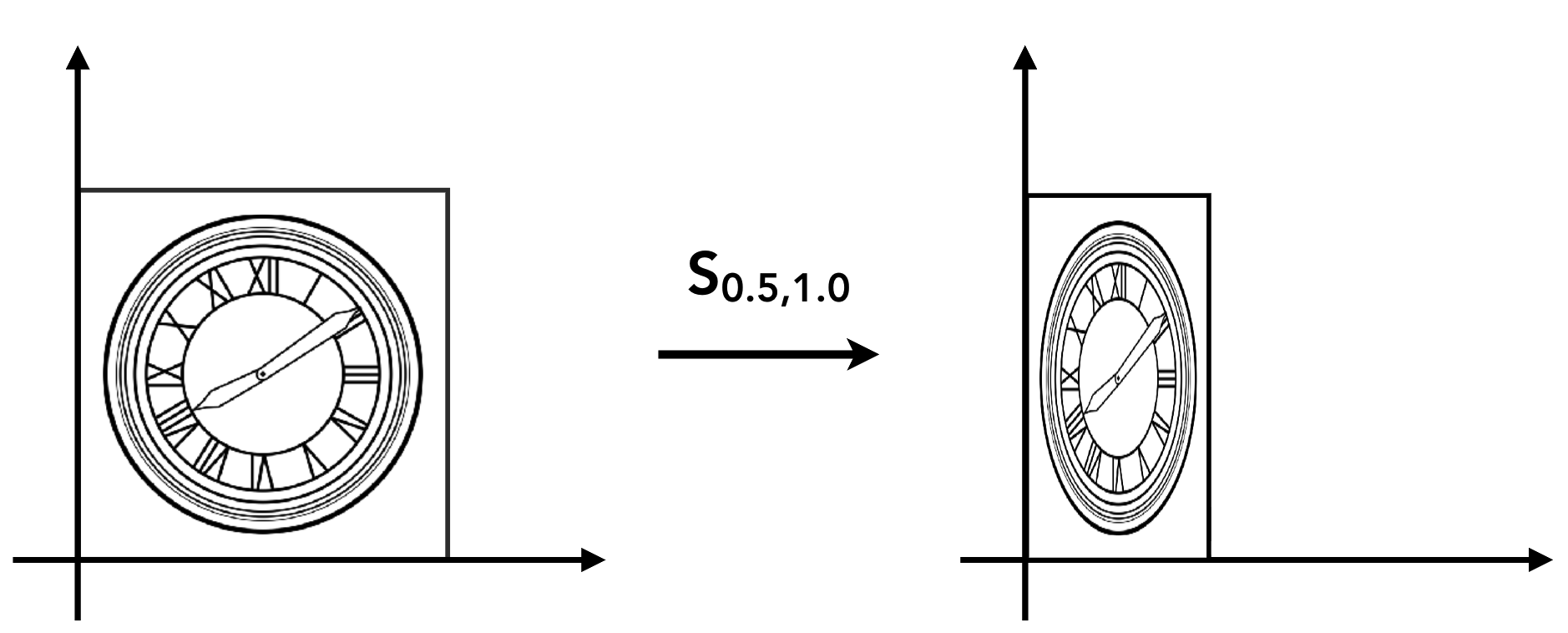
• 非均匀缩放：x 轴和 y 轴缩放系数不同（如 x 轴缩为 0.5 倍，y 轴保持不变）；
  • 公式：$x^{\prime }=s_x\cdot x$，$y^{\prime }=s_y\cdot y$（$s_x$ 为 x 轴系数，$s_y$ 为 y 轴系数）；
  • 矩阵表示：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$；
    
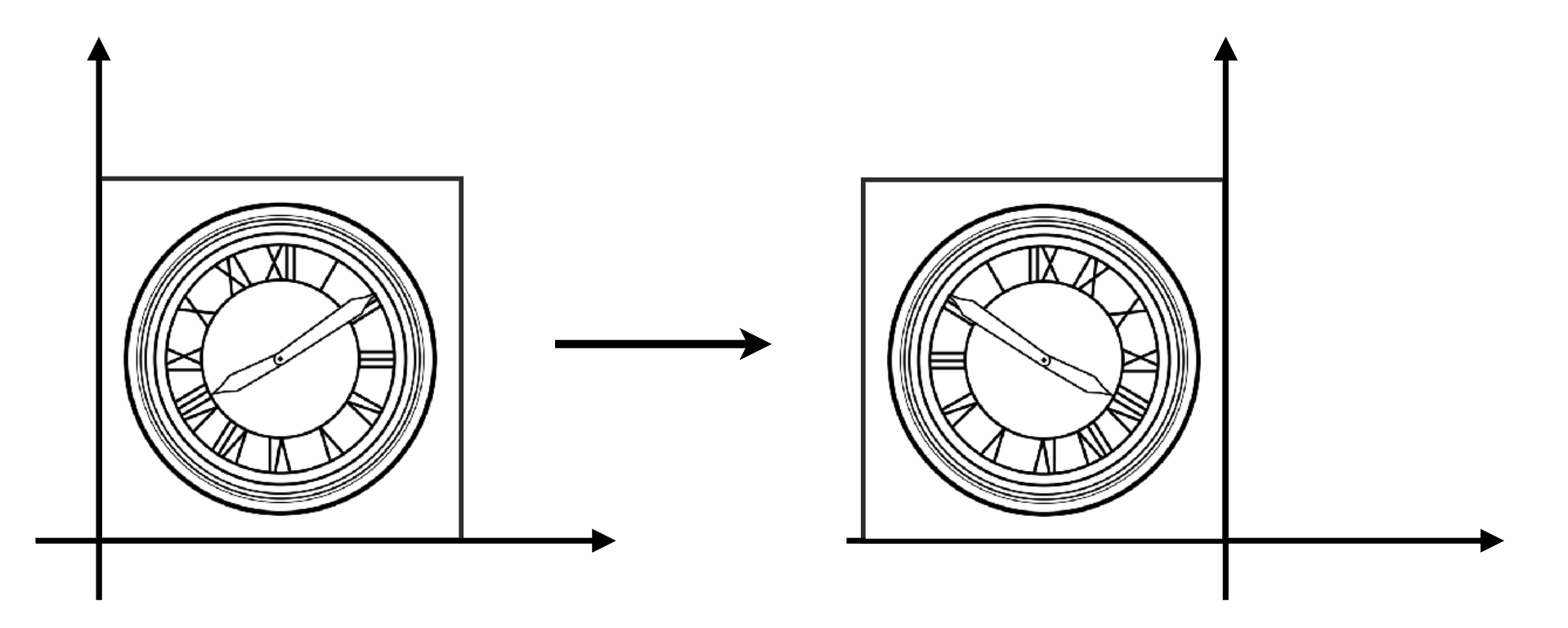
• 特殊情况：反射（Reflection）：可视为 “负缩放”，如 x 轴反射（$s_x=-1，s_y=1$），矩阵为 $\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$，效果是物体关于 y 轴对称。
  

1.2.2 剪切变换（Shear）

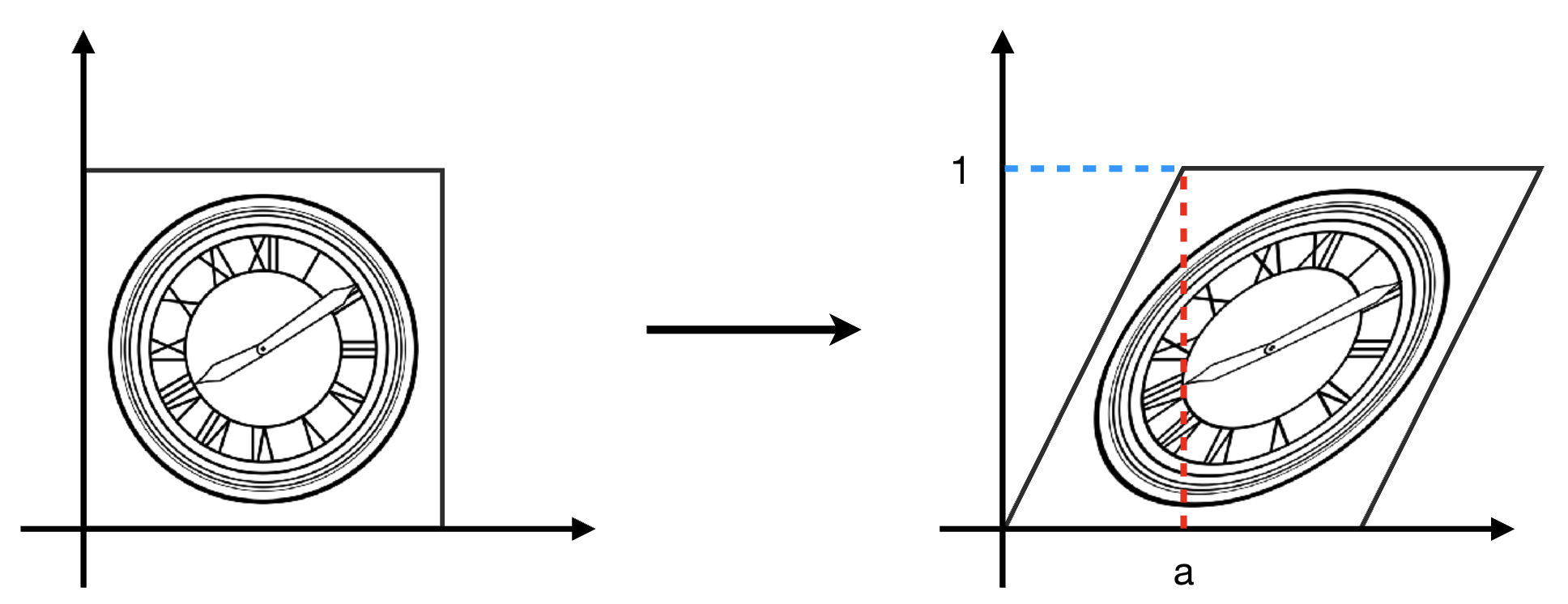
  剪切变换使物体沿某一轴方向发生倾斜，常用的是 “水平剪切”（x 轴随 y 轴变化）。

• 水平剪切逻辑：y=0 处的点不移动，y=1 处的点沿 x 轴平移a个单位，中间点按比例平移；
• 公式：$x^{\prime }=x+a\cdot y$，$y^{\prime }=y$（a为剪切系数）；
• 矩阵表示：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$；
• 示例：若 a=1，则点 (0,1) 变为 (1,1)，点 (1,1) 变为 (2,1)，正方形会变成平行四边形。
  

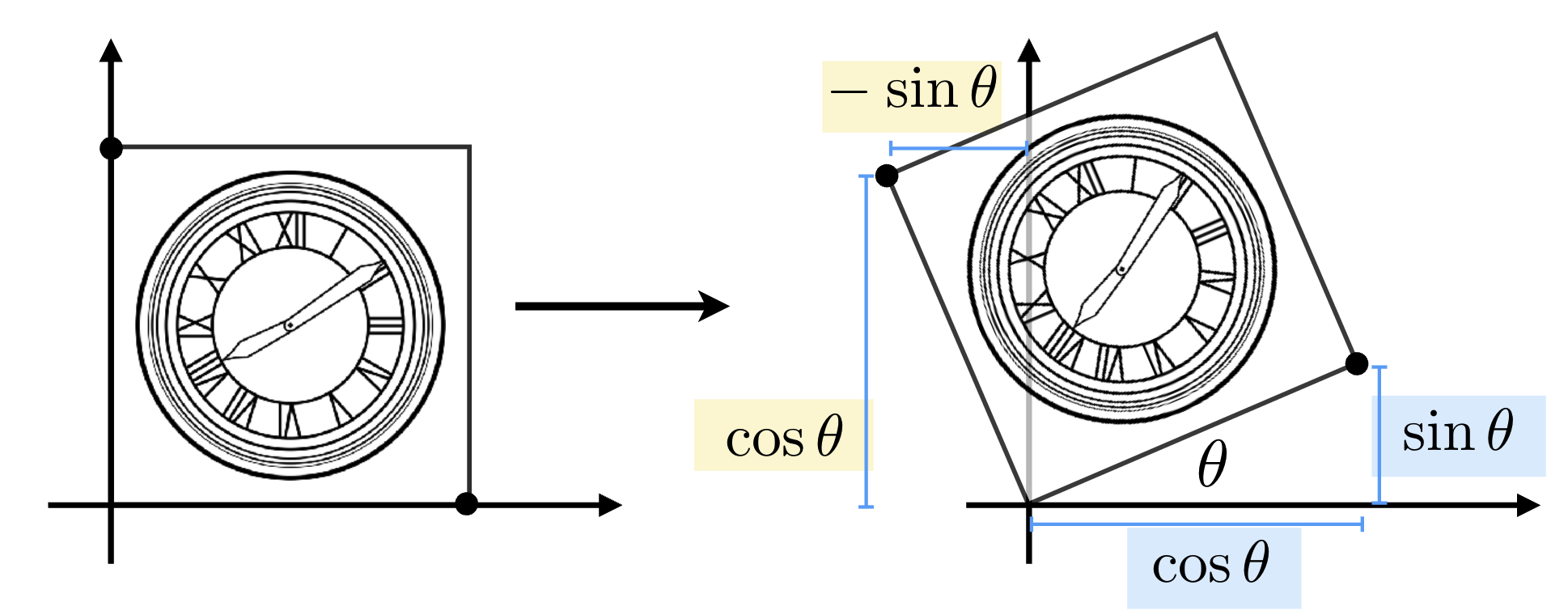
1.2.3 旋转变换（Rotation）

  默认情况下，旋转变换是 “绕坐标原点（0,0）逆时针旋转 $\alpha$ 角”，是图形学中最常用的变换之一。

• 公式推导：基于三角函数的投影 —— 设原向量长度为r，与 x 轴夹角为 $\theta$，旋转后夹角变为 $\theta +\alpha$，则：

  • $x^{\prime }=r\cdot \cos (\theta +\alpha )=r\cos \theta \cos \alpha -r\sin \theta \sin \alpha =x\cos \alpha -y\sin \alpha$；
  • $y^{\prime }=r\cdot \sin (\theta +\alpha )=r\sin \theta \cos \alpha +r\cos \theta \sin \alpha =x\sin \alpha +y\cos \alpha$；

• 矩阵表示：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$；

• 注意：若要顺时针旋转，只需将 $\alpha$ 替换为 $-\alpha$（利用 $\cos (-\alpha )=\cos \alpha$， $\sin (-\alpha )=-\sin \alpha$，矩阵变为 $\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]$）。

1.2.4 线性变换的共性（Linear Transforms = Matrices）

  上述缩放、剪切、旋转均为线性变换，满足两个核心性质：

• 可加性：$T(\vec{a}+\vec{b})=T(\vec{a})+T(\vec{b})$；
• 齐次性：$T(k\vec{a})=kT(\vec{a}$（k为标量）；
• 矩阵表示：所有 2D 线性变换都可通过 2×2 矩阵表示，形式为 $\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$，变换结果为 $\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$。

1.3 齐次坐标：解决平移的 “特殊问题”

  线性变换能表示旋转、缩放、剪切，但无法表示平移—— 这是图形学中的一个关键 “痛点”，而齐次坐标是解决该问题的 “统一方案”。

• 平移的问题：不是线性变换
• 平移的公式是 $x^{\prime }=x+t_x$，$y^{\prime }=y+t_y$（$t_x,t_y$ 为 x、y 轴方向的平移量），显然不满足线性变换的性质（如 $T(\vec{a}+\vec{b})=T(\vec{a})+T(\vec{b})$ 不成立），因此无法用 2×2 矩阵表示：
• 若强行用矩阵表示，只能写成 “矩阵乘法 + 向量加法” 的形式：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$；
• 问题：平移成了 “特殊情况”，无法与其他线性变换统一用矩阵乘法表示，不利于后续组合变换。

1.3.1 2D 齐次坐标的定义（Homogeneous Coordinates）

  齐次坐标：增加一个额外的坐标（w 坐标），将 2D 点 / 向量表示为 3 维形式，从而用(3×3)矩阵统一表示所有变换（包括平移）。

• 2D 点：表示为 $(x,y,1{)}^T$（w=1）；
• 2D 向量：表示为 $(x,y,0{)}^T$（w=0）；
• 意义：通过 w 坐标区分 “点” 和 “向量”，且满足以下运算规则（符合直觉）：
  • 向量 + 向量 = 向量：$(x1,y1,0{)}^T+(x2,y2,0{)}^T=(x1+x2,y1+y2,0{)}^T$；
  • 点 - 点 = 向量：$(x1,y1,1{)}^T-(x2,y2,1{)}^T=(x1-x2,y1-y2,0{)}^T$；
  • 点 + 向量 = 点： $(x1,y1,1{)}^T+(x2,y2,0{)}^T=(x1+x2,y1+y2,1{)}^T$。

1.3.2 用齐次坐标表示平移

• 引入齐次坐标后，平移可通过 3×3 矩阵表示：平移公式的矩阵形式：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$；
• 验证：展开后为 $x^{\prime }=1\cdot x+0\cdot y+t_x=x+t_x，y^{\prime }=0\cdot x+1\cdot y+t_y=y+t_y$，完全符合平移公式。

1.3.3 统一所有 2D 变换

  此时，缩放、旋转、剪切也可升级为 3×3 矩阵，与平移统一：

• 缩放（Scale）：$S(s_x,s_y)=\left[\begin{array}{ccc}1& a& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$
• 旋转（Rotation）：$R(\alpha )=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]$
• 平移（Translation）：$T(t_x,t_y)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$

  这种 “线性变换 + 平移” 的组合，称为仿射变换（Affine Transformation） —— 齐次坐标的核心价值就是将仿射变换统一为单一矩阵乘法。

1.4 变换组合：多个变换的叠加

  实际场景中，物体的运动往往是 “多个变换的叠加”（如 “先平移再旋转”“先缩放再平移”），变换组合的核心是矩阵乘法，但需特别注意 “变换顺序”—— 矩阵乘法不满足交换律，顺序不同结果完全不同。

1.4.1 变换顺序的影响：先平移再旋转 vs 先旋转再平移

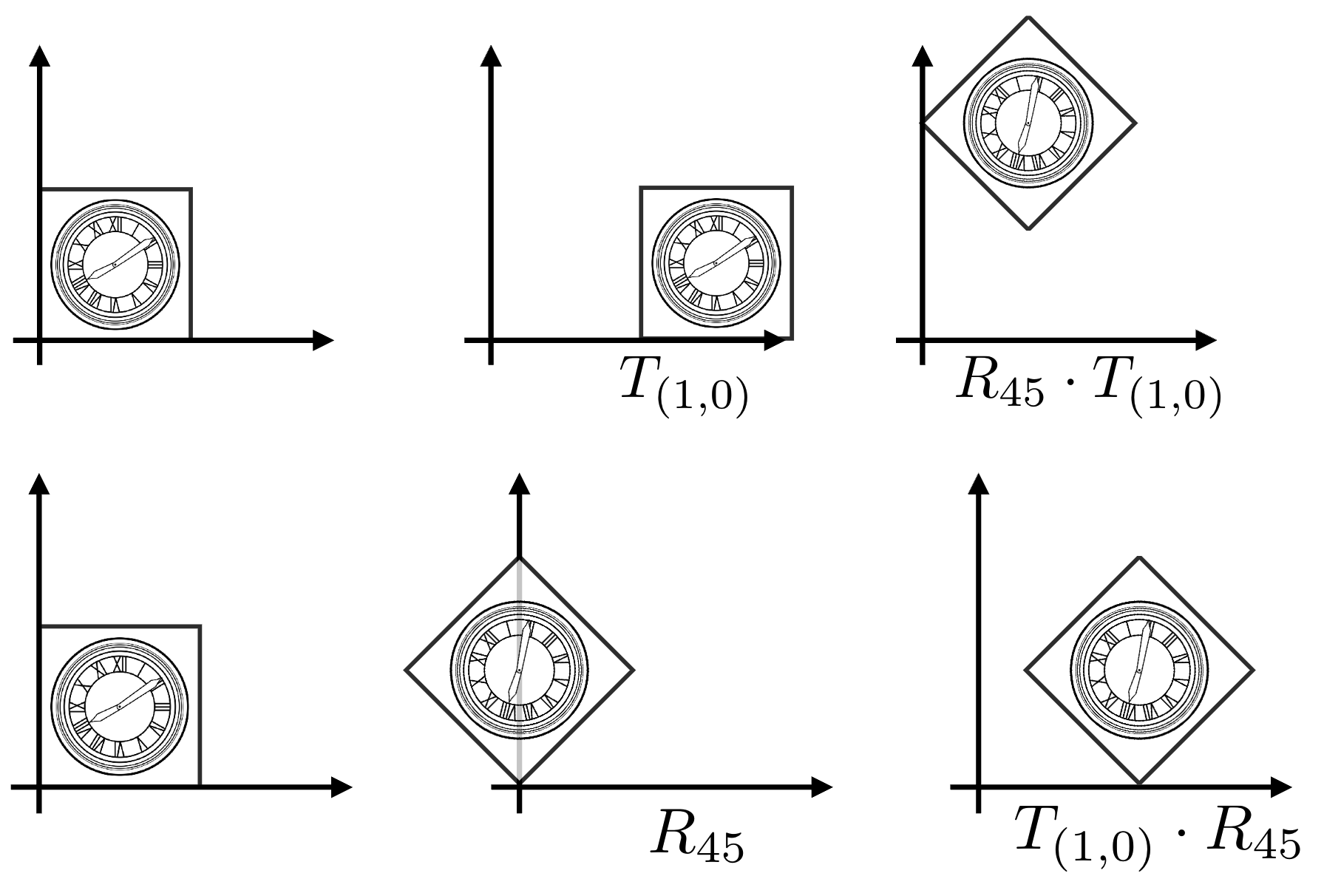
• 以 “点 (0,0) 先沿 x 轴平移 1 单位（ T(1,0) ），再逆时针旋转 45°（ R(45°) ）” 与 “先旋转再平移” 为例：
  • 先平移再旋转：变换矩阵为 $R(45°)\cdot T(1,0)$（矩阵乘法从右到左执行，即先算右侧的平移，再算左侧的旋转）；计算：T(1,0) 将 (0,0) 变为 (1,0)，再经 R(45°) 旋转，结果为 $\cos 45°,\sin 45°)\approx (0.707,0.707)$；
  • 先旋转再平移：变换矩阵为 $T(1,0)\cdot R(45°)$（先旋转，再平移）；计算：R(45°) 将 (0,0) 变为 (0,0) ，再经 T(1,0) 平移，结果为 (1,0)；
• 结论：$R(45°)\cdot T(1,0)\ne T(1,0)\cdot R(45°)$，变换顺序必须严格遵循 “右到左” 的执行逻辑（矩阵在左，变换在后；矩阵在右，变换在前）。
  

1.4.2 提升变换组合的效率：预乘矩阵

  若要对多个点执行相同的 “变换序列”（如场景中所有物体都执行 “缩放→旋转→平移”），直接逐个点执行多次变换会很耗时，高效做法是预乘所有变换矩阵：

• 逻辑：设变换序列为 $A_1,A_2,...,A_n$（依次执行 $A_1$ 到 $A_n$），则组合变换矩阵为$M=A_n\cdot ...\cdot A_2\cdot A_1$；
• 优势：只需计算一次M，后续每个点只需与M做一次矩阵乘法，即可完成所有变换，大幅提升效率；
• 公式：$A_n(...A_2(A_1(\vec{p})))=M\cdot \vec{p}$（ $\vec{p}$ 为点的齐次坐标）。

1.4.3 复杂变换的分解

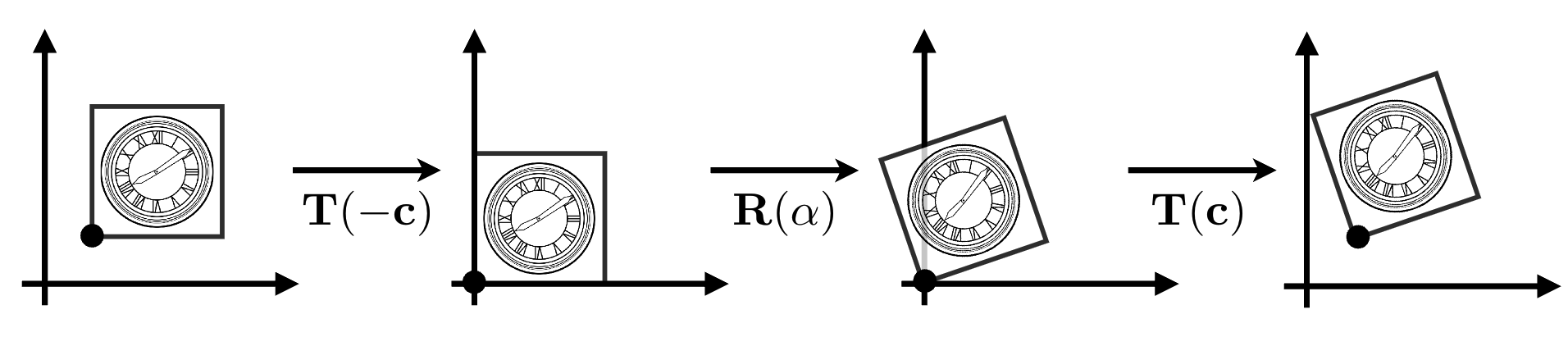
  以 “绕任意点 $c(c_x,c_y)$ 旋转 $\alpha$ 角” 为例，这类复杂变换可分解为 3 个基本变换的组合：

• 平移 1：将旋转中心c平移到原点（抵消c的位置），变换矩阵 $T(-c)=\left[\begin{array}{ccc}1& 0& -c_x\\ 0& 1& -c_y\\ 0& 0& 1\end{array}\right]$；
• 旋转：绕原点旋转 $\alpha$ 角，变换矩阵 $R(\alpha )$；
• 平移 2：将旋转中心从原点平移回c，变换矩阵 $T(c)=\left[\begin{array}{ccc}1& 0& c_x\\ 0& 1& c_y\\ 0& 0& 1\end{array}\right]$；
• 组合矩阵：$M=T(c)\cdot R(\alpha )\cdot T(-c)$（执行顺序：先 $T(-c)$，再 $R(\alpha )$，最后 $T(c)$ ）；
• 本质：将 “绕任意点的变换” 转化为 “绕原点的变换”+“平移补偿”，是图形学中处理复杂变换的通用思路。
  

1.5 3D 变换基础：扩展齐次坐标

  3D 变换是 2D 变换的自然扩展，核心思路仍是 “齐次坐标 + 矩阵乘法”，只是维度从 3 维升级到 4 维。

1.5.1 3D 齐次坐标的定义

• 3D 点：表示为 $(x,y,z,1{)}^T$（w=1）；
• 3D 向量：表示为 $(x,y,z,0{)}^T$（w=0）；
• 意义：与 2D 类似，通过 w 坐标区分点和向量，确保运算逻辑正确（如点 + 向量 = 点，点 - 点 = 向量）。

1.5.2 3D 仿射变换的矩阵表示

3D 仿射变换（线性变换 + 平移）通过 4×4 矩阵表示，形式如下：$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}a& b& c& t_x\\ d& e& f& t_y\\ g& h& i& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$；

• 左上 3×3 子矩阵：表示 3D 线性变换（如 3D 旋转、缩放、剪切）；
• 右侧 3×1 子矩阵：表示 3D 平移（ $t_x,t_y,t_z$ 分别为 x、y、z 轴的平移量）；
• 最下行：固定为 (0,0,0,1) ，确保齐次坐标的 w 分量保持为 1。

二、变换（模型、视图、投影）

2.1 3D变换进阶（3D Transformations）

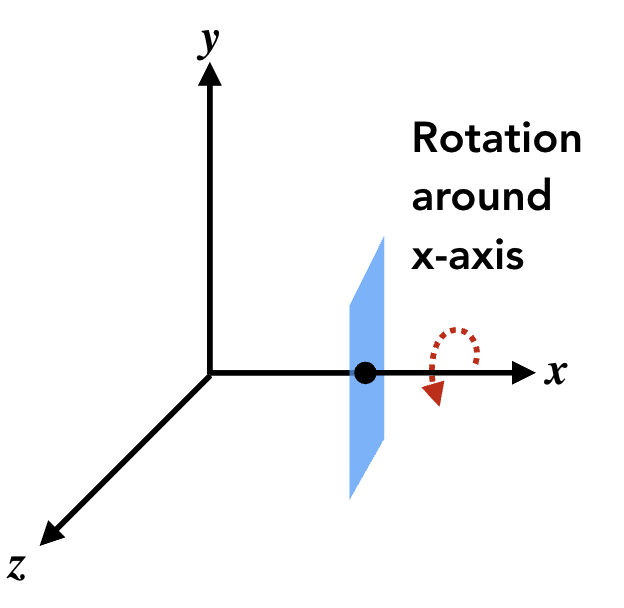
  3D 旋转比 2D 复杂，因为 3D 空间中有 3 个旋转轴（x、y、z 轴），且绕不同轴的旋转矩阵不同：

• 绕 x 轴旋转 $\alpha$ 角：$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \alpha & -\sin \alpha & 0\\ 0& \sin \alpha & \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right]$；
• 绕 y 轴旋转 $\alpha$ 角：$\left[\begin{array}{cccc}\cos \alpha & 0& \sin \alpha & 0\\ 0& 1& 0& 0\\ -\sin \alpha & 0& \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right]$；
• 绕 z 轴旋转 $\alpha$ 角：$\left[\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \sin \alpha & \cos \alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$；
  注意：3D 旋转的顺序同样重要，绕不同轴的旋转组合会产生复杂的姿态变化（如欧拉角的万向锁问题）。

2.2 3D 旋转进阶：从轴旋转到任意旋转

  上一讲仅介绍了绕 x/y/z 轴的 3D 旋转，而实际场景中物体的旋转往往是 “绕任意方向轴” 的（如游戏中角色的任意姿态调整），这部分将讲解两种核心解决方案：欧拉角与罗德里格斯公式。

2.2.1 欧拉角（Euler Angles）

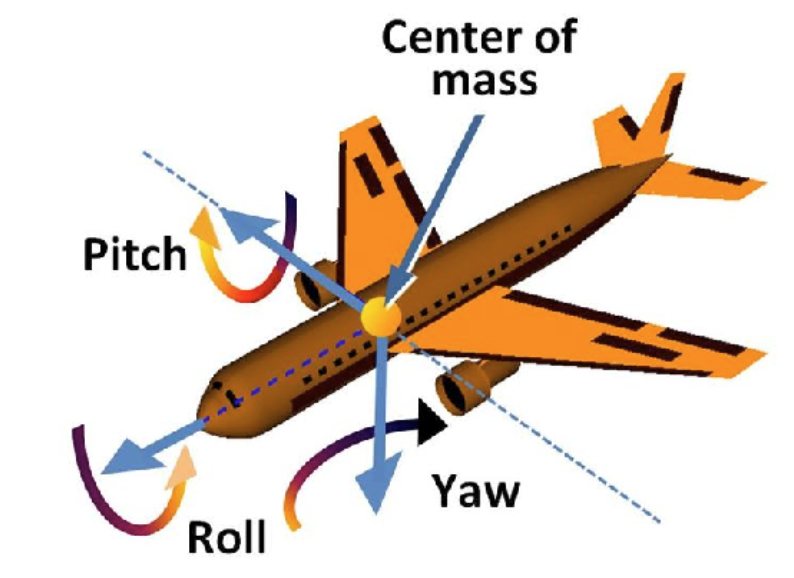
• 核心思想：将任意 3D 旋转分解为 “绕三个正交轴的连续旋转”，通过三个角度（如 roll、pitch、yaw）定义旋转姿态，常见于飞行模拟器、游戏角色控制等场景。
• 三个旋转分量定义（以 “物体自身坐标系” 为例）：
  • Roll（滚转）：绕物体自身 x 轴旋转（如飞机机翼上下倾斜）；
  • Pitch（俯仰）：绕物体自身 y 轴旋转（如飞机抬头或低头）；
  • Yaw（偏航）：绕物体自身 z 轴旋转（如飞机左右转向）；
• 矩阵表示：若旋转顺序为 “Roll→Pitch→Yaw”，则组合旋转矩阵为 $R=R_z(\gamma )\cdot R_y(\beta )\cdot R_x(\alpha )$（ $\alpha$ 为 roll 角，$\beta$ 为 pitch 角，$\gamma$ 为 yaw 角），遵循 “右到左” 的变换顺序。
• 欧拉角的问题：万向锁（Gimbal Lock）：这是欧拉角的致命缺陷 —— 当第二个旋转角（如 pitch）达到 ±90° 时，第一个和第三个旋转轴会重合，导致 “失去一个旋转自由度”，无法表示某些姿态。
  • 示例：当飞机抬头 90°（pitch=90°）时，roll（绕 x 轴）和 yaw（绕 z 轴）会都变成 “绕垂直于地面的轴旋转”，此时无法单独控制机翼倾斜；解决方案：引入 “四元数（Quaternion）。
    

2.2.2 罗德里格斯公式（Rodrigues’ Rotation Formula）

  当需要精确表示 “绕任意方向轴 $\vec{n}$ 旋转 $\alpha$ 角” 时，欧拉角无法直接使用，罗德里格斯公式提供了简洁的矩阵推导方法。

• 公式形式：设旋转轴为单位向量 $\vec{n}=(n_x,n_y,n_z{)}^T$，旋转角为 $\alpha$，则旋转矩阵 $R(\vec{n},\alpha )$ 为：$R(\vec{n},\alpha )=\cos \alpha \cdot I+(1-\cos \alpha )\cdot \vec{n}{\vec{n}}^T+\sin \alpha \cdot N$。其中：
  • I：3×3 单位矩阵；
  • $\vec{n}{\vec{n}}^T$：3×3 外积矩阵（由单位向量 $\vec{n}$ 构造，结果为对称矩阵），形式为：$\vec{n}{\vec{n}}^T=\left[\begin{array}{ccc}{n}_x^2& n_x{n}_y& n_x{n}_z\\ n_y{n}_x& n_y^2& n_y{n}_z\\ n_z{n}_x& n_z{n}_y& n_z^2\end{array}\right]$
  • $N：\vec{n}$ 的 “叉积对偶矩阵”，用于计算向量与 $\vec{n}$ 的叉积，形式为：$N=\left[\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right]$。
• 公式意义：罗德里格斯公式将 “绕任意轴的旋转” 分解为三个部分的叠加：
  • $\cos \alpha \cdot I$：保留原向量在垂直于旋转轴方向的分量；
  • $(1-\cos \alpha )\cdot \vec{n}{\vec{n}}^T$：将原向量投影到旋转轴上的分量保留；
  • $\sin \alpha \cdot N$：产生绕旋转轴的旋转分量；

2.3 视图变换（View / Camera Transformation）：把相机 “摆到正确位置”

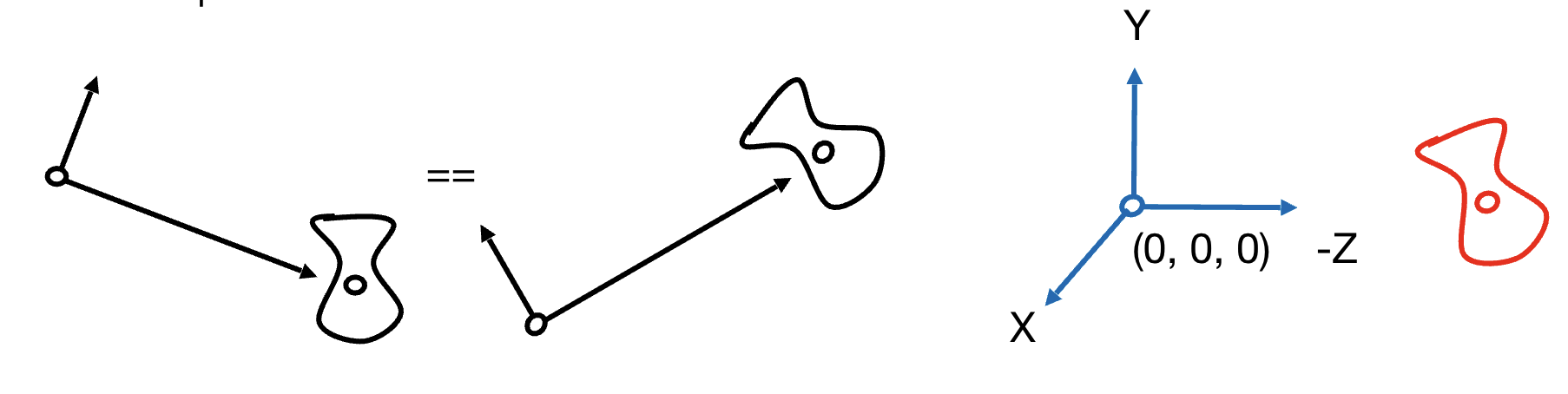
  视图变换是 “将 3D 场景转换为相机视角” 的第一步 —— 本质是通过变换让相机和场景一起移动，最终使相机处于 “标准位置”（原点、朝上为 Y 轴、看向 - Z 轴），方便后续投影计算。

  1️⃣ 视图变换的直观理解：模拟拍照过程

拍照分为三步，对应图形学中的三类变换：

• 建模变换（Model Transformation）：摆放场景中的物体（如调整人物姿势、位置）；
• 视图变换（View Transformation）：调整相机的位置和角度（找一个好的拍摄角度）；
• 投影变换（Projection Transformation）：按下快门，将 3D 场景投影为 2D 图像。

  2️⃣ 相机的三个关键参数（定义相机状态）

要执行视图变换，首先需要明确定义相机的初始状态，用三个参数描述：

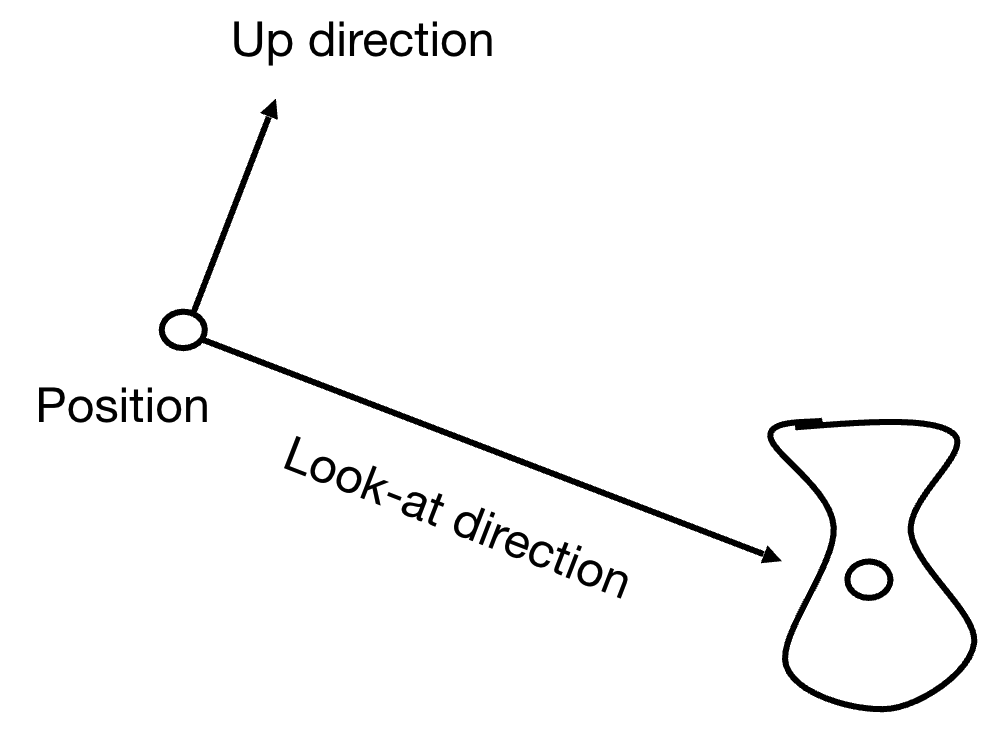
• 相机位置（Position）：记为 $\vec{e}$（相机光心的 3D 坐标）；
• 观察方向（Look-at / Gaze Direction）：记为 $\hat{g}$（从相机指向场景的单位向量，通常指向 - Z 轴方向）；
• 朝上方向（Up Direction）：记为 $\hat{t}$（垂直于观察方向的单位向量，通常指向 Y 轴方向，用于确定相机的 “左右”）。
  

  3️⃣ 视图变换矩阵的推导：两步实现

视图变换分为 “平移” 和 “旋转” 两步，最终矩阵为两步变换的组合（$M_{view}=R_{view}\cdot T_{view}$，先平移后旋转）。

• 第一步：平移相机到原点（$T_{view}$）
  • 将相机位置 $\vec{e}=(x_e,y_e,z_e)$ 平移到原点，场景中的所有点也随之平移相同的向量（抵消相机位置）：
  • 平移矩阵（4×4 齐次矩阵）：$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$
  • 效果：相机从 $\vec{e}$ 移动到 (0,0,0)，场景中任意点 $\vec{p}$ 变为 $\vec{p}-\vec{e}$。
• 第二步：旋转相机到标准方向（$R_{view}$）
  • 旋转的目标是让相机的 “观察方向 $\hat{g}$” 指向 - Z 轴、“朝上方向 $\hat{t}$” 指向 Y 轴，需要构造一个旋转矩阵 $R_{view}$。直接构造 $R_{view}$ 较复杂，可通过 “先求逆旋转矩阵 $R_{view}^{-1}$ ，再转置（正交矩阵的逆等于转置）” 实现：
  • 步骤 1：定义相机的局部坐标系基向量
    • 平移后，相机的局部坐标系由三个正交单位向量构成：$\hat{u}$（右方向）：$\hat{u}=\hat{t}\times \hat{g}$（朝上方向叉乘观察方向，确保与两者垂直）；$\hat{v}$（修正后的朝上方向）：$\hat{v}=\hat{g}\times \hat{u}$（确保严格垂直于观察方向和右方向）；$\hat{w}$（观察反方向）：$\hat{w}=-\hat{g}$（指向 - Z 轴，与标准方向一致）；
  • 步骤 2：构造逆旋转矩阵$R_{view}^{-1}$
    • $R_{view}^{-1}$的作用是 “将标准坐标系（X,Y,-Z）旋转到相机局部坐标系（$\hat{u},\hat{v},\hat{w}$）”，矩阵形式为：$R_{view}^{-1}=\left[\begin{array}{cccc}{\hat{u}}_x& {\hat{u}}_y& {\hat{u}}_z& 0\\ {\hat{v}}_x& {\hat{v}}_y& {\hat{v}}_z& 0\\ {\hat{w}}_x& {\hat{w}}_y& {\hat{w}}_z& 0\\ 0& 0& 0& 1\end{array}\right]$
  • 步骤 3：求$R_{view}$
    • 由于旋转矩阵是正交矩阵（行 / 列向量均为正交单位向量），其逆矩阵等于转置矩阵，因此：$R_{view}=(R_{view}^{-1}{)}^T=\left[\begin{array}{cccc}{\hat{u}}_x& {\hat{v}}_x& {\hat{w}}_x& 0\\ {\hat{u}}_y& {\hat{v}}_y& {\hat{w}}_y& 0\\ {\hat{u}}_z& {\hat{v}}_z& {\hat{w}}_z& 0\\ 0& 0& 0& 1\end{array}\right]$
• 视图变换的最终效果
  • 经过 $T_{view}$ 和 $R_{view}$ 后，相机处于：位置：原点 (0,0,0)；观察方向：指向 - Z 轴（$\hat{w}$ 方向）；朝上方向：指向 Y 轴（$\hat{v}$方向）；场景中的所有点也完成了对应的变换，为后续投影做好准备。
    

2.4 投影变换（Projection Transformation）：3D 到 2D 的 “拍照” 过程

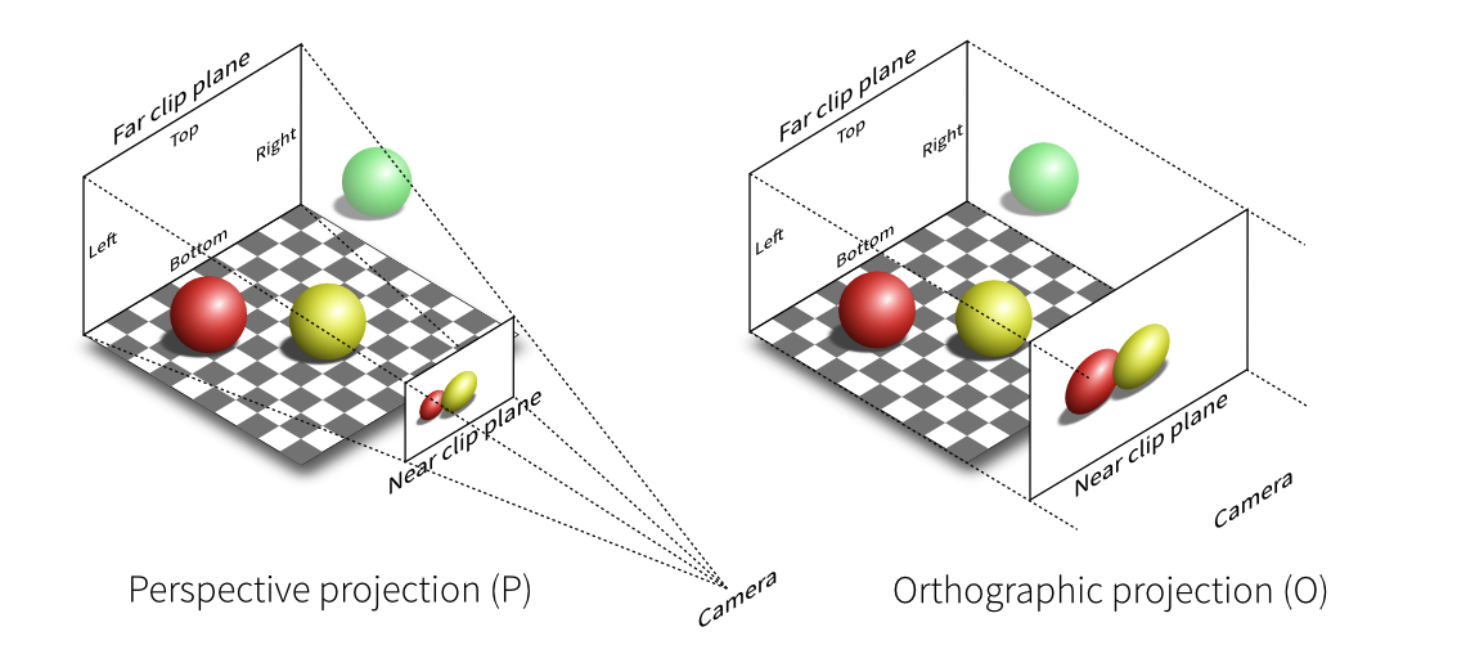
  投影变换是将 “相机视角下的 3D 场景” 转换为 2D 图像的核心步骤，图形学中主要分为两类：正交投影（Orthographic Projection） 和透视投影（Perspective Projection），前者适用于工程绘图，后者更符合人眼视觉规律（近大远小）。

2.4.1 正交投影（Orthographic Projection）

  正交投影的特点是 “所有投影光线平行”，物体的大小与距离无关，常用于建筑蓝图、CAD 设计等场景。

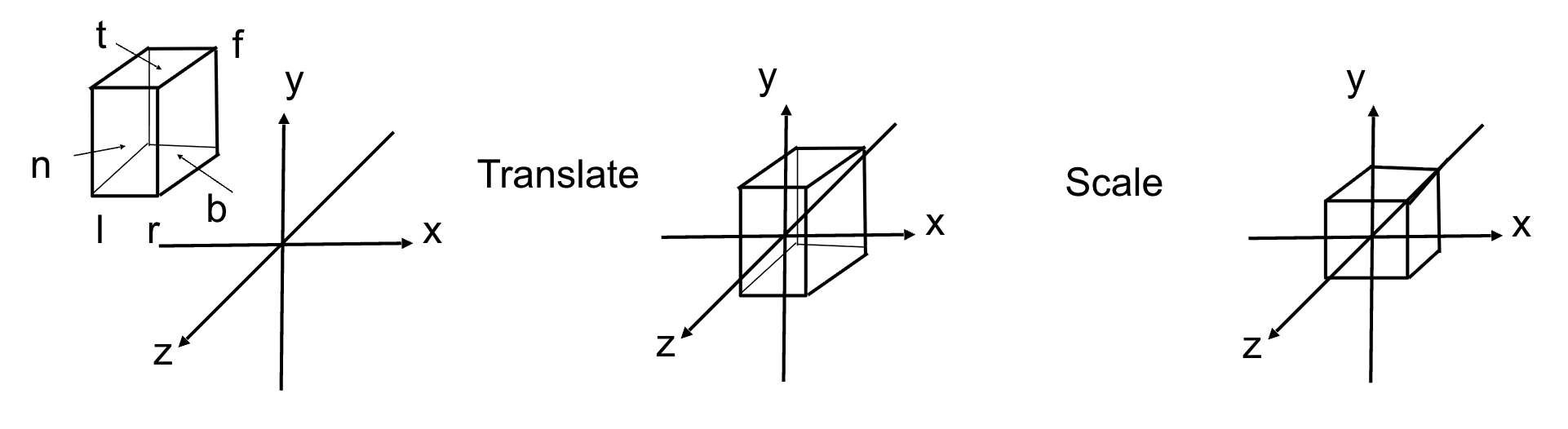
核心思想：将相机视角下的 3D 长方体区域（称为 “视景体”，定义为 $[l,r]\times [b,t]\times [f,n]$）映射到 “标准立方体” $[-1,1{]}^3$，步骤分为 “平移” 和 “缩放”：

• 视景体参数定义：$l/r$：x 轴方向的左 / 右边界；$b/t$：y 轴方向的下 / 上边界；$f/n$：z 轴方向的远 / 近平面（注意：由于相机看向 - Z 轴，近平面 n 的 z 坐标大于远平面 f，即 n > f ）；
• 变换目标：将长方体的中心移到原点，再缩放使各边长度为 2（适配标准立方体）。

正交投影矩阵 $M_{ortho}$：正交投影矩阵是 “平移矩阵” 与 “缩放矩阵” 的乘积（先平移后缩放）：$M_{ortho}=M_{scale}\cdot M_{translate}$。其中：

• 平移矩阵 $M_{translate}$：将视景体中心移到原点，抵消各轴的偏移：$M_{translate}=\left[\begin{array}{cccc}1& 0& 0& -\frac{l+r}{2}\\ 0& 1& 0& -\frac{b+t}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$
• 缩放矩阵 $M_{scale}$：将视景体各边缩放到长度为 2（x 轴缩放因子 $\frac{2}{r-l}$，y 轴 $\frac{2}{t-b}$ ，z 轴 $\frac{2}{n-f}$ ）：$M_{scale}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]$

关键注意点：正交投影无 “近大远小” 效果，因此不适合模拟人眼或相机的真实视觉；z 轴的缩放因子使用 $n-f$（而非 $f-n$），是因为 $n>f$，确保缩放后 z 坐标范围从 [f, n] 变为 [-1, 1]。

2.4.2 透视投影（Perspective Projection）

  透视投影是图形学中最常用的投影方式，符合人眼和相机的成像规律 —— 物体距离越远，在图像上的尺寸越小，平行直线会汇聚到消失点。

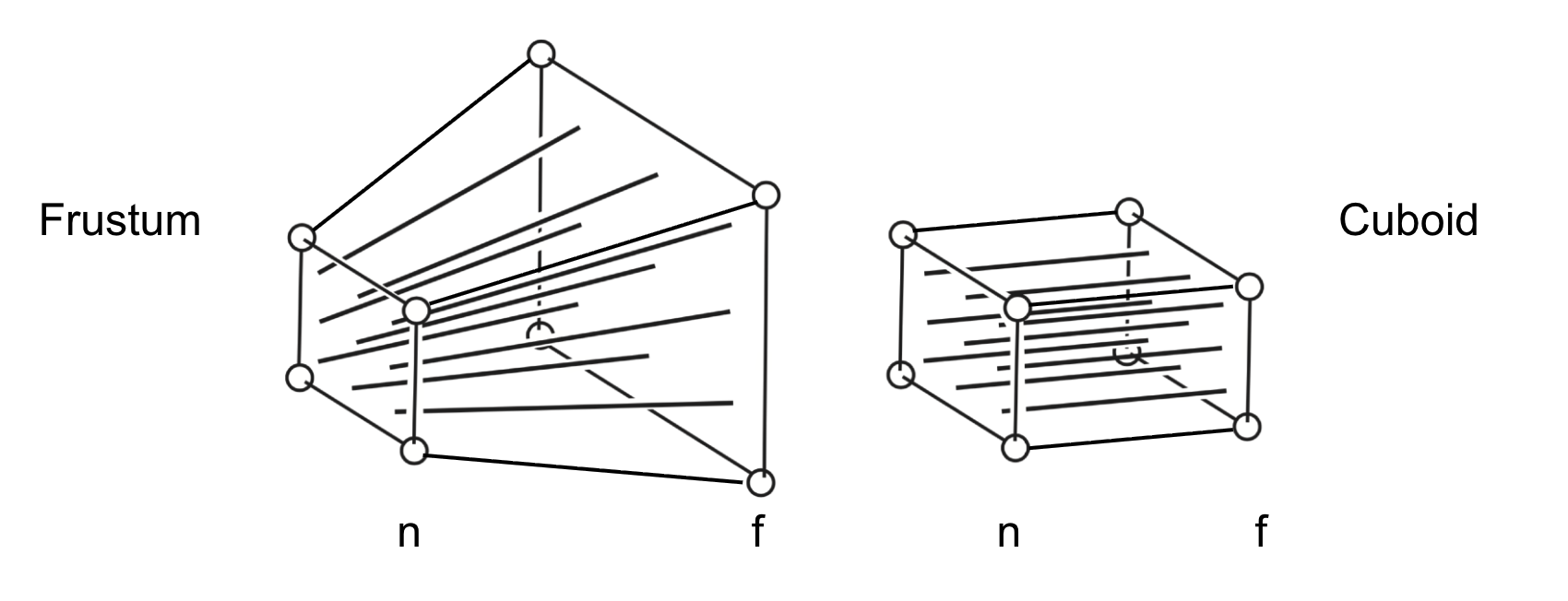
核心思想：两步实现透视投影的视景体是 “金字塔台”（称为 “视锥体”，近平面小、远平面大），无法直接用正交投影处理，因此分为两步：

• 第一步：挤压视锥体为长方体（$M_{persp\to ortho}$）：将视锥体沿 z 轴方向挤压，使近平面不变、远平面与长方体对齐；
• 第二步：执行正交投影（$M_{ortho}$）：用已有的正交投影矩阵处理挤压后的长方体；最终透视投影矩阵：$M_{persp}=M_{ortho}\cdot M_{persp\to ortho}$。
  

第一步推导：挤压矩阵 $M_{persp\to ortho}$ 挤压的核心依据是 “相似三角形”，需先找到挤压后点的坐标关系，再构造齐次矩阵。
① 相似三角形推导 x/y 坐标关系

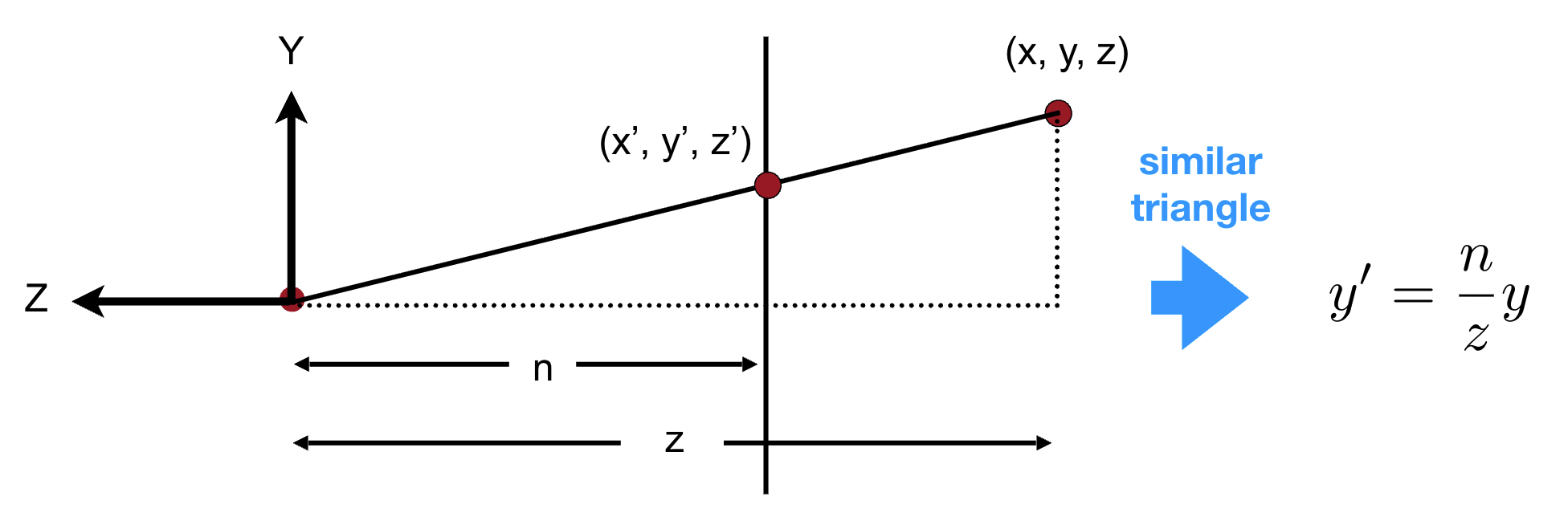
• 设视锥体内任意点 P = (x, y, z, 1)，近平面 z 坐标为n，远平面为f。根据相似三角形（从相机原点到近平面的投影），挤压后点 P’ 的 x/y 坐标为：$x^{\prime }=\frac{n}{z}\cdot x,y^{\prime }=\frac{n}{z}\cdot y$
• 逻辑：近平面上的点（ z = n ）挤压后 x/y 不变（x’ = x ），远平面上的点（z = f ）挤压后 x/y 缩小为 $\frac{n}{f}\cdot x$，符合 “近大远小”。
  

② 用齐次坐标表示挤压

• 由于 x’/y’ 包含 $\frac{1}{z}$（非线性项），需用齐次坐标将其转化为线性变换：将点 P = (x, y, z, 1) 的齐次坐标缩放 z 倍，得到 (n x, n y, ?, z) （其中 “?” 表示 z’ 的未知项），对应的挤压矩阵初步形式为：$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& A& B\\ 0& 0& 1& 0\end{array}\right]$。
• 关键：齐次坐标的 “缩放不变性”—— $(x,y,z,w)$ 与 $(kx,ky,kz,kw)$ 表示同一个 3D 点，因此缩放 z 倍后仍表示原有点。

③ 求解 z’ 的系数 A 和 B

• 挤压矩阵的第三行负责计算 z’，需利用 “近平面和远平面上的点挤压后 z 坐标不变” 这两个约束：
• 约束 1：近平面上的点（z = n）挤压后 z’ = n 取近平面上任意点 (0, 0, n, 1)，代入挤压矩阵得：$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\cdot \left[\begin{array}{c}0\\ 0\\ n\\ 1\end{array}\right]=An+B=n^2$。
• 约束 2：远平面上的点（z = f）挤压后 z’ = f 取远平面上任意点 (0, 0, f, 1)，代入挤压矩阵得：$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\cdot \left[\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right]=Af+B=f^2$。
• 解方程组：联立两个约束，解得 $A=n+f，B=-nf$。

④ 最终挤压矩阵

• $M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$

第二步：执行正交投影

• 将挤压后的长方体（视景体变为 $[l,r]\times [b,t]\times [f,n]$）代入正交投影矩阵 $M_{ortho}$，最终得到透视投影矩阵：$M_{persp}=M_{ortho}\cdot M_{persp\to ortho}$。

三、疑难点整理总结

待补充。

写在最后

  💗 感谢各位 📖 读者的支持，如果觉得文章对你有用，请 ♥️ 点赞 🌟 收藏，笔者将不胜感激 🌹～