数据结构与算法:倍增算法和ST表
前言
最近又开始flop了,cf掉大分,abc也开不出,补题也不想补,训练也不想训,甚至连博客都懒得写……感觉整个人都很急很烦,在烦各种各样的事,精力被牵扯掉好多……
一、倍增算法和ST表
1.基本原理
线段上有n个点,给定每个点i往右边跳1步能最远覆盖到的点jump[i],保证从任意点出发都能到达最后的点,且若i<j,必有jump[i]<=jump[j]。对于这个问题,考虑如何设计一张表,从而可以快速查询从任意点出发,跳1,2,4,8,……2^k步最远能到达的点,以及任意两点之间最少几步能到达。这张表,就是ST表。

定义st[i][p]为从i位置开始,往后跳2的p次方步能跳到的最远位置。那么st[i][0]肯定就直接等于jump[i],表示从i位置开始往后跳一步能到达的最远位置,然后st[i][p]就等于st[st[i][p-1]][p-1],表示先从i位置跳2的p-1次方步,然后从这个位置开始再跳2的p-1次方步,那么这就是从i位置开始跳2的p次方步能到的最远位置。

具体过程如上图例子,问从17开始跳几步能跳到77位置。那么首先因为77-17=60,所以在二进制中只需要考虑到第5位即可,因为2的6次方是64。那么就是从高位往低位考虑,若跳当前2的p次方步能到的最远位置大于等于77就不跳,否则就跳。
那么从17开始跳2的5次方步能到105,大于77,不跳。然后看从17开始跳2的4次方步能到49,小于77,那么就跳。然后从49开始往后跳2的3次方步能到94,大于77,不跳。从49开始跳2的2次方步能到79,大于77,不跳。之后从49开始往后跳2的1次方步能到70,小于77,那么就跳。然后从70开始往后跳2的0次方步能到73,小于77,那么就跳。最后,只需要从73位置再跳一步,就可以达到77了。
2.应用——国旗计划
#include <bits/stdc++.h>
using namespace std;/* /\_/\
* (= ._.)
* / > \>
*/typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;const int MAXN=2e5+5;
const int LIMIT=20;ll n,m;
vector<vector<ll>>line(MAXN<<1,vector<ll>(3));//小于等于n最接近的2的幂
int power;//ST表
vector<vector<int>>stjump(MAXN<<1,vector<int>(LIMIT));//返回小于等于n最接近的2的幂
int log2(ll n)
{int ans=0;while((1<<ans)<=(n>>1)){ans++;}return ans;
}void build()
{for(int i=1;i<=n;i++){if(line[i][1]>line[i][2]){line[i][2]+=m;}}sort(line.begin()+1,line.begin()+n+1,[](vector<ll>&x,vector<ll>&y){return x[1]<y[1];});//克隆for(int i=1;i<=n;i++){line[i+n][0]=line[i][0];line[i+n][1]=line[i][1]+m;line[i+n][2]=line[i][2]+m;}//初始化ST表int e=n<<1;for(int i=1,arrive=1;i<=e;i++){//找区间内最右开头while(arrive+1<=e&&line[arrive+1][1]<=line[i][2]){arrive++;}//跳一步能到的编号stjump[i][0]=arrive;}//构建ST表for(int p=1;p<=power;p++){for(int i=1;i<=e;i++){stjump[i][p]=stjump[stjump[i][p-1]][p-1];}}
}int jump(int i)
{//目标点int aim=line[i][1]+m;//当前位置int cur=i;//下一步int nxt=0;int ans=1;for(int p=power;p>=0;p--){nxt=stjump[cur][p];if(line[nxt][2]<aim){ans+=1<<p;cur=nxt;} }//跳的步数为ans+1,再+1才是线段条数return ans+1;
}void solve()
{cin>>n>>m;for(int i=1;i<=n;i++){line[i][0]=i;cin>>line[i][1]>>line[i][2];}//将环转成链,考虑在原来链的基础上多补一倍//那么对于[i,j],若i<j,就直接在原链上标记//若i>j,那么转化成[i,j+m]上标记//最后在补出来的链上把之前的标记重抄一遍//之后,因为线段之间不可能存在包含关系//所以对于每个线段,一步能到的最远线段肯定就是这个线段区间内最右线段//所以可以转化为问从i到i+m最少跳几次power=log2(n);build();vector<int>ans(n+1);for(int i=1;i<=n;i++){ans[line[i][0]]=jump(i);}for(int i=1;i<=n;i++){cout<<ans[i]<<" ";}cout<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve(); }return 0;
}还是最基本的一步,因为是环,那么就需要考虑将环转化成链,所以需要在原有的基础上多补一段。那么若对于一个人覆盖的范围[i,j],若i<j,那么就直接在原位置标记,否则就要在[i,j+m]上标记,最后在补出来的链上重抄一遍。之后,因为线段之间不可能存在包含关系,所以对于每个线段,一步能到的最远线段肯定就是这个线段的最右边界,所以问题就转化为求从i开始到i+m最少跳几步。
首先power记录小于等于n最接近的2的幂,所以每次只需要考虑到power即可。之后对数据进行预处理,那就是先根据左边界从小到大排序,然后抄一遍,最后找小于等于每个区间最右边界的最远左边界,那么这个编号就是一步能跳到的位置。所以之后对于每个编号i都去按照上述过程跳一遍即可,时间复杂度O(nlogn)。
二、ST表的更多应用
1.Balanced Lineup G
除了能到的最远位置,st表还可以维护区间最值。
当然,直接暴力线段树肯定能做()
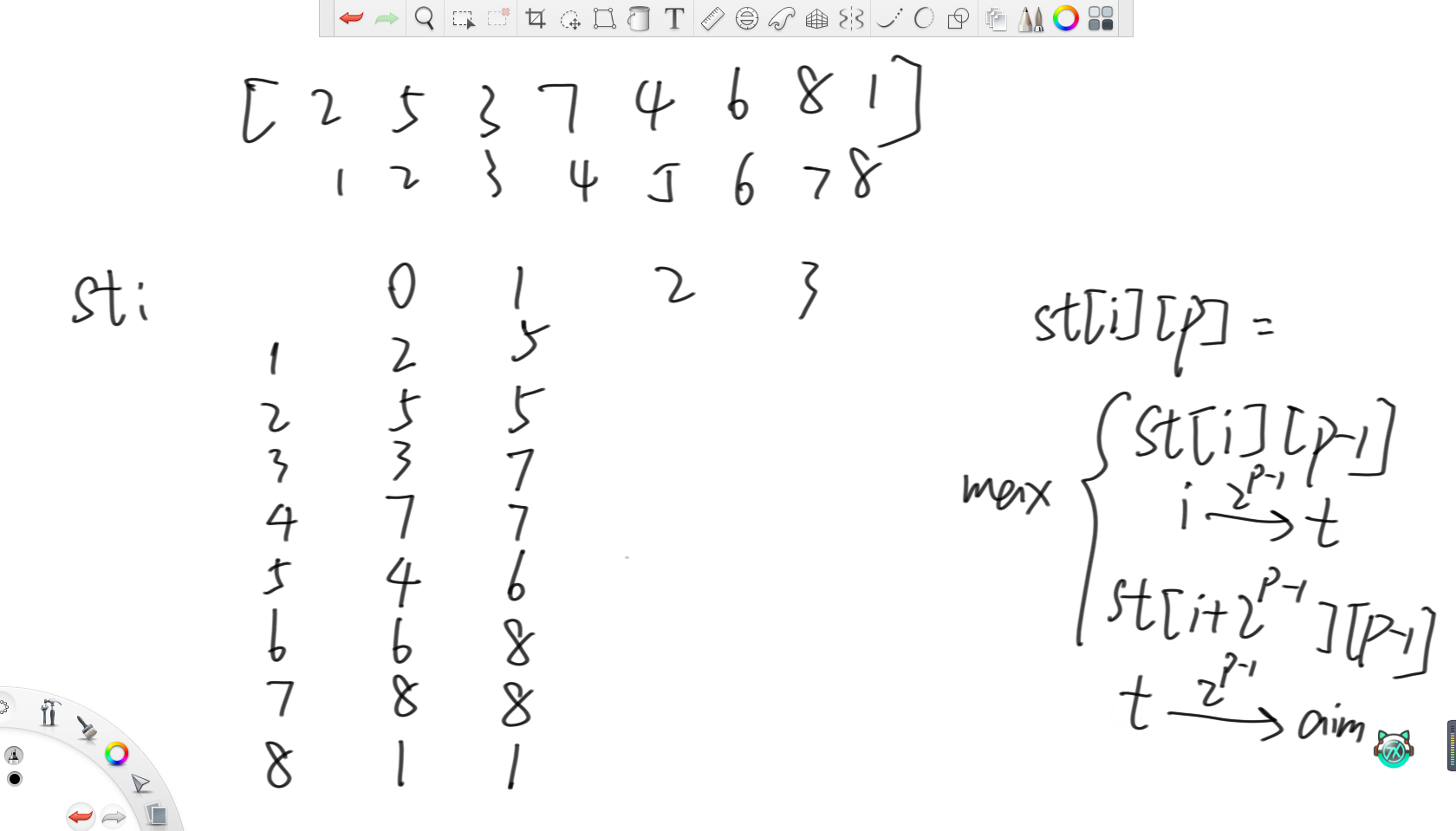
定义st[i][p]为从i位置开始往后2的p次方个位置的最大值,区间左闭右开。那么首先st[i][0]肯定就是自己,之后st[i][p]就等于st[i][p-1]和st[i+2的p-1次方][p-1]的最大值,就是从i位置开始跳2的p-1次方的最大值和从i+2的p-1次方开始跳2的p-1次方的最大值中的较大值。

对于17~37区间内的最大值,因为37-17+1=21,因为小于等于且最接近21的2的幂是2的4次方,那么就是st[17][4]和st[37-16=22][4]取最大值即可。
#include <bits/stdc++.h>
using namespace std;/* /\_/\
* (= ._.)
* / > \>
*/typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;const int MAXN=5e4+5;const int LIMIT=20;//快速查询<=i的最大的2的幂
vector<int>lg2(MAXN);//最大值
vector<vector<int>>stmax(MAXN,vector<int>(LIMIT));
//最小值
vector<vector<int>>stmin(MAXN,vector<int>(LIMIT));void build(int n,vector<int>&a)
{lg2[0]=-1;for(int i=1;i<=n;i++){lg2[i]=lg2[i>>1]+1;stmax[i][0]=a[i];stmin[i][0]=a[i];}for(int p=1;p<=lg2[n];p++){for(int i=1;i+(1<<p)-1<=n;i++){stmax[i][p]=max(stmax[i][p-1],stmax[i+(1<<(p-1))][p-1]);stmin[i][p]=min(stmin[i][p-1],stmin[i+(1<<(p-1))][p-1]);}}
}void solve()
{int n,q;cin>>n>>q;vector<int>a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}build(n,a);int l,r;while(q--){cin>>l>>r;int p=lg2[r-l+1];int a=max(stmax[l][p],stmax[r-(1<<p)+1][p]);int b=min(stmin[l][p],stmin[r-(1<<p)+1][p]);cout<<a-b<<endl;}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve(); }return 0;
}由于每个查询都要求小于等于长度且最接近的2的幂,所以考虑直接维护一个表出来。然后因为涉及区间最大最小值,所以要构建两个st表分别维护。
2.ST表的适用范围
通过上述例子不难发现,若A区间和B区间存在重叠的部分,但并不影响A+B区间的答案,就可以用ST表通过A区间答案+B区间答案整合出来。这种可重复贡献问题就可以考虑用ST表维护,比如最大最小值,区间gcd,区间与,区间或等问题,但像区间和等问题就不可以用ST表维护。
ST表相比线段树树状数组的优势就是构建时间复杂度O(nlogn),单次查询时间复杂度O(1),但缺点就是不支持修改操作。
3.gcd区间
#include <bits/stdc++.h>
using namespace std;/* /\_/\
* (= ._.)
* / > \>
*/typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;const int MAXN=1e3+5;const int LIMIT=10;vector<int>lg2(MAXN);vector<vector<int>>stgcd(MAXN,vector<int>(LIMIT));int gcd(int a,int b)
{return b==0?a:gcd(b,a%b);
}void build(int n,vector<int>&a)
{lg2[0]=-1;for(int i=1;i<=n;i++){lg2[i]=lg2[i>>1]+1;stgcd[i][0]=a[i];}for(int p=1;p<=lg2[n];p++){for(int i=1;i+(1<<p)-1<=n;i++){stgcd[i][p]=gcd(stgcd[i][p-1],stgcd[i+(1<<(p-1))][p-1]);}}
}void solve()
{int n,m;cin>>n>>m;vector<int>a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}build(n,a);int l,r;while(m--){cin>>l>>r;int p=lg2[r-l+1];int a=stgcd[l][p];int b=stgcd[r-(1<<p)+1][p];cout<<gcd(a,b)<<endl;}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve(); }return 0;
}这个题和上个题就很类似,观察一下就可以发现,只需要用st表维护区间gcd,每次查询对区间两部分的gcd再取一个gcd即可。
4.Frequent values
这个多测真的sb,没注意到WA了好几次……

因为是有序数组,所以其实可以考虑准备一个桶,去维护每个数出现的区间。那么若询问6~26区间内出现的词频,首先可以快速查出6位置对应的数是2,26位置对应的数是8。又因为2号桶的右边界是7,8号桶的左边界是25,所以6~7是2出现了2次,25~26是8出现了2次。所以,自然就可以知道中间都是3~7这些数,那么只需要用st表维护3~7范围上的词频最大值即可。
#include <bits/stdc++.h>
using namespace std;/* /\_/\
* (= ._.)
* / > \>
*/typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;const int MAXN=1e5+5;const int LIMIT=20;vector<int>lg2(MAXN);//维护桶的词频
vector<vector<int>>stmax(MAXN,vector<int>(LIMIT));//bucket[i]:i位置属于几号桶
vector<int>bucket(MAXN);
//L[i]:i号桶的左边界
vector<int>L(MAXN);
//R[i]:i号桶的右边界
vector<int>R(MAXN);void build(int n,vector<int>&a)
{a[0]=-1e9;int cnt=0;for(int i=1;i<=n;i++){if(a[i-1]!=a[i]){R[cnt]=i-1;L[++cnt]=i;}bucket[i]=cnt;}R[cnt]=n;lg2[0]=-1;for(int i=1;i<=cnt;i++){lg2[i]=lg2[i>>1]+1;//词频stmax[i][0]=R[i]-L[i]+1;}for(int p=1;p<=lg2[cnt];p++){for(int i=1;i+(1<<p)-1<=cnt;i++){stmax[i][p]=max(stmax[i][p-1],stmax[i+(1<<(p-1))][p-1]);}}
}void solve()
{while(true){int n;cin>>n;if(n==0){break;}int q;cin>>q;vector<int>a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}build(n,a);int l,r;while(q--){cin>>l>>r;//边界所在的桶的编号int lb=bucket[l];int rb=bucket[r];//属于同一个桶if(lb==rb){cout<<r-l+1<<endl;}else{//最左侧的桶在范围内有几个数int a=R[lb]-l+1;//最右侧int b=r-L[rb]+1;//中间个数int c=0;//中间有别的桶if(lb+1<rb){int s=lb+1;int e=rb-1;int p=lg2[e-s+1];c=max(stmax[s][p],stmax[e-(1<<p)+1][p]);}cout<<max(max(a,b),c)<<endl;}}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve(); }return 0;
}代码其实没啥好说的,就是离散化构建左右边界和桶的代码需要注意一下,byd昨天abc的d离散化给自己写晕了……
总结
加油加油!!
