【每天一个知识点】负二项分布(Negative Binomial Distribution, NB分布)
一、从“掷硬币”说起
假设我们在玩一个掷硬币的游戏,每次投掷出现正面(记作成功)的概率是 ( p )。
问题是:要想得到第3次正面,平均需要投多少次?
这类问题,其实就是负二项分布要解决的。
二、什么是负二项分布?
定义:
负二项分布(Negative Binomial Distribution)描述了这样一种随机现象:
当我们重复进行独立且成功概率相同的伯努利试验时,得到第 ( r ) 次成功所需的总试验次数 ( X ) 的概率分布。
通俗地说,它回答的是:
“我需要尝试几次,才能成功 ( r ) 次?”
三、公式长什么样?
若每次试验成功的概率是 ( p ),失败的概率是 ( 1-p ),那么
负二项分布的概率质量函数(PMF)为:
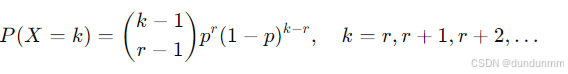
这里:
( X ):总试验次数;
( r ):成功次数(是固定的);
( k ):直到得到第 ( r ) 次成功所经历的总次数;
( p ):单次成功的概率。
四、举个栗子🌰
假设你掷一个公平硬币(( p = 0.5 )),想知道:
得到第 3 次正面需要掷 5 次的概率是多少?
代入公式:
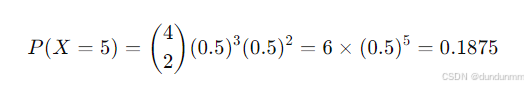
也就是说,大约 18.75% 的概率,你会在第 5 次投掷时获得第 3 个正面。
五、NB分布的两种常见“视角”
| 视角 | 描述 | 示例 |
|---|---|---|
| 次数视角 | 给定成功次数 ( r ),问要多少次试验 ( X ) 才能实现 | “我要得到第3次正面,需要掷几次?” |
| 失败视角 | 关注失败次数 ( Y = X - r ),即在第 ( r ) 次成功前失败了几次 | “得到第3次正面之前我失败了几次?” |
六、与几何分布的关系
几何分布(Geometric Distribution)其实是负二项分布的一个特例——当 ( r = 1 ) 时。
也就是说,
“为了第一次成功,需要多少次尝试?”
就是负二项分布的特殊情况。
七、NB分布与现实应用
虽然听起来像玩游戏,但负二项分布在现实统计与机器学习中非常有用。
📈 应用场景举例
| 领域 | 应用说明 |
|---|---|
| 生物统计 | RNA测序数据中基因表达计数服从NB分布(比泊松分布更能处理过度离散) |
| 工业质量控制 | 某零件在生产线上经过多少次检测才出现第 ( r ) 次不合格 |
| 市场营销 | 顾客购买行为分析,估计多少次点击后会产生第 ( r ) 次购买 |
| 医学研究 | 患者复发次数建模,或多少天后出现第 ( r ) 次症状 |
八、为什么叫“负二项”?
这个名字来自数学上的组合公式。
它源于二项式展开式:
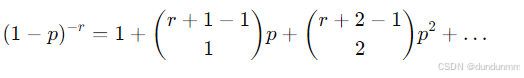
因为涉及负指数的二项展开,所以称为 “负二项”分布。
九、NB分布 vs. 泊松分布
| 特性 | 负二项分布 | 泊松分布 |
|---|---|---|
| 方差 | 通常大于均值(可建模“过度离散”) | 方差=均值 |
| 应用场景 | 计数型数据但波动较大 | 稳定计数数据 |
| 示例 | RNA-seq、顾客复购次数 | 每小时进站人数 |
这就是为什么在生物信息学中,RNA-seq计数数据几乎都用负二项分布建模。
十、小结 🧭
| 项目 | 内容 |
|---|---|
| 定义 | 重复独立试验中,获得第 ( r ) 次成功所需的试验次数分布 |
| 参数 | ( r ):成功次数;( p ):单次成功概率 |
| 特点 | 能处理“过度离散”的计数数据 |
| 典型场景 | 生物计数、营销事件、复发建模等 |
| 特殊情况 | ( r=1 ) 时即为几何分布 |
如果你想更深入了解,可以思考这样的问题👇
若成功率 ( p ) 很低(例如 0.01),负二项分布的尾部会不会变长?这说明了什么?
——提示:这正是它在建模稀疏、高方差数据(如基因计数)时大放异彩的原因。

