最优传输理论学习(1)+PINN文献阅读
2025.10.26周报
- 最优传输学习笔记(1)
- 什么是最优传输?
- 质量分布
- 质量守恒
- 成本函数
- Monge问题
- Monge的目标
- Monge的约束
- Monge问题的缺陷
- Kantorovich问题
- Kantorovich的目标
- Kantorovich的约束
- 线性规划
- Kantorovich的优势
- Wasserstein距离
- 为什么 WGAN 选用 W-1 距离?
- WGAN的优势
- 文献阅读
- 题目信息
- 摘要
- 创新点
- 网络架构
- 实验
- 结论
- 不足以及展望
最优传输学习笔记(1)
本周学习了最优传输的基本概念,并理解了Monge问题和Kantorovich问题,以及最优传输理论在WGAN中的应用。
什么是最优传输?
最优传输(Optimal Transport, OT) 要解决的问题其实可以用一个很生活的例子来理解:想象一下,面前有一堆山沙子第一个质量分布,记为 μ\muμ,你想把它们重新堆成一座城堡的形状第二个质量分布,记为 ν\nuν。
- μ\muμ 描述了沙子现在在哪里,以及每个地方有多少沙子。
- ν\nuν 描述了沙子 目标应该在哪里,以及城堡的每个位置需要多少沙子。

最优传输要解决的问题就是你该如何规划搬运这些沙子?
比如,从沙堆A点搬 xxx 公斤到城堡B点,从A点搬 yyy 公斤到城堡C点,才能使得总的“搬运成本”最低?
这个成本可以是你花费的力气,或者是搬运距离 ×\times× 沙子重量。
用一句话概括:最优传输就是研究如何用最少的代价将一个质量分布转为另一个质量分布。
质量分布
在数学上,一个质量分布就是一个测度空间 (X,μ)(X,\mu)(X,μ)。
空间 XXX:就是地点的集合。在沙堆的例子中,XXX 可以是地面,一个二维平面 R2\mathbb{R}^2R2。XXX 也可以是一维数轴 Rd\mathbb{R}^dRd。
测度 μ\muμ:这就是一个测量工具,即函数。你给它 XXX 空间中的一个区域AAA,它告诉你这个区域 AAA 里有多少“质量”。比如,μ(A)\mu(A)μ(A) 就是 AAA 区域里沙子的总重量。
所以,我们就有了两个测度空间 (X,μ)(X,\mu)(X,μ) 和 (Y,ν)(Y,\nu)(Y,ν) 来分别代表沙堆和城堡。
我们概率论中熟悉的概率分布其实就是一种特殊的质量分布。这是因为在概率论中,我们规定所有可能事件的概率之和(即“总质量”)必须等于 1。
最优传输则更通用,它可以处理总质量不为 1 的情况(比如你有 5 公斤沙子)。
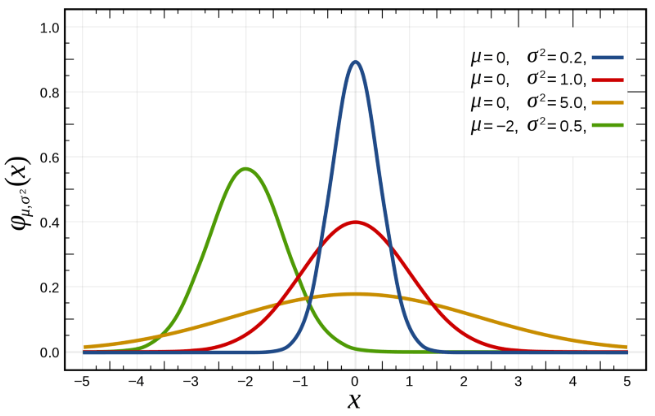
一维的标准高斯分布其实可以表示成 (R,μ)(\mathbb{R},\mu)(R,μ)
其中 μ((−∞,x])=12π∫−∞xe−x22dx\mu((-\infty,x]) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-\frac{x^2}{2}} dxμ((−∞,x])=2π1∫−∞xe−2x2dx。在这个测度空间中,我们要测量 (−∞,x](-\infty, x](−∞,x] 这个区域的“质量”,测量的方法就是计算标准高斯函数在这段区间上的积分。
质量守恒
一般情况下,质量不会凭空产生或消失。在沙堆的例子中,沙堆里沙子的总重量,必须等于城堡所需要的沙子的总重量。我们只是搬运,沙子不会变多也不会变少。我们会要求这两个分布的总质量是一样的,也就是 ∫Xdμ=∫Ydν\int_X d\mu = \int_Y d\nu∫Xdμ=∫Ydν。
但是也有不满足这个条件的情况。
比如在搬沙子的过程中,一部分沙子被风吹走了,这样质量减少了,或者你又从旁边铲了一些新沙子进来,这样质量增加。再比如在细胞数据中,细胞会随着时间生长或着死亡,细胞不同时间下的分布的质量肯定是不一样的,这个就是Unbalanced Optimal Transport (不平衡最优传输)。
成本函数
问题有了考虑的对象,我们还需要定义成本。我们定义一个成本函数 c(x,y):X×Y→R+c(x,y): X \times Y \rightarrow \mathbb{R}^+c(x,y):X×Y→R+。
它的意思是把 1 单位质量(比如 1 克沙子)从起点 xxx 点搬到终点 yyy 点所需要的成本。
最常见的成本函数就是距离,比如 c(x,y)=∣∣x−y∣∣c(x,y) = ||x-y||c(x,y)=∣∣x−y∣∣ 的欧氏距离,或者 c(x,y)=∣∣x−y∣∣2c(x,y) = ||x-y||^2c(x,y)=∣∣x−y∣∣2 的距离的平方。这意味着搬得越远,成本越高。
那如何去进行移动呢?
接下来主要有两个角度去考虑,分别是Monge问题 和Kantorovich问题。
Monge问题
Monge的思路非常直接,其试图寻找一个搬运计划 TTT,这个 TTT 是一个映射函数 为T:X→YT:X \rightarrow YT:X→Y。
这个 TTT 它告诉我们,从 XXX 空间里的每一个起点 xxx,你必须把它所带的质量搬到 YYY 空间里的某一个确定的终点 T(x)T(x)T(x)。这是一个“一对一”或“多对一”的确定性计划。
Monge的目标
Monge问题的目标是找到一个映射 TTT,使得总的搬运成本最低,用数学表达即为:
minT∫Xc(x,T(x))dμ(x)\min_T \int_X c(x, T(x)) d\mu(x)Tmin∫Xc(x,T(x))dμ(x)
- c(x,T(x))c(x, T(x))c(x,T(x)) 是把 xxx 处的质量搬到 T(x)T(x)T(x) 处的单位成本。
- dμ(x)d\mu(x)dμ(x) 代表 xxx 点附近无穷小区域的质量。
- ∫X\int_X∫X 就是把所有 xxx 点的搬运成本,比如 成本 ×\times× 质量 加起来,得到总成本。
我在网上看到一个非常容易理解的例子说清楚上述公式,把它讲清楚。
-
离散
空间 XXX ,代表起点:3个仓库位于 x1,x2,x3x_1, x_2, x_3x1,x2,x3。
质量分布 μ\muμ代表库存:
仓库 x1x_1x1 有 m1=10m_1 = 10m1=10 吨货物
仓库 x2x_2x2 有 m2=5m_2 = 5m2=5 吨货物
仓库 x3x_3x3 有 m3=20m_3 = 20m3=20 吨货物
空间 YYY (终点):3个商店位于 y1,y2,y3y_1, y_2, y_3y1,y2,y3。
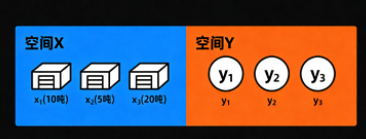
Monge问题目标:寻找一对一运输计划 TTT,将全部货物从仓库映射到商店。
成本函数 c(x,y)c(x, y)c(x,y):单位运输成本矩阵(如 c(x1,y1)=2c(x_1, y_1) = 2c(x1,y1)=2 元/吨)。运输计划 TTT:
T(x1)=y2T(x_1) = y_2T(x1)=y2,成本 7×10=707 \times 10 = 707×10=70 元
T(x2)=y3T(x_2) = y_3T(x2)=y3,成本 8×5=408 \times 5 = 408×5=40 元
T(x3)=y1T(x_3) = y_1T(x3)=y1,成本 3×20=603 \times 20 = 603×20=60 元
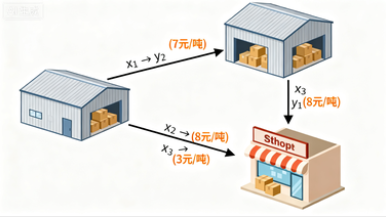
总成本:70+40+60=17070 + 40 + 60 = 17070+40+60=170 元
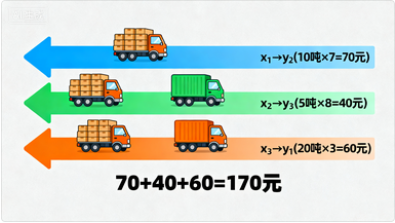
数学表达为:总成本=∑i=13c(xi,T(xi))×mi\text{总成本} = \sum_{i=1}^3 c(x_i, T(x_i)) \times m_i总成本=∑i=13c(xi,T(xi))×mi,目标是最小化所有可能的 TTT 组合的总成本。
-
连续
空间 XXX (起点):连续区域,如线段 [0,1][0, 1][0,1]。
质量分布 μ\muμ:密度函数 ρ(x)\rho(x)ρ(x) 描述沙子分布,dμ(x)=ρ(x)dxd\mu(x) = \rho(x) dxdμ(x)=ρ(x)dx 表示 xxx 处无穷小区域的质量。连续分布中单点质量为零,需通过积分计算总质量或成本。
Monge问题则是寻找运输映射 TTT 最小化连续形式的总成本:
总成本=∫Xc(x,T(x))dμ(x).\text{总成本} = \int_X c(x, T(x)) d\mu(x).总成本=∫Xc(x,T(x))dμ(x).
Monge的约束
这个映射 TTT 不能随便找,它必须满足一个约束,即搬运之后,沙堆 μ\muμ 必须正好变成城堡 ν\nuν。
这个约束被称为保测度条件,记为 T#μ=νT_{\#} \mu = \nuT#μ=ν。T#T_{\#}T# 是前推算子,用来描述 TTT 这个映射是如何把 μ\muμ 推成 ν\nuν 的。
这个保测度条件 T#μ=νT_{\#} \mu = \nuT#μ=ν 的数学定义是:
∀B⊂Y,ν(B)=μ(T−1(B))\forall B \subset Y, \nu(B) = \mu(T^{-1}(B))∀B⊂Y,ν(B)=μ(T−1(B))
其中:
BBB 是 YYY 空间中的任意一个区域,比如城堡的某个塔尖;
ν(B)\nu(B)ν(B) 是这个塔尖 BBB 需要的沙子质量;
T−1(B)T^{-1}(B)T−1(B) 是指 BBB 区域的来源地,即 XXX 空间中所有会被 TTT 映射到 BBB 区域的点的集合;
μ(T−1(B))\mu(T^{-1}(B))μ(T−1(B)) 是 TTT 计划从 T−1(B)T^{-1}(B)T−1(B) 搬过来的沙子总质量;
这个等式必须对所有区域 BBB 都成立,确保城堡的每个部分不多不少,正好接收到它所需的沙子。通俗地说,就是你从 XXX 搬多少重量的东西到 YYY 的某个区域,这个区域在 YYY 的度量下也得有这么多重量。
Monge问题的缺陷
Monge的映射 TTT 定义非常严格,它限制了我们不能实现"一对多"的操作。这个严格的映射定义就导致了一个很严重的问题,即Monge问题不一定有解。
为什么Monge无解?
因为它不允许你把 xxx 点的沙子分开,一部分送去 y1y_1y1,一部分送去 y2y_2y2。 Monge的映射 TTT 它只能对一个点 xxx 上的全部质量,指定一个新地点 T(x)T(x)T(x)。
狄拉克 →\rightarrow→ 高斯 这个任务,要求分解在 x0x_0x0 处的质量,把它分散到 YYY 空间中的无数个不同点上。
Monge的 TTT 在定义上就禁止这种分解和分散的操作。
它不能把 x0x_0x0 处的1kg质量,同时映射到 y1,y2,y3y_1, y_2, y_3y1,y2,y3。只能选一个。因此,不存在一个映射 TTT 能够满足 T#μ=νT_{\#} \mu = \nuT#μ=ν 这个保测度条件。
Kantorovich问题
Kantorovich 提出了一个更灵活的方案来解决Monge问题。核心思想是松弛。
其意思就是不再寻找一个一对一映射 TTT,而是寻找一个运输计划π\piπ。这个 π\piπ 是一个联合分布,其描述了“有多少质量从 xxx 搬运到了 yyy。
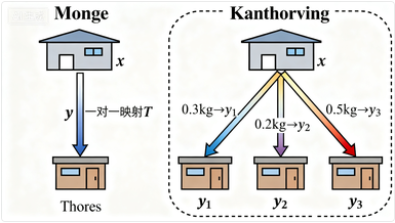
Kantorovich思想: 与Monge思想(xxx 处的 1kg 沙子 必须 100% 搬到 T(x)T(x)T(x) 点)不同。
Kantorovich思想中会使xxx处的 1kg 沙子可以分开搬运。这个计划 π\piπ 可能会xxx处的沙子,有 0.3kg搬到y1y_1y1点,0.2kg搬到y2y_2y2点,0.5kg 搬到y3y_3y3点。即实现一对多。
Kantorovich的目标
目标同样是最小化总成本,但现在是基于运输计划π\piπ 来计算:
minπ∫X×Yc(x,y)dπ(x,y)\min_{\pi} \int_{X \times Y} c(x,y) d\pi(x,y)πmin∫X×Yc(x,y)dπ(x,y)
其中:
dπ(x,y)d\pi(x,y)dπ(x,y) 代表从 xxx 搬到 yyy 的无穷小的质量。
∫X×Y\int_{X \times Y}∫X×Y 是对所有可能的起点-终点对 (x,y)(x,y)(x,y) 进行求和,即把单位成本 c(x,y)c(x,y)c(x,y) ×\times× 搬运的质量 dπ(x,y)d\pi(x,y)dπ(x,y)加起来。
Kantorovich的约束
这个计划 π\piπ 必须满足两个**边界分布 ** 约束
- Px#π=μP_x \# \pi = \muPx#π=μ
对于任何起点 xxx,从它那里运出去的总质量,比如对所有 yyy 求和,必须等于 xxx 原来的质量 μ(x)\mu(x)μ(x),即沙堆 xxx 处的沙子必须全部运走。 - Py#π=νP_y \# \pi = \nuPy#π=ν
对于任何终点 yyy,运抵它的总质量,比如对所有 xxx 求和,必须等于 yyy 需要的质量 ν(y)\nu(y)ν(y),即城堡 yyy 处收到的沙子必须刚好是它需要的量。
线性规划
这样的松弛之后,Kantorovich问题本质上变成了一个无限维的线性规划问题。为了更好地理解 π\piπ,我们可以想象一个离散情况。
假设区域 XXX 有 nnn 个仓库 x1,…,xnx_1, \dots, x_nx1,…,xn,库存分别为 aia_iai。
区域 YYY 有 mmm 个工厂 y1,…,ymy_1, \dots, y_my1,…,ym,需求分别为 bjb_jbj
那么运输计划 π\piπ 就变成了一个 n×mn \times mn×m 的矩阵 PPP。
PijP_{ij}Pij 就代表从 iii 仓库运到 jjj 工厂的货物量。
约束1 : ∑jPij=ai\sum_j P_{ij} = a_i∑jPij=ai ,行和,代表iii仓库的出货量等于其库存
约束2: ∑iPij=bj\sum_i P_{ij} = b_j∑iPij=bj ,列和,表示jjj工厂的收货量等于其需求
目标: min∑i,jCijPij\min \sum_{i,j} C_{ij} P_{ij}min∑i,jCijPij ,代表最小化总运输成本
这就是运筹学中非常经典的运输问题,是一个有限维的线性规划问题。
Kantorovich的优势
因为松弛允许了质量可分,我们总能找到一个最优搬运计划 π\piπ。线性规划告诉我们,如果耦合集合非空且紧,目标函数是下半连续的,那么线性规划一定可以取到最小值。也就保证了Kantorovich一定有解。这是它相较于Monge问题的最大优势。
Wasserstein距离
最优传输不仅能告诉我们怎么运,还能告诉我们两个分布 μ\muμ 和 ν\nuν 之间有多远。这个距离就是 Wasserstein 距离。
ppp-Wasserstein距离 WpW_pWp 的定义,几乎就是Kantorovich问题的最小值:
Wp(μ,ν)=(infπ∈U(μ,ν)∫X2d(x,y)pdπ(x,y))1/pW_p(\mu, \nu) = \left( \inf_{\pi \in U(\mu, \nu)} \int_{X^2} d(x,y)^p d\pi(x,y) \right)^{1/p}Wp(μ,ν)=(π∈U(μ,ν)inf∫X2d(x,y)pdπ(x,y))1/p
其中:
infπ∈U(μ,ν)\inf_{\pi \in U(\mu, \nu)}infπ∈U(μ,ν):在所有可能的运输计划 π\piπ 中,找到那个成本最低的。
∫X2d(x,y)pdπ(x,y)\int_{X^2} d(x,y)^p d\pi(x,y)∫X2d(x,y)pdπ(x,y):这就是总成本。
这里的成本函数 c(x,y)c(x,y)c(x,y) 被具体化为 d(x,y)pd(x,y)^pd(x,y)p,即两点 x,yx,yx,y 之间距离 ddd 的 ppp 次方。
所以,WpW_pWp 距离就是从一个分布转换为另一个分布所要付出的(最小)代价(的 1/p1/p1/p 次方)。
当 p=1p=1p=1 时,W1W_1W1 距离的成本函数就是 c(x,y)=d(x,y)c(x,y) = d(x,y)c(x,y)=d(x,y)(成本=距离)。W1W_1W1 也常被称为“推土机距离”(Earth-Mover’s Distance, EMD),因为它形象地表示了搬运沙土(质量)的最小代价。
为什么 WGAN 选用 W-1 距离?
这个距离有什么用呢?
了解生成模型的可能知道,WGAN 就是将W-1距离作为损失函数,解决了GAN训练不稳定的许多问题。主要是因为W-1度量比 KL散度 等度量具有更优良的性质。
举个例子理解一下:
假设 μ\muμ 是在 x=0x=0x=0 处的狄拉克分布(所有质量在0),ν\nuν 是在 x=1x=1x=1 处的狄拉克分布(所有质量在1)。这两个分布完全不重叠。
KL/JS散度会给出一个恒定的最大差异值,要么是无穷大,要么是一个恒定的最大值。如果你把 ν\nuν 移动到 x=1000x=1000x=1000,KL/JS散度值不变,它只知道不重叠,不知道差多远。
Wasserstein距离中W1(μ,ν)W_1(\mu, \nu)W1(μ,ν) 会计算把质量从 0 搬到 1 的成本,距离是1。如果你把 ν\nuν 移到 x=1000x=1000x=1000,W1(μ,ν)W_1(\mu, \nu)W1(μ,ν) 就会变成 1000。
WGAN的优势
GAN的目标是让生成器产生的数据分布 μ\muμ 尽可能接近数据分布 ν\nuν。W1W_1W1 距离更“弱”或更“平滑”。在训练初期,μ\muμ 和 ν\nuν 很可能完全不重叠。 W1W_1W1 能够告诉生成器虽然差,但是比上次进步了,比如距离从1000降到了950。这个梯度信号让训练更稳定。
而KL/JS只会表示还是不重叠,还是差,直接打个0分,导致梯度消失,训练不稳定。
文献阅读
题目信息
- 题目: Physics-Informed Neural Network Approach for Solving the One-Dimensional Unsteady Shallow-Water Equations in Riverine Systems
- 期刊: Journal of Hydraulic Engineering
- 作者: Zeda Yin, S.M.ASCE; Jimeng Shi; Linlong Bian, S.M.ASCE; William H. Campbell; Sumit R. Zanje, S.M.ASCE; Beichao Hu; and Arturo S. Leon, M.ASCE
- 发表时间: 2025
- 文章链接: https://ascelibrary.org/doi/epdf/10.1061/JHEND8.HYENG-13572
摘要
数值方法在求解非线性偏微分方程时,实际应用中存在一定困难。传统机器学习和深度学习模型依赖大量高质量训练数据,数据成本高且难度大。此外,这些模型多为黑箱模型,计算过程难以解释。尽管PINN近年来在多个领域取得成功,但在浅水方程及水文学和水力学领域的应用研究仍不充分。现有研究多集中于求解其他偏微分方程,且在考虑地形信息和摩擦的明渠水流问题上,尚无有效的PINN框架。基于以上背景,本论文提出一种新的PINN框架,为水系统工程问题提供更有效的解决方案。本论文的PINN框架,包括前向步骤、损失函数构建和反向步骤,还对其进行改进以解决大规模问题。通过两个案例验证,结果表明PINN能准确预测流速、流量和水位,且可进行位置和时间外推,但存在训练时间长和泛化性不足的局限。
创新点
该论文使用的PINN是无数据方法,不受数据获取难题限制。且PINN将物理规律数学表达式融入框架,能进行位置和时间外推,提升极端条件下可靠性。
网络架构
SVE由质量守恒方程和动量守恒方程组成,适用于任意形状的横截面,可写为:
∂U∂t+∂F∂x=S\frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} = \mathbf{S}∂t∂U+∂x∂F=S
其中,向量变量定义为:
U=[AQ],F=[QQ2A+gI1],S=[0gA(S0−Sf)]\mathbf{U} = \begin{bmatrix} A \\ Q \end{bmatrix}, \quad \mathbf{F} = \begin{bmatrix} Q \\ \frac{Q^2}{A} + g I_1 \end{bmatrix}, \quad \mathbf{S} = \begin{bmatrix} 0 \\ g A (S_0 - S_f) \end{bmatrix} U=[AQ],F=[QAQ2+gI1],S=[0gA(S0−Sf)]
A: 横截面湿周面积;Q: 横截面流量;gI1g I_1gI1 : 静水推力;SfS_fSf:摩擦坡度;S0S_0S0:地形高程坡度;t: 时间;x: 空间坐标。
其中:
g∂I1∂x=gA∂h∂xg \frac{\partial I_1}{\partial x} = g A \frac{\partial h}{\partial x}g∂x∂I1=gA∂x∂h
摩擦坡度通过Manning方程计算:
Sf=(nvKR0.667)2S_f = \left( \frac{n v}{K R^{0.667}} \right)^2Sf=(KR0.667nv)2
地形高程坡度为:
S0=−dzdxS_0 = -\frac{d z}{d x}S0=−dxdz
其中
n: Manning粗糙系数;v: 横截面流速;K: 单位转换因子;R: 水半径;z: 河床高程。
论文的PINN结构如下:
输入: 输入为空间x和时间t
输出: 为流速𝑣及水位h
结构: 全连接多层感知器,8个隐藏层,每层80个隐藏单元,ReLU激活函数。

由于横截面形状复杂,参数(A,P,R,B)无法解析计算。
论文基于DEM数据,采用数值方法计算。
DEM(Digital Elevation Model,数字高程模型)是一种表示地表高程的数字化数据集,通常以网格或点云的形式存储。
它记录了地表在特定位置(通常以经纬度或投影坐标表示)的海拔高度
广泛应用于地理信息系统、水文建模、地形分析、洪水模拟等领域。
DEM数据可以描述地形特征,如河床、坡度、山谷等,对于模拟水流、洪水传播和地形相关计算至关重要。
DEM提供离散采样点,每个点包含横截面距离a和高程b。
然后将高程值转换为相对于预测水深的坐标,如下图所示:

湿周面积A通过梯形规则积分高程和距离:
A=−∑i=1n−1(bi+1+bi)∗(ai+1−ai)2A = -\sum_{i=1}^{n-1} \frac{(b_{i+1} + b_i) * (a_{i+1} - a_i)}{2}A=−i=1∑n−12(bi+1+bi)∗(ai+1−ai)
湿周周长P累加相邻点间的欧几里得距离:
P=∑i=1n−1(ai+1−ai)2+(bi+1−bi)2P = \sum_{i=1}^{n-1} \sqrt{(a_{i+1} - a_i)^2 + (b_{i+1} - b_i)^2}P=i=1∑n−1(ai+1−ai)2+(bi+1−bi)2
水面半径R和顶部宽度B直接从A,P和边界点计算:
R=APR = \frac{A}{P}R=PA
B=am−akB = a_m - a_kB=am−ak
损失函数: 损失函数包括上游边界、下游边界、质量方程和动量方程损失组成。
由于各部分量级差异,比如,水位h为102而偏导数∂h∂t\frac{\partial h}{\partial t}∂t∂h为10-3-10-8,直接求和会导致优化偏向某些分量。每个损失分量乘以权重(W1−W4W_1 −W_4W1−W4),使其量级接近,权重通过边界条件的量级和网格划分,如下图所示:

Ltotal=W1Lupbc+W2Ldownbc+W3Lphysicsmass+W4Lphysicsmomentum\mathcal{L}_{\text{total}} = W_1 \mathcal{L}_{\text{up}_{bc}} + W_2 \mathcal{L}_{\text{down}_{bc}} + W_3 \mathcal{L}_{\text{physics}_{mass}} + W_4 \mathcal{L}_{\text{physics}_{momentum}}Ltotal=W1Lupbc+W2Ldownbc+W3Lphysicsmass+W4Lphysicsmomentum
PDE残差项基于SVE:
Lphysics=1Nphysics∑i=1Nphysics∣∂U∂t+∂F∂x−S∣2\mathcal{L}_{\text{physics}} = \frac{1}{N_{\text{physics}}} \sum_{i=1}^{N_{\text{physics}}} \left| \frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} - \mathbf{S} \right|^2Lphysics=Nphysics1i=1∑Nphysics∂t∂U+∂x∂F−S2
上游边界条件损失:
Lupbc=1Nupbc∑i=1Nupbc∣v^bc−vbc∣2\mathcal{L}_{\text{up}_{bc}} = \frac{1}{N_{\text{up}_{bc}}} \sum_{i=1}^{N_{\text{up}_{bc}}} \left| \hat{v}_{bc} - v_{bc} \right|^2Lupbc=Nupbc1i=1∑Nupbc∣v^bc−vbc∣2
下游边界条件损失:
Ldownbc=1Ndownbc∑i=1Ndownbc∣h^bc−hbc∣2\mathcal{L}_{\text{down}_{bc}} = \frac{1}{N_{\text{down}_{bc}}} \sum_{i=1}^{N_{\text{down}_{bc}}} \left| \hat{h}_{bc} - h_{bc} \right|^2Ldownbc=Ndownbc1i=1∑Ndownbch^bc−hbc2
其中:
Nphysics{N_{\text{physics}}}Nphysics为配点总数;Nupbc{N_{\text{up}_{bc}}}Nupbc与Ndownbc{N_{\text{down}_{bc}}}Ndownbc上下游边界点数;W1−W4W_1 −W_4W1−W4为权重;
实验
实验采用多阶段训练策略,如下图所示:
分阶段优化边界和物理方程,模拟了先确定边界再求解内部场的逻辑,加速收敛。论文将训练分为三个阶段优化。
- 第一阶段为放大边界条件权重,优先优化边界收敛。
- 第二阶段则平衡权重,降低学习率,优化SVE残差。
- 第三阶段略微增加SWEs权重,进一步提高精度。

论文通过假设和实际场景研究展示了PINN框架求解一维非定常浅水方程的性能,具体结果如下:
-
假设的均匀梯形渠道中流量和水位突然变化的场景
PINN框架和HEC - RAS输出的速度和水位剖面吻合良好,所有横截面速度和水位的平均绝对误差分别为0.002743 m/s和0.001219 m。

PINN能高精度求解流量基一维浅水方程,预测水位的平均绝对误差与速度基PINN相近,约为0.0012 m,但流量的平均绝对误差比速度大,这是因为流量尺度更大且未进行归一化。

-
休斯顿赛普拉斯溪下游的实际案例
PINN框架和HEC - RAS输出对比,流量预测的平均绝对误差在0.0833 - 0.10083 m³/s之间,水位预测的平均绝对误差在0.0152 - 0.079 m之间,PINN输出趋势对流量和水位略有低估。

通过追踪内部横截面在每次迭代中的损失函数值,发现存在全局最小值,证明PINN框架理论上可获得一维浅水方程的小残差解。

PINN在计算域内的位置外推结果准确,平均绝对误差甚至小于非外推预测结果。

在计算域外进行外推测试,与边界位置的结果无显著差异,表明PINN可在域外进行合理外推。

以水位站记录的历史数据为参考,对未来30小时进行外推,外推结果的平均绝对误差与非外推预测相似,趋势与历史曲线拟合良好。

结论
本文提出并测试了用于求解SVE的物理信息神经网络。PINN框架能准确预测假设场景和历史洪水场景结果,误差小。可求解基于速度和流量的浅水方程,能对下游赛普拉斯溪案例在大流量下准确预测流量和水位。实验结果表明PINN理论上可获小残差解,还能进行位置和时间外推,与参考数据高度吻合。
不足以及展望
PINN训练时间长,因优化器找最优解难,且本文方法集成数值计算,GPU处理表现差。且PDE在边界和初始条件不确定时有无限解,PINN只能在特定边界条件下求近似解,不同条件需重新训练。后续希望探索优化训练算法或硬件加速方式,减少PINN训练时间,如改进GPU对数值计算的处理能力。
