当前位置：首页 > news >正文

opencv学习笔记6：SVM分类器

news 2025/10/25 16:38:31

一.SVM的感性认识

1.什么是 SVM 分类器？

2.核心概念：用通俗例子理解

1. 什么是 "超平面"？

2. 什么是 "支持向量"？

3. 为什么要 "最大间隔"？

3.处理复杂情况

1. 数据分不开怎么办？-核函数（非线性问题）

2. 有杂音怎么办？（软间隔）

4.SVM 的优缺点（大白话版）

优点：

缺点：

5.一句话总结

二.正式介绍

1.概念

支持向量与分类超平面示例：

2.什么是线性分类器？

3.核心思想

三.b站课程算法详解

四.标准公式化讲解

1. 超平面的数学表达

2. 间隔的定义与最大化

（1）距离公式

（2）两侧最近样本的距离公式

更详细的解释为什么是1和-1？————————————————————————

（3）目标：最大化间隔

3. 支持向量的作用

一.SVM的感性认识

如果你是机器学习零基础，我们可以用更通俗的方式来理解 SVM 分类器，避免复杂的数学概念。

1.什么是 SVM 分类器？

SVM（Support Vector Machine，支持向量机）本质上是一种 "找最佳分割线" 的算法，目的是把不同类别的数据分开。

想象一个场景：

你有一堆红苹果和绿苹果（两种数据）
你想画一条线，把红苹果和绿苹果完全分开
SVM 的作用就是帮你找到这条 "最好" 的线

2.核心概念：用通俗例子理解

1. 什么是 "超平面"？

在二维平面（比如一张纸）上，就是一条直线
在三维空间（比如一个盒子）里，就是一个平面
简单说：用来分隔不同类数据的边界

2. 什么是 "支持向量"？

假设你已经画了一条分隔线：

红苹果中离这条线最近的那个苹果
绿苹果中离这条线最近的那个苹果这两个苹果就是 "支持向量"，它们决定了这条线的位置。

3. 为什么要 "最大间隔"？

SVM 的核心是找 "最大间隔" 的线：

间隔 = 分隔线到两边最近苹果的距离之和
最大间隔的意思是：让这条线离两边最近的苹果都尽可能远

为什么要这样做？比如有两条线都能分开红、绿苹果：

线 A 离红苹果很近，离绿苹果也很近
线 B 离两边苹果都很远显然线 B 更好，因为如果再来一个稍微靠近边界的新苹果，线 B 更不容易分错（抗干扰能力强）

3.处理复杂情况

1. 数据分不开怎么办？-核函数（非线性问题）

有时候红苹果和绿苹果混在一起，比如红苹果在中间，绿苹果在外面围成一圈，直线肯定分不开。

SVM 的解决办法：核函数

可以理解为 "把数据掰弯" 的工具
比如把二维平面的数据 "掰" 成三维的，原本在二维里绕在一起的点，在三维里可能就分开了
常见的 "掰弯" 方式有：线性（不掰弯）、径向基（适合大部分复杂情况）、多项式等

2. 有杂音怎么办？（软间隔）

实际数据中常有 "捣蛋鬼"：比如一个红苹果跑到绿苹果堆里了。

SVM 的解决办法：允许少量错误

通过参数 C 控制 "严格程度"
C 值大：不允许犯错，哪怕线歪一点也要把所有苹果分开（可能过拟合）
C 值小：允许少数苹果站错队，保证大部分苹果分得清楚（更稳健）

4.SVM 的优缺点（大白话版）

优点：

效果好：尤其是数据维度高（比如文本分类，特征很多）但样本不多的时候
稳健：不容易被个别异常数据带偏
灵活：能处理直线分不了的复杂数据

缺点：

慢：数据太多时，训练起来费劲
挑参数：要试不同的 "掰弯" 方式和严格程度，才能找到最佳效果
不擅长多分类：原生只能分两类，要分多类（比如苹果、香蕉、橘子）需要特殊处理

5.一句话总结

SVM 是一个 "追求完美分割线" 的算法，它找到的线不仅能分开数据，还会尽可能远离两边的数据，遇到复杂情况还能 "掰弯" 空间来处理，适合中小规模、特征多的分类任务。

如果想动手试试，前面提到的代码例子可以直接运行，只需要安装 scikit-learn 库（pip install scikit-learn），就能直观看到 SVM 如何工作了。

二.正式介绍

1.概念

SVM（Support Vector Machine，支持向量机），SVM本质模型是特征空间中最大化间隔的线性分类器，是一种二分类模型。其核心思想是在特征空间中找到一个最优超平面，将不同类别的样本分隔开，且使这个超平面与两侧最近样本（支持向量，支持向量就是离分类超平面（Hyper plane）最近的样本点）的距离（即 “间隔”）最大化。

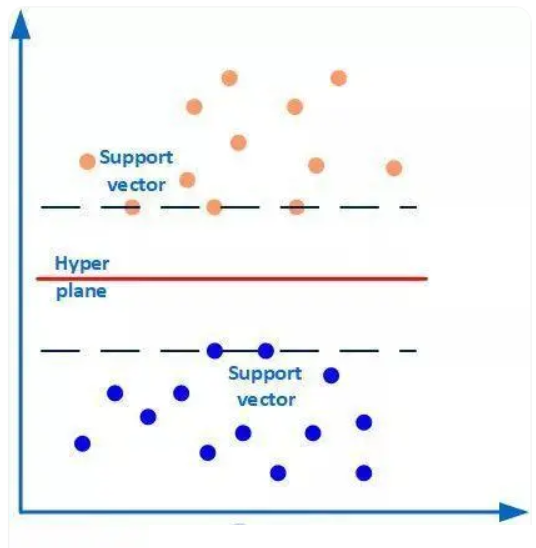
支持向量与分类超平面示例：

如下图所示，有两类样本数据（橙色和蓝色的小圆点），中间的红线是分类超平面，两条虚线上的点（橙色圆点3个和蓝色圆点2个）是距离超平面最近的点，这些点即为支持向量（坐标点本身就是向量）。简单地说，作为支持向量的样本点非常非常重要，以至于其他的样本点可以视而不见。而这个分类超平面正是SVM分类器，通过这个分类超平面实现对样本数据一分为二。

2.什么是线性分类器？

SVM是一种线性分类器，分类的对象要求是线性可分。因此我们首先要了解什么是线性可分与线性不可分。

假如在课桌“三八线”的两旁分别放了一堆苹果和一堆荔枝，通过“三八线”这样一条直线就能把苹果和荔枝这两种类别的水果分开了（如左下图），这种情况就是线性可分的。但是如果苹果和荔枝的放置位置是苹果包围荔枝的局面（如右下图），就无法通过一条直线将它们分开（即这样的直线是不存在的），这种情况则是线性不可分的情形。当然，这里举例的对象是苹果、荔枝等具体实物。在机器学习上，学习分类的对象则转化为一系列的样本特征数据（比如苹果、荔枝的相关特征数据，形状、颜色等）。

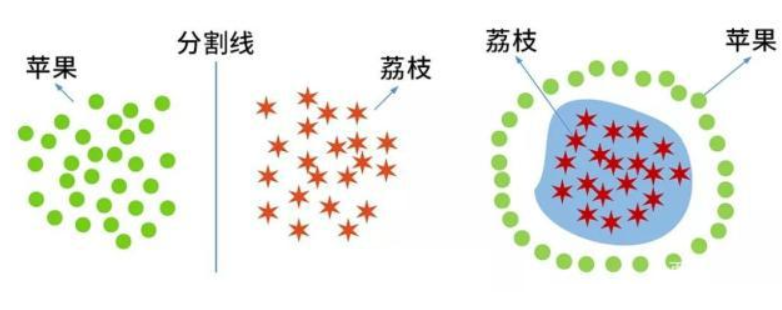
因此，只有当样本数据是线性可分的，才能找到一条线性分割线或分割面等，SVM分类才能成立。假如样本特征数据是线性不可分的，则这样的线性分割线或分割面是根本不存在的，SVM分类也就无法实现。

在二维的平面课桌上，一条直线就足以将桌面一分为二。但如果扩展到三维空间中，则需要一个平面（比如一面墙、一扇屏风等）才能将立体空间区域一分为二。而对于高维空间（我们无法用图画出），能将其一分为二的则称为超平面。

对于不同维度空间，SVM的形式特点也不同，具体表现如下：

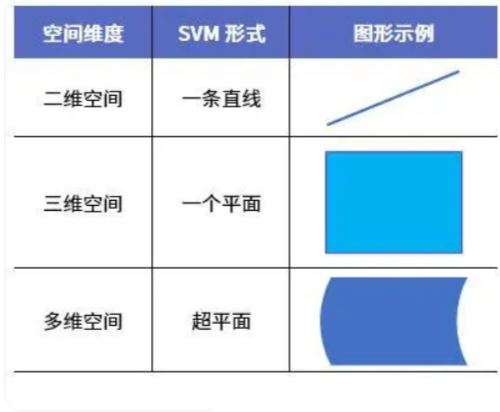
3.核心思想

SVM的核心是在特征空间中寻找一个超平面，使得:

1.该超平面能将不同类别的样本“千净”地分隔开(二分类场景);
2.超平面与两侧最近样本的距离(即“间隔")最大化。二维空间中，两类点之间可能有无数条分隔直线，但 “正中间” 那条距离两侧最近点最远的直线，是最稳健的选择。

三.b站课程算法详解

b站课程强烈推荐：

【【学习笔记】SVM】 https://www.bilibili.com/video/BV1r44y1q7be/?share_source=copy_web&vd_source=c5e7aba5c7851f39874c555b41af81df

1.

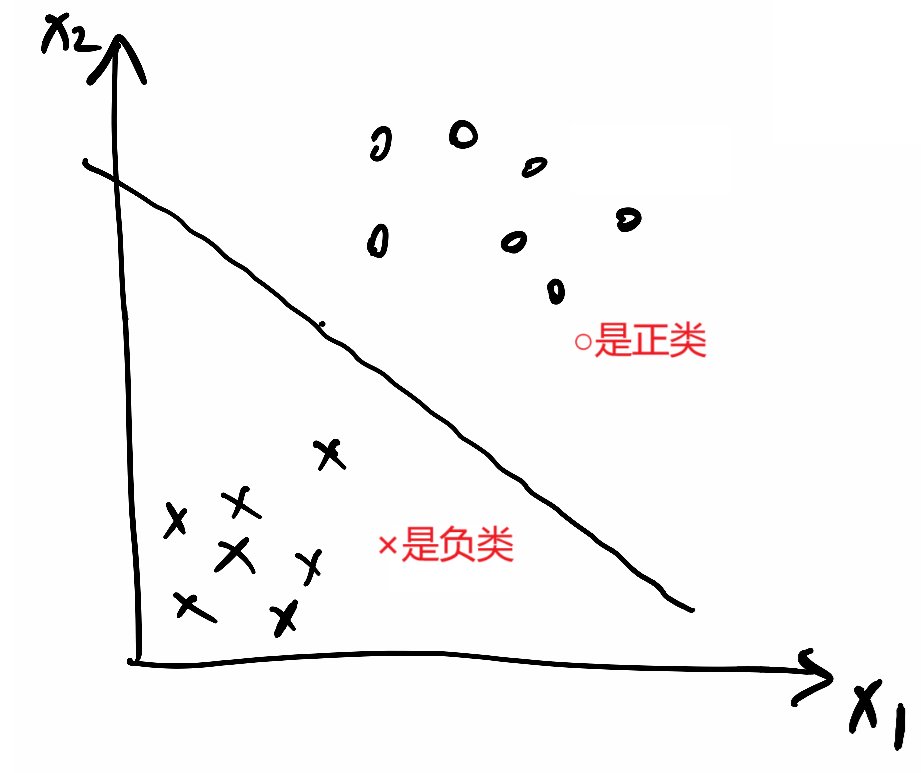①x和y坐标形式写成x1和x2形式，则分割线公式：a1·x1 + a2·x2 + b = 0
②写成向量形式：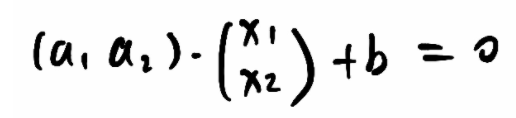
③又可以写成 wᵀ·x+b=0 ，w和x就是上面的竖向量

2.

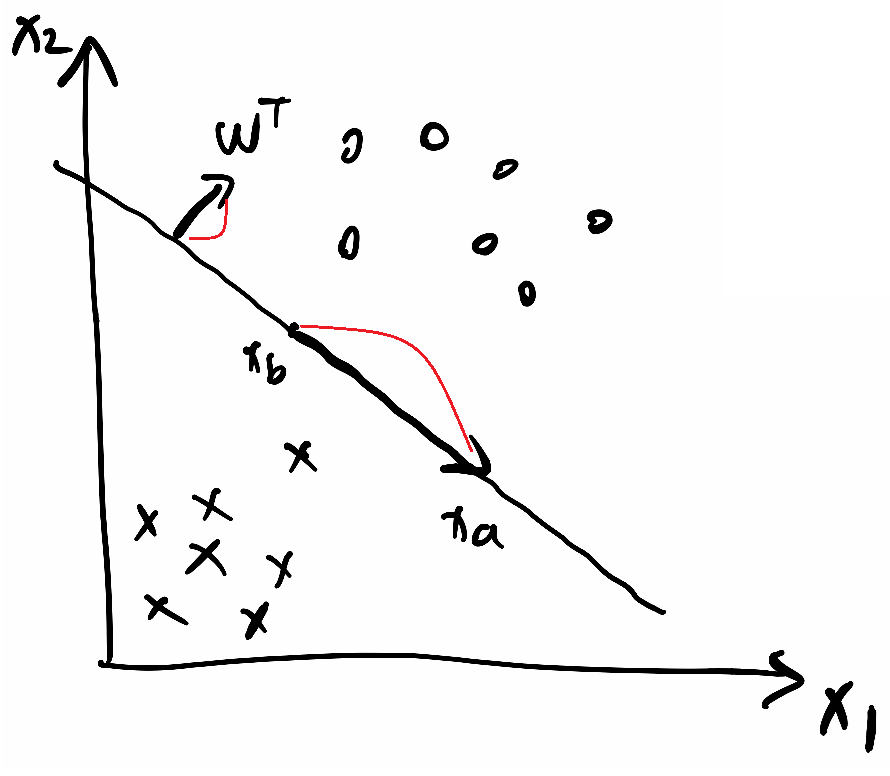①wᵀ·x+b=0是分割线
②假设分割线上两个点坐标为xa和xb，代入分割线式子，
wᵀ·xa+b=0③
wᵀ·xb+b=0④
③④相减得到wᵀ·(xa-xb)=0⑤
⑤这个式子中xa-xb两个点相减就是分割线上的一个向量，而点积为0，说明wᵀ与该向量垂直，即说明wᵀ是这个分割线/超平面的法向量

3.

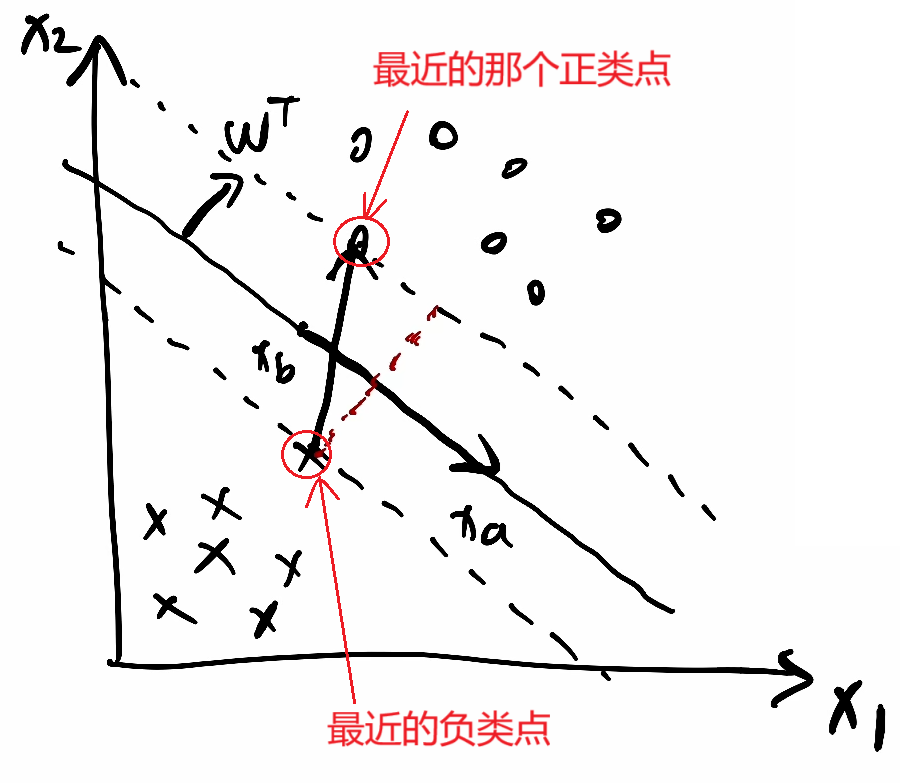①把分割线向上平移接触到第一个正样本点时停下，标上虚线；把分割线向下平移接触到第一个正样本点时停下，标上虚线
②假设第一个正样本点设为xp；第一个负样本点设为xr，代入
上面的正样本点虚线方程为：wᵀ·xp+b=k
下面的负样本点虚线方程为：wᵀ·xr+b=-k
为了简化计算，我们可以把k除到前面的系数里面，不影响整体直线方程因此得到两条简化的虚线方程：
wᵀ·xp+b=1
wᵀ·xr+b=-1
两式相减wᵀ·(xp-xr)=2，xp-xr可以看成是从点xr指向xp的一个向量
③此式两边同除上 $\l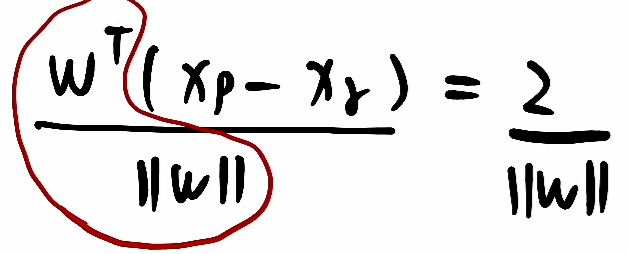eft \| w \right \|$ 得：，前面红圈里向量除自己的模就是该方向的单位向量，则xp-xr这个向量乘上单位向量，就是在该单位向量上的一个投影，即图中红色虚线这个向量。
④该投影就是最大间隔，那他取最大，就得让 $\left \| w \right \|$ 取最小，计算 $\left \| w \right \|$ 的最小值，为了便于求导，就去计算1/2 · $\left \| w \right \|$ ²的最小值，通过拉格朗日对偶性和KKT 条件将问题转化为更易求解的形式，最终确定超平面参数w和b。

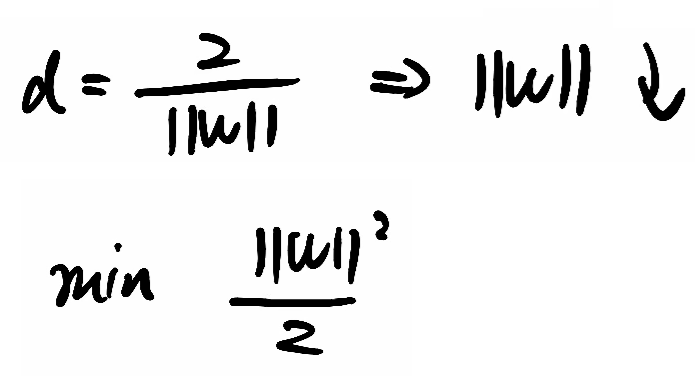
四.标准公式化讲解

1. 超平面的数学表达

这里的+1和-1完全可以替换成任意常数k和-k（解释在下面的2(2) ）

2. 间隔的定义与最大化

间隔（Margin） 指超平面到两侧最近样本的距离之和。

（1）距离公式

↑上面的这个点到面距离可以类比点到线距离公式推出来↓

（2）两侧最近样本的距离公式

w · x + b = 0 是中间的分割线（在三维中就是超平面），而w · x + b ≥ 1 说明在线w · x + b = 1上侧的是正类样本，即在分割线w · x + b = 0上侧距离该分割线距离大于等于 $\frac{1}{\left \| w \right \|}$ 的位置是正类样本（带入点到线/点到面的距离公式可得 $\frac{1}{\left \| w \right \|}$ ，把上面(1)的di上面带入w · x + b = 1，计算可得di= $\frac{1}{\left \| w \right \|}$ ）
w · x + b ≤ 1，意思是在分割线下侧距离该分割线距离大于等于 $\frac{1}{\left \| w \right \|}$ 的位置是负类样本。