pfc性能优化_占空比前馈优化
前言
引入参考电流校正,以修正DCM 模式下采样电流值为电感电流平均
值,但是仍然存在轻载工况下输入电流畸变严重,THD 较大的问题。一般会在PFC控制系统上加入一个占空比前馈环节,当PFC 在宽输出功率下工作,即同时存在DCM 模式与CCM 模式,此时单一的占空比前馈方案不再适用。如果对传统的占空比前馈方案加以改进,使得PFC 系统在宽输出功率下都有较低的输入电流THD,并从输入导纳的角度分析占空比前馈方案的合理性。
1.DCM 与CCM 临界条件分析
为了使得PFC 系统能够在全负载下稳定运行,首先需要分析DCM 模式与CCM模式的临界工作点,下面推导DCM 模式与CCM 模式的临界条件。
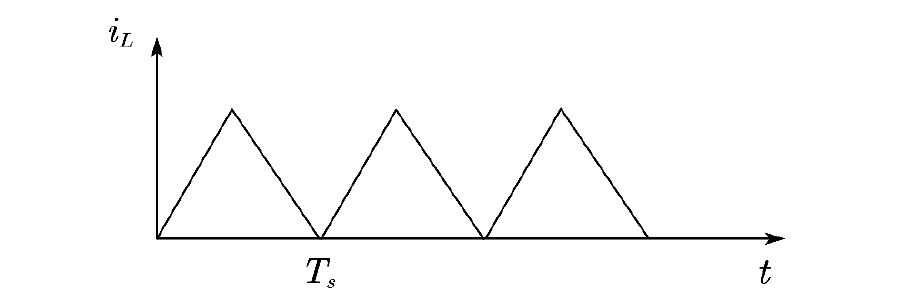
临界电流模式电感电流波形如图所示,电感电流采样值等于电感电流平均值,设开关周期为,那么电感电流采样值为:
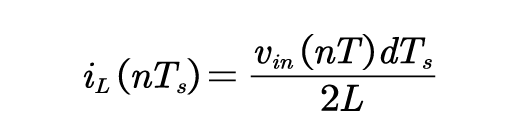
因为电流环带宽远大于电压环带宽,输入导纳可以近似为常量,所以有:
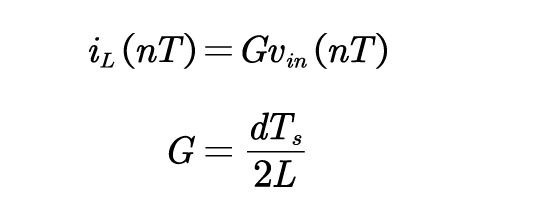
当PFC 工作于临界点时,在单个开关周期内占空比为:
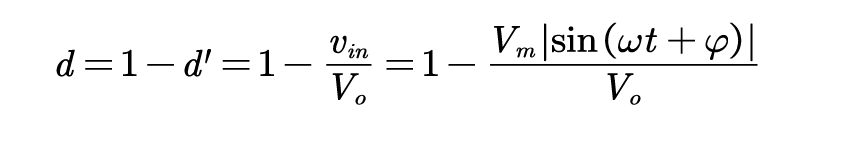
所以临界导通时输入导纳为:
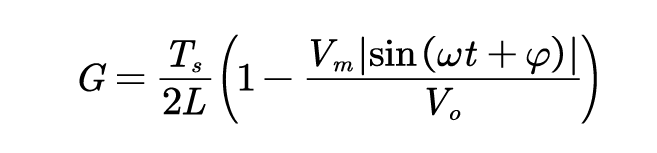
若PFC 在整个工频周期都工作于CCM 模式,需满足条件:
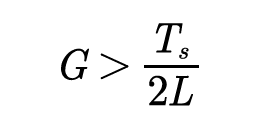
若PFC 在整个工频周期都工作于DCM 模式,需满足条件:
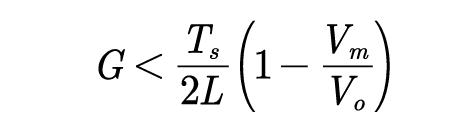
当输入导纳在两者之间时,CCM 模式与DCM 模式混合存在。
2.占空比前馈控制
2.1CCM 模式下理想占空比
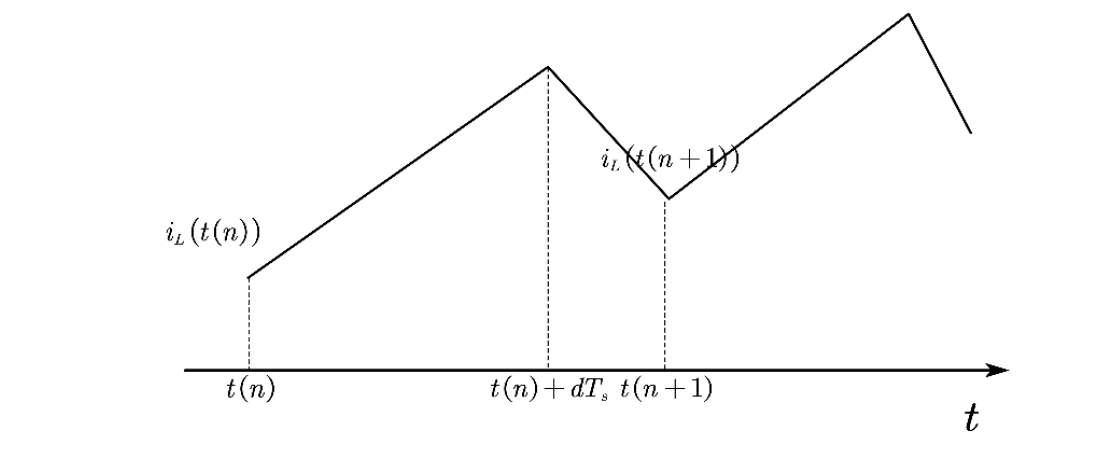
当PFC 工作于电流连续模式时,第n 个周期的电感电流示意图如上图所示。
占空比为d, iL(t(n))与 iL(t(n+1))分别是第n 个开关周期开始和第n 个周期结束
时的电感电流大小, iL(t(n)+dTs)为第n 个周期开关管关断时刻的电感电流大小。
当t(n)<t<t(n)+dTs时,开关管开通,此时有:
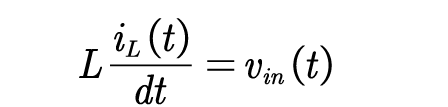
当t(n)+dTs)<t<t(n+1)时开关管关断:
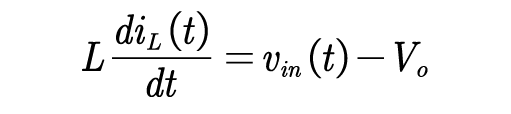
设输入电压为,
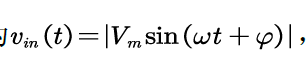
由平均开关模型:
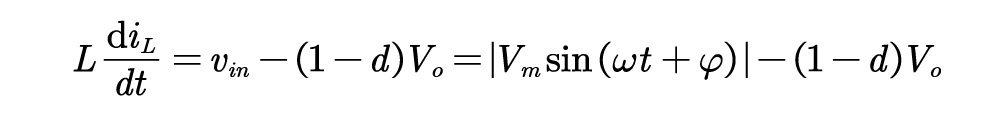
定义开关管关断占空比为:
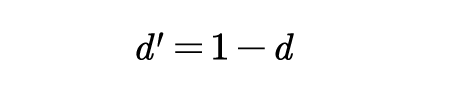
设交流输入电压为
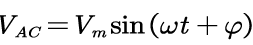
那么上式可以表达为:
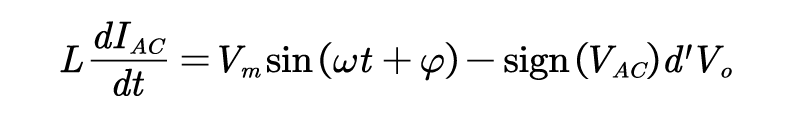
其中为符号函数,
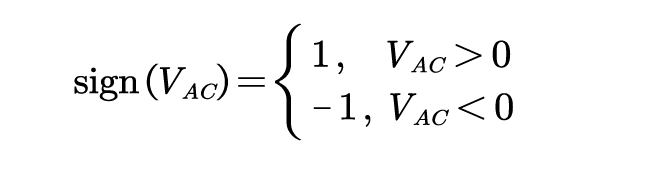
设功率因数为1,即从交流端看过去PFC 呈纯电阻性,设等效电阻大小为,则
有:
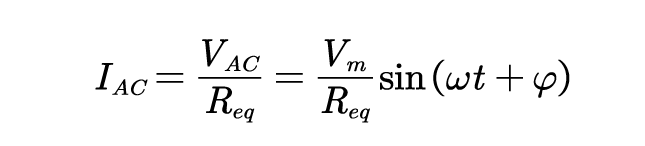
带入上式有:
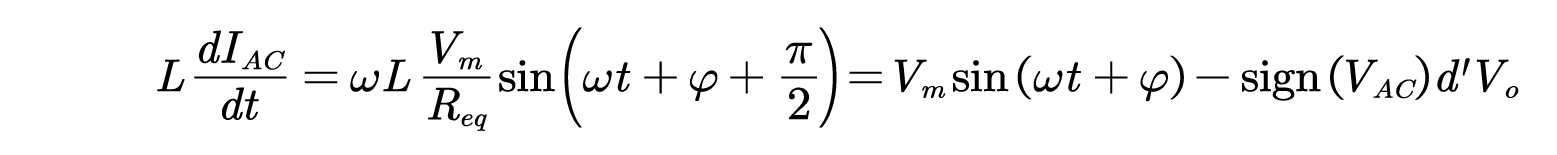
由上式得:
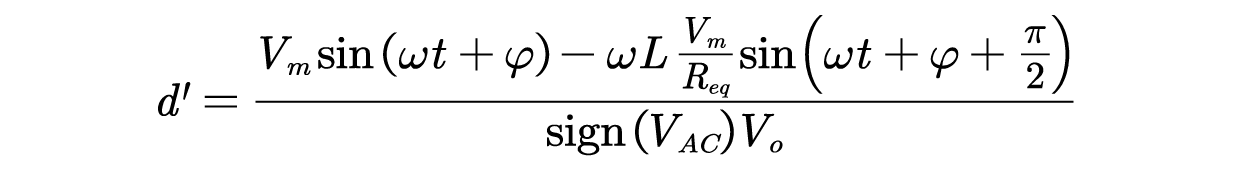
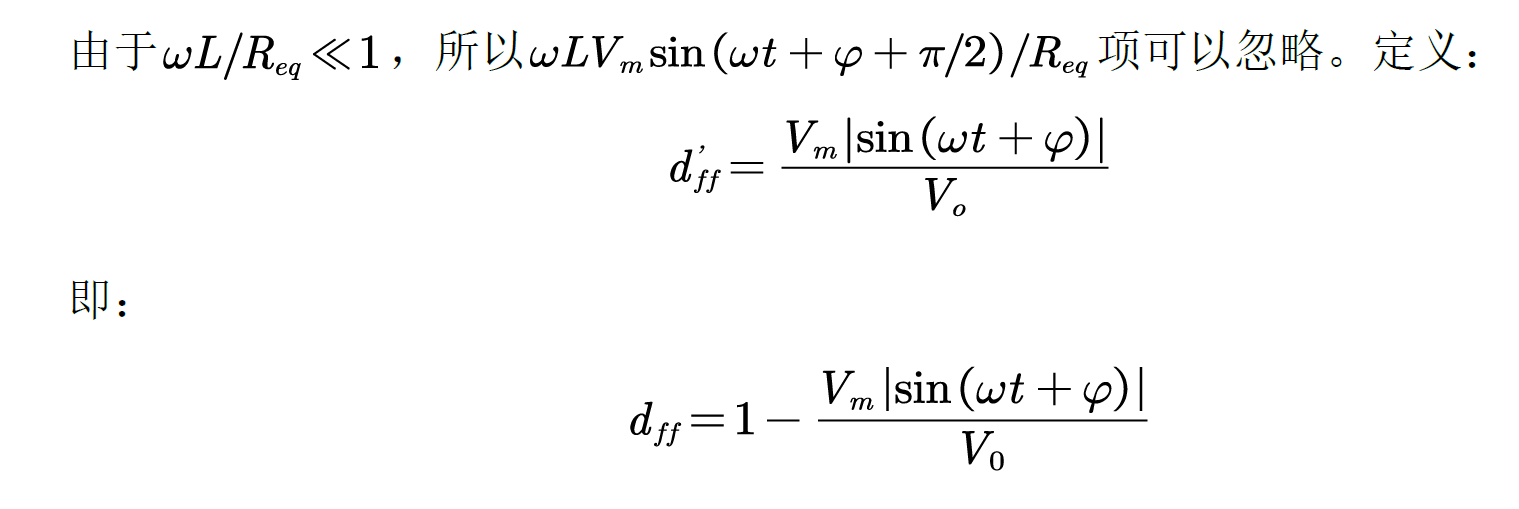
从上式可以看出电感电流稳定状态由输入电压和占空比共同决定,而输入电压可被视为是扰动,所以考虑将其加入到前馈环节可以抑制交流侧电压引起的扰动。
2.2DCM 模式下理想占空比
在一个开关周期内,电感电流峰值为:
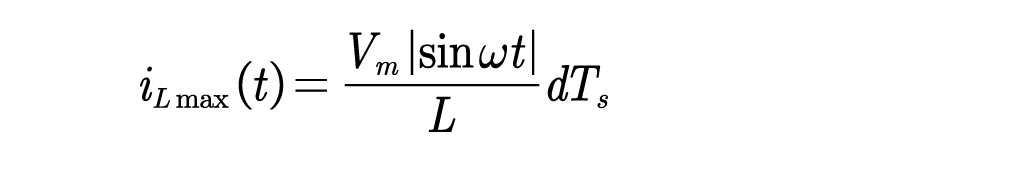
忽略直流侧电压波动,由伏秒平衡可得:
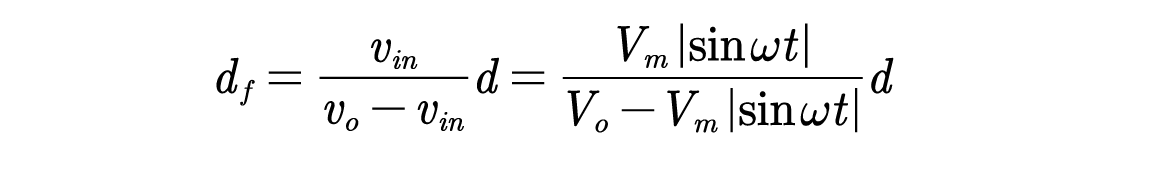
电感电流平均值为:
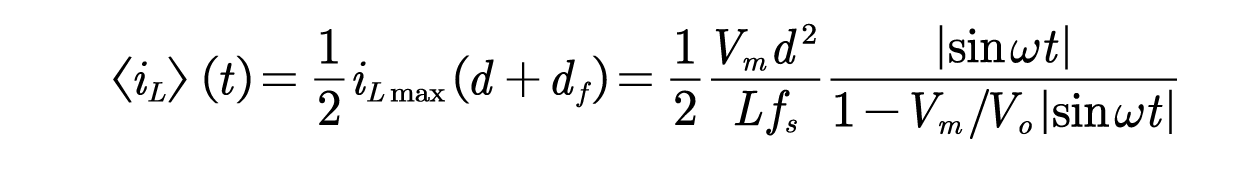
其中是开关频率,所以输入电流为:
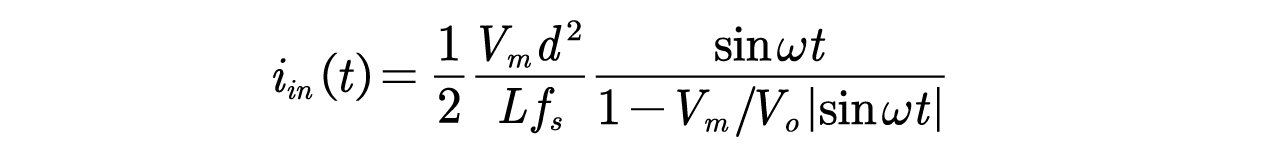
假设占空比固定,对输入电流进行标幺化,基准值:
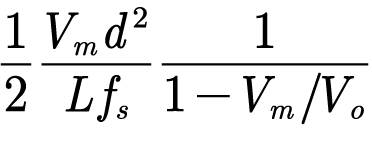
标幺化后的输入电流表达式为:

半个工频周期标幺化后输入电流理论值波形如下图所示:
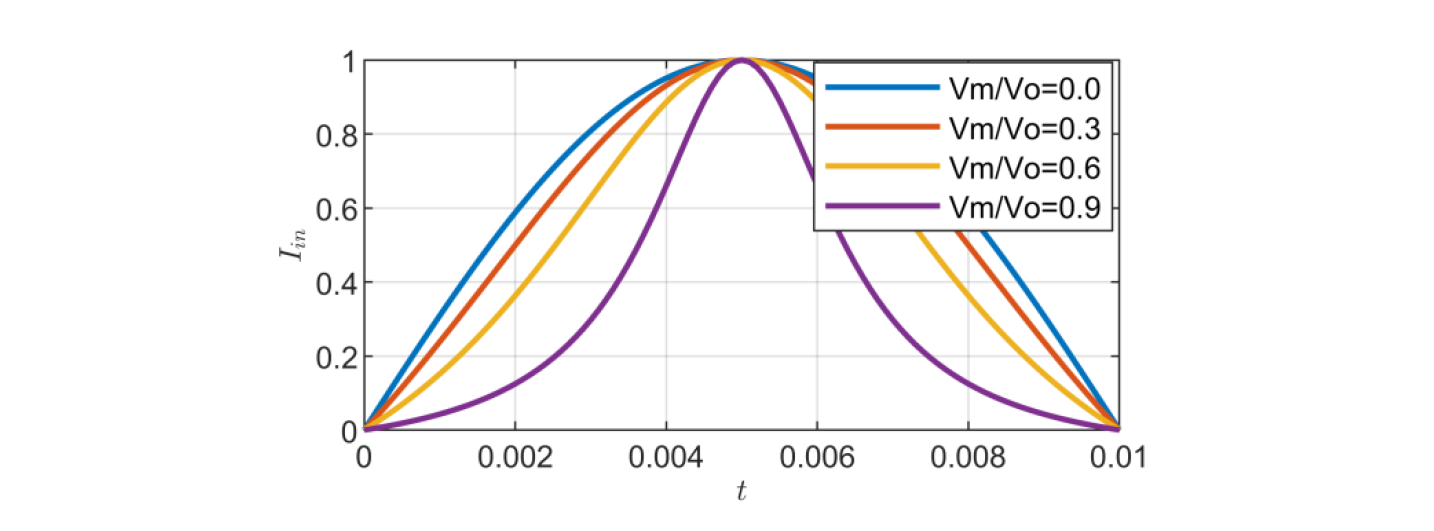
可以看到,当输出电压一定时,输入电压有效值越大,波形畸变越严重。为了使输入电流为正弦波形,取:
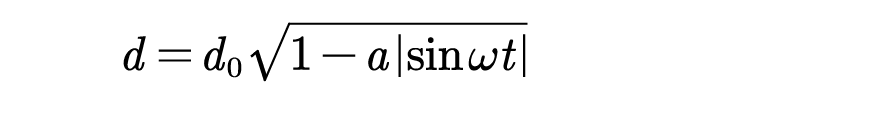

输入功率为
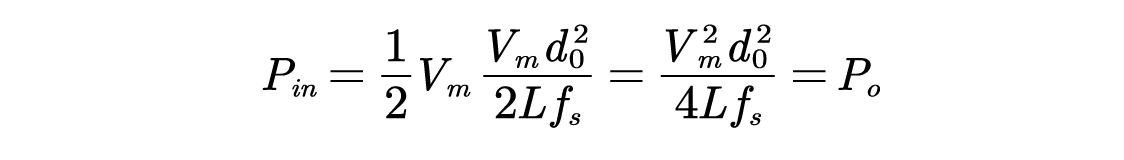
若要使输入电流为正弦波,即PF=1,可得
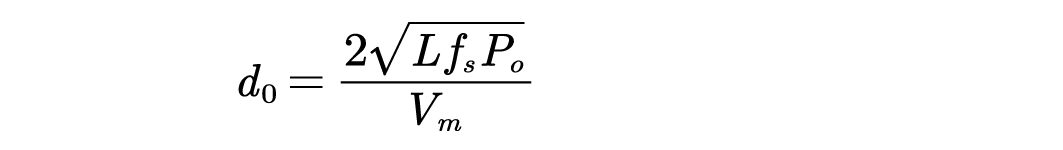
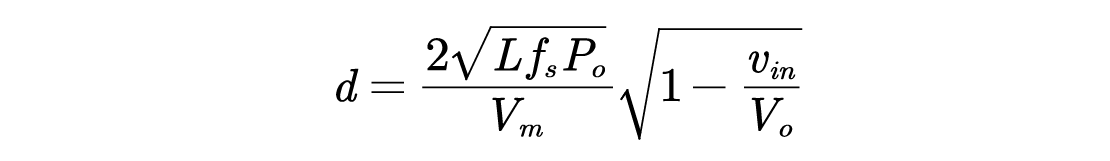
为了方便数字控制实现
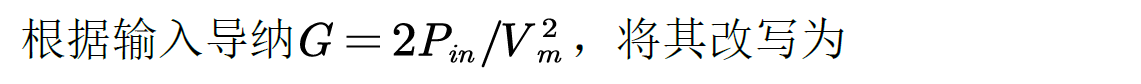
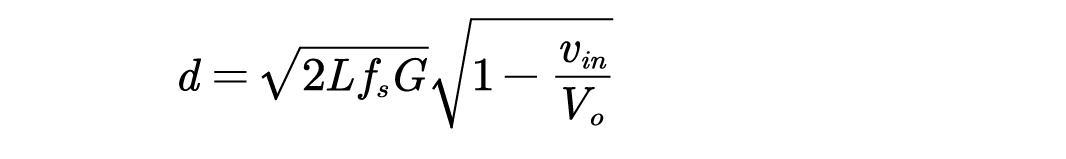
即DCM 模式下使得输入电流正弦较高期望占空比.
3.占空比前馈优化控制方案
绘制出不同功率下理想占空比曲线图:
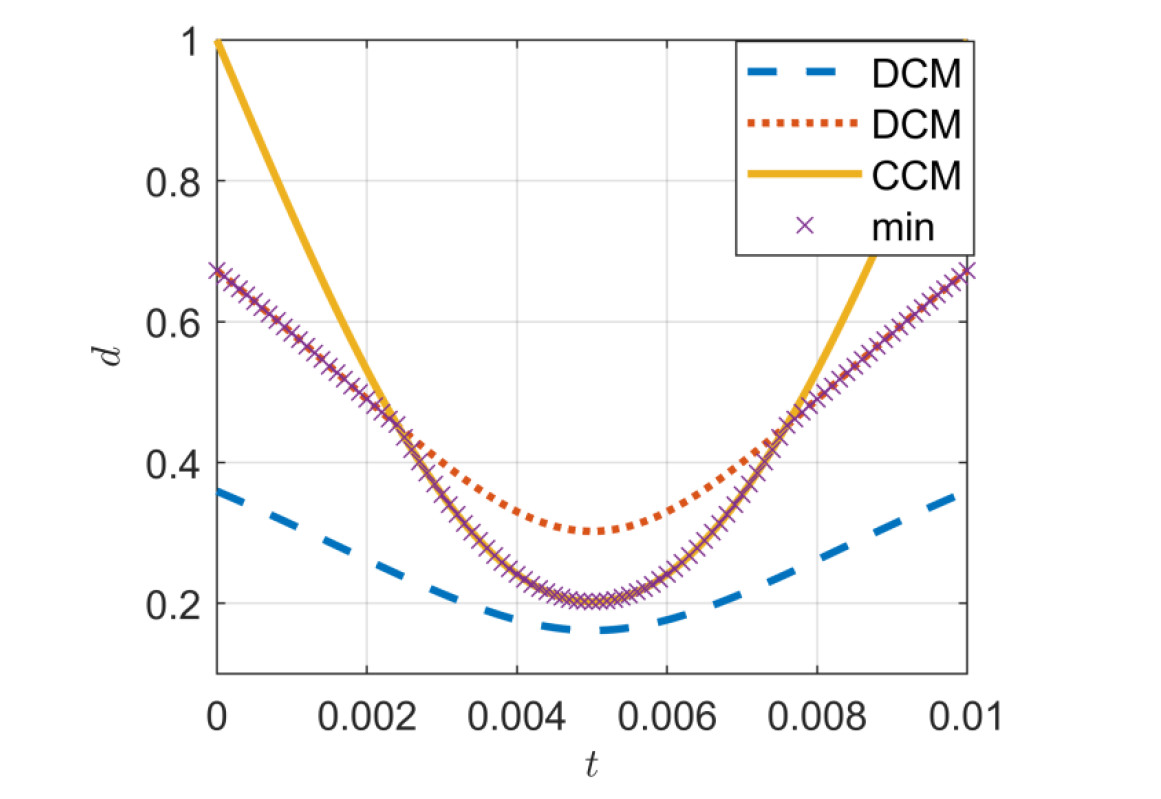
可知,当 DCM占空比曲线与 CCM占空比曲线相交时,为临界导通 点;在临界之间系统处于 点;在临界之间系统处于 CCM模式,临界点两端系统处于 模式,临界点两端系统处于 模式,临界点两端系统处于 DCM模式。所以在 模式。所以在 半个周期内, DCM理想占空比与 CCM理想占空比较小者即为,能使 输入电流正弦度提高,提高功率因数。
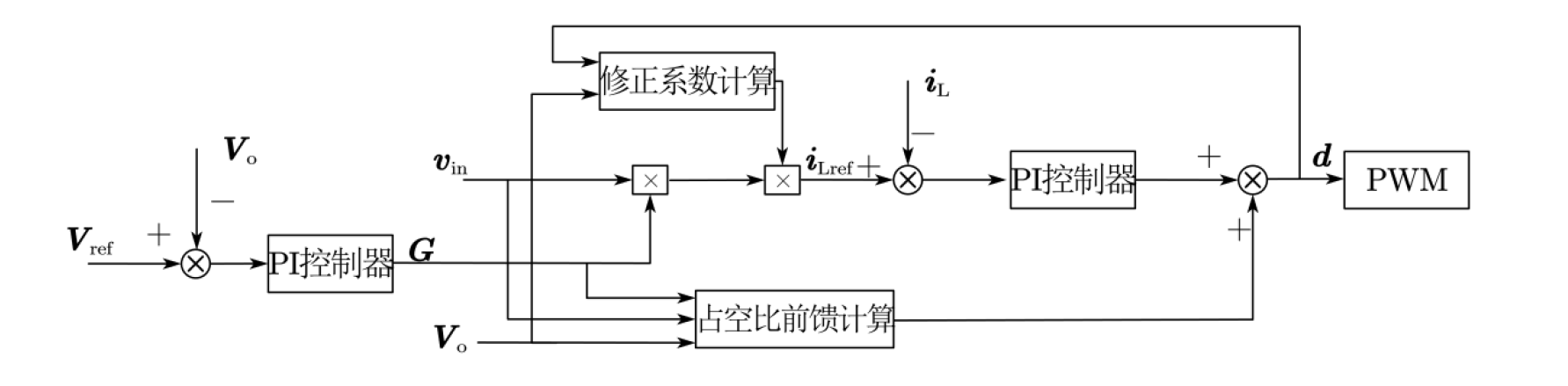
由以上讨论,考虑前馈 由以上讨论,考虑前馈 DCM模式理想占空比与 CCM模式理想占空比较小者, 即为 PFC系统有效占空比;得出改进后的控制框图 如系统有效占空比;得出改进后的控制框图 如系统有效占空比;得出改进后的控制框图 如上图所示 ,在平均电流控制 基础上加入变占空比前馈,并且引了第二章讨论的参考电流修正环节当 boost PFC系统处于 CCM模式 时,修正系数 等于 1,系统处于 DCM模式时,修正系数 模式时,修正系数 大于 1,使得平均电流 ,使得平均电流 正弦度提高 。占空比前馈与指令电流修正结合 占空比前馈与指令电流修正结合 ,可以使数字 控制 PFC系统 适应输出功率宽范围变化。 适应输出功率宽范围变化。
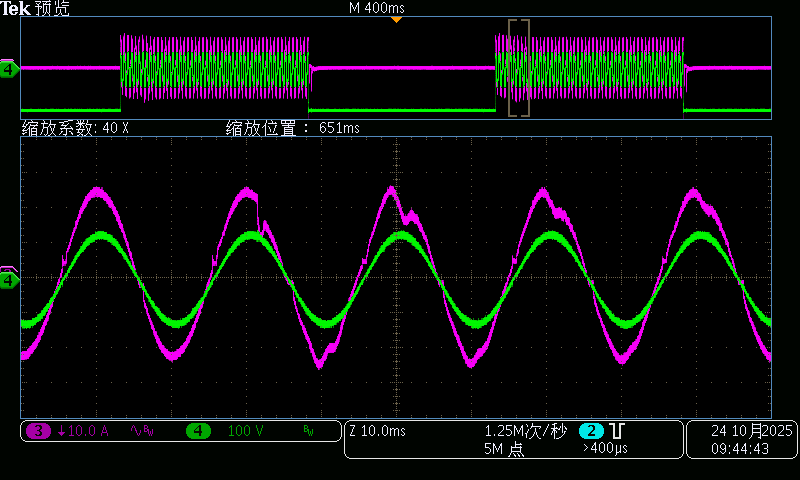
性能优化之AC DC切换的pfc波形如下图所示,后续有时间进行详细描述此优化算法的过程。
附录1
90V交流电压切320V直流电压 90度切换波形
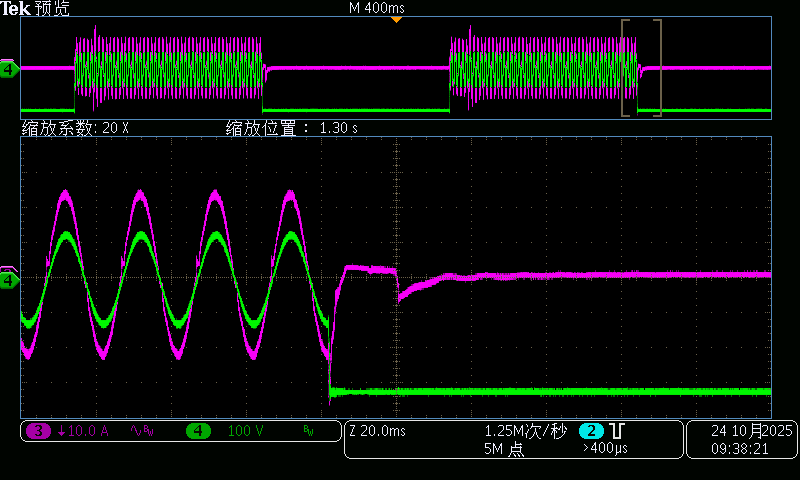
320V直流电压切90V交流电压 90度切换波形
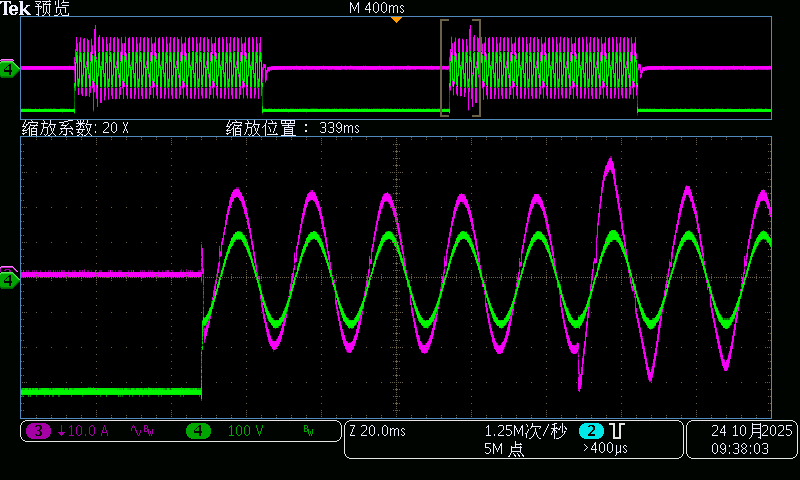
整体切换过度波形
附录2
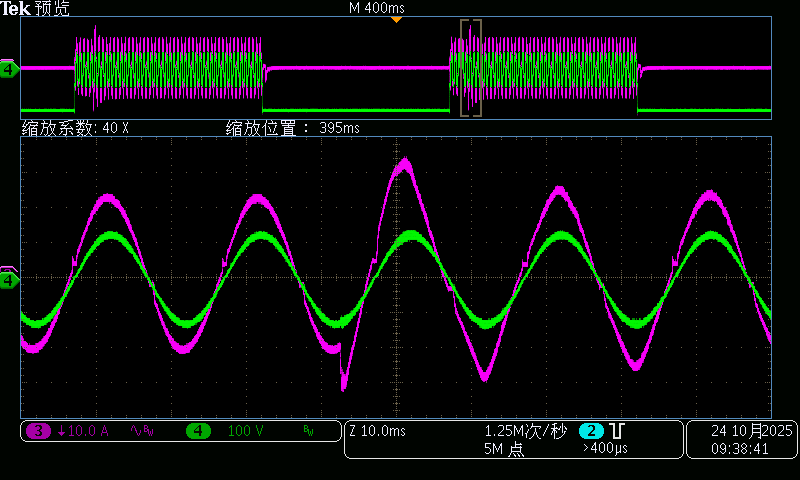
90V交流电压切320V直流电压 270度切换波形
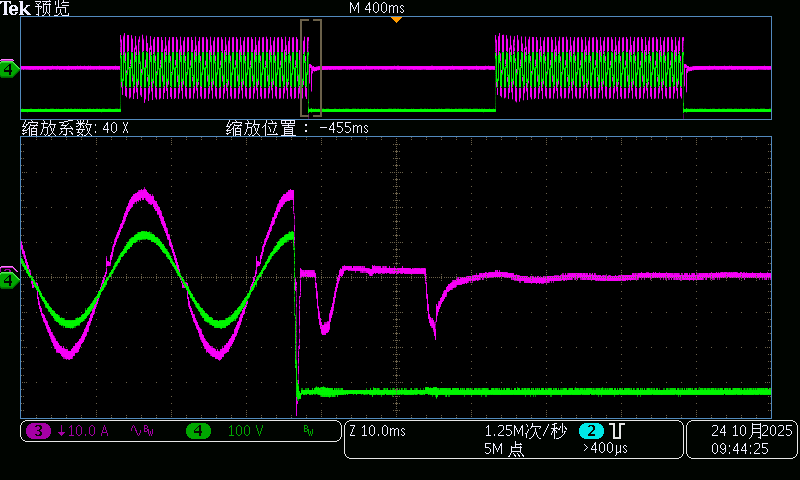
320V直流电压切90V交流电压 270度切换波形

整体切换过度波形