当前位置：首页 > news >正文

Diffusion-TS：一种基于季节性-趋势分解与重构引导的可解释时间序列扩散模型

news 2025/10/25 9:26:22

1 模型架构描述

Diffusion-TS的模型结构始于将时间序列数据输入一个基于Transformer的编码器进行编码，以获得其全局的向量表示。解码器随后对这些表示进行解码，其输出通过一个权重矩阵进行映射后分流：一部分送入趋势合成层，另一部分进入傅里叶合成层。输入全连接神经网络（FFN）的部分经处理后，对已经过自注意力机制和交叉注意力机制处理的时序特征进行非线性变换和维度提升，此举显著增强了模型从加噪输入中捕获复杂依赖关系的能力。处理后的特征再与解码器的中间输出向量进行逐元素相加，以整合信息。图1清晰地展示了这一解码器架构。

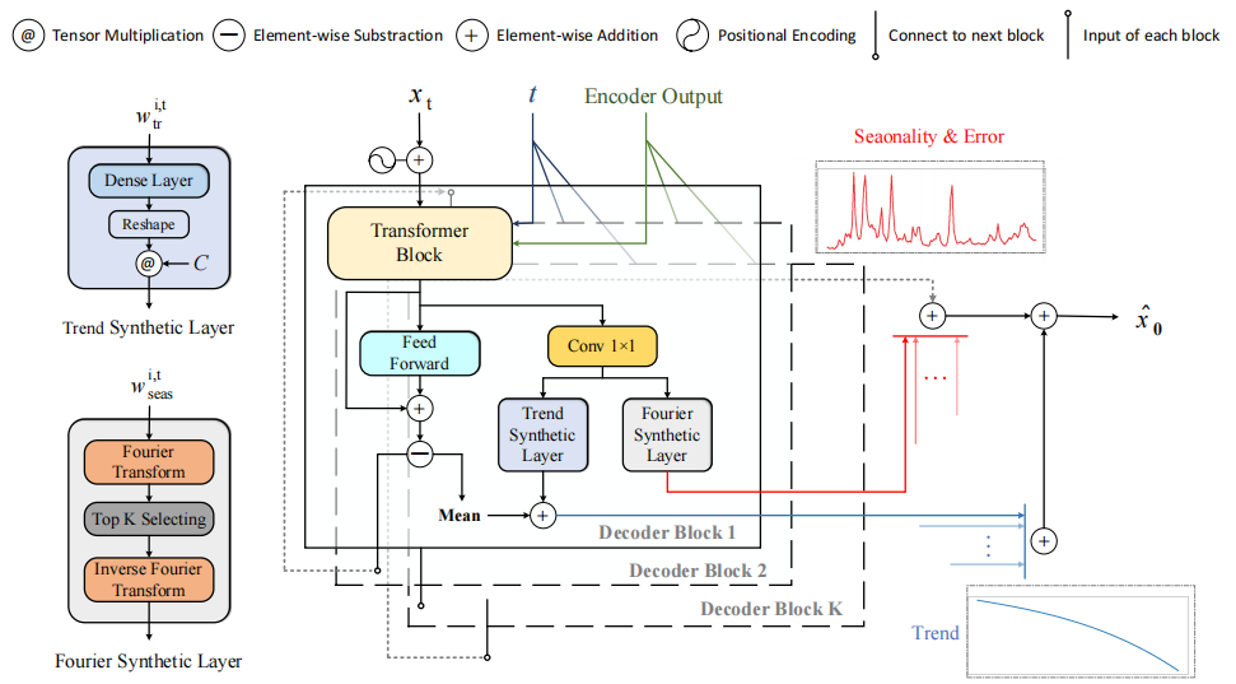
图1 Diffusion-TS的模型结构图

在趋势提取方面，模型通过让Transformer、FFN及加减运算协同工作，专注于学习一个相对简化的任务——预测序列的“基线”或“平均水平”。这个基线本质上是趋势成分最核心的体现，即模型对去除噪声和季节性波动后序列平滑基线的估计（表示为“Mean”）。具体而言，Transformer层产生中间特征表示 $W_{i,t}$ ，其中一部分用于计算均值 $X_{i,t}$ 。随后，模型使用多项式回归器来显式地建模趋势成分 $V_{tr}^{t}$ ，其公式如下：

$V_{t,r}^t = \mathcal{X}_{t,r}^t \cdot C$

其中，C是一个由向量 $C = \left\{ \mathbf{c} = [0, 1, 2, \ldots, \tau-1]^{T} / \tau \right\}$ 的幂次构成的矩阵（多项式空间），p是一个较小的阶数（例如3），用于模拟低频行为。这个设计旨在捕获平滑、缓慢变化的趋势。

随后， $W_{i,t}$ 减去该趋势成分得到一个去趋势的信号，此信号被传递给傅里叶合成层进一步提取季节性成分。该层基于傅里叶级数，通过选择频域中振幅最大的K个分量来建模季节性，其数学表达为：

$V_{se}^{t} = \sum_{k=1}^{K} A_{i,t}^{(k)} \cos\left(2\pi f_{k}j + \Phi_{i,t}^{(k)}\right)$

这里， $A_{i,t}^{(k)}$ 和 $\phi_{i,t}^{(k)}$ 分别是第k个频率分量的振幅和相位，通过离散傅里叶变换 F得到，fk是对应的傅里叶频率。最终，原始信号的估计 x^0由趋势、季节性和残差（由最后一个解码器块的输出 R表示）相加重构而成：

$\hat{x}_{0} = V_{tr}^{t} + V_{se}^{t} + R$

这种显式的、基于公式的分解是模型可解释性和高生成质量的关键来源。

2 扩散过程与条件生成机制

原始扩散模型的反向过程由 $p_{\theta}(x_{t-1} \mid x_{t}) = \mathcal{N}(x_{t-1}; \mu_{\theta}(x_{t}, t), \Sigma_{\theta}(x_{t}, t))$ 描述，其目标是从噪声 xT中通过去噪过程还原出原始数据 x0。这个过程本质上是无条件的，模型的核心是学习原始数据分布 p(x0)。Diffusion-TS的一个关键设计是修改了训练目标，它不直接预测噪声 ϵ，而是训练神经网络直接预测一个对原始样本的估计 $\hat{x}_{0}(x_t, t, \theta)$ ，并结合了一个傅里叶基损失（Fourier-based loss）项 $\mathcal{L}_{FFT} = \|FFT(x_{0}) - FFT(\hat{x}_{0})\|_{2}^{2}$ 来增强频域重建的准确性。最终的总损失函数为：

$\mathcal{L} = \lambda_{1}\|x_{0} - \hat{x}_{0}\|_{2}^{2} + \lambda_{2}\mathcal{L}_{FFT}$

这个设计迫使模型同时优化时域和频域特征。这一设计的关键优势在于，它解决了单一时域损失MSE在捕获复杂周期模式上的不足。MSE项保证生成序列在时间维度上的基本保真度，而FFT损失则专门确保其周期性行为的真实性。

原始扩散模型的反向过程由 $( p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))$ 描述，其目标是从噪声 $x_T$ 中还原原始数据 $x_0$ 。这个过程是无条件的，模型主要学习原始数据分布 $p(x_0)$ 。为了支持条件生成，Diffusion-TS引入了分类器引导机制。该方法通过后验概率分布 $p(x_{0:T} y) = \prod_{t=1}^{T} p(x_{t-1} x_t, y)$ 进行近似采样，并基于 $p(x_{t-1}\mid x_t, y) \propto p(x_{t-1}\mid x_t) \cdot p(y\mid x_{t-1}, x_t)$ 推导梯度计算过程，具体步骤如图2所示。

图2 分类器引导扩散模型的条件概率梯度推导

其核心改进是在原始扩散模型的反向传播中加入了外部条件y ，引导生成过程产生符合条件的时间序列。相应的对数概率梯度分解为：

$\nabla_{x_{t-1}} \log p(x_{t-1}\mid x_t, y) = \nabla_{x_{t-1}} \log p(x_{t-1}\mid x_t) + \nabla_{x_{t-1}} \log p(y\mid x_{t-1})$

其中，无条件扩散模型的先验概率确保生成数据符合真实分布，而分类器梯度则评估当前中间结果 $x_{t-1}$ 符合目标条件y的程度，并提供调整方向。该梯度信号通常由预训练的判别模型提供。

在插补和预测等具体任务中，条件采样方法表示为：

$\hat{x}_0(x_t, t, \theta) = \tilde{x}_0(x_t, t, \theta) + \eta \nabla_{x_t} \left\| x_a - \tilde{x}_a(x_t, t, \theta) \right\|_2^2 + \gamma \log p(x_{t-1} \mid x_t)$

这里， $\hat{x}_0(x_t, t, \theta)$ 是经梯度引导修正后的最终预测结果， $\tilde{x}_0(x_t, t, \theta)$ 是Diffusion-TS的无条件预测值。该方法在原始扩散模型的先验概率似然项基础上增加了重构损失项 $\left\| x_a - \tilde{x}_a(x_t, t, \theta) \right\|_2^2$ ，旨在使生成样本中与条件对应的部分 $x_a$ 尽可能接近真实值。先验概率作为正则项，防止生成过程为过度拟合条件而偏离真实数据分布，从而保持生成样本的多样性和真实性。梯度项引导 $x_t$ 变化，使得模型预测的 $\hat{x}_0$ 在条件部分 $x_a$ 上逼近真实值。这种设计极具灵活性：同一个预训练的Diffusion-TS模型只需在采样时更换引导函数（如从插值条件改为预测条件），即可适应不同下游任务，实现“即插即用”。

值得注意的是， $\tilde{x}_a(x_t, t, \theta) := \sqrt{\bar{\alpha}_t} x_a + \sqrt{1 - \bar{\alpha}_t} \epsilon$ 表示将真实条件 $x_a$ 通过前向扩散过程加噪至时间步t后的状态。在生成过程中，会将生成样本里对应已知条件 $x_a$ 的部分强制替换为该加噪真实值，以确保去噪过程中已知部分始终与真实条件严格匹配，增强条件生成的一致性。此后，利用新的 $\hat{x}_0$ 还原出 $x_{t-1}$ 。

3 采样算法与优化

扩散模型的反向过程可划分为早期“创造阶段”和后期“平滑阶段”。论文中提出了重构引导采样算法，如图3中的算法1所示。该算法从完全噪声 $X_T \sim \mathcal{N}(0, I)$ 开始迭代去噪。在每个时间步，它从原始预测的 $\hat{x}_0$ 中分割出对应原始条件数据 $x_a$ 的部分和需生成的部分 $x_b$ ，将两者拼接成完整序列后计算重构损失 $L_1$ 。接着执行一次无条件去噪，使用 $\hat{x}_0$ 和 $x_t$ 计算均值 $\mu$ ，并从构造的分布中采样出 $x_{t-1}$ 。随后计算模型先验损失 $L_2$ （即采样得到的 $x_{t-1}$ 与理论均值 $\mu$ 的差异）。关键的第7步对应上述梯度引导更新公式，第8步则执行引导后的去噪过程，重新计算均值并采样得到新的 $x_{t-1}$ 。 $Replace(x_a, x_{t-1}, t)$ 操作将新采样的 $x_{t-1}$ 中对应已知条件 $x_a$ 的部分，用真实条件数据加上时间步t-1的对应噪声替换，以确保条件一致性。

图3 重构采样算法伪代码

算法2是算法1的优化版本，其核心改进是引入了动态调整的梯度更新次数K[t]，该参数表示在扩散时间步t重复执行梯度更新的次数。在噪声较多的早期创造阶段，设置较大的K[t]值，通过多次梯度更新强条件引导，确保生成样本的基础结构与给定条件高度一致。在噪声较少、数据已较清晰的后期平滑阶段，则设置较小的K[t]值，减少不必要的计算开销，加速采样过程，因此阶段过度优化收益已不显著。

4 核心收获与创新启发

通过研读Diffusion-TS的相关文献，我在改进基础条件生成模型方面获得了一些收获以及创新思路。

主要收获如下：

1. 可解释性驱动的架构设计：Diffusion-TS将季节性-趋势分解技术融入扩散模型的去噪网络是一大创新。通过编码器-解码器架构中的趋势合成层与傅里叶合成层，模型能显式学习时间序列的趋势、周期项和残差等成分。这不仅提升了生成质量，其可解释的生成结果（可分解为具体时间模式）还为条件生成提供了语义层面的控制基础。

2. 基于重构的训练目标：与传统扩散模型预测噪声不同，Diffusion-TS直接预测原始样本 $\hat{x}_0$ 并结合傅里叶域损失。此设计迫使模型在去噪中同步优化时域和频域特征，尤其适合强周期性的时间序列数据，使条件生成能更精准地保持序列的频谱特性。

3. 灵活的条件控制机制：其提出的基于重构指导的采样算法，利用预训练扩散模型的条件得分估计，通过梯度更新引导生成样本满足约束（如已知片段），无需修改模型即可适配插值、预测等任务。这种“即插即用”的方式避免了传统方法需重新训练的问题。

由此衍生的创新思路包括：

1. 分层条件控制：可借鉴其分解架构，在条件生成时对趋势项和季节项分别施加不同约束。例如预测任务中，可用外部变量指导趋势生成，同时通过周期模板约束季节项，实现更细粒度的控制。

2. 动态权重机制：文献中的冷启动实验表明模型在数据缺失时仍稳定。由此可延伸出自适应权重策略——根据条件信息的完整度动态调整傅里叶损失与重构损失的权重。条件信息少时，增大频域约束权重以利用周期先验；条件信息充足时，则侧重时域重构精度。

3. 多尺度条件融合：参考其编码器提取全局特征的能力，可在条件生成时设计多尺度条件注入机制。例如，局部条件（如近期历史值）通过交叉注意力注入解码器，而全局条件（如整体统计量）作为扩散步长的嵌入向量，从而增强对长短周期条件的协同利用能力。

查看全文

http://www.dtcms.com/a/524619.html