光伏发电建模与性能分析:从半导体物理到输出功率预测
摘要:光伏发电模型主要采用等效电路模型,包括单二极管三参数、四参数、五参数及双二极管七参数模型,其中单二极管五参数模型应用最广泛。模型参数可通过解析法、I-V曲线拟合法及智能算法确定。单二极管模型通过引入串联电阻Rs和并联电阻Rp提高精度,而双二极管模型能更好反映耗尽区复合损耗。光伏电池输出功率受温度显著影响,温度升高会降低开路电压和填充因子。效率与温度呈线性关系,常用表达式包含温度系数。实际应用中需考虑工作温度与环境因素,通过标准测试条件与现场偏差建模预测性能。典型硅基光伏组件在25℃参考温度下平均效率为12%,温度系数约0.0045/℃。
1 光伏发电模型
太阳电池的数学模型中最常用的是等效电路模型。依据未知参量个数的不同,等效电路模型包括单二极管三参数模型、单二极管四参数模型、单二极管五参数模型和双二极管七参数模型等,其中以单二极管五参数模型的应用最广泛。模型参数的确定方法有利用出厂参数的解析法、I-V曲线拟合法和软件计算法(如遗传算法、差分进化、粒子群优化等)。
基于等效电路的模型被广泛用于模拟PV电池。使用电路模型的主要优点是MATLAB和PSpice等标准电气软件的可用性。PV电路模型可以无缝的集成到更大的PV系统中,包括电源转换器,电网连接等。
我们首先假设在照明下有一个均匀的半导体。如果p0和n0为热力学平衡载流子浓度,由给体或受体掺杂浓度决定,则电子浓度dn和空穴浓度dp的变化可表示为:
![]()
非简并半导体的载流子浓度由式给出
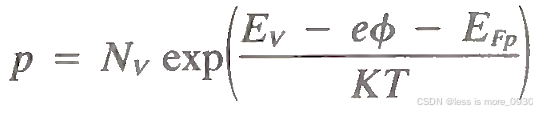
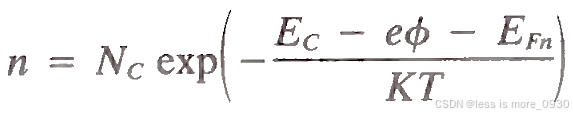
其中电势f与局部电场的关系式为E = -gradf。Nc和Nv分别为导带和价带的态密度(能量介于E~E+∆E之间的量子态数目∆Z与能量差∆E之比),EFn和EFp分别为电子和空穴的准费米能,n和p分别为它们的浓度,e为(正)电子电荷。
描述半导体中电子和空穴在光照下的通量的基本方程是电流密度方程(载流子浓度为标量,求梯度(grad)后为矢量:
![]()
和连续性方程(电流密度方程为矢量,求散度(div)后为标量):
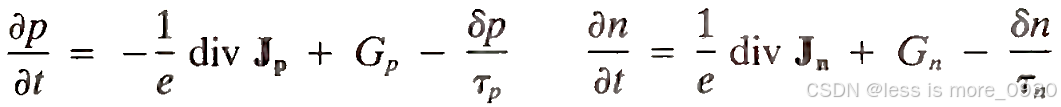
扩散系数Dn和Dp与载流子的迁移率μn,μp有关,根据一般的爱因斯坦关系D = (kT/e)w。对于光生成的载流子,电子和空穴的生成速率等于Gn=Gp=G。如果过量浓度较低,则可以另外假设dn = dp,并将(2.13)和式(2.12)结合起来。例如,对于孔洞,我们得到:
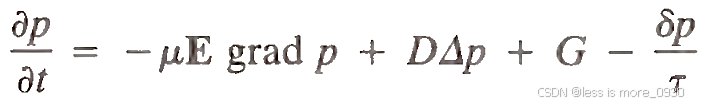
其中双极性扩散系数D和双极性迁移率μ为:
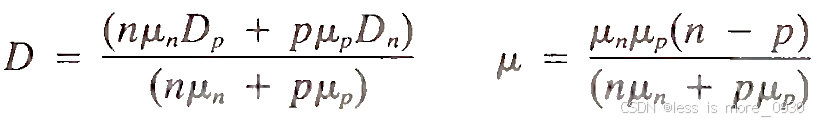
在进行光伏电池的建模之前,需要了解光伏电池的基本结构及其与入射光的关系。光伏能量转换需要通过内部电场将电子和空穴分离,典型硅光伏电池的简化结构如图1所示。为了减少入射辐照的阻碍,电极的上侧采用薄而不连续的结构,手指状的金属元件嵌入到硅中。它的大小和形状的设计,以最大限度地吸收表面光照和减少接触阻力。
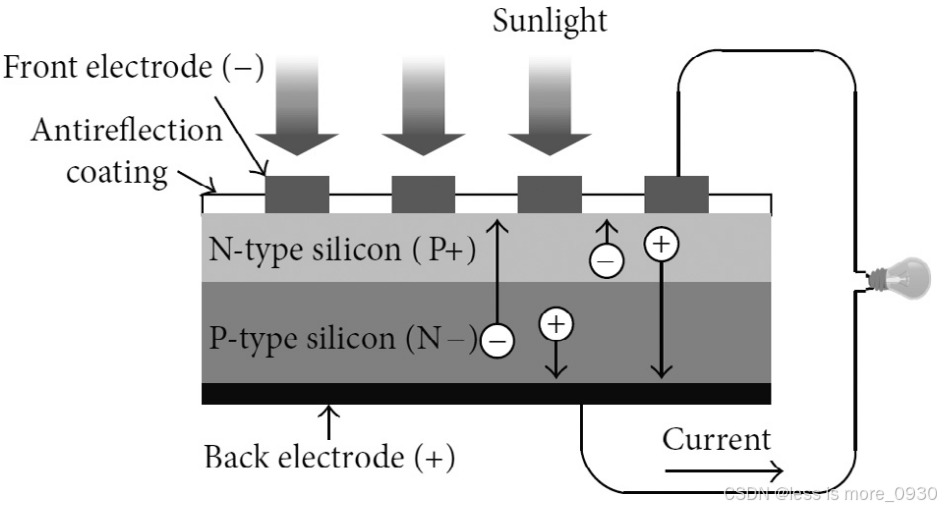
图1 光伏二极管结构图
太阳能电池需要特殊的pn结设计,如图1所示。它由靠近前表面形成的浅结(shallow junction在光伏电池中,浅表结的设计可以优化光生载流子的收集效率,减少载流子在结区的复合损失,从而提高光伏电池的转换效率。此外,浅表结还有助于降低光伏电池的表面反射率,增加光线的吸收。)、条状和指状形式的前接触电阻以及覆盖整个后表面的后接触电阻组成。在大多数情况下,pn结太阳能电池被当作一维器件来处理,但为了真实地计算电流-电压特性,必须考虑特定器件的几何形状。内部电场E=-gradf使电子和空穴分布不均匀,计算电流需要解出完整的电流密度方程和连续性方程。对太阳能电池内部工作机理进行分析和计算,可得不同等效方式下的等效电路和I-V特性。
在没有太阳光照射的情况下,电池表现为一个简单的pn结二极管。它的特性由著名的肖特基二极管方程决定,该方程将二极管电流表示为:
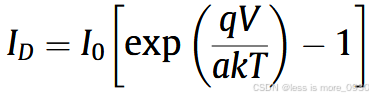
式中,I0表示饱和电流;常数q是电子电荷的绝对值(1.60217646*1019 C);V为二极管端电压;a是二极管的理想(或质量)因数;k为玻尔兹曼常数(1.380653*1023 J/K);T为pn结的温度(K);比值kT/q称为热电压(Vt)。
二极管的理想因子取值通常在1到2之间:
理想情况:当理想因子a=1时,表明二极管(如肖特基二极管)的势垒区无任何缺陷,器件的电流全来自于漂移电流,此时二极管的性能最好。对于PN结二极管来说,如果P区和N区的扩散电流起到支配作用,那么此时二极管的理想因子a=1。
非理想情况:当理想因子a=2时,表明二极管(如肖特基二极管)的势垒区存在大量的缺陷,导致器件的电流主要来源于缺陷复合电流。对于PN结二极管来说,如果PN结空间电荷耗尽区的复合电流起支配作用,那么理想因子a=2。
二极管的理想因子,也称为肖特基二极管的灵敏度(特指肖特基二极管时),是衡量所制备的二极管与理想状态下的二极管差异程度的参数。它反映了二极管的电流变化情况,具体取值会直接影响到系统中的参数值。二极管的理想因子主要受到半导体材料及其制造技术的影响。对于实际的光伏系统,二极管的理想因子还可能受到温度、光照强度、材料性质等多种因素的影响。通过衡量理想因子a的大小,可以判断二极管势垒区电流的主要来源,从而评估二极管的性能。例如,在光伏系统中,理想因子越高,表示二极管的性能越好,光伏系统的效率也就越高。
玻尔兹曼常数(Boltzmann constant)是物理学中的一个基本常数,用于描述热力学系统中微观粒子(如原子或分子)的平均动能与绝对温度之间的关系。
1.1 理想单二极管模型
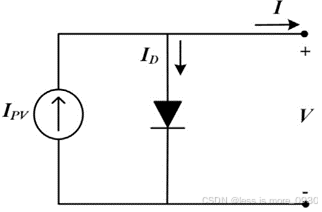
图2 理想单二极管光伏电池模型
由于辐照的存在,pn结吸收入射光中的光子并产生电子-空穴对(或载流子),在pn结处建立起电位差,电荷载流子开始在外部电路中流动。这种现象被称为光伏效应,由此产生的电流被称为光电流IPV。IPV的大小取决于入射辐照的通量以及半导体材料的吸收能力。将IPV包含到肖特基方程中,形成了对由并联到pn结二极管的电流源组成的照明单元的基本描述。这是理想光伏电池模型,如图2所示。电池的输出电流等于光电流减去二极管电流,表达式为:
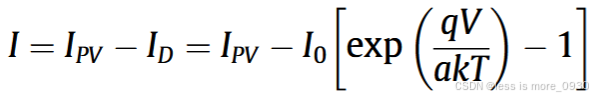
式中,I为光伏电池输出电流;IPV为光伏电池产生的总电流;ID为二极管电流;I0表示饱和电流;常数q是电子电荷的绝对值(1.60217646*1019 C);V为二极管端电压;a是二极管的理想(或质量)因数;k为玻尔兹曼常数(1.380653*1023 J/K);T为pn结的温度(K)。
由上式可知,该模型需要三个参数,即光电流(IPV)、饱和电流(I0)和理想因数(a)来充分表征I-V特性曲线。还可以注意到,I是IPV和ID的叠加,如图3所示。IPV决定了曲线的垂直平移,而ID定义了曲线的指数形状。
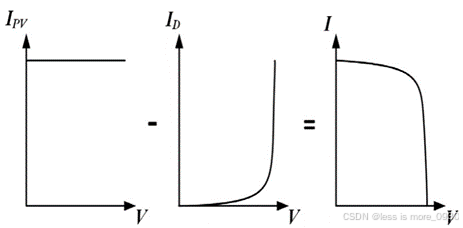
图3IPV和ID的叠加
1.2 单二极管Rs模型
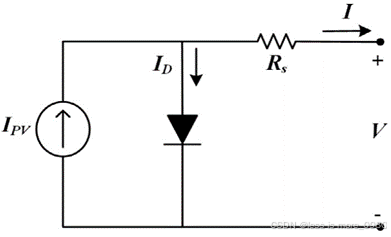
图4 单二极管Rs光伏电池模型
理想的单二极管模型很少被用作光伏模拟器的工作模型,它只是用来解释电池建模的理论概念。为了切合实际,硅和电极表面之间的接触电阻、硅材料中的电流流动电阻和电极的电阻所造成的损耗均需要考虑。表示这些损耗的一种方法是在理想模型中加入一个串联电阻(Rs)。该模型被称为单二极管Rs模型,如图4所示。该模型需要确定IPV、I0、a、Rs四个参数值,参数之间的关系可以表示为:
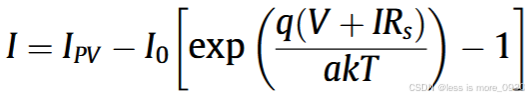
式中,I为光伏电池输出电流;IPV为光伏电池产生的总电流;I0表示饱和电流;常数q是电子电荷的绝对值(1.60217646*1019 C);V为二极管端电压;Rs为串联电阻;a是二极管的理想(或质量)因数;k为玻尔兹曼常数(1.380653*1023 J/K);T为pn结的温度(K)。
1.3 单二极管Rp模型
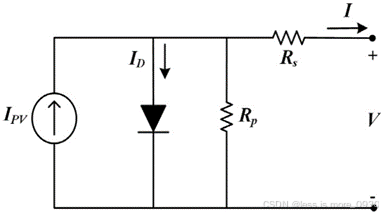
图5 单二极管Rp光伏电池模型
虽然Rs模型比较简单,但当电池经历较大的温度变化时,其精度会有所下降。这是因为该模型确实需要考虑电压VOC和温度系数(Kv)的作用。通过加入分流电阻Rp,可以提高温度灵敏度,如图5所示,该模型被称为单二极管Rp模型。另外,Rp的存在对应于pn结的泄漏电流。制造方法的不同,会导致Rp的大小不同。加入电阻Rp后,输出电流表达式为:
![]()
Rp的加入使模型参数增加到5个,分别是IPV、I0、a、Rs和Rp。虽然引入电阻Rp提高了模型性能,但在低辐照度下模型的精度会下降,特别是在VOC附近。尽管如此,因为在简便性和精确性之间取得了很好的折衷,Rp模型为目前最主流的模型。使用该模型绘制的典型I-V和P-V曲线分别如图6(a)和(b)所示。
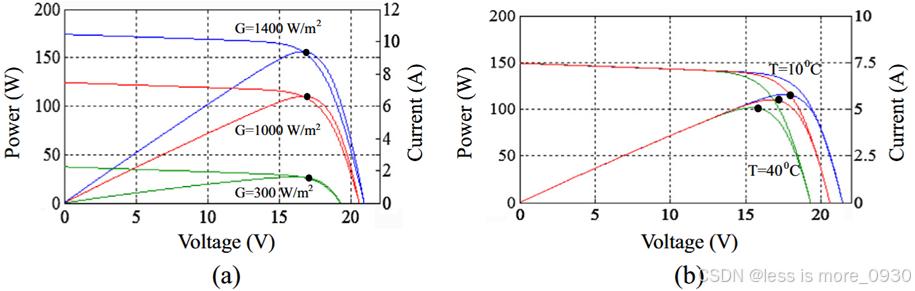
图6 典型的I-V和P-V曲线(a)变太阳辐照度和(b)变温度
1.4 双二极管模型
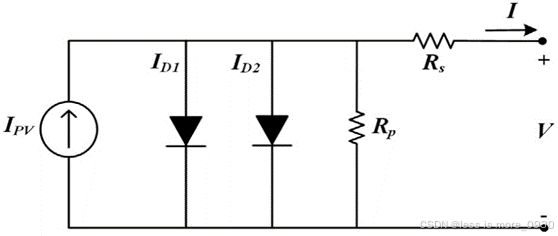
图7 双二极管光伏电池模型
迄今为止所讨论的单二极管模型都忽略了耗尽区复合电流损耗的影响。考虑到这种损耗,特别是在低电压情况下,因此提出了一种更精确的等效方法,称为双二极管模型。模型如图7所示。其输出电流表达式为:
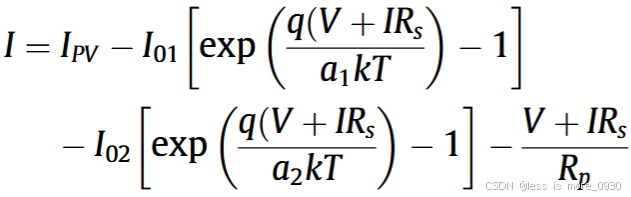
显然,需要考虑如何权衡饱和电流(I02)和第二个二极管的理想因子(a2)这两个新参数。这是在现有的IPV、I01、a1、Rs和Rp 5个参数的基础上增加到7个参数。此外,两个指数项使得保持合理的模拟时间存在巨大的挑战。然而,由于其在低辐照度条件下的优越精度,双二极管模型仍然是一个有吸引力的选择。
2 光伏电池的输出功率
2.1 伏电池的效率
温度对光伏电池/组件电效率的影响可以追溯到温度对电流I和电压V的影响,因为最大功率表达式为:
![]()
其中,Pm为最大输出功率;Vm为最大输出功率点电压;Im为最大输出功率点电流;FF为填充因子;Voc为开环电压;Isc为短路电流。
研究结果表明,开路电压和填充系数都随着温度的升高而大幅降低(因为热激发的电子开始主导半导体的电学特性),而短路电流只是轻微增加。因此,可得与温度成线性关系的电效率表达式:
![]()
式中,hTref和bref通常由光伏电池/模块制造商给出,hTref为参考温度和参考辐照度(1000 W/m2)下的电池/模块电效率;Tc为电池工作温度;Tref为参考温度;bref为温度系数,其计算公式为:
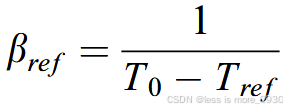
式中,T0为光伏组件的电效率降至零时的温度,对于晶体硅太阳能电池来说,这个温度为270°C。
在许多相关的电效率表达式中,由于电池/模块温度不易获得,故用标称工作电池温度TNOCT进行取代。
电池/模块的工作温度可通过标称温度由下式得到:
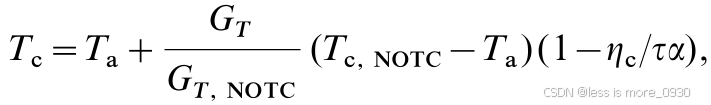
式中,Tc为电池工作温度;Ta为环境温度;GT为组件平面上的太阳辐照度;GT,NOTC为额定工作温度下组件平面上的太阳辐照度;Tc,NOTC为额定工作温度;t为电池盖透光率;a为电池对透射太阳辐射的吸收。
存在的一个事实是(hc/ta)<<1,因此可得简化后的表达式为:
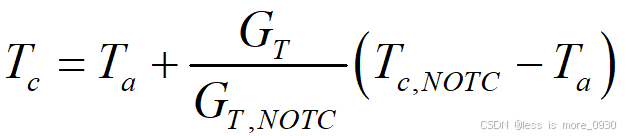
将用标称温度表示的光伏电池/模块的工作温度代入与温度成线性关系的电效率表达式,可得:
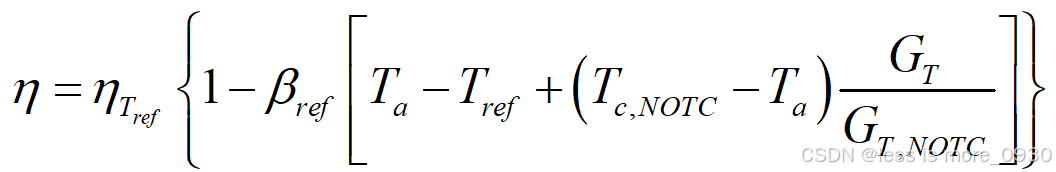
式中,hTref为参考温度和参考辐照度(1000 W/m2)下的电池/模块电效率;bref为温度系数;Ta为环境温度;Tref为参考温度;Tc,NOTC为额定工作温度;GT为组件平面上的太阳辐照度;GT,NOTC为额定工作温度下组件平面上的太阳辐照度。
除了光伏发电效率的“瞬时”值外,还可以写出月平均效率hc 的表达式。例如,一个光伏阵列的月发电量可根据下式估算:
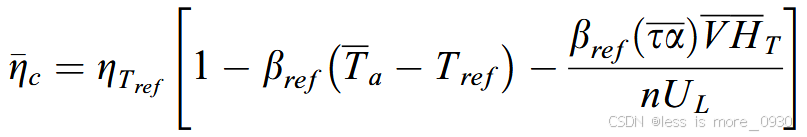
其中,上划线为月平均量,n为每天小时数,UL为总热损失系数,HT 为阵列平面上的月平均日照量,V 为日落角度、月平均清晰度指数、阵列月总辐射与水平表面辐射之比等量的无量纲函数。
汇总文献中的光伏电池/组件效率的一些方程如表1和表2所示。第一个表包含许多与温度成线性关系的电效率表达式的参数值,第二个表提供了hc的附加形式,包括每个相关性的相关注释。
表1 hT表达式参数汇总
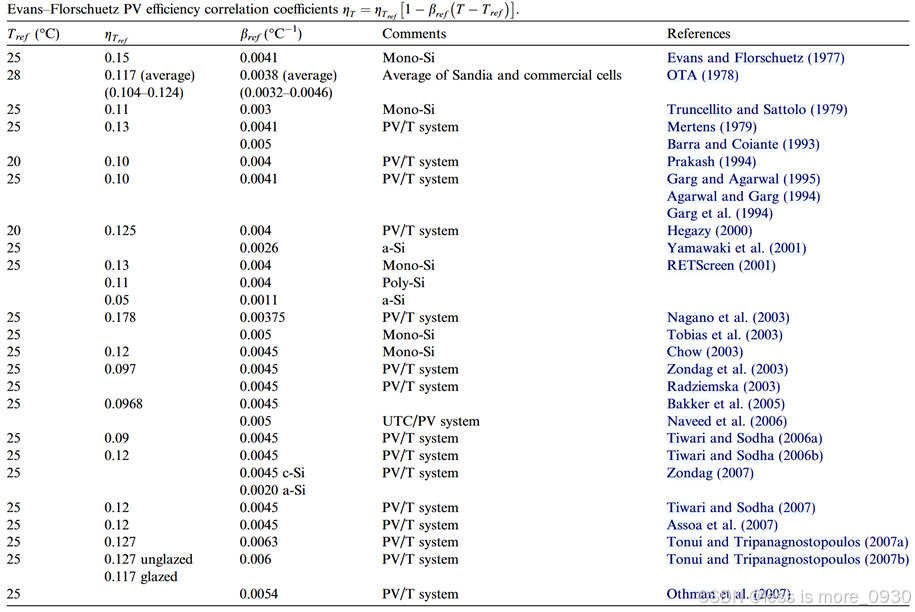
表2 光伏阵列关于温度的效率方程

根据表1所列数据,Tref = 25°C,平均href为0.12,平均bref为0.0045°C -1。温度系数对各种硅基光伏组件效率的影响如图8所示,其中Evans-Floschuetz比值hT/hTref是根据工作温度绘制的。
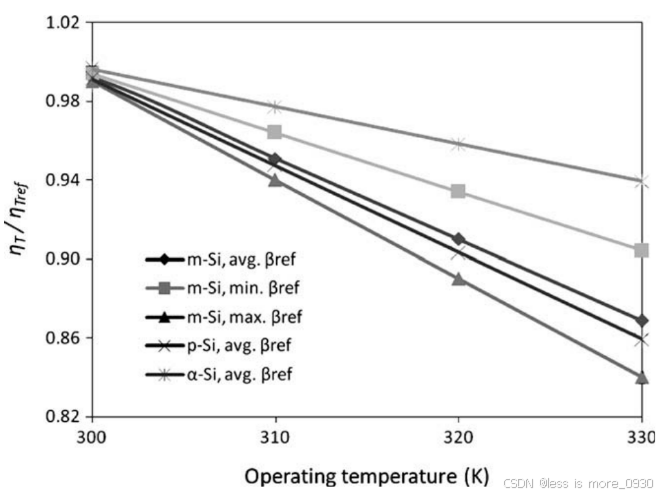
图8 根据Evans-Florschuetz效率相关性预测的典型硅基光伏组件类型的比值hT/hTref
2.2 光伏电池的功率
根据光伏组件在现场的输出功率预测其性能,即与组件制造商报告的标准测试条件的偏差,以类似于上述的方式建模。光伏电池/组件输出功率的表达式为:
![]()
P为电功率;hc为电功率效率;A为光伏组件孔径表面积;GT为组件平面上的辐照度。
表3 光伏阵列关于温度的输出功率方程

表3列出了文献中发现的光伏发电功率与电池/组件工作温度和基本环境变量之间的一些相关性。其中许多是线性的,而另一些则更为复杂,例如一些非线性多变量回归方程。
光伏发电系统的输出功率可表示为:
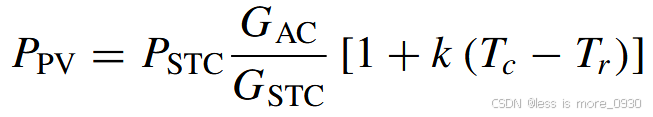
其中,温度系数k取值为0.0047/℃,参考温度Tr为25℃。
