算法练习：前缀和专题

前缀和是一种预处理技术，它能让我们在 $O(1)$ 的时间内（即常数时间）快速查询一个数组或矩阵某个区域内所有元素的和。

---

一维与二维前缀和(模板)

一、一维前缀和

第一个代码解决的是“一维数组区间和”问题。

1. 核心思想

我们定义一个“前缀和数组” dp (或称为 S)。
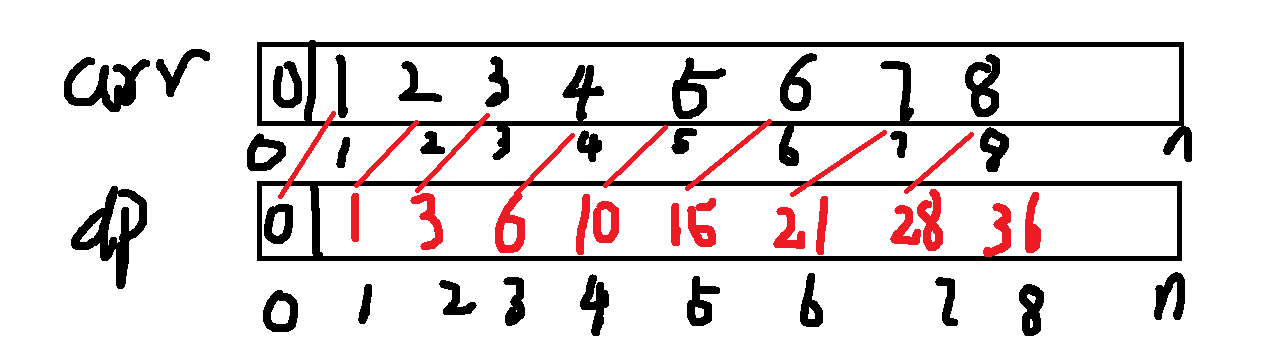
$dp[i]$ 存储的是原数组 arr 中从第 1 个元素到第 $i$ 个元素的总和。
即：$dp[i]=arr[1]+arr[2]+...+arr[i]$

2. 如何构建前缀和数组 (预处理)

根据定义，我们可以推导出递推公式：
$dp[i]=(arr[1]+...+arr[i-1])+arr[i]=dp[i-1]+arr[i]$

为了方便处理边界（例如查询从索引 1 开始的区间），我们通常让 $dp[0]=0$。

对应代码：

//2.预处理一个前缀和数组
vector<long long> dp(n+1,0);
for(int i = 1; i <= n; i++)
{// dp[i] 等于 前 i-1 项的和 (dp[i-1]) 加上当前第 i 项 (arr[i])dp[i] = dp[i - 1] + arr[i];
}

3. 如何使用前缀和数组 (查询)

如果我们想求原数组 v 中从索引 $l$ 到 $r$ 的区间和，即 $arr[l]+arr[l+1]+...+arr[r]$。

我们可以用 “前 $r$ 项的和” 减去 “前 $l-1$ 项的和” 来得到：
$(arr[1]+...+arr[r])-(arr[1]+...+arr[l-1])=dp[r]-dp[l-1]$

对应代码：

//3.使用前缀和数组
int l = 0,r = 0;
while(m--)
{cin>>l>>r;// 查询 l 到 r 的区间和cout<<dp[r] - dp[l - 1]<<endl;      
}

复杂度：

• 预处理：$O(n)$
• 每次查询：$O(1)$

---

二、二维前缀和

第二个代码解决的是“二维矩阵子矩阵和”问题。

1. 核心思想

我们将一维前缀和扩展到二维。我们定义一个“二维前缀和数组” dp。
$dp[i][j]$ 存储的是原矩阵 arr 中，以 $(1,1)$ 为左上角、$(i,j)$ 为右下角的子矩阵中所有元素的总和。

2. 如何构建前缀和数组 (预处理)

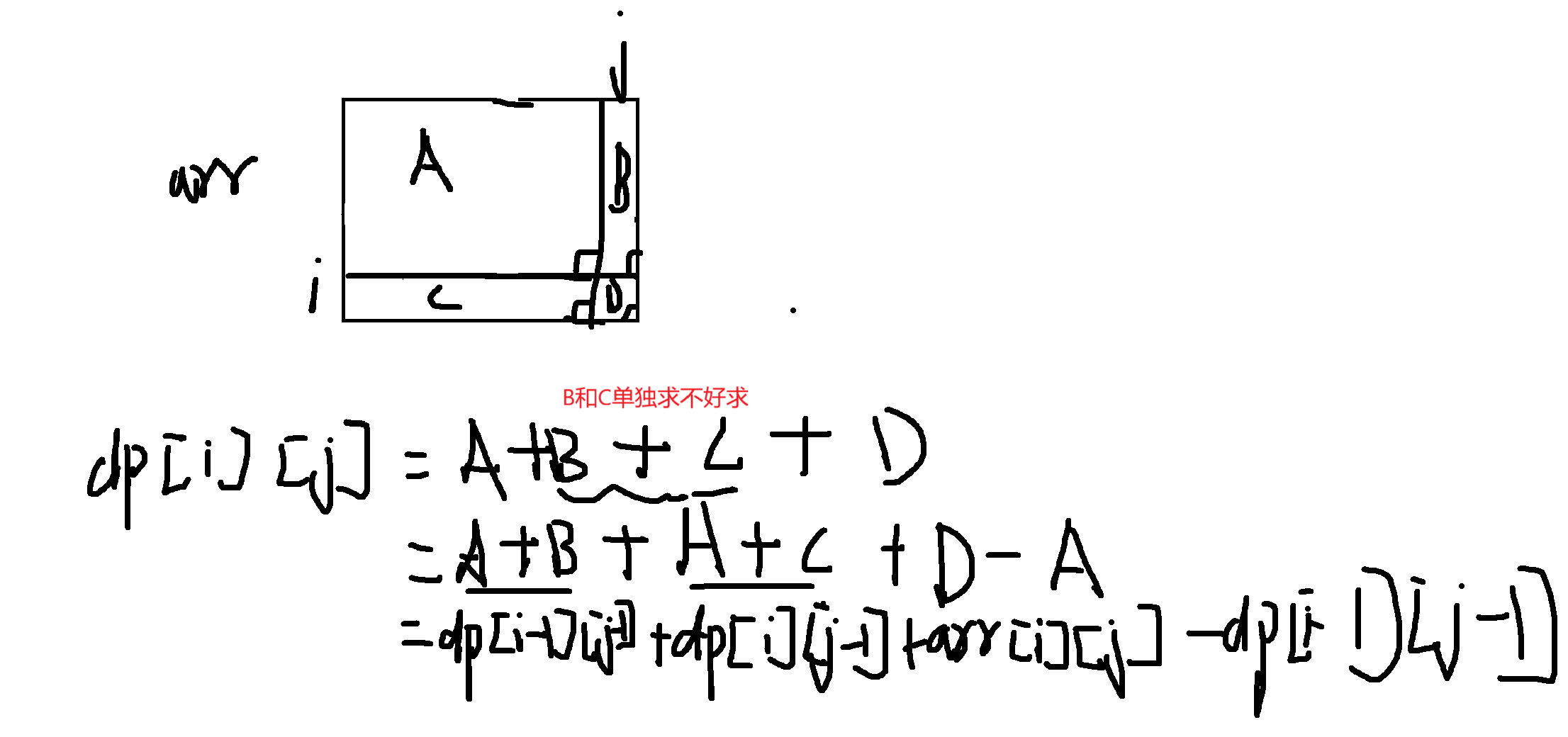
我们使用“容斥原理”来计算 $dp[i][j]$。
$dp[i][j]$ 的值 = 区域A (dp[i-1][j]) + 区域B (dp[i][j-1]) - 重复区域C (dp[i-1][j-1]) + 当前元素值 (arr[i][j])

递推公式为：
$dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+arr[i][j]$

对应代码：

//预处理一个前缀和数组
vector<vector<long long>> dp(n+1,vector<long long>(m+1));
for(int i = 1; i <= n; i++)
{for(int j = 1; j <= m; j++){// 容斥原理计算dp[i][j] = dp[i][j-1] + dp[i-1][j] + arr[i][j] - dp[i-1][j-1];}
}

3. 如何使用前缀和数组 (查询)

如果我们想求以 $(x1,y1)$ 为左上角、$(x2,y2)$ 为右下角的子矩阵的和。

我们同样使用容斥原理：
目标和 = 区域A (dp[x2][y2]) - 区域B (dp[x1-1][y2]) - 区域C (dp[x2][y1-1]) + 区域D (dp[x1-1][y1-1])

查询公式为：
$Sum(x1,y1,x2,y2)=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]$

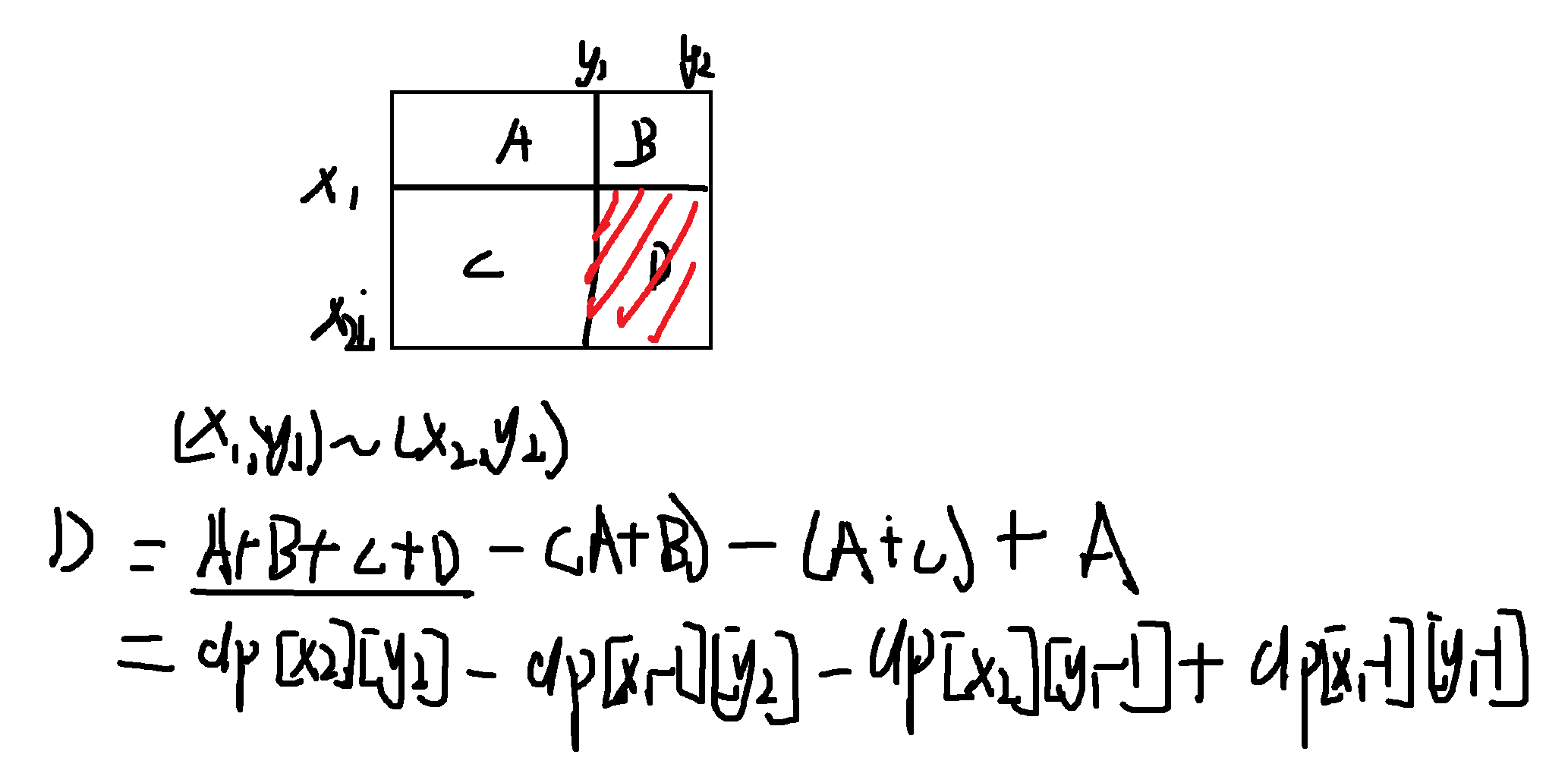
对应代码：

//3.使用前缀和数组
while(q--)
{int x1,x2,y1,y2;cin>>x1>>y1>>x2>>y2;// 容斥原理查询子矩阵和cout<<dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]<<endl;
}

复杂度：

• 预处理：$O(n\times m)$
• 每次查询：$O(1)$

这是另一个巧妙运用“前缀和”思想的例子，用于解决“寻找数组的中心下标” (Pivot Index) 问题。

寻找数组的中心下标（前缀和 + 后缀和）

1. 问题定义

“中心下标” (Pivot Index) 是指这样一个索引：该索引左侧所有元素（不包括该索引自身）的总和，等于该索引右侧所有元素（不包括该索引自身）的总和。

如果数组存在多个中心下标，则返回最左边的那一个。如果不存在，则返回 -1。

2. 核心思想

最直观的暴力解法是：遍历数组中的每一个索引 i，然后对 i 的左侧和右侧分别求和，比较它们是否相等。这种方法的时间复杂度是 $O(n^2)$，效率较低。

你的代码采用了更高效的 “前缀和 + 后缀和” 策略，将时间复杂度优化到了 $O(n)$。

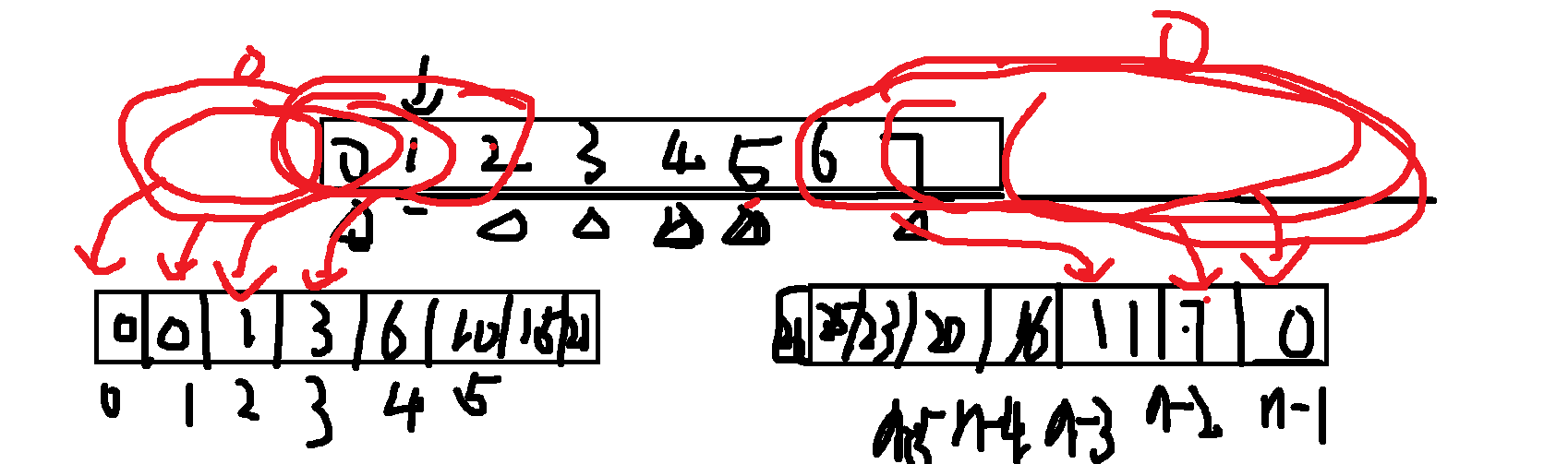
• 前缀和 (Prefix Sum): f[i] 存储索引 i 左侧所有元素的总和。
• 后缀和 (Suffix Sum): g[i] 存储索引 i 右侧所有元素的总和。

如果我们在某处发现 f[i] == g[i]，那么 i 就是我们寻找的中心下标。

3. 算法分解

步骤一：定义前缀和数组 f

• f[i] 被定义为 nums[0] + ... + nums[i-1] 的和。
• 边界情况: f[0] = 0。因为索引 0 的左侧没有任何元素，所以和为 0。
• 递推公式: f[i] = f[i-1] + nums[i-1]。第 i 个索引的左侧和 = (第 i-1 个索引的左侧和) + (元素 nums[i-1])。

对应代码 (预处理前缀和)：

vector<int> f(n);//前缀和数组
f[0] = 0;
for(int i = 1; i < n; i++)
{f[i] = f[i - 1] + nums[i - 1];
}

步骤二：定义后缀和数组 g

• g[j] 被定义为 nums[j+1] + ... + nums[n-1] 的和。
• 边界情况: g[n-1] = 0。因为最后一个元素 (索引 n-1) 的右侧没有任何元素，所以和为 0。
• 递推公式: g[j] = g[j+1] + nums[j+1]。第 j 个索引的右侧和 = (第 j+1 个索引的右侧和) + (元素 nums[j+1])。
  • 注意：这个循环是反向遍历的。

对应代码 (预处理后缀和)：

vector<int> g(n);//后缀和数组
g[n-1] = 0;
for(int j = n - 2; j >= 0; j--)
{g[j] = g[j + 1] + nums[j + 1];
}

步骤三：查找中心下标

经过前两步的预处理，我们现在有了所有索引的左侧和 (存储在 f) 与右侧和 (存储在 g)。

我们只需要遍历一次数组，比较 f[i] 和 g[i] 是否相等即可。

对应代码 (使用前缀和与后缀和)：

for(int i = 0; i < n; i++)if(f[i] == g[i])return i; // 找到，立即返回return -1; // 循环结束都没找到

4. 复杂度分析

• 时间复杂度: $O(n)$。
  • 计算前缀和 $f$ 需要 $O(n)$。
  • 计算后缀和 $g$ 需要 $O(n)$。
  • 遍历比较 $f$ 和 $g$ 需要 $O(n)$。
  • 总共是 $O(n)+O(n)+O(n)=O(n)$。
• 空间复杂度: $O(n)$。
  • 需要 $O(n)$ 的空间存储前缀和数组 f。
  • 需要 $O(n)$ 的空间存储后缀和数组 g。

---

优化：$O(1)$ 空间复杂度解法

这个解法还可以进一步优化，只使用 $O(1)$ 的额外空间。

1. 计算整个数组的总和 totalSum。
2. 遍历数组，维护一个 leftSum 变量，初始为 0。
3. 在索引 i 处：
   • 此时 leftSum 存储的是 i 左侧元素的和。
   • i 右侧元素的和 rightSum 可以通过 totalSum - leftSum - nums[i] 动态计算出来。
   • 比较 leftSum == rightSum：
     • 如果相等，i 就是中心下标，返回 i。
   • 更新 leftSum: leftSum = leftSum + nums[i] (为下一次循环做准备)。
4. 如果遍历结束仍未找到，返回 -1。

这种方法只用到了 totalSum 和 leftSum 两个额外变量，空间复杂度为 $O(1)$。

 int pivotIndex(vector<int>& nums) {int n = nums.size();int totalSum = 0;for(auto e : nums){totalSum += e;}int leftSum = 0;for(int i = 0; i < n; i++){int rightSum = totalSum - leftSum - nums[i];if(leftSum == rightSum)return i;leftSum = leftSum + nums[i];}return -1;}

这道题是 “除自身以外数组的乘积” (Product of Array Except Self)，你的解法非常巧妙，是这道题的标准解法之一，利用了 “前缀积” 和 “后缀积” 的思想。

除自身以外数组的乘积 (前缀积 + 后缀积)

1. 核心思想

题目的要求是 answer[i] 等于 nums 数组中除了 nums[i] 之外所有元素的乘积。

我们可以把这个乘积拆分为两部分：
answer[i] = (i 左侧所有元素的乘积) * (i 右侧所有元素的乘积)

你的代码正是通过预处理，分别计算出这两部分的乘积。

---

2. 预处理 “前缀积数组” (f)

你的 f 数组 vector<int> f(n) 被用来存储 “左侧所有元素的乘积”。

• f[i] 的定义：nums[0] * nums[1] * ... * nums[i-1]。
• 边界情况 f[0] = 1：f[0] 存储 nums[0] 左侧所有元素的乘积。nums[0] 左侧没有元素，空集的乘积在数学上定义为 1（乘法单位元）。
• 递推公式 f[i] = f[i-1] * nums[i-1]：
  • f[i-1] 存储了 nums[0...i-2] 的乘积。
  • f[i] (即 nums[0...i-1] 的乘积) 就等于 f[i-1] * nums[i-1]。

// f[i] 存储 nums[i] 左侧所有元素的乘积
f[0] = 1;
for(int i = 1; i < n; i++)
{f[i] = f[i-1] * nums[i-1];
}

---

3. 预处理 “后缀积数组” (g)

你的 g 数组 vector<int> g(n) 被用来存储 “右侧所有元素的乘积”。

• g[i] 的定义：nums[i+1] * nums[i+2] * ... * nums[n-1]。
• 边界情况 g[n-1] = 1：g[n-1] 存储 nums[n-1] 右侧所有元素的乘积。右侧没有元素，乘积为 1。
• 递推公式 g[i] = g[i+1] * nums[i+1]：
  • g[i+1] 存储了 nums[i+2...n-1] 的乘积。
  • g[i] (即 nums[i+1...n-1] 的乘积) 就等于 g[i+1] * nums[i+1]。
  • (注意：这个循环是反向遍历的)

// g[i] 存储 nums[i] 右侧所有元素的乘积
g[n-1] = 1;
for(int i = n-2; i >= 0; i--)
{g[i] = g[i+1] * nums[i+1];
}

---

4. 组合结果

最后一步，你遍历数组，将 “左侧乘积” 和 “右侧乘积” 相乘，就得到了最终答案。

// ret[i] = f[i] * g[i]
for(int i = 0; i < n; i++)
{// (nums[i]左侧的乘积) * (nums[i]右侧的乘积)ret.push_back(f[i]*g[i]);
}

---

5. 复杂度分析

• 时间复杂度: $O(n)$
  • 第一次 for 循环（计算 f）是 $O(n)$。
  • 第二次 for 循环（计算 g）是 $O(n)$。
  • 第三次 for 循环（计算 ret）是 $O(n)$。
  • 总共是 $O(n)+O(n)+O(n)=O(n)$。
• 空间复杂度: $O(n)$
  • 你使用了 f, g, ret 三个额外的数组，每个数组大小为 $n$。
  • ( 注：这道题可以被优化到 $O(1)$ 的空间复杂度（不包括返回的 ret 数组），方法是复用 ret 数组来充当 f 的角色，并用一个变量来实时计算 g )。

这是 “和为 K 的子数组” (Subarray Sum Equals K) 问题的最优解法之一，它使用了 “前缀和 + 哈希表” 的思想，非常巧妙。

和为 K 的子数组 (前缀和 + 哈希表)

1. 问题定义

给定一个整数数组 nums 和一个整数 k，你需要找到该数组中和为 k 的连续子数组的个数。

2. 核心思想（暴力解法的瓶颈）

• 暴力解法：我们可以用两层 for 循环，枚举所有的子数组 nums[j...i]，并计算它们的和，看是否等于 k。时间复杂度为 $O(n^3)$（枚举 $i,j$ 并求和）或 $O(n^2)$（枚举 $i,j$ 并 $O(1)$ 计算和）。当 $n$ 很大时，会超时。

• 优化思路：我们想在 $O(n)$ 时间内解决问题。

  • 我们定义 前缀和 pre[i] 为 nums[0] + ... + nums[i] 的和。
  • 那么，任意一个子数组 nums[j...i] 的和就可以在 $O(1)$ 时间内算出：
    Sum(j, i) = pre[i] - pre[j-1] (其中 $j\le i$)
  • 我们的目标是寻找有多少个 (i, j) 组合，使得 pre[i] - pre[j-1] = k。
  • 我们将这个等式变形：
    pre[j-1] = pre[i] - k

j-1 代表的是子数组 开始位置（j）的前一个位置。

我们来详细拆解一下：

为什么我们需要 j-1？

我们使用“前缀和数组” pre 来快速计算任意子数组 nums[j...i] 的和。

• pre[i] 的定义是：从开头（索引 0）一直加到索引 i 的总和。
  pre[i] = nums[0] + nums[1] + ... + nums[i]

• Sum(j, i) 的定义是：我们想要的子数组的和。
  Sum(j, i) = nums[j] + nums[j+1] + ... + nums[i]

---

用一个例子来看：

假设数组 nums = [A, B, C, D, E] 索引： 0 1 2 3 4

前缀和 (pre) 数组会是：

• pre[0] = A
• pre[1] = A + B
• pre[2] = A + B + C
• pre[3] = A + B + C + D
• pre[4] = A + B + C + D + E

---

现在，假设我们想求子数组 [C, D] 的和。

1. 这个子数组的起始索引 j = 2 (C的位置)。
2. 这个子数组的结束索引 i = 3 (D的位置)。
3. 我们想要的和是 C + D。

我们怎么用 pre 数组来得到 C + D 呢？

• 步骤 1： 先取到结束位置 i 的所有前缀和。
  pre[i] = pre[3] = A + B + C + D

• 步骤 2： pre[3] 包含了我们不想要的 “前缀” [A, B]。我们必须减掉它。
  (A + B + C + D) - (A + B) = C + D (这就是我们想要的！)

• 步骤 3： 关键来了！我们怎么表示 (A + B) 呢？
  (A + B) 正好是 pre[1]。
  而 1 是什么？
  我们的起始索引 j 是 2。 1 刚刚好就是 j-1 ！

---

结论：

Sum(j, i) = pre[i] - pre[j-1]

• pre[i]： 从开头到子数组结尾的总和。
• pre[j-1]：从开头到子数组开始前一个位置的总和。（这正是我们要减掉的“多余”部分）

3. 算法分解 (前缀和 + 哈希表)

这个变形后的等式是算法的关键：
pre[j-1] = pre[i] - k

• 含义：当我们在 i 位置计算出当前的前缀和 pre[i] (即代码中的 sum) 时，我们只需要回头看：“在 i 之前，有多少个 j-1 位置，其前缀和 pre[j-1] 恰好等于 pre[i] - k？”
• 哈希表的作用：哈希表 hash 就用来存储之前出现过的所有前缀和以及它们各自出现的次数。
  • hash[P] = count 表示：前缀和 P 到目前为止已经出现过了 count 次。

代码逐行分析：

1. unordered_map<int,int> hash;

   • key (int): 存储一个前缀和的值。
   • value (int): 存储该前缀和出现过的次数。

2. int ret = 0; int sum = 0;

   • ret: 最终的结果（和为 k 的子数组个数）。
   • sum: 动态更新的当前前缀和，即 pre[i]。

3. hash[0] = 1; (最关键的初始化)

   • 为什么？ 这是为了处理那些从索引 0 开始的子数组。
   • 举例：如果 nums[0...i] 的和恰好等于 k，即 pre[i] = k。
   • 那么在 i 位置，代码会去查找 hash[sum - k]，也就是 hash[k - k]，即 hash[0]。
   • 如果我们不设置 hash[0] = 1，这个 nums[0...i] 子数组就会被漏掉。
   • hash[0] = 1 的含义是：“前缀和为 0 (即空数组) 已经出现过 1 次了”。

4. for(auto x : nums) (遍历数组)

   • sum += x;

     • 计算当前的前缀和 pre[i]。

   • if(hash.count(sum - k))

     • 检查 hash 中是否存在 pre[i] - k 这个键。
     • 这等同于检查是否存在我们需要的 pre[j-1]。

   • ret += hash[sum - k];

     • 如果存在，说明找到了一个或多个满足条件的 pre[j-1]。
     • hash[sum - k] 的值就是 pre[j-1] 出现的次数，也就是我们能以当前 i 位置为终点、组成和为 k 的子数组的个数。将这个次数累加到 ret。

   • hash[sum]++;

     • 非常重要：在检查完 之后，再将当前的前缀和 sum (即 pre[i]) 存入哈希表（或将其计数加 1）。
     • 这是为了给后续的 i (例如 i+1, i+2... ) 来查找 pre[j-1] 时使用。

4. 复杂度分析

• 时间复杂度: $O(n)$

  • 我们只遍历数组 nums 一次。
  • unordered_map (哈希表) 的插入和查找操作的平均时间复杂度为 $O(1)$。

• 空间复杂度: $O(n)$

  • 在最坏的情况下，n 个前缀和都是不相同的，哈希表需要存储 $n$ 个键值对。

  这道题是 “和可被 K 整除的子数组” (Subarray Sums Divisible by K)，你的代码是这道题的 $O(n)$ 最优解。

int subarraySum(vector<int>& nums, int k) {unordered_map<int,int> hash;int ret = 0;int sum = 0;hash[0] = 1;for(auto x : nums){sum += x;if(hash.count(sum - k)) ret += hash[sum - k];hash[sum]++;}return ret;}

和可被 K 整除的子数组

1. 核心思想 (同余定理)

• 我们定义 pre[i] 为 nums[0] + ... + nums[i] 的前缀和。
• 一个子数组 nums[j...i] (其中 $j\le i$) 的和为 Sum(j, i) = pre[i] - pre[j-1]。
• 我们的目标是找到 Sum(j, i) 能被 k 整除的 (i, j) 组合。
• 用数学公式表示，就是 (pre[i] - pre[j-1]) % k == 0。

根据同余定理，(A - B) % k == 0 等价于 A % k == B % k。

• 因此，我们的目标从 “寻找和为 $k$ 的子数组” (上一题) 转变为了：
  “寻找 pre[i] 和 pre[j-1]，使得它们对 $k$ 取余的结果相同。”

2. 算法分解 (前缀和 + 哈希表)

我们使用一个哈希表 hash 来存储前缀和的余数以及该余数出现的次数。

• hash[R] = count 意味着：到目前为止，余数为 R 的前缀和已经出现过了 count 次。

代码逐行分析：

1. unordered_map<int,int> hash;

   • key (int): 存储 pre[i] % k 的余数 R。
   • value (int): 存储余数 R 已经出现过的次数。

2. int sum = 0; int ret = 0;

   • sum: 动态更新的当前前缀和 pre[i]。
   • ret: 结果计数器。

3. hash[0] = 1; (关键初始化)

   • 与上一题 hash[0] = 1 意义相同。
   • 它表示 “余数为 0 的前缀和” 已经出现过 1 次了（即 pre[-1]，代表空数组）。
   • 这是为了正确统计那些从索引 0 开始并且其和本身就能被 k 整除的子数组（例如 pre[i] % k == 0）。

4. for(auto x : nums) (遍历数组)

   • sum += x;

     • 计算当前的前缀和 pre[i]。

   • int R = (sum % k + k) % k; (处理负数余数)

     • 这是本题的第二个关键点。
     • 在 C++ 中，负数的模运算 % 可能会得到负余数 (例如 -1 % 5 == -1)。
     • 我们希望余数始终在 [0, k-1] 的范围内。
     • sum % k：可能为负 (例如 -1)。
     • sum % k + k：保证结果非负 (例如 -1 + 5 = 4)。
     • (sum % k + k) % k：将结果拉回到 [0, k-1] 范围内 (例如 (4 % 5 + 5) % 5 = 4； (5 % 5 + 5) % 5 = 0)。
     • R 就是 pre[i] 对 k 取模的 “数学余数”。

   • if(hash.count(R)) 和 ret += hash[R];

     • 我们检查哈希表中是否已经存在这个余数 R。
     • 如果存在，hash[R] 的值代表在 i 之前，有 hash[R] 个 pre[j-1] 也具有相同的余数 R。
     • 根据同余定理，每一个这样的 pre[j-1] 都能与当前的 pre[i] 组合，形成一个和能被 k 整除的子数组 nums[j...i]。
     • 因此，我们将 hash[R] 累加到 ret 中。

   • hash[R]++;

     • 在检查完 之后，我们将当前这个余数 R 的出现次数加 1。
     • 这是为了给后续的 pre[i] (例如 i+1, i+2... ) 提供 pre[j-1] 的查找数据。

问得非常好！你已经抓住了 “前缀和” 思想的精髓。

在 subarraySum (和为 K) 问题中，我们是这样 “去掉” 前缀和的：
pre[i] - pre[j-1] = k
我们用减法来找到 k。

---

在 subarraysDivByK (被 K 整除) 问题中，我们 “去掉” 前缀和的方式非常不一样。我们不是在找一个固定的 k，而是在找一个能被 k 整除的数。

我们来看看 pre[i] - pre[j-1] 到底是什么。

假设 k = 5。

1. pre[i] (当前的总和) = 17

   • 17 除以 5，等于 3 … 余 2。
   • 我们可以把 17 看作：(3 * 5) + 2

2. pre[j-1] (你想“去掉”的前缀) = 7

   • 7 除以 5，等于 1 … 余 2。
   • 我们可以把 7 看作：(1 * 5) + 2

现在，我们把它们减掉 (即 “去掉” 不想要的 pre[j-1] )： pre[i] - pre[j-1] = 17 - 7 = 10 10 可以被 5 整除！我们找到了一个答案。

我们再看看用 “余数” 的方式来减： pre[i] - pre[j-1] = ( (3 * 5) + 2 ) - ( (1 * 5) + 2 ) = (3 * 5) - (1 * 5) + (2 - 2) = (3 - 1) * 5 + 0 = 2 * 5

你发现了吗？

当我们把两个余数相同的数相减时，它们的余数部分 (2 - 2) 相互抵消了，只剩下了 k 的倍数部分 (`(3 - 1)

• 5`)。

---

结论：

在这道题里，“去掉” pre[j-1] 的方法，就是去寻找一个 pre[j-1]，它除以 k 的余数和 pre[i]
除以 k 的余数是完全相同的。

• pre[i] = (某个 k 的倍数) + 余数R
• pre[j-1] = (某个 k 的倍数) + 余数R (相同的余数)

当你用 pre[i] 减去 pre[j-1] 时： pre[i] - pre[j-1] = ( k 的倍数A - k
的倍数B ) + ( 余数R - 余数R ) = (k 的倍数C) + 0 = k 的倍数C

所以，pre[i] - pre[j-1] 一定能被 k 整除！

---

我的代码是如何做到“去掉”的：

if(hash.count((sum%k+k)%k)) ret += hash[(sum%k+k)%k];
hash[(sum%k+k)%k]++;

1. R = (sum%k+k)%k：你计算出当前 pre[i] 的余数 R。
2. ret += hash[R]：你是在说：“快去哈希表里帮我查一查，以前有多少个 pre[j-1] 也留下了这个余数 R？”
3. 哈希表告诉你：“有 count 个 ( hash[R] 的值)！”
4. ret += count：你就知道，当前的 pre[i] 可以和这 count 个 pre[j-1] 分别配对，形成 count 个和能被 k 整除的子数组。
5. hash[R]++：最后，你把你自己 (当前的 pre[i] 和它的余数 R) 也登记到哈希表里，告诉它：“余数 R 的大家庭又多了一个成员！”，这样以后的 pre[x] 就可以来找你了。

*一句话总结：在这道题里，“寻找相同余数”就等价于“去掉不想要的前缀和”。

3. 复杂度分析

• 时间复杂度: $O(n)$
  • 我们只遍历数组 nums 一次。
  • unordered_map (哈希表) 的插入和查找操作的平均时间复杂度为 $O(1)$。
• 空间复杂度: $O(k)$
  • 哈希表中最多只会存储 k 个键（余数 0 到 k-1）。这优于上一题的 $O(n)$ 空间复杂度。

int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int> hash;int sum = 0;int ret = 0;hash[0] = 1;for(auto x : nums){sum += x;//当前前缀和数组if(hash.count((sum%k+k)%k))ret += hash[(sum%k+k)%k];hash[(sum%k+k)%k]++;}return ret; }

连续数组

1. 核心思想：问题转换

• 问题：找到一个最长的子数组，其中 0 和 1 的个数相等。
• 转换：如果我们把 0 视作 -1，1 视作 +1。
  • [0, 1, 0, 1] 就变成了 [-1, 1, -1, 1]。
  • “0 和 1 个数相等” 的子数组，就变成了 “和为 0” 的子数组。
• 新问题：找到一个最长的、和为 0 的子数组。

2. 算法：前缀和 + 哈希表 (求最大长度)

这个问题和 “和为 K 的子数组” ( subarraySum ) 非常相似，但有两个关键区别：

1. 目标 k 固定为 0。
2. 我们求的是最大长度，而不是个数。

我们用 sum 表示 “前缀和” ( pre[i] )。
如果 pre[i] - pre[j-1] = 0，则 pre[i] == pre[j-1]。

• 哈希表 hash 的作用：

  • key (int): 出现过的前缀和 sum。
  • value (int): 该前缀和第一次出现的索引 i。

• 目标：当我们在 i 位置计算出 sum 时，我们回头看：“这个 sum 以前出现过吗？”

  • 如果它在 j 位置出现过 ( hash[sum] = j )，
  • 这意味着 pre[i] == pre[j]。
  • 根据前缀和原理，nums[j+1 ... i] 这个子数组的和一定是 0。
  • 这个子数组的长度就是 i - j。

3. 代码逐行分析

 sum += nums[i] == 0 ? -1 : 1;

这就是核心的 “问题转换”。在遍历时，遇到 0 就减 1，遇到 1 就加 1。

---

 hash[0] = -1;(最关键的初始化)

• 为什么是 -1？
  • 这和 subarraySum 里的 hash[0] = 1 是一个道理，都是为了处理从索引 0 开始的子数组。
• 举例：nums = [0, 1]，转换后是 [-1, 1]。
  • i = 0：sum = -1。 hash[-1] = 0。
  • i = 1：sum = 0。
  • 此时，代码会查找 hash[0]。
  • 我们希望计算长度 i - j。这里的 i 是 1，而 j 应该是 “虚拟” 的开始位置 -1。
  • 长度 i - hash[0] = 1 - (-1) = 2。
• 含义：hash[0] = -1 意思是：“前缀和为 0 的情况”在索引 -1 (即数组开始前) 就已经出现过了。

---

 if(hash.count(sum))(找到匹配)

• 含义：如果为 true，说明当前的 sum 在过去已经出现过了。
• 假设 hash[sum] 存的是 j， j 是第一次出现这个 sum 时的索引。
• pre[i] (当前) == pre[j] (过去)。
• 这说明 nums[j+1 ... i] 这个子数组的和为 0。
• ret = max(ret, i - hash[sum]);
  • i - hash[sum] 就是子数组 [j+1 ... i] 的长度。
  • 我们用 max 来保留我们找到过的最大长度。

---

 else { hash[sum] = i; } (存储首次出现)

• 为什么要有 else？
  • 因为我们要求的是最大长度。
  • i - j 要最大，i 肯定是越大越好 (即当前索引)，而 j ( hash[sum] ) 必须是越小越好。
  • 所以，我们只在哈希表中存储第一次 (最左边) 遇到这个 sum 时的索引 i。如果后面又遇到了这个 sum，我们不再更新 hash[sum] 的值，而是用那个旧的、最小的 j 来计算长度。

4. 复杂度分析

• 时间复杂度: $O(n)$
  • 我们只遍历数组 nums 一次。
  • unordered_map (哈希表) 的插入和查找操作的平均时间复杂度为 $O(1)$。
• 空间复杂度: $O(n)$
  • 在最坏的情况下，n 个前缀和都是不相同的，哈希表需要存储 $n$ 个键值对。

int findMaxLength(vector<int>& nums) {unordered_map<int,int> hash;int sum = 0;int ret = 0;hash[0] = -1;for(int i = 0; i < nums.size(); i++){sum += nums[i] == 0 ? -1 : 1;//if(hash.count(sum)){ret = max(ret,i - hash[sum]);}else{hash[sum] = i;} }return ret; }

矩阵区域和 (二维前缀和)

1. 核心思想 💡

• 问题：要求 answer[i][j] 是 mat[i][j] 周围 k 范围内所有元素的总和。
• 暴力解法：对 answer 矩阵中的每一个 (i, j)，都遍历一遍 (2k+1) x (2k+1) 的方块并求和。这会非常慢，时间复杂度高达 $O(m\times n\times k^2)$。
• 优化解法：使用二维前缀和。
  1. 预处理 (O(m*n))：创建一个 dp 矩阵，dp[i][j] 存储原矩阵 mat 中从 (0, 0) 到 (i-1, j-1) 的矩形区域内所有元素的总和。
  2. 查询 (O(1))：利用 dp 矩阵，可以在 $O(1)$ 的时间内查询 mat 中任意一个矩形区域的和。

---

2. 算法分解

你的代码完美地执行了这两个步骤。

步骤一：预处理 (构建 dp 数组)

dp 数组的大小是 (m+1) x (n+1)，这是一种常见的技巧，通过增加一行一列 “哨兵”（全为0），来简化边界条件的处理。

dp[i][j] 存储的是 mat 数组中，以 mat[0][0] 为左上角，mat[i-1][j-1] 为右下角的矩形和。

// 预处理二维前缀和
for(int i = 1;i <= m; i++)
{for(int j = 1; j <= n; j++){// 核心公式（容斥原理）dp[i][j] = dp[i-1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i-1][j-1];}
}

• 公式解释：
  • dp[i-1][j]：上方的矩形区域和。
  • dp[i][j-1]：左方的矩形区域和。
  • mat[i-1][j-1]：当前 (i, j) 对应的原矩阵 mat 中的值。
  • dp[i-1][j-1]：左上方的矩形区域和。
  • 由于 “上方” 和 “左方” 都包含了 “左上方” 区域，所以 dp[i-1][j-1] 被加了两次，必须减去一次。

---

步骤二：查询 (计算 answer 数组)

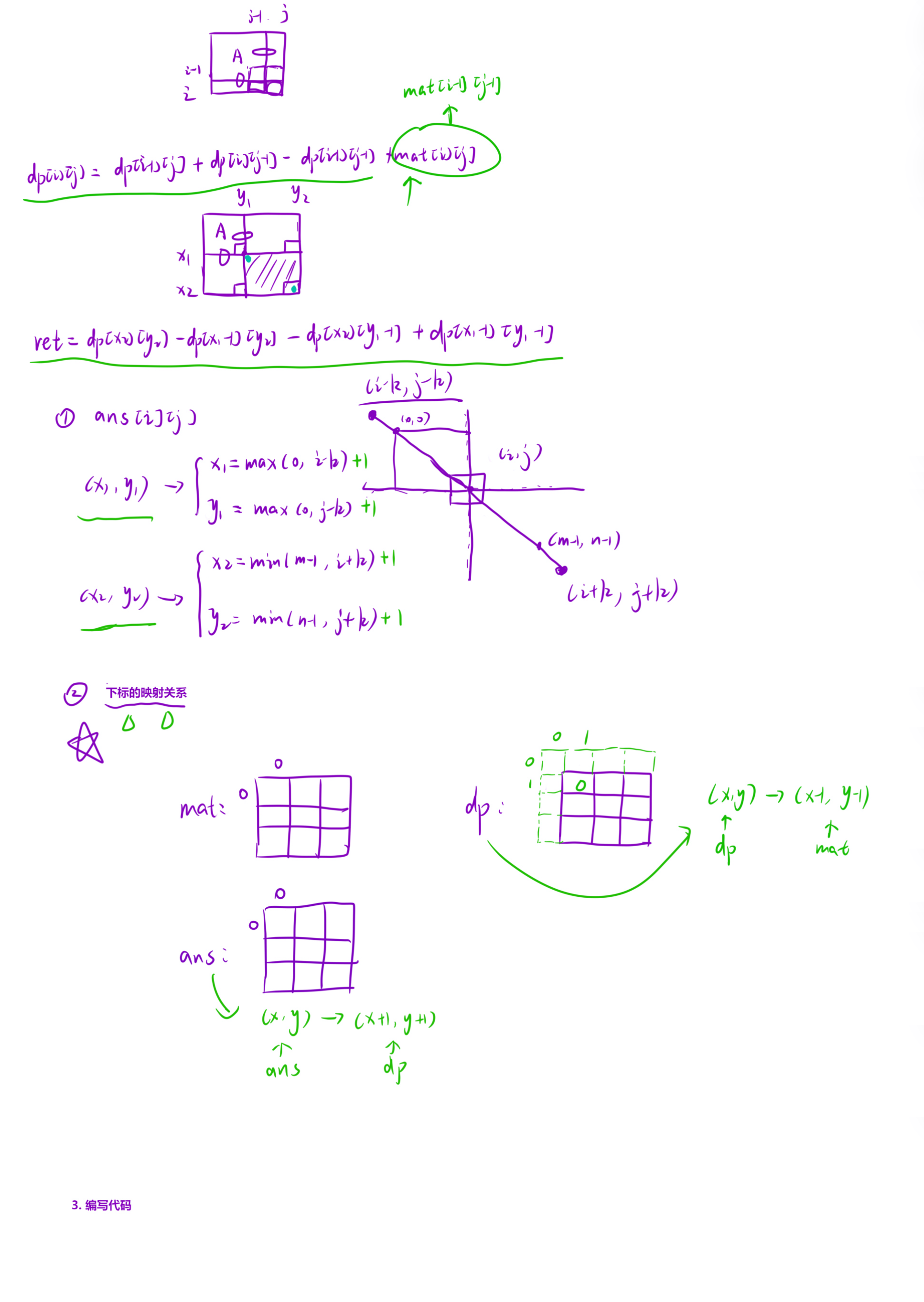
这一步是遍历 answer 矩阵的每个 (i, j)，计算它对应的 “方块和”。

1. 确定方块边界 (Bounding Box) 🎯
对 answer[i][j]，我们需要的 mat 矩阵的范围是：

• 行：从 r1 = i-k 到 r2 = i+k
• 列：从 c1 = j-k 到 c2 = j+k

但是，这些索引不能超出 mat 的边界 [0, m-1] 和 [0, n-1]。所以我们要 “裁剪” (clamp) 它们：

• r1_clipped = max(0, i-k)
• c1_clipped = max(0, j-k)
• r2_clipped = min(m-1, i+k)
• c2_clipped = min(n-1, j+k)

2. 转换为 dp 数组的 1-based 索引 🔢
我们的 dp 数组是 1-based 索引（dp[1][1] 对应 mat[0][0]）。要查询 mat 中 (r, c) 对应的矩形，我们需要 dp 索引 (r+1, c+1)。

所以，我们需要的 dp 坐标是：

• x1 = r1_clipped + 1 => max(0, i-k) + 1
• y1 = c1_clipped + 1 => max(0, j-k) + 1
• x2 = r2_clipped + 1 => min(m-1, i+k) + 1
• y2 = c2_clipped + 1 => min(n-1, j+k) + 1
  这完全对应你代码中的 x1, y1, x2, y2。

3. 使用前缀和公式查询 📊
现在我们有了方块的左上角 (x1, y1) 和右下角 (x2, y2)（在 dp 的 1-based 索引下），我们用 $O(1)$ 的查询公式来获取这个方块的和：

// 核心查询公式（容斥原理）
answer[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];

• 公式解释：
  • dp[x2][y2]：从 (0,0) 到 (x2, y2) 的总和。
  • - dp[x1-1][y2]：减去目标方块上方的矩形。
  • - dp[x2][y1-1]：减去目标方块左侧的矩形。
  • + dp[x1-1][y1-1]：由于 “上方” 和 “左侧” 都减去了 “左上方” 的矩形，我们必须加回来一次。
    

---

3. 复杂度分析

• 时间复杂度：$O(m\times n)$
  • 预处理 dp 数组花了 $O(m\times n)$。
  • 遍历 answer 数组花了 $O(m\times n)$，但每次查询都是 $O(1)$。
  • 总共是 $O(m\times n)+O(m\times n)=O(m\times n)$。
• 空间复杂度：$O(m\times n)$
  • 需要 $O(m\times n)$ 的空间来存储 dp 数组。

vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size();int n = mat[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));vector<vector<int>> answer(m,vector<int>(n));for(int i = 1;i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i-1][j-1];}}for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){int x1 = max(0,i-k)+1,y1 = max(0,j-k)+1;int x2 = min(m-1,i+k)+1,y2 = min(n-1,j+k)+1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];}}return answer;}