数据结构系列之二叉树

---

前言

二叉树是一棵比较重要的树了，后面堆、搜索二叉树、红黑树、AVL树、甚至算法里的线段树，它们的基础都是二叉树，所以二叉树比较重要，需要掌握

---

一、什么是二叉树

二叉树是一颗树，可以为空，由左子树，右子树，根组成, 二叉树不存在度大于2的节点，当然，左子树和右子树都可以不存。

一些特殊的树：
1.满二叉树: 除了叶子节点，每一层的节点都有左右孩子，这就是满二叉树，深度为h，一层的节点个数为2 ^ h.

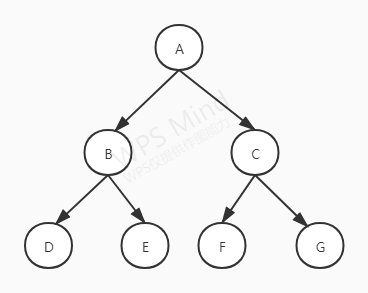
2.完全二叉树
堆的结构里提到了，每一个节点都能与深度相同的满二叉树中1到n的节点相对，就是完全二叉树，满二叉树也是一种完全二叉树

二、一些性质

1.对于任何一棵二叉树，如果它的度为0的节点个数为n0，度为2的节点的个数为n2，则n0 = n2 + 1
这里简单推导一下，设度为0,1,2的节点个数分别为n0,n1,n2，我们知道树的性质有一条是节点的个数 = 度数 + 1，所以： n0 + n1 + n2 = 0 * n0 + 1 * n1 + 2 * n2 + 1,推导出n0 = n2 + 1

还有一些简单性质想一想就明白了，比如第i层的节点个数最多是多少，n个节点的满二叉树的深度是多少… … …懒得说了

2.对于完全二叉树用i开始编号，则有：
i == 0,为根节点
i >0 , i节点父亲的序号， (i - 1) / 2,
如果2 * i + 1 < n ,左孩子的序号， 反之没有左孩子
如果2 * i + 2 < n ,右孩子的序号， 反之没有右孩子

---

三、二叉树的存储结构

二叉树可以分为两种结构存储，一种是顺序结构，一种是链式结构

1.顺序存储

顺序存储就是使用数组来存储，一般只适用于完全二叉树，也就是堆可以使用，对于非完全二叉树不适用，不适用的原因就是空间浪费太多。

2.链式存储

就是上次树中提到的二叉链和三叉链

//二叉链 
struct Node{struct Node* _firstchild; //左孩子  struct Node* _rightchild; //右孩子  int _val; //这里可以任意类型，换成宏就可以 
};//三叉链 
struct Node{struct Node* _parent;     //父亲 struct Node* _firstchild; //左孩子  struct Node* _rightchild; //右孩子  int _val; //这里可以任意类型，换成宏就可以 
};

四、二叉树的操作

想要操作首先就需要创建一棵二叉树，怎么创建？？？这里我们先手动创建，真正的方式其实是前序来创建，销毁也是后序来销毁，介绍完前后序再来。

手动创建二叉树

这里返回的节点就是根节点

BTNode* BuyNode(BTDATATYPE x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
BTNode* CreateTree()
{ BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node3->left = node7;return node1;}

前序遍历、中序遍历、后序遍历

堆里介绍了，前序就是以根、左子树、右子树的方式来遍历，中序就是左子树、根、右子树，后序就是左子树、右子树、根。 其中我们采用递归使用比较简单，有两个遍历后的结果就可以复原树(不可以缺少中序).

前序
void PrevOrder(BTNode *root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
中序
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
后序
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

层序遍历

层序遍历就是一层一层遍历，这里我们用到了队列，用下面这棵树介绍一下操作

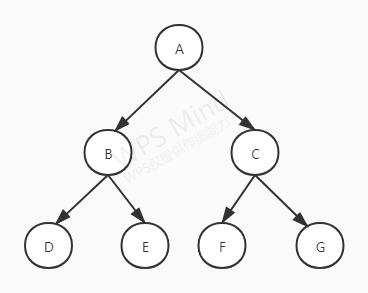
如果根不为空，队列入A，直到队列的size为0为止，取出front打印值并front掉，如果front的左子树存在，入队，front的右子树存在，入右子树。

void LevelOrder(BTNode* root)
{queue<BTNode*> q;if(root != nullptr) {q.push(root);}while(q.size()){BTNode* t = q.front();q.pop();cout << t->data << ' ';if(t->left) q.push(t->left);if(t->right)q.push(t->right);	} }

如果想一层一层的打印出来怎么办？？？就是打印一层然后换行，控制一下出的节点个数就好了，每一次拿到q.size之后，控制一次就出q.size次，操作完更新q.size，就是套一层for循环就好了，在while里面套一层for

void LevelOrder(BTNode* root)
{queue<BTNode*> q;if(root != nullptr) {q.push(root);}int qsize = 1;while(q.size()){for(int i = 0;i < qsize;++i){BTNode* t = q.front();q.pop();cout << t->data << ' ';if(t->left) q.push(t->left);if(t->right)q.push(t->right);}cout << endl;qsize = q.size(); } }

前序遍历创建二叉树

创建出来什么树完全会按照递归的逻辑来，随机插入节点等等。
为什么用前序遍历来创建？？？？？先看代码再解释.

这里我认为中序或者后序无法创建二叉树，因为无法确定根节点，只有前序可以。如果有意见不同者可以评论

创建二叉树

void PrevCreateTree(BTNode*& node)
{char ch;do {ch = getchar();} while (isspace(ch)); if(ch == '#') node = nullptr; else{node = BuyNode(ch - '0');printf("输入左子树的值,输入#表示左子树为空\n");PrevCreateTree(node->left);printf("输入右子树的值,输入#表示右子树为空\n");PrevCreateTree(node->right);}
}

前序构建完全二叉树，n就表示一共几个节点，像上面那样改也可以，但是这个代码构建出来的顺序和自己输入的不同

void PrevCreateTree(BTNode*& node,int n)
{if(n == 0){node = nullptr;return ;}int x;cin >> x;node = BuyNode(x);int m = n - 1;int left_m = m / 2;int right_m = m - left_m;PrevCreateTree(node->left,left_m);PrevCreateTree(node->right,right_m);
}

求高度

高度还是很简单的，求出左右子树的高度，哪个高返回哪个加一，转换成子问题，用递归。

int TreeHeight(BTNode* root)
{if (root == nullptr){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}

求size

size和高度的逻辑差不多，就是存在就++

int TreeSize(BTNode* root)
{return root == nullptr ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

这样也行，看着和高度的逻辑一样

int TreeSize(BTNode* root)
{if(root == nullptr){return 0;}int leftSize = TreeSize(root->left);int rightSize = TreeSize(root->right);return leftSize + rightSize + 1;
}

查找值为x的节点

核心逻辑就是先看看根是不是，根不是就看左子树，左子树不是就看右子树

BTNode* Find(BTNode* root, int x)
{if (root == nullptr){return nullptr;}if (root->data == x){return root;}BTNode* lret = Find(root->left, x);if (lret){return lret;}BTNode* rret = Find(root->right, x);if (rret){return rret;}return nullptr;
}

根的第K层个数

核心逻辑：根的第k层个数=根的左子树的第k-1层个数+根的右子树的第k-1层个数，还是很好理解的，根的左子树多了一层所以就是左子树的k - 1层，注意k == 1表示只有第一层，一定是1

int TreeKLevel(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

删除

删除的逻辑就是和创建相反就可以，后序删除就行。

void Destroy(BTNode*root)
{if(root == nullptr){return ;}Destroy(root->left);Destroy(root->right);cout << root->data <<  "被销毁"<<endl; free(root);
}

总结

二叉树的东西很多，特别是递归的玩法让人很不适应，需要掌握，下次直接更新所有的排序算法。