2.单智能体强化学习
2. 单智能体强化学习
2.1 简介
强化学习是学习状态和行为之间的映射关系,以使得数值回报达到最大化。在未知采取何种行为的情况下, 学习 者必须通过不断尝试才能发现采取哪种行为能够产生最大回报。 这些行为不仅会影响直接回报, 还会影响到下一状态以及后续所有的回报。属于交互式学习。
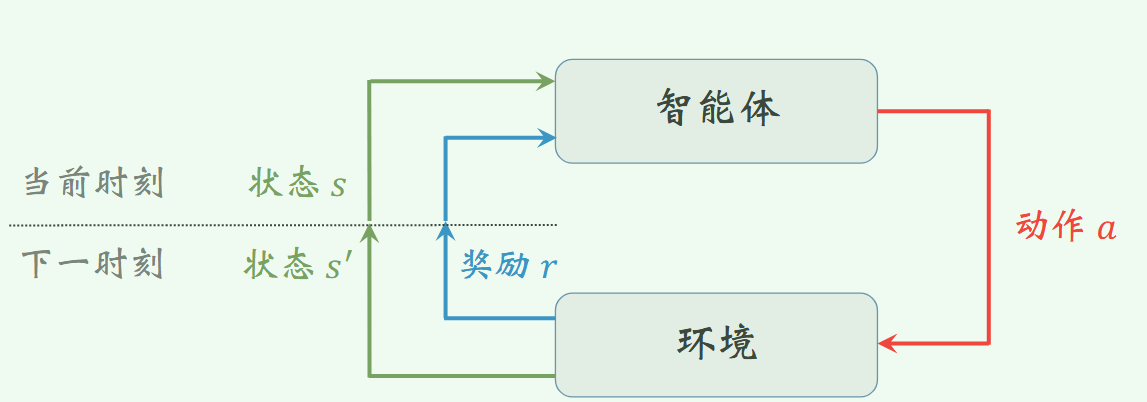
假设在一个离散的时间序列t=0,1,2,⋯t=0,1,2,\cdotst=0,1,2,⋯。在每一个时刻t,智能体能从环境中接收一个状态sts_tst.
定义ata_tat表示智能体在时刻t所采取的行为。在下一个时刻,a_t作为智能体行为的结果,然后接收数值汇报rt+1∈Rr_{t+1}\in\mathfrak{R}rt+1∈R并移动到新状态st+1s_{t+1}st+1。在每一时刻, 智能体完成从状态到每种可能行为的选择概率之间的映射,该映射关系称为策略,记为πt\pi_tπt,则πt(s,a)\pi_t(s,a)πt(s,a)为st=ss_t=sst=s时刻at=aa_t=aat=a的概率。强化学习方法具体反映了智能体如何根据其经验改变策略, 使得在长期运行过程中接收的回报总量达到最大化。
可以在随机博弈框架下研究强化学习问题。这一框架包含两个更为间的框架:马尔可夫决策过程和矩阵博弈。
2.2. n臂赌博机问题
该问题详细内容可以参考链接Lec 5: 多臂老虎机算法基础与应用 - NoughtQ的笔记本

基本思路:
假设n臂老虎机的实际回报分布为
Q⋆(a)=[−0.41.30.040.53−0.15−1.010.21.480.36−0.5]Q^\star(a)=[-0.4\quad1.3\quad0.04\quad0.53\quad-0.15\quad-1.01\quad0.2\quad1.48\quad0.36\quad-0.5 ]Q⋆(a)=[−0.41.30.040.53−0.15−1.010.21.480.36−0.5]
我们希望机器能够学习到Q⋆(7)=1.48Q^\star(7)=1.48Q⋆(7)=1.48。
这个时候设置探索率为ϵ=0.2\epsilon=0.2ϵ=0.2。这意味着,在任意给定选择的情况下,随机选到该策略的概率是0.2.
下面开始按照一个估计的初值开始训练,先假设回报的分布是:
Qe=[0.050.86−0.960.731.98−1.19−0.660.821.97−0.13]Q_{e}=[0.05\quad0.86\quad-0.96\quad0.73\quad1.98\quad-1.19\quad-0.66\quad0.82\quad1.97\quad-0.13]Qe=[0.050.86−0.960.731.98−1.19−0.660.821.97−0.13]
那么按照估计的回报,必然会选择动作4(从0开始索引),因为按照估计QeQ_eQe此时的Qe(4)=1.98Q_e(4)=1.98Qe(4)=1.98,但是真实的回报Q⋆(4)=−0.15Q^\star(4)=-0.15Q⋆(4)=−0.15,也就是说,机器选择策略4最终获得的回报是一个期望为=-0.15,方差为1的N(-0.15,1)随机分布,所以假设机器得到的回报为Q1(4)=−0.76Q_1(4)=-0.76Q1(4)=−0.76
此时,机器按照如下公式更新:
Qt(a)=r1+r2+⋯+rkkQ_t(a)=\frac{r_1+r_2+\cdots+r_k}{k}Qt(a)=kr1+r2+⋯+rk
得到新的估计值
Qe2=[0.050.86−0.960.73−0.76−1.19−0.660.821.97−0.13]Q_{e2}=[0.05\quad0.86\quad-0.96\quad0.73\quad-0.76\quad-1.19\quad-0.66\quad0.82\quad1.97\quad-0.13]Qe2=[0.050.86−0.960.73−0.76−1.19−0.660.821.97−0.13]
接着重复上述过程,一直到逼近实际的奖励分布Q⋆Q^{\star}Q⋆
2.3 学习结构
具体内容参照本人强化学习栏目中的文章。1.强化学习的相关概念-强化学习笔记1_dense reward-CSDN博客
- 在某些情况下,存在一个特定行为使其在特定状态下具有某种意义上的最优。 有时会称这一行为为贪婪行为, 而智能体在各个状态下应最优选择的一组行为称为行为规则或策略
- 如果在某一特定状态下智能体应选择相应的特定行为, 则称之为纯策略, 然而如果智能体以某一特定概率来选择一个行为, 则称之为分布式策略或混合策略。
- 若当前状态是能够对下一步或未来行为进行决策所需的全部条件, 则称该决策系统具有马尔科夫特性。下一步行为与过去行为无关, 而只取决于系统当前所处状态。
2.4 值函数
可参考强化学习(3)_强化学习动作价值函数-CSDN博客
- 值函数(状态价值函数)定义了一个特定状态的价值程度。 衡量一个给定状态的价值程度是基于从该状态可获得的未来期望回报。
Vπ(S)=Eπ{Rt∣st=s}=Eπ{∑k=0∞γkrt+k+1∣st=s}V^\pi(S)=E_\pi\{R_t|s_t=s\}=E_\pi\{\sum^\infty_{k=0}\gamma^kr_{t+k+1}|s_t=s\}Vπ(S)=Eπ{Rt∣st=s}=Eπ{k=0∑∞γkrt+k+1∣st=s} - 动作价值函数,表示在状态sss下选择行为aaa并随后采用规则或策略π\piπ所获得的期望回报。
Qπ(s,a)=Eπ{Rt∣st=s,at=a}=Eπ{∑k=0∞γkrt+k+1∣st=s,at=a}Q^\pi(s,a)=E_\pi\{R_t|s_t=s,a_t=a\}=E_\pi\{\sum^\infty_{k=0}\gamma^kr_{t+k+1}|s_t=s,a_t=a\}Qπ(s,a)=Eπ{Rt∣st=s,at=a}=Eπ{k=0∑∞γkrt+k+1∣st=s,at=a}
2.5 最优动作价值函数
可参考强化学习(3)_强化学习动作价值函数-CSDN博客
Q⋆(s,a)=E{rt+1+γmaxa′Q⋆(st+1,a′)∣st=s,at=a}Q^\star(s,a)=E\{r_{t+1}+\gamma \max_{a'}Q^\star(s_{t+1},a')|s_t=s,a_t=a\}Q⋆(s,a)=E{rt+1+γa′maxQ⋆(st+1,a′)∣st=s,at=a}
网络世界中的示例
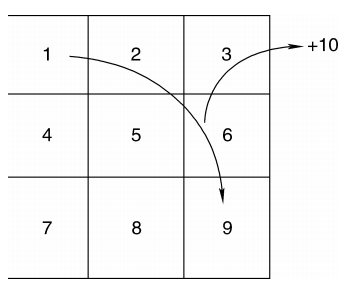
将以一个 3×33 \times 33×3 网格为例,如上图所示。在任意起始时刻,机器人或智能体可位于 9 个单元格之一。接下来,从集合 a∈[up,down,right,left]a \in [\text{up}, \text{down}, \text{right}, \text{left}]a∈[up,down,right,left] 中选择行为。
规则如下:
- 一旦机器人或学习智能体移动到单元格 1,则会立即跳转到单元格 9 并得到回报 r=+10r = +10r=+10。
- 若智能体到达边界,则会停留在当前单元格并得到惩罚 r=−1r = -1r=−1。
- 未来回报的折扣因子 γ=0.9\gamma = 0.9γ=0.9
- 行为选择策略 π(s,a)=0.25\pi(s, a) = 0.25π(s,a)=0.25。
也就是说,智能体将以相同概率任意选择向上、向下、向左或向右。即有 4 种可能行为可实现从某一特定状态转移。只有当智能体移动到状态 1 且以 100% 概率跳转到状态 9 时才会得到 +10+10+10 唯一回报。即除了 r19up=10r_{19}^{\text{up}} = 10r19up=10、r19down=10r_{19}^{\text{down}} = 10r19down=10、r19left=10r_{19}^{\text{left}} = 10r19left=10、r19right=10r_{19}^{\text{right}} = 10r19right=10 之外,其余回报均为 0。
[下标19表示状态有状态1变为状态9]
另外,当智能体到达边界时,
r22up=−1r_{22}^{\text{up}} = -1r22up=−1、r33up=−1r_{33}^{\text{up}} = -1r33up=−1、r33right=−1r_{33}^{\text{right}} = -1r33right=−1、r44left=−1r_{44}^{\text{left}} = -1r44left=−1、r66right=−1r_{66}^{\text{right}} = -1r66right=−1、r77down=−1r_{77}^{\text{down}} = -1r77down=−1、r77left=−1r_{77}^{\text{left}} = -1r77left=−1、r99down=−1r_{99}^{\text{down}} = -1r99down=−1、r99right=−1r_{99}^{\text{right}} = -1r99right=−1。
转移概率如下:
P19up=1,P19down=1,P19left=1,P19right=1P22up=1,P25down=1,P21left=1,P23right=1P33up=1,P36down=1,P32left=1,P33right=1P41up=1,P47down=1,P44left=1,P45right=1P52up=1,P58down=1,P54left=1,P56right=1P63up=1,P69down=1,P65left=1,P66right=1P74up=1,P77down=1,P77left=1,P78right=1P85up=1,P88down=1,P87left=1,P89right=1P96up=1,P99down=1,P98left=1,P99right=1\begin{aligned} &P_{19}^{\text{up}} = 1,\ P_{19}^{\text{down}} = 1,\ P_{19}^{\text{left}} = 1,\ P_{19}^{\text{right}} = 1 \\ &P_{22}^{\text{up}} = 1,\ P_{25}^{\text{down}} = 1,\ P_{21}^{\text{left}} = 1,\ P_{23}^{\text{right}} = 1 \\ &P_{33}^{\text{up}} = 1,\ P_{36}^{\text{down}} = 1,\ P_{32}^{\text{left}} = 1,\ P_{33}^{\text{right}} = 1 \\ &P_{41}^{\text{up}} = 1,\ P_{47}^{\text{down}} = 1,\ P_{44}^{\text{left}} = 1,\ P_{45}^{\text{right}} = 1 \\ &P_{52}^{\text{up}} = 1,\ P_{58}^{\text{down}} = 1,\ P_{54}^{\text{left}} = 1,\ P_{56}^{\text{right}} = 1 \\ &P_{63}^{\text{up}} = 1,\ P_{69}^{\text{down}} = 1,\ P_{65}^{\text{left}} = 1,\ P_{66}^{\text{right}} = 1 \\ &P_{74}^{\text{up}} = 1,\ P_{77}^{\text{down}} = 1,\ P_{77}^{\text{left}} = 1,\ P_{78}^{\text{right}} = 1 \\ &P_{85}^{\text{up}} = 1,\ P_{88}^{\text{down}} = 1,\ P_{87}^{\text{left}} = 1,\ P_{89}^{\text{right}} = 1 \\ &P_{96}^{\text{up}} = 1,\ P_{99}^{\text{down}} = 1,\ P_{98}^{\text{left}} = 1,\ P_{99}^{\text{right}} = 1 \\ \end{aligned} P19up=1, P19down=1, P19left=1, P19right=1P22up=1, P25down=1, P21left=1, P23right=1P33up=1, P36down=1, P32left=1, P33right=1P41up=1, P47down=1, P44left=1, P45right=1P52up=1, P58down=1, P54left=1, P56right=1P63up=1, P69down=1, P65left=1, P66right=1P74up=1, P77down=1, P77left=1, P78right=1P85up=1, P88down=1, P87left=1, P89right=1P96up=1, P99down=1, P98left=1, P99right=1
可得每个状态的 9 个方程式和 9 个未知数。
Vπ(1)V^\pi(1)Vπ(1) 方程是一种特殊情况,这是因为不管采取何种行为,总是转移到状态 9 且获得回报 r19a=+10r_{19}^a = +10r19a=+10。由此,可得 Vπ(1)=∑a=14(0.25)(∑9P19a(r19a+γVπ(9)))V^\pi(1) = \sum_{a=1}^4 (0.25) \left( \sum_{9} P_{19}^a \left( r_{19}^a + \gamma V^\pi(9) \right) \right) Vπ(1)=a=1∑4(0.25)(9∑P19a(r19a+γVπ(9))) 其中 ∑9P19a(r19a+γVπ(9))=r19a+0.9Vπ(9)\sum_{9} P_{19}^a \left( r_{19}^a + \gamma V^\pi(9) \right) = r_{19}^a + 0.9 V^\pi(9) 9∑P19a(r19a+γVπ(9))=r19a+0.9Vπ(9) 为便于表示,将上标置于 VπV^\piVπ,则第一个方程如下: V(1)=10+0.9V(9)V(1) = 10 + 0.9 V(9) V(1)=10+0.9V(9) 接下来,对状态 2 执行同样步骤。
V(2)=∑a=14(0.25)∑s′P2s′a(r2s′a+γv(s′))=0.25∑s′P2s′up(r2s′up+γV(s′))+0.25∑s′P2s′down(r2s′down+γV(s′))+0.25∑s′P2s′left(r2s′left+γV(s′))+0.25∑s′P2s′right(r2s′right+γV(s′))\begin{aligned} V(2) &= \sum_{a=1}^4 (0.25) \sum_{s'} P_{2s'}^a \left( r_{2s'}^a + \gamma v(s') \right) \\ &= 0.25 \sum_{s'} P_{2s'}^{\text{up}} \left( r_{2s'}^{\text{up}} + \gamma V(s') \right) + 0.25 \sum_{s'} P_{2s'}^{\text{down}} \left( r_{2s'}^{\text{down}} + \gamma V(s') \right) \\ &+ 0.25 \sum_{s'} P_{2s'}^{\text{left}} \left( r_{2s'}^{\text{left}} + \gamma V(s') \right) + 0.25 \sum_{s'} P_{2s'}^{\text{right}} \left( r_{2s'}^{\text{right}} + \gamma V(s') \right) \end{aligned} V(2)=a=1∑4(0.25)s′∑P2s′a(r2s′a+γv(s′))=0.25s′∑P2s′up(r2s′up+γV(s′))+0.25s′∑P2s′down(r2s′down+γV(s′))+0.25s′∑P2s′left(r2s′left+γV(s′))+0.25s′∑P2s′right(r2s′right+γV(s′)) 观察式中右侧的概率,可知取值为 1 或 0。例如,若考察 P2s′upP_{2s'}^{\text{up}}P2s′up 项,其只有取值为 P22up=1P_{22}^{\text{up}} = 1P22up=1,而其他状态转移为 Pup=0P^{\text{up}} = 0Pup=0。此外,若智能体试图向上移动,将会触碰边界而得到 −1-1−1 的回报。上式可重写为 V(2)=0.25(−1+0.9V(2))+0.25(0+0.9V(5))+0.25(0+0.9V(1))+0.25(0+0.9V(3))=0.225V(1)+0.225V(2)+0.225V(3)+0.225V(5)−0.25\begin{aligned} V(2) &= 0.25 \left( -1 + 0.9 V(2) \right) + 0.25 \left( 0 + 0.9 V(5) \right) + 0.25 \left( 0 + 0.9 V(1) \right) + 0.25 \left( 0 + 0.9 V(3) \right) \\ &= 0.225 V(1) + 0.225 V(2) + 0.225 V(3) + 0.225 V(5) - 0.25 \end{aligned} V(2)=0.25(−1+0.9V(2))+0.25(0+0.9V(5))+0.25(0+0.9V(1))+0.25(0+0.9V(3))=0.225V(1)+0.225V(2)+0.225V(3)+0.225V(5)−0.25 为进一步实验验证,列写 V(3)V(3)V(3) 的方程。
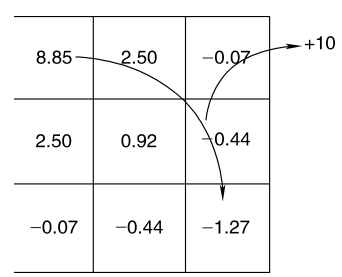
V(3)=0.25(−1+0.9V(3))+0.25(0+0.9V(6))+0.25(−1+0.9V(3))+0.25(0+0.9V(2))=0.225V(2)+0.45V(3)+0.225V(6)−0.5\begin{aligned} V(3) &= 0.25 \left( -1 + 0.9 V(3) \right) + 0.25 \left( 0 + 0.9 V(6) \right) + 0.25 \left( -1 + 0.9 V(3) \right) + 0.25 \left( 0 + 0.9 V(2) \right) \\ &= 0.225 V(2) + 0.45 V(3) + 0.225 V(6) - 0.5 \end{aligned} V(3)=0.25(−1+0.9V(3))+0.25(0+0.9V(6))+0.25(−1+0.9V(3))+0.25(0+0.9V(2))=0.225V(2)+0.45V(3)+0.225V(6)−0.5 不断执行确定每个状态下相应方程的过程,并以矩阵形式列写方程为 AV=B\mathbf{A}\mathbf{V} = \mathbf{B}AV=B,其中,矩阵 A\mathbf{A}A 如下: A=[10000000−0.9−0.2250.775−0.2250−0.22500000−0.2250.5500−0.225000−0.225000.775−0.2250−0.225000−0.2250−0.2251−0.2250−0.225000−0.2250−0.2250.77500−0.225000−0.225000.55−0.22500000−0.2250−0.2250.775−0.22500000−0.2250−0.2250.55]\mathbf{A} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -0.9 \\ -0.225 & 0.775 & -0.225 & 0 & -0.225 & 0 & 0 & 0 & 0 \\ 0 & -0.225 & 0.55 & 0 & 0 & -0.225 & 0 & 0 & 0 \\ -0.225 & 0 & 0 & 0.775 & -0.225 & 0 & -0.225 & 0 & 0 \\ 0 & -0.225 & 0 & -0.225 & 1 & -0.225 & 0 & -0.225 & 0 \\ 0 & 0 & -0.225 & 0 & -0.225 & 0.775 & 0 & 0 & -0.225 \\ 0 & 0 & 0 & -0.225 & 0 & 0 & 0.55 & -0.225 & 0 \\ 0 & 0 & 0 & 0 & -0.225 & 0 & -0.225 & 0.775 & -0.225 \\ 0 & 0 & 0 & 0 & 0 & -0.225 & 0 & -0.225 & 0.55 \\ \end{bmatrix} A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1−0.2250−0.2250000000.775−0.2250−0.22500000−0.2250.5500−0.2250000000.775−0.2250−0.225000−0.2250−0.2251−0.2250−0.225000−0.2250−0.2250.77500−0.225000−0.225000.55−0.22500000−0.2250−0.2250.775−0.225−0.90000−0.2250−0.2250.55⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ 矩阵 B\mathbf{B}B 为 BT=[10−0.25−0.5−0.250−0.25−0.5−0.25−0.5]\mathbf{B}^T = \begin{bmatrix} 10 & -0.25 & -0.5 & -0.25 & 0 & -0.25 & -0.5 & -0.25 & -0.5 \end{bmatrix} BT=[10−0.25−0.5−0.250−0.25−0.5−0.25−0.5] 求解包含 9 个方程和 9 个未知数的方程组,得到每个状态下的实际值如下: VT=[8.852.5−0.072.50.92−0.44−0.07−0.44−1.27]\mathbf{V}^T = \begin{bmatrix} 8.85 & 2.5 & -0.07 & 2.5 & 0.92 & -0.44 & -0.07 & -0.44 & -1.27 \end{bmatrix} VT=[8.852.5−0.072.50.92−0.44−0.07−0.44−1.27]
python程序如下:
import numpy as npimport matplotlib.pyplot as pltimport matplotlib.patches as patchesfrom matplotlib.animation import FuncAnimationfrom scipy.linalg import solveimport seaborn as sns# 设置中文字体plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']plt.rcParams['axes.unicode_minus'] = Falseclass GridWorld:"""3x3网格世界环境,基于文档描述的强化学习问题"""def __init__(self, grid_size=3, gamma=0.9):self.grid_size = grid_sizeself.n_states = grid_size * grid_sizeself.gamma = gamma # 折扣因子# 动作定义:0=上, 1=下, 2=左, 3=右self.actions = ['上', '下', '左', '右']self.n_actions = len(self.actions)# 每个动作的概率(均匀随机策略)self.action_prob = 0.25# 初始化状态转移矩阵和奖励矩阵self.init_transitions_and_rewards()def init_transitions_and_rewards(self):"""初始化状态转移概率和奖励函数"""# P[s][a][s'] = 从状态s采取动作a转移到状态s'的概率self.P = np.zeros((self.n_states, self.n_actions, self.n_states))# R[s][a][s'] = 从状态s采取动作a转移到状态s'的奖励self.R = np.zeros((self.n_states, self.n_actions, self.n_states))for s in range(self.n_states):for a in range(self.n_actions):s_next, reward, _ = self.get_next_state_reward(s, a)self.P[s][a][s_next] = 1.0 # 确定性转移self.R[s][a][s_next] = rewarddef state_to_pos(self, state):"""将状态编号转换为(行,列)位置"""return (state // self.grid_size, state % self.grid_size)def pos_to_state(self, row, col):"""将(行,列)位置转换为状态编号"""return row * self.grid_size + coldef get_next_state_reward(self, state, action):"""根据当前状态和动作获取下一个状态和奖励实现文档中描述的转移规则"""row, col = self.state_to_pos(state)# 特殊规则:到达状态1(左上角)立即跳转到状态9(右下角)并获得+10奖励if state == 0: # 状态1return 8, 10, True # 跳转到状态9,获得+10奖励# 根据动作计算下一个位置new_row, new_col = row, colreward = 0hit_boundary = Falseif action == 0: # 上new_row = row - 1if new_row < 0:hit_boundary = Trueelif action == 1: # 下new_row = row + 1if new_row >= self.grid_size:hit_boundary = Trueelif action == 2: # 左new_col = col - 1if new_col < 0:hit_boundary = Trueelif action == 3: # 右new_col = col + 1if new_col >= self.grid_size:hit_boundary = True# 如果碰到边界,停留在原位并给予-1惩罚if hit_boundary:return state, -1, Falseelse:next_state = self.pos_to_state(new_row, new_col)return next_state, 0, Falsedef compute_value_function(self):"""计算价值函数 V^π(s)求解线性方程组 A*V = B"""n = self.n_statesA = np.zeros((n, n))B = np.zeros(n)for s in range(n):# 对角线元素:1 - γ * Σ_a π(a|s) * P(s'|s,a) * [s'==s]A[s][s] = 1.0for a in range(self.n_actions):for s_next in range(n):if self.P[s][a][s_next] > 0:# 期望奖励B[s] += self.action_prob * self.P[s][a][s_next] * self.R[s][a][s_next]# 转移概率项if s_next != s:A[s][s_next] -= self.action_prob * self.gamma * self.P[s][a][s_next]else:A[s][s] -= self.action_prob * self.gamma * self.P[s][a][s_next]# 求解线性方程组V = solve(A, B)return Vdef simulate_episode(self, start_state, max_steps=100):"""模拟一个episode,记录智能体的移动轨迹"""trajectory = [start_state]current_state = start_statetotal_reward = 0for _ in range(max_steps):# 随机选择动作action = np.random.choice(self.n_actions)next_state, reward, _ = self.get_next_state_reward(current_state, action)trajectory.append(next_state)total_reward += rewardcurrent_state = next_state# 如果到达状态9,可以结束(或者继续模拟)if current_state == 8: # 状态9breakreturn trajectory, total_rewarddef visualize_grid(self, V=None, trajectory=None, save_path=None):"""可视化网格环境、价值函数和轨迹"""fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))# 左图:网格环境ax1.set_title('网格世界环境', fontsize=14, fontweight='bold')ax1.set_xlim(-0.5, self.grid_size - 0.5)ax1.set_ylim(-0.5, self.grid_size - 0.5)ax1.set_aspect('equal')ax1.grid(True, alpha=0.3)ax1.set_xticks(range(self.grid_size))ax1.set_yticks(range(self.grid_size))ax1.set_xlabel('列')ax1.set_ylabel('行')# 绘制网格和标注for i in range(self.grid_size):for j in range(self.grid_size):state = self.pos_to_state(i, j)# 根据状态类型设置颜色if state == 0: # 状态1 - 特殊起点color = 'lightgreen'label = '状态1\n(→9,+10)'elif state == 8: # 状态9 - 目标color = 'lightcoral'label = '状态9'else:color = 'lightblue'label = f'状态{state+1}'rect = patches.Rectangle((j-0.4, i-0.4), 0.8, 0.8,linewidth=2, edgecolor='black',facecolor=color, alpha=0.7)ax1.add_patch(rect)ax1.text(j, i, label, ha='center', va='center',fontsize=10, fontweight='bold')# 如果有轨迹,绘制轨迹if trajectory:for i in range(len(trajectory)-1):curr_pos = self.state_to_pos(trajectory[i])next_pos = self.state_to_pos(trajectory[i+1])ax1.annotate('', xy=(next_pos[1], next_pos[0]),xytext=(curr_pos[1], curr_pos[0]),arrowprops=dict(arrowstyle='->', color='red', lw=2))# 标记起点和终点start_pos = self.state_to_pos(trajectory[0])end_pos = self.state_to_pos(trajectory[-1])ax1.plot(start_pos[1], start_pos[0], 'go', markersize=12, label='起点')ax1.plot(end_pos[1], end_pos[0], 'ro', markersize=12, label='终点')ax1.legend()# 右图:价值函数热力图if V is not None:V_grid = V.reshape((self.grid_size, self.grid_size))sns.heatmap(V_grid, annot=True, fmt='.2f', cmap='RdYlBu_r',center=0, square=True, ax=ax2,xticklabels=range(1, self.grid_size+1),yticklabels=range(1, self.grid_size+1))ax2.set_title('状态价值函数 V(s)', fontsize=14, fontweight='bold')ax2.set_xlabel('列')ax2.set_ylabel('行')# 标注特殊状态ax2.text(0.5, 0.5, '→9', ha='center', va='center',fontsize=8, fontweight='bold', color='darkgreen')ax2.text(2.5, 2.5, '目标', ha='center', va='center',fontsize=8, fontweight='bold', color='darkred')plt.tight_layout()if save_path:plt.savefig(save_path, dpi=300, bbox_inches='tight')plt.show()def visualize_learning_process(self, n_episodes=1000):"""可视化学习过程中价值函数的收敛"""# 使用迭代方法计算价值函数(动态规划)V_history = []V = np.zeros(self.n_states)for episode in range(n_episodes):V_new = np.zeros(self.n_states)for s in range(self.n_states):value = 0for a in range(self.n_actions):for s_next in range(self.n_states):if self.P[s][a][s_next] > 0:value += (self.action_prob * self.P[s][a][s_next] *(self.R[s][a][s_next] + self.gamma * V[s_next]))V_new[s] = valueV = V_new.copy()V_history.append(V.copy())# 每100个episode记录一次if episode % 100 == 0:print(f"Episode {episode}: V = {V}")return np.array(V_history)def main():"""主函数:演示网格世界环境"""print("=" * 60)print("3×3网格世界强化学习环境")print("=" * 60)# 创建网格世界环境env = GridWorld(grid_size=3, gamma=0.9)print("\n环境参数:")print(f"- 网格大小:{env.grid_size}×{env.grid_size}")print(f"- 状态数量:{env.n_states}")print(f"- 动作空间:{env.actions}")print(f"- 折扣因子:{env.gamma}")print(f"- 策略:均匀随机(每个动作概率={env.action_prob})")# 计算价值函数print("\n正在计算价值函数...")V = env.compute_value_function()print("\n各状态的价值函数 V(s):")print("-" * 40)for i in range(env.n_states):pos = env.state_to_pos(i)print(f"状态{i+1} 位置{pos}: V = {V[i]:.4f}")# 验证与文档结果对比expected_V = np.array([8.85, 2.5, -0.07, 2.5, 0.92, -0.44, -0.07, -0.44, -1.27])print("\n与文档结果对比:")print("-" * 40)for i in range(env.n_states):diff = abs(V[i] - expected_V[i])print(f"状态{i+1}: 计算={V[i]:.4f}, 期望={expected_V[i]:.4f}, 误差={diff:.4f}")print(f"\n平均绝对误差: {np.mean(np.abs(V - expected_V)):.4f}")# 模拟多个episodeprint("\n模拟智能体移动轨迹:")print("-" * 40)for start in [0, 4, 8]: # 从不同起点开始trajectory, total_reward = env.simulate_episode(start, max_steps=20)print(f"\n从状态{start+1}开始的轨迹:")print(f"轨迹: {' → '.join([str(s+1) for s in trajectory])}")print(f"总奖励: {total_reward}")print(f"步数: {len(trajectory)-1}")# 可视化print("\n正在生成可视化图表...")# 1. 可视化网格环境和价值函数env.visualize_grid(V=V, save_path='grid_world_value.png')# 2. 可视化一个示例轨迹trajectory, _ = env.simulate_episode(start_state=0, max_steps=10)env.visualize_grid(V=V, trajectory=trajectory, save_path='grid_world_trajectory.png')print("\n可视化图表已保存!")# 3. 学习过程可视化print("\n正在计算学习过程...")V_history = env.visualize_learning_process(n_episodes=500)# 绘制收敛过程plt.figure(figsize=(12, 8))for i in range(env.n_states):plt.plot(V_history[:, i], label=f'状态{i+1}', alpha=0.7)plt.xlabel('迭代次数')plt.ylabel('价值函数 V(s)')plt.title('价值函数收敛过程')plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')plt.grid(True, alpha=0.3)plt.tight_layout()plt.savefig('value_convergence.png', dpi=300, bbox_inches='tight')plt.show()print("\n收敛图已保存为 'value_convergence.png'")return env, Vif __name__ == "__main__":env, V = main()
============================================================
3×3网格世界强化学习环境
============================================================环境参数:
- 网格大小:3×3
- 状态数量:9
- 动作空间:['上', '下', '左', '右']
- 折扣因子:0.9
- 策略:均匀随机(每个动作概率=0.25)正在计算价值函数...各状态的价值函数 V(s):
----------------------------------------
状态1 位置(0, 0): V = 8.8547
状态2 位置(0, 1): V = 2.4959
状态3 位置(0, 2): V = -0.0698
状态4 位置(1, 0): V = 2.4959
状态5 位置(1, 1): V = 0.9232
状态6 位置(1, 2): V = -0.4443
状态7 位置(2, 0): V = -0.0698
状态8 位置(2, 1): V = -0.4443
状态9 位置(2, 2): V = -1.2726与文档结果对比:
----------------------------------------
状态1: 计算=8.8547, 期望=8.8500, 误差=0.0047
状态2: 计算=2.4959, 期望=2.5000, 误差=0.0041
状态3: 计算=-0.0698, 期望=-0.0700, 误差=0.0002
状态4: 计算=2.4959, 期望=2.5000, 误差=0.0041
状态5: 计算=0.9232, 期望=0.9200, 误差=0.0032
状态6: 计算=-0.4443, 期望=-0.4400, 误差=0.0043
状态7: 计算=-0.0698, 期望=-0.0700, 误差=0.0002
状态8: 计算=-0.4443, 期望=-0.4400, 误差=0.0043
状态9: 计算=-1.2726, 期望=-1.2700, 误差=0.0026平均绝对误差: 0.0031模拟智能体移动轨迹:
----------------------------------------从状态1开始的轨迹:
轨迹: 1 → 9
总奖励: 10
步数: 1从状态5开始的轨迹:
轨迹: 5 → 8 → 9
总奖励: 0
步数: 2从状态9开始的轨迹:
轨迹: 9 → 8 → 5 → 8 → 5 → 8 → 7 → 7 → 4 → 4 → 4 → 1 → 9
总奖励: 7
步数: 12正在生成可视化图表...可视化图表已保存!正在计算学习过程...
Episode 0: V = [10. -0.25 -0.5 -0.25 0. -0.25 -0.5 -0.25 -0.5 ]
Episode 100: V = [ 8.85467727 2.49590905 -0.06978246 2.49590905 0.92324015 -0.44426238-0.06978246 -0.44426238 -1.27257986]
Episode 200: V = [ 8.85468581 2.49591758 -0.06977392 2.49591758 0.92324868 -0.44425384-0.06977392 -0.44425384 -1.27257132]
Episode 300: V = [ 8.85468581 2.49591759 -0.06977392 2.49591759 0.92324869 -0.44425384-0.06977392 -0.44425384 -1.27257132]
Episode 400: V = [ 8.85468581 2.49591759 -0.06977392 2.49591759 0.92324869 -0.44425384-0.06977392 -0.44425384 -1.27257132]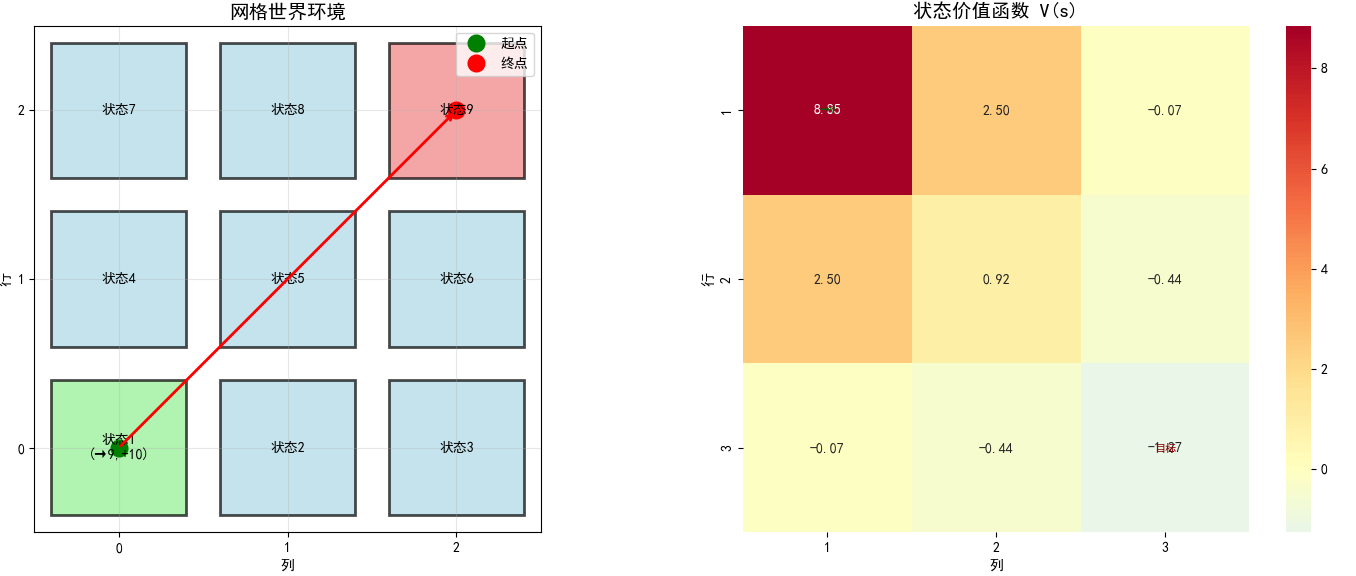
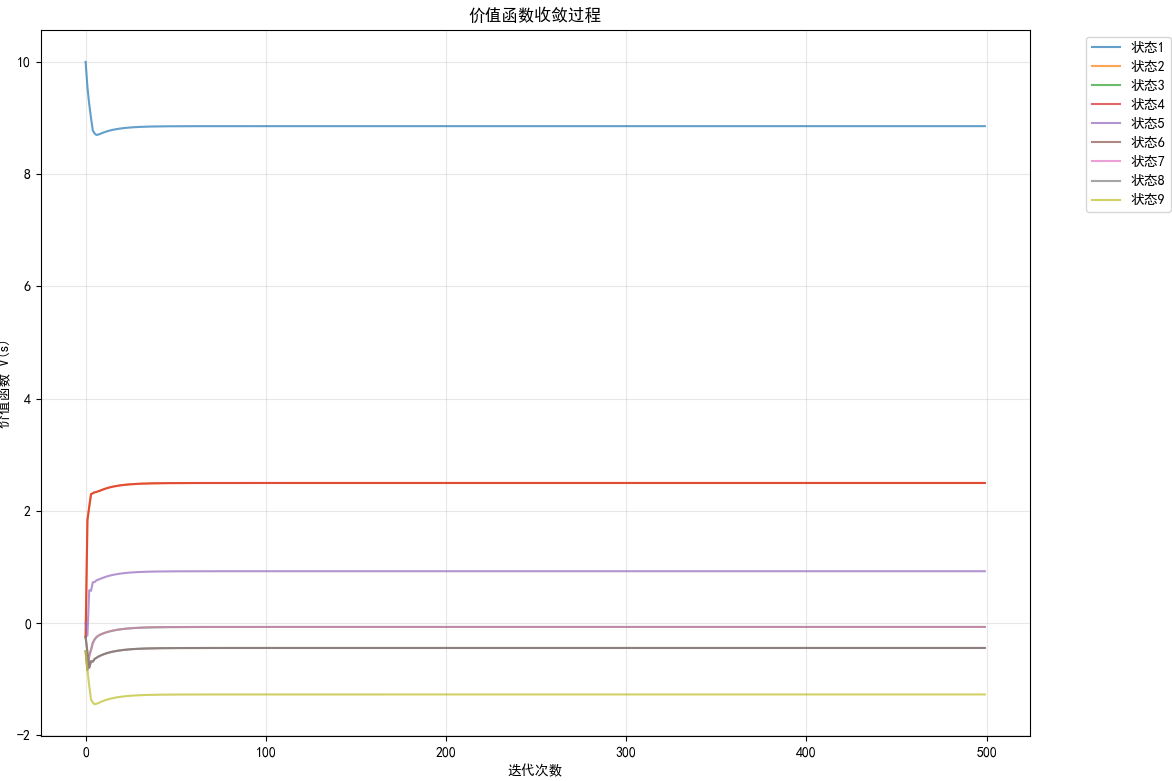
2.6 MDP
可参照2.随机性-强化学习笔记2_强化学习中,为什么下一个状态是随机的-CSDN博客
2.7 学习值函数
值函数迭代算法
初始化V(s)=0V(s)=0V(s)=0,对于所有的s∈Ss\in Ss∈S
重复
设Δ=0\Delta=0Δ=0
对于每个s∈Ss\in Ss∈S:
v←V(s)v\gets V(s)v←V(s)
V(s)→∑aπ(s,a)∑a′Pss′a(Rss′a+γVk(s′))V(s)\to\sum_{a}\pi(s,a)\sum_{a'}P^a_{ss'}(R^a_{ss'}+\gamma V_k(s'))V(s)→∑aπ(s,a)∑a′Pss′a(Rss′a+γVk(s′))
Δ=max(Δ,∣v−V(s)∣)\Delta=max(\Delta,|v-V(s)|)Δ=max(Δ,∣v−V(s)∣)
直到Δ<θ\Delta<\thetaΔ<θ,对于所有s∈Ss\in Ss∈S (θ\thetaθ为一个小的正数)
这可给出每个状态下值的初始假设值。注意,必须事先已知策略π(s,a)\pi(s,a)π(s,a)、状态转移概率P(s′∣s,a)P(s'|s,a)P(s′∣s,a)和奖励函数R(s,a,s′)R(s,a,s')R(s,a,s′),然后计算差值Δ=Vk+1−Vk\Delta = V_{k+1} - V_kΔ=Vk+1−Vk。一旦这个差值足够小,则立刻停止递归。
2.8 策略迭代
2.7讲的是如何在已知策略π(s,a)\pi(s,a)π(s,a)、状态转移概率P(s′∣s,a)P(s'|s,a)P(s′∣s,a)和奖励函数R(s,a,s′)R(s,a,s')R(s,a,s′)的情况下得出最优的状态值。
但是如何确定是否一个能够提供更大回报的更好的策略呢?
算法2.2 策略迭代算法
- 初始化 V(s)=0V(s) = 0V(s)=0,对于所有 s∈Ss \in Ss∈S
- 策略评价
- 重复
- Δ=0\Delta = 0Δ=0
- 对于每个 s∈Ss \in Ss∈S:
- v←V(s)v \leftarrow V(s)v←V(s)
- V(s)←∑aπ(s,a)∑s′Pss′a(Rss′a+γVk(s′))V(s) \leftarrow \sum_a \pi(s, a) \sum_{s'} P_{ss'}^a \left( R_{ss'}^a + \gamma V_k(s') \right)V(s)←∑aπ(s,a)∑s′Pss′a(Rss′a+γVk(s′))
- Δ=max(Δ,∣v−V(s)∣)\Delta = \max(\Delta, |v - V(s)|)Δ=max(Δ,∣v−V(s)∣)
- 直到 Δ<θ\Delta < \thetaΔ<θ,对于所有 s∈Ss \in Ss∈S(θ\thetaθ 为一个小的正数)
- 策略改进
- 重复
- 对于每个 s∈Ss \in Ss∈S:
- b←π(s)b \leftarrow \pi(s)b←π(s)
- π(s)←maxa∑s′Pss′a(Rss′a+γVk(s′))\pi(s) \leftarrow \max_a \sum_{s'} P_{ss'}^a \left( R_{ss'}^a + \gamma V_k(s') \right)π(s)←maxa∑s′Pss′a(Rss′a+γVk(s′))
- 若 b≠π(s)b \neq \pi(s)b=π(s),则返回到策略评价
- 直到 b≠π(s)b \neq \pi(s)b=π(s)
上述算法包含两个阶段
- 第一阶段, 根据值迭代算法计算每个状态的值
- 第二阶段, 最优动作价值函数搜索最大化行为
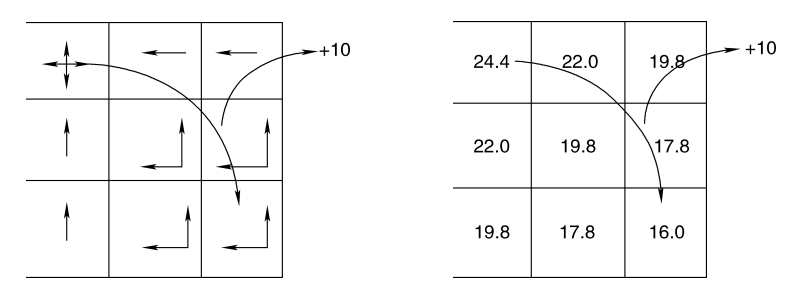
上图为求得的最优策略
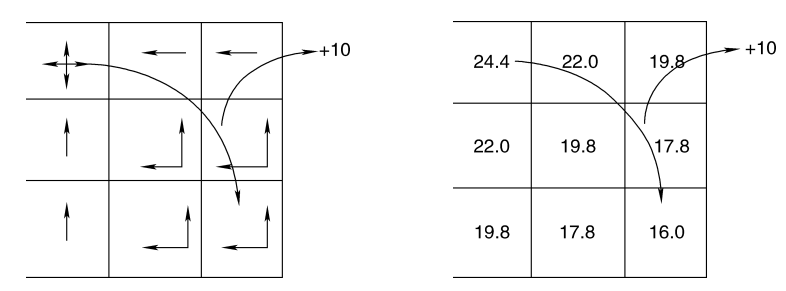
上图为基于最优策略求得的状态值
2.9 时间差分学习
可参考深度学习(6)Sarsa算法-CSDN博客
解决转移概率Pss′aP^a_{ss'}Pss′a和回报Raa′aR^a_{aa'}Raa′a均未知的情况。
首先从每个状态的值函数的初始值估计开始,在实际应用中,通常将值函数初始化为0.
定义:
ϵ=rt+1+γV(s′)−V(s)\epsilon=r_{t+1}+\gamma V(s')-V(s)ϵ=rt+1+γV(s′)−V(s)
然后更新状态值的估计:
Vk+1(s)=Vk(s)+α[rt+1+γV(s′)−V(s)]V_{k+1}(s)=V_k(s)+\alpha[r_{t+1}+\gamma V(s')-V(s)]Vk+1(s)=Vk(s)+α[rt+1+γV(s′)−V(s)]
算法 时间差分算法
-
- 初始化V(s)=0V(s)=0V(s)=0,对于所有ϵ∈S\epsilon \in Sϵ∈S
- 2.初始化sss为任意值
- 3.重复
- 4.对于每个步长时刻:
- 根据策略π(s)\pi(s)π(s)选择行为aaa
- 得到回报rrr和下一个状态s′s's′
- V(s)←V(s)+α(r+γV(s′)−V(S))V(s) \gets V(s) + \alpha(r+\gamma V(s')-V(S))V(s)←V(s)+α(r+γV(s′)−V(S))
- s=s′s=s's=s′
- 5.直到完成所需步长或者s到达终止状态
2.10 状态-行为函数的时间差分学习
本节将采用 ϵ\epsilonϵ- 贪婪行为选择过程
Qk+1(st,at)=Qk(st,at)+α[rt+1+γQk(st+1,at+1−Qk(st,at)]Q_{k+1}(s_t,a_t)= Q_k(s_t,a_t)+\alpha[r_{t+1}+\gamma Q_k(s_{t+1},a_{t+1}-Q_k(s_t,a_t)]Qk+1(st,at)=Qk(st,at)+α[rt+1+γQk(st+1,at+1−Qk(st,at)]
首先,将Q表中的值初始化为随机数,在网格示例中,Q表为一个9×4的表。通过贪婪迭代,最终得出下表。
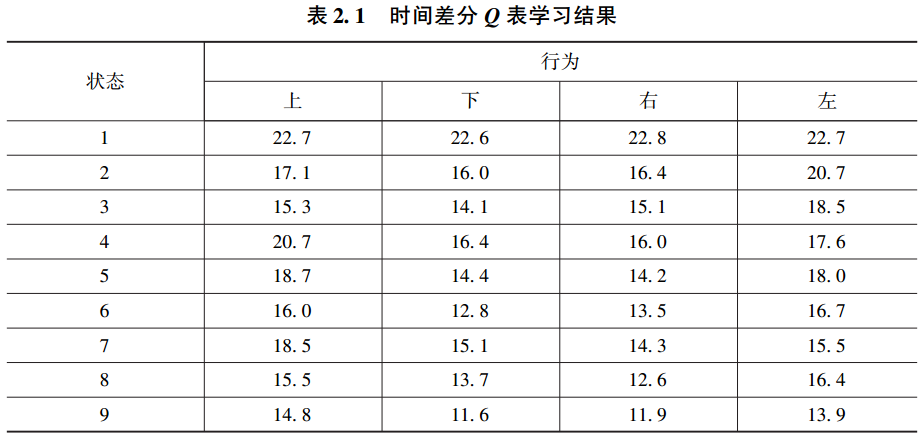
算法 时间差分状态 - 行为算法
- 初始化 Q(s,a)Q(s,a)Q(s,a) 为任意值(随机数)
- 初始化状态 sss 为任意值
- 根据 εεε 贪婪策略来选择行为 aaa
- 重复
- 执行行为 a 并转移到下一状态 sss′,得到回报 rrr
- 利用 $ε $贪婪策略来选择状态 s′s′s′ 处的下一行为 a′a′a′
- Q(s,a)←Q(s,a)+α[r+γQ(s′,a′)−Q(s,a)]Q(s,a)←Q(s,a)+α[r+γQ(s′,a′)−Q(s,a)]Q(s,a)←Q(s,a)+α[r+γQ(s′,a′)−Q(s,a)]
- 设 a=a′,s=s′a=a′,s=s′a=a′,s=s′
- 直到完成特定步长数或sss 达到终止状态
2.11 Q学习
强化学习(4) DQN及其编程实现_dqn策略的实现编写-CSDN博客
2.12 资格迹
上述算法中的时间差分学习都可以看作一步预测:
xk+1=xk+α[rt+1+γy(t+1)−y(t)]⏟仅取决于最后时间步的结果x_{k+1}=x_{k}+\alpha\underbrace{[r_{t+1}+\gamma y(t+1)-y(t)]}_{仅取决于最后时间步的结果}xk+1=xk+α仅取决于最后时间步的结果[rt+1+γy(t+1)−y(t)]
在资格迹的情况下, 将及时进一步回顾总结。 例如, 如果当前回报较好, 则不仅更新当前状态, 并为导致到达该状态的某些先前状态分配一些回报。 这将会大大提高算法的收敛时间。
根据折扣未来回报来定义回报如下:
Rt=rt+1+γrt+2+γ2rt+3+⋯+γT−t−1=rt+1+Vt(st+1)R_t=r_{t+1}+\gamma r_{t+2}+ \gamma^2r_{t+3}+\cdots+\gamma^{T-t-1}=r_{t+1}+V_t(s_{t+1})Rt=rt+1+γrt+2+γ2rt+3+⋯+γT−t−1=rt+1+Vt(st+1)
则两部预测的形式为:
Rt=rt+1+γrt+2+γ2Vt(st+2)R_t=r_{t+1}+\gamma r_{t+2}+\gamma^2V_t(s_{t+2})Rt=rt+1+γrt+2+γ2Vt(st+2)
资格迹法会跟踪上次访问特定状态的轨迹, 然后将当前回报分配给最近访问的状态。 而长时间没有被访问的状态则没有资格获得当前回报.
定义时刻 t 每个状态的资格迹为 et(s)e_t(s)et(s) 。 每个状态的资格迹以 γαγαγα 速率衰减,且对于刚访问过的状态, 其资格迹会增大 1 。 因此, 更新资格迹如下:
et(s)={γλet−1(s)如果 s≠stγλet−1(s)+1如果 s=ste_t(s) = \begin{cases} \gamma \lambda e_{t-1}(s) & \text{如果 } s \neq s_t \\ \gamma \lambda e_{t-1}(s) + 1 & \text{如果 } s = s_t \end{cases}et(s)={γλet−1(s)γλet−1(s)+1如果 s=st如果 s=st
一步预测误差为
δt=rr+1+γVt(St+1)−Vt(st)\delta_t=r_{r+1}+\gamma V_t(S_{t+1})-V_t(s_t)δt=rr+1+γVt(St+1)−Vt(st)
每个状态的校正为:
ΔVt(s)=αδtet(s)∀s\Delta V_t(s)=\alpha \delta_t e_t(s)\forall sΔVt(s)=αδtet(s)∀s
