相向双指针|两数之和II-输入有序数组|三数之和|统计和小于目标的下标对数目|最接近的三数之和|四数之和|有效三角形的个数

相向双指针，最重要的就是【数组】+【递增排序】
两数之和用一个循环while
三数之和用两个循环for+while

167.两数之和II-输入有序数组

两数之和II-输入有序数组

思路

数组给咱们的是排序好的，所有不用sort函数了。那自然而然定义两根指针，一个在数组头l，一个在数组尾r

这样定义的好处是

两根指针中间的数字一定比头指针要大，一定比尾指针要小

如果两指针之和大于target的话，那中间某个数加上尾指针肯定也比target要大，那说明两个数加起来大了，那就把右边大的数字减小一点

如果两指针之和小于target的话，那头指针加上中间某个数肯定也比target要小，那说明两个数加起来小了，那就把左边大的数字增大一点

如果两指针之和等于target的话，那说明我们找到了答案直接返回就行

代码

class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int l=0,r=numbers.size()-1;while(l<r){if(numbers[l]+numbers[r]>target)r--;else if(numbers[l]+numbers[r]<target)l++;elsereturn {l+1,r+1};}return {};//理论上是不会进行到这一步的，但是为了保证所有的路劲都有返回值。}
};

碰到的问题

1. twoSum是solution类提供的一个函数方法。我们可以创建实例去调用它。
2. 函数接口中用的是vector<int>& numbers，这样就不会发生拷贝构造函数了。
3. if/else if/else 写成if/ if/else 会发生严重错误的
4. 保证每个路径都有返回值。

15.三数之和

15. 三数之和

思路：

跟着上一题的思路走。上一次是nums[l]和nums[r]和target比大小

nums[l]+nums[r]=target 

这一题只不过是转换为了

nums[l]+nums[r]+nums[i] = 0
nums[l]+nums[r]= -nums[i]

所以依旧可以用我们的相向双指针
那么只需要在上一题的代码上加一层循环，循环i就完事了

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> res;sort(nums.begin(),nums.end());for(int i=0;i<nums.size()-2;i++){int l=i+1,r=nums.size()-1;while(l<r){if(nums[l]+nums[r]+nums[i]>0)r--;else if(nums[l]+nums[r]+nums[i]<0)l++;else{res.push_back({nums[i],nums[l],nums[r]});l++;r--;}}}return res;}
};

这是跟着上一题的思路可以写到的地方

去重

1. 对i去重

if(i&&nums[i]==nums[i-1])continue;

就是i在大于0时，如果和上一个i值一样的话那就直接跳过

2. 对l和r进行优化

while(l<r&&nums[l]==nums[l-1]) l++;
while(l<r&&nums[r]==nums[r+1]) r--;

对l和r和 对i的操作是一样的

完整代码：

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> res;sort(nums.begin(),nums.end());for(int i=0;i<nums.size()-2;i++){int l=i+1,r=nums.size()-1;if(i&&nums[i]==nums[i-1])continue;while(l<r){if(nums[l]+nums[r]+nums[i]>0)r--;else if(nums[l]+nums[r]+nums[i]<0)l++;else{res.push_back({nums[i],nums[l],nums[r]});l++;r--;while(l<r&&nums[l]==nums[l-1]) l++;while(l<r&&nums[r]==nums[r+1]) r--;}}}return res;}
};

碰到的问题

1. vector的方法push_back()
2. 搞忘记快排了。

2824.统计和小于目标的下标对数目

2824. 统计和小于目标的下标对数目
nums[i] + nums[j] < target

思路

1. 和两数之和思路一样，大了就r–，小了就收集答案。
2. 再加一点小巧思在里面。

代码

class Solution {
public:int countPairs(vector<int>& nums, int target) {sort(nums.begin() , nums.end());int count = 0;int l = 0;int r = nums.size() - 1;while(l<r){if(nums[l]+nums[r] >= target)r--;else{count+=r-l;l++;}}return count;}
};

16.最接近的三数之和

16. 最接近的三数之和
选出三个整数，使它们的和与 target 最接近。

思路

1. 与三数之和很像
2. 再加一个min_diff=INT_MAX.来记录三数之和和target之间的最小差值。作最接近的设计

代码

class Solution {
public:int threeSumClosest(vector<int>& nums, int target) {sort(nums.begin() , nums.end());int res=0;int min_diff = INT_MAX;for (int i = 0; i < nums.size() - 2;i++){int l = i + 1;int r = nums.size() - 1;while(l<r){int cur = nums[i] + nums[l] + nums[r];if( cur > target){if(cur -target <min_diff){min_diff = cur - target;res = cur;}r--;}else if( cur < target){if(target - cur <min_diff){min_diff = target - cur;res = cur;}l++;}elsereturn cur;}}return res;}
};

18.四数之和

18. 四数之和
nums[a] + nums[b] + nums[c] + nums[d] == target

思路

1. 就是在三数之和上再套一个循环
2. 去重。

//第一层i的去重if(i&&nums[i]==nums[i-1])   continue;//第二层j的去重if (j>i+1&&nums[j]==nums[j-1]) continue;//第三层l，r的去重while(l<r&&nums[l]==nums[l-1];l++);while(l<r&&nums[r]==nums[r+1];r--);

代码

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> res;if(nums.size()<4)return res;sort(nums.begin(),nums.end());for(int i=0;i<nums.size()-3;i++){long long a=nums[i];if(i&&nums[i]==nums[i-1])   continue;for(int j=i+1;j<nums.size()-2;j++){if (j>i+1&&nums[j]==nums[j-1]) continue; // 跳过重复数字int l=j+1,r=nums.size()-1;while(l<r){long long x=a+nums[j]+nums[l]+nums[r];if(x>target)r--;else if(x<target)l++;else{res.push_back({nums[i],nums[j],nums[l],nums[r]});for(l++;l<r&&nums[l]==nums[l-1];l++);for(r--;l<r&&nums[r]==nums[r+1];r--);}}}}return res;}
};

碰到的问题

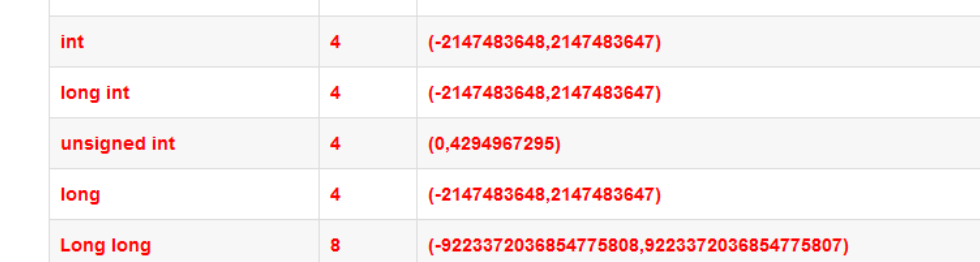
1. int型数据是2.1*10^9,当四数相加时就要用long long了。（这个就是大数运算，碰到大数时一定要用long long）
   

611.有效三角形的个数

思路

1. 三数之和的基础
2. 但固定的i是在最右边，依次变小。（以前是在最左边）
3. 如果i在最左边依次变大，会导致相向双指针有二义性，这个方法就失效了。如2 2 3 4.i在最左边，固定i时，l=2，r=4.（num【i】+num【l】=num【r】）此时到底是右移L，还是左移R，不管移动谁，都会漏值。

代码

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int res = 0;for (int i = nums.size()-1; i > 1;i--){int l = 0;int r = i-1;while(l<r){if(nums[l]+nums[r] >nums[i]){res += (r - l);r--;}elsel++;}}return res;}
};