LeetCode 3143.正方形中的最多点数

给你一个二维数组 points 和一个字符串 s ，其中 points[i] 表示第 i 个点的坐标，s[i] 表示第 i 个点的 标签 。

如果一个正方形的中心在 (0, 0) ，所有边都平行于坐标轴，且正方形内 不 存在标签相同的两个点，那么我们称这个正方形是 合法 的。

请你返回 合法 正方形中可以包含的 最多 点数。

注意：

如果一个点位于正方形的边上或者在边以内，则认为该点位于正方形内。
正方形的边长可以为零。

示例 1：

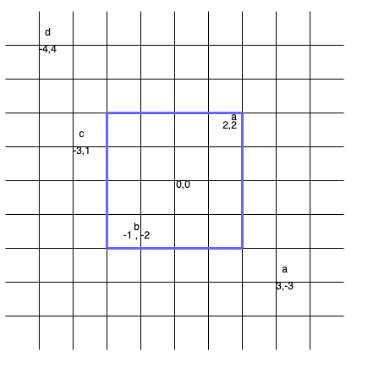
输入：points = [[2,2],[-1,-2],[-4,4],[-3,1],[3,-3]], s = “abdca”

输出：2

解释：

边长为 4 的正方形包含两个点 points[0] 和 points[1] 。

示例 2：

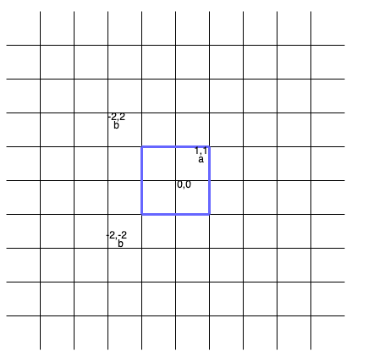
输入：points = [[1,1],[-2,-2],[-2,2]], s = “abb”

输出：1

解释：

边长为 2 的正方形包含 1 个点 points[0] 。

示例 3：

输入：points = [[1,1],[-1,-1],[2,-2]], s = “ccd”

输出：0

解释：

任何正方形都无法只包含 points[0] 和 points[1] 中的一个点，所以合法正方形中都不包含任何点。

提示：

1 <= s.length, points.length <= 10${}^5$
points[i].length == 2
-10${}^9$ <= points[i][0], points[i][1] <= 10${}^9$
s.length == points.length
points 中的点坐标互不相同。
s 只包含小写英文字母。

我们可以二分正方形的二分之一边长，二分下界是0，二分上界是离远点最远的点的坐标(x,y)中，abs(x)和abs(y)较大的那个：

class Solution {
public:int maxPointsInsideSquare(vector<vector<int>>& points, string s) {vector<int> &maxP = *max_element(points.begin(), points.end(), [] (vector<int> point1, vector<int> point2) {return max(abs(point1[0]), abs(point1[1])) < max(abs(point2[0]), abs(point2[1]));});int l = 0;int r = max(abs(maxP[0]), abs(maxP[1]));int ans = 0;while (l <= r) {int m = l + (r - l) / 2;int pointNum = 0;set<char> charSet;bool invalid = false;for (int i = 0; i < points.size(); ++i) {vector<int> &point = points[i];if (max(abs(point[0]), abs(point[1])) <= m) {if (charSet.find(s[i]) != charSet.end()) {invalid = true;break;}++pointNum;charSet.insert(s[i]);}}if (invalid) {r = m - 1;} else {ans = pointNum;l = m + 1;}}return ans;}
};

如果points的长度为n，s中字符的种类为m，二分上下界为l，则此算法时间复杂度为O(nlogl)，空间复杂度为O(m)。