LeetCode——二分(进阶)

相关例题
852. 山脉数组的峰顶索引
题目描述
给定一个长度为 n 的整数 山脉 数组 arr ,其中的值递增到一个 峰值元素 然后递减。
返回峰值元素的下标。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
示例 1:
输入:arr = [0,1,0]
输出:1
示例 2:
输入:arr = [0,2,1,0]
输出:1
示例 3:
输入:arr = [0,10,5,2]
输出:1
提示:
3 <= arr.length <= 1050 <= arr[i] <= 106- 题目数据 保证
arr是一个山脉数组
题目分析
这类题目如果之前没做过的话还是不容易想到用二分的,实际上是这个题目是可以使用二分的思想来解决的,因为我们的这个数组还是有一定的二段性的规律的,比如我们可以通过题意知道我们的峰值的左边都是当前值大于左值的,而我们的峰值右边则是当前值要小于我们的右值的,我们的峰值则是大于了两侧的值,这样我们就有了二分的区间选择。图示:
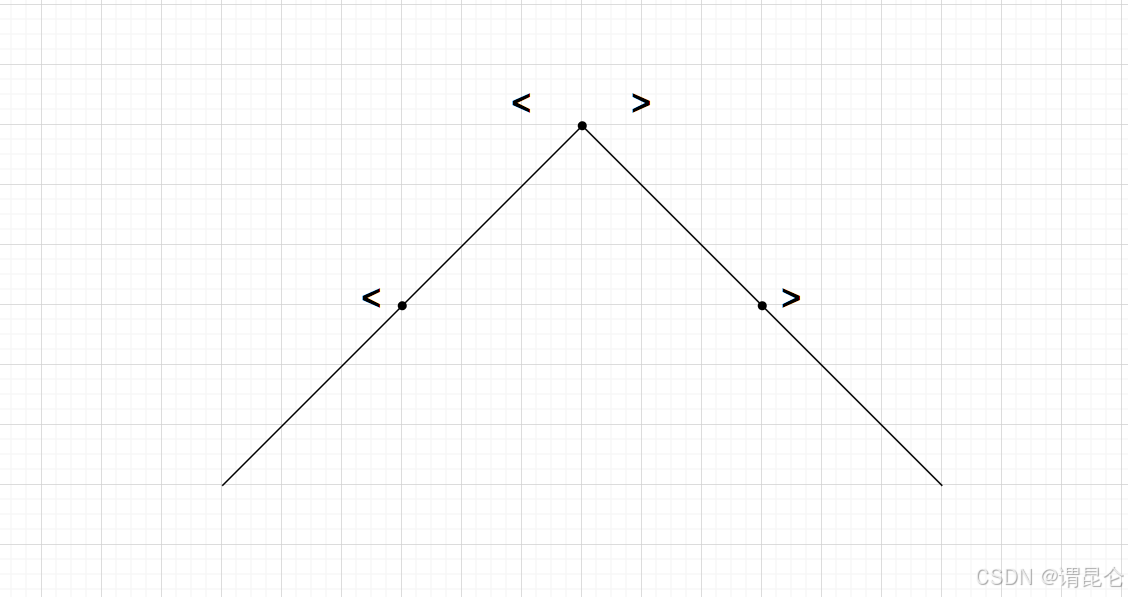
实现思路
这里我们也是有了两种情况:
1、当我们的当前值是大于左值的时候,说明在左边,这个时候我们需要我们需要将left置为mid(这里的mid可能就是答案)。
2、当我们的当前值是小于等于右值的时候,说明在右边,这个时候我们需要将right置为mid - 1。
然后就是返回我们的结果。
实现代码
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 1, right = arr.size() - 2;while(left < right) {int mid = left + (right - left + 1) / 2;if(arr[mid] > arr[mid - 1]) left = mid;else right = mid - 1;}return left;}
};
寻找峰值
题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
题目分析
其实这个题目和上面这个题目是一模一样的思路和解法,我们这里可以找出题目中的二段性进行分析就可以发现出这个题目和上面的题目一模一样。
实现思路
我们这里还是来寻找一下题目中的二段性,我们这里可以取出任意一个点i,那么对于i和i + 1就有了两种情况了:
当我们的arr[i] > arr[i + 1]的时候,这个时候当前值的左侧一定会有山峰(最左侧是负无穷)。
当我们的arr[i] < arr[i + 1]的时候,这个时候当前值的右侧一定会有山峰(最右侧是负无穷)。
实现代码
class Solution {
public:int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]>nums[mid-1]) left=mid;else right=mid-1;}return left;}
};
寻找旋转排序数组中的最小值
题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
题目分析
这个题目其实也是可以使用二分解决的,关键在于找出二段性,我们可以从题意中知道,我们旋转之后的数组实际上是一种局部递增的机构,总共有两种情形:
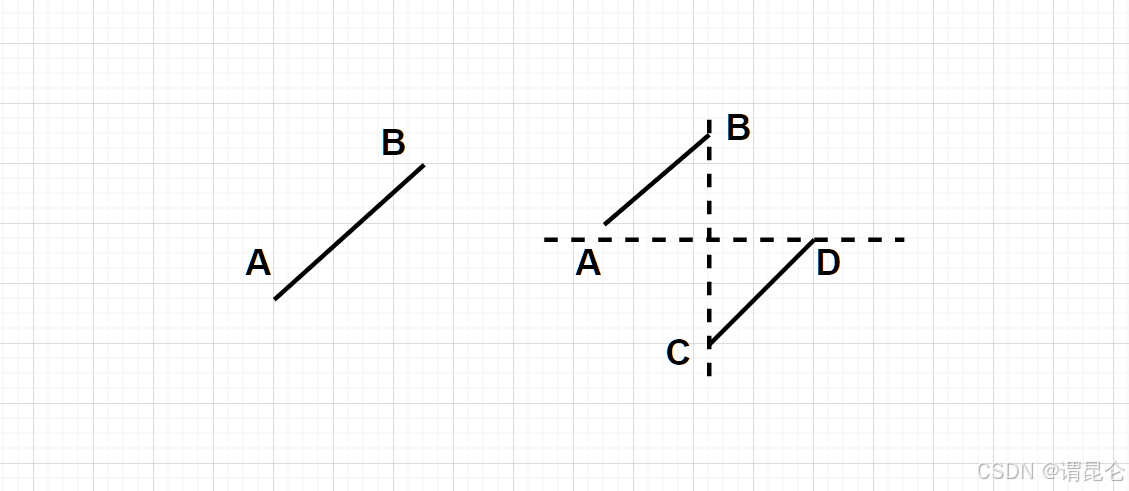
我们这里其实可以直接看成是第二种情形,我们这里从图中也是可以知道的我们的D点可以将数组分成两块,一部分是[A, B]这里的值是大于D的,一部分是[C, D]这里部分是小于等于D的,这就是我们的二段性,于是我们可以将D作为指标进行二分操作。
实现思路
首先我们需要定义出两个指针,一个指向了数组的最左端,一个指向了数组的最右端,并且还要标记一下我们的最后位置。
然后就是我们的二分模板了,条件处理:
当我们的mid对应的值要大于最后一个值时,我们的left = mid + 1,说明目标在右边。
当我们的mid对应的值是小于等于我们的最后一个值的时候,我们的right = mid,说明我们的目标在包含当前值的左边。
实现代码
class Solution {
public:int findMin(vector<int>& nums) {int left = 0, right = nums.size() - 1;int x = nums[right]; while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > x)left = mid + 1;elseright = mid;}return nums[left];}
};
点名
题目描述
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入:records = [0,1,2,3,5]
输出:4
示例 2:
输入:records = [0, 1, 2, 3, 4, 5, 6, 8]
输出:7
提示:
1 <= records.length <= 10000
题目分析
这个题目其实也是可以使用二分来解决的,我们这里重要的还是寻找出我们的二段性,这里从题目中我们不难发现我们的二段性就是我的当前值的下标和当前值是不是相等的。
实现思路
定义两个指针,一个指针指向数组的开头,一个指向了数组的结尾。
进入二分模板中的循环,这里主要是讨论两种情况:
1、当我的当前值和我们的下标是相等的时候,说明包括当前值的左边都是合法的,left = mid + 1。
2、当我的当前值和我们的下标是不相等的时候,说明包括当前值和我们的右边都是不合法的,right = mid。
这里重点还是细节问题,我们需要返回的right,也就是开始不符合位置的下标,但是有可能我们的数组都是符合的,也就是说我们要的值是最后一个值的下一位,这里需要进行特判。
实现代码
class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0, right = records.size() - 1;while (left < right) {int mid = left + (right - left) / 2;if (records[mid] == mid)left = mid + 1;elseright = mid;}return right == records[right] ? right + 1 : right;}
};
注意:这里的返回值也可以是left。
