数据结构——二十八、图的基本操作(王道408)

前言

本文总结了图的两种常见存储方式（邻接矩阵和邻接表）及其基本操作实现。首先介绍了图的12种基本操作，包括判断边是否存在、查找邻接边、插入/删除顶点和边等。重点分析了邻接矩阵和邻接表的初始化方法，给出了C语言定义和辅助函数实现。针对"判断边是否存在"和"查找邻接边"两个核心操作，分别从时间复杂度（邻接矩阵O(1)，邻接表O(V)）和代码实现进行了详细说明，并配以图示说明。最后还区分了无向图和有向图的不同处理方式。这些内容为考研数据结构中图的重点考察内容。

代码文件在文章开头,需要自取🧐
考研中最常考的还是邻接矩阵和邻接表

一.总览基本操作

• Adjacent(G,x,y): 判断图G是否存在边<x,y>或(x,y).
• Neighbors(G,x): 列出图G中与结点x邻接的边。
• InsertVertex(G,x): 在图G中插入顶点x.
• DeleteVertex(G,x): 从图G中删除顶点x.
• AddEdge(G,x,y): 若无向边(x,y)或有向边<x,y>不存在，则向图G中添加该边。
• RemoveEdge(G,x,y): 若无向边(x,y)或有向边<x,y>存在，则从图G中删除该边。
• FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1.
• NextNeighbor(G,x,y): 假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1.
• Get_edge_value(G,x,y): 获取图G中边(x,y)或<x,y>y>对应的权值。
• Set_edge_value(G,x,y,v): 设置图G中边(x,y)或<x,y>对应的权值为v.

1.初始化

1.邻接矩阵

1.定义

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>#define MAX_VERTEX_NUM 100
#define INFINITY INT_MAXtypedef char VertexType;
typedef int EdgeType;// 邻接矩阵存储的图
typedef struct {VertexType vexs[MAX_VERTEX_NUM];          // 顶点数组EdgeType edges[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵int vexnum, arcnum;                       // 顶点数和边数
} MGraph;

2.初始化与辅助函数

// 初始化图
void InitMGraph(MGraph *G) {G->vexnum = 0;G->arcnum = 0;for (int i = 0; i < MAX_VERTEX_NUM; i++) {for (int j = 0; j < MAX_VERTEX_NUM; j++) {G->edges[i][j] = (i == j) ? 0 : INFINITY;}}
}
// 查找顶点位置
int LocateVex(MGraph *G, VertexType v) {for (int i = 0; i < G->vexnum; i++) {if (G->vexs[i] == v) {return i;}}return -1;
}

2.邻接表

1.定义

// 邻接表存储的图
typedef struct ArcNode {int adjvex;              // 该边指向的顶点位置struct ArcNode *next;    // 指向下一条边的指针EdgeType info;           // 边权值
} ArcNode;typedef struct VNode {VertexType data;         // 顶点信息ArcNode *first;          // 指向第一条边的指针
} VNode, AdjList[MAX_VERTEX_NUM];typedef struct {AdjList vertices;        // 邻接表int vexnum, arcnum;      // 顶点数和边数
} ALGraph;

2.初始化与辅助函数

// 初始化邻接表
void InitALGraph(ALGraph *G) {G->vexnum = 0;G->arcnum = 0;for (int i = 0; i < MAX_VERTEX_NUM; i++) {G->vertices[i].first = NULL;}
}// 查找顶点位置
int LocateVexAL(ALGraph *G, VertexType v) {for (int i = 0; i < G->vexnum; i++) {if (G->vertices[i].data == v) {return i;}}return -1;
}

二.判断图是否存在指定边

Adjacent(G,x,y)：判断图G是否存在边<x，y>或(x，y)。

1.邻接矩阵

有向图与无向图都是这个思路

1.思路

• 比如说要判断B和D之间是否有边,那我们只需要找到B和D所对应的这个元素,判断它是否为1
• 如果为1,就说明存在,为0则说明不存在

2.时间复杂度

• O(1)

3.代码

// 判断边是否存在
int Adjacent(MGraph *G, VertexType x, VertexType y) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return 0;return (G->edges[i][j] != INFINITY && G->edges[i][j] != 0);
}

2.邻接表

有向图与无向图都是这个思路

1.思路

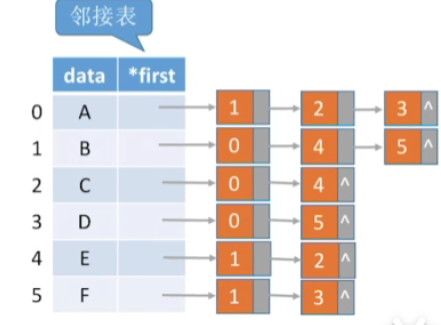
• 比如判断B和D之间是否有边,那么我们可以检查B的这个边结点到底有没有D,也就是有没有3

2.时间复杂度

• 最好的情况是我们要找的那个目标节点所对应的编号,刚好就是第一个元素,时间复杂度O(1)
• 而最坏的情况是你遍历完整个B的所有边节点,结果都没有发现我们要找的这个节点,而和B连接的边最多有可能有|V|-1条,O|V|

3.代码

// 判断边是否存在
int AdjacentAL(ALGraph *G, VertexType x, VertexType y) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return 0;ArcNode *p = G->vertices[i].first;while (p != NULL) {if (p->adjvex == j) {return 1;}p = p->next;}return 0;
}

三.列出图当中和指定节点相邻接的所有的边

Neighbors(G,x)：列出图G中与结点x邻接的边。

1.邻接矩阵

1.存储无向图

1.思路

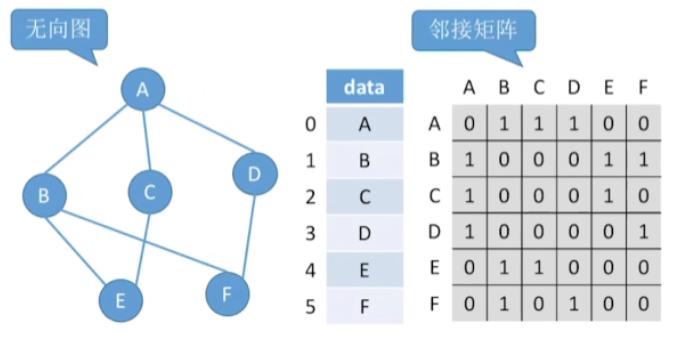
• 只需要便利和它所对应的矩阵当中的这一行或者这一列
• 然后检查哪些地方元素是1把这些元素所对应的边给列举出来

2.时间复杂度

• O(|V|)

3.代码

// 列出邻接边
void Neighbors(MGraph *G, VertexType x) {int i = LocateVex(G, x);if (i == -1) return;printf("顶点 %c 的邻接边: ", x);for (int j = 0; j < G->vexnum; j++) {if (G->edges[i][j] != INFINITY && G->edges[i][j] != 0) {printf("(%c,%c) ", x, G->vexs[j]);}}printf("\n");
}

2.存储有向图

1.思路

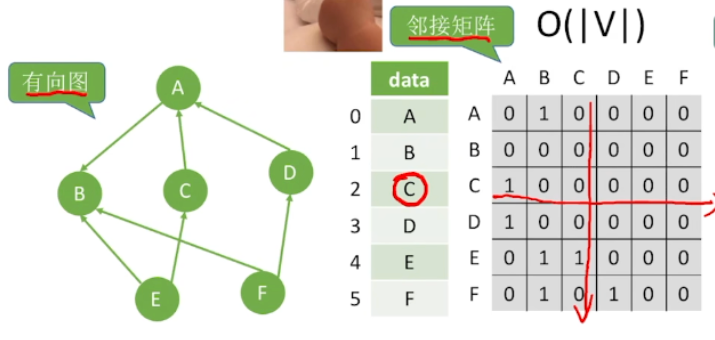
• 只需要便利和它对应的这一整行找到出边,要再便利和它所对应的这一列找到出边

2.时间复杂度

• 时间复杂度也是O(|V|)

2.邻接表

1.存储无向图

1.思路

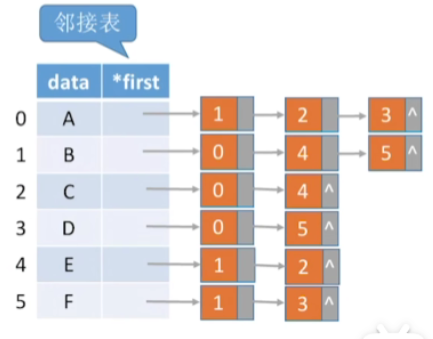
• 只需要遍历和它相连的这个边节点的链表就可以

2.时间复杂度

• 那最好的情况是当前这个节点只连了一个边,时间复杂度O(1)
• 最坏的情况就是当前这个节点上边连了尽可能多的边,时间复杂度O(|V|)

3.代码

// 列出邻接边
void NeighborsAL(ALGraph *G, VertexType x) {int i = LocateVexAL(G, x);if (i == -1) return;printf("顶点 %c 的邻接边: ", x);ArcNode *p = G->vertices[i].first;while (p != NULL) {printf("(%c,%c) ", x, G->vertices[p->adjvex].data);p = p->next;}printf("\n");
}

2.存储有向图

1.思路

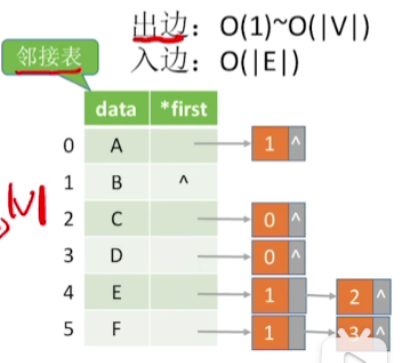
• 找出边和之前的一样,只需要遍历和它相连的这一整个边的链表就可以
• 而如果要找指向当前这个节点的入边的话,那是不是我们就得遍历整个连接表所有的这些边结点
• 因为只有便利完所有的这些边结点,才可以确定到底有几条边是指向C这个节点的

2.时间复杂度

• 出边时间复杂度:O(1)~O(|V|)
• 入边时间复杂度:O(|E|)

适合稀疏图

四.在图中插入新顶点

InsertVertex(G,x):在图G中插入顶点x

1.邻接矩阵

有向图与无向图都是这个思路

1.思路

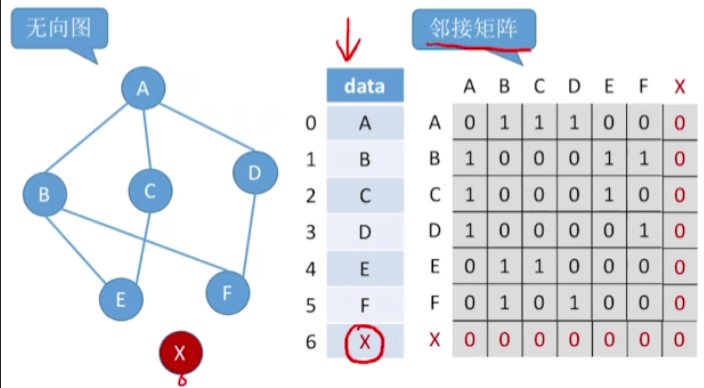
• 刚开始插入这个顶点的时候,这个顶点和其他的任何顶点都是不相连的,所以其实插入是很方便的
• 只需要在保存这些顶点的这个数组的后面空白的位置,写入新节点的一个数据
• 那在邻接矩阵当中,与新元素相对应的这一行和这一列,就可以表现当前这个新元素和其他顶点的一个连接关系

2.时间复杂度

• 看起来我们似乎要在矩阵当中插入这么多个0元素,但是其实矩阵的这些元素化0,这件事情应该是在你的邻接矩阵被初始化的时候就已经做好了,所以其实插入新顶点的唯一开销就是写入这个顶点相关的信息,因此可以在O(1)这样的时间复杂度完成

3.代码

int InsertVertex(MGraph *G, VertexType x) {if (G->vexnum >= MAX_VERTEX_NUM) return 0;if (LocateVex(G, x) != -1) return 0; // 顶点已存在G->vexs[G->vexnum] = x;G->vexnum++;return 1;
}

2.邻接表

有向图与无向图都是这个思路

1.思路

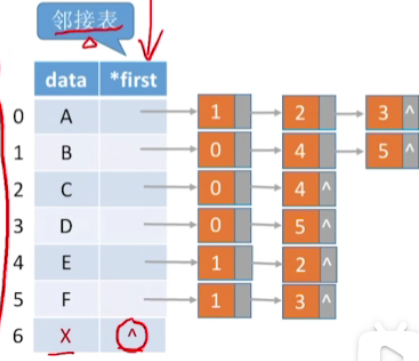
• 只需要在存储节点的这个数组的末尾,插入新节点的信息就可以
• 新结点指针设置为NULL

2.时间复杂度

• 时间复杂度:O(1)

3.代码

// 插入顶点
int InsertVertexAL(ALGraph *G, VertexType x) {if (G->vexnum >= MAX_VERTEX_NUM) return 0;if (LocateVexAL(G, x) != -1) return 0; // 顶点已存在G->vertices[G->vexnum].data = x;G->vertices[G->vexnum].first = NULL;G->vexnum++;return 1;
}

五.从图中删除指定顶点

DeleteVertex(G,x):从图G中删除顶点x。

1.邻接矩阵

有向图和无向图删除方法一样

1.思路

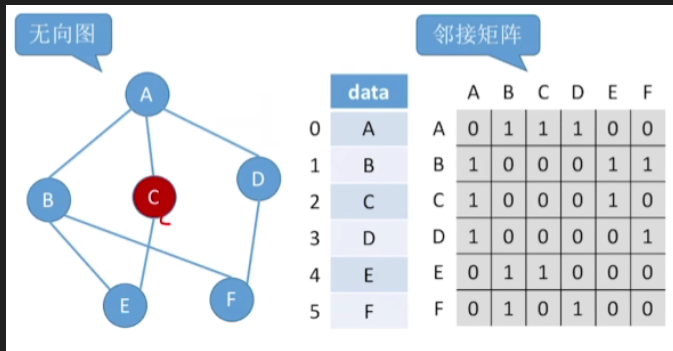
• 比如说我们要删除的是C这个顶点

• 删除C之后是不是相当于我们要把和它对应的这一行这一列,所有的这些数据都清空

• 清空这些数据之后一个比较容易想到的方法是我们可以让后续的这些数据都依次前移

• 那对于邻接矩阵来说,就是要把我们删除的这个十字周围的这些元素都让它们再拼接起来
  

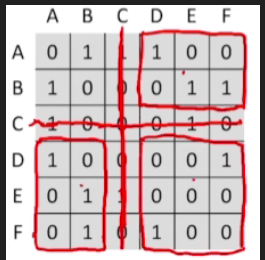
• 但是如果这么操作的话,那就意味着会有大量的数据元素需要移动

• 那么当我们删除一个顶点之后,其实我们只需要把和这个顶点相对应的这一行,还有这一列全部变成零就可以了

• 然后我们可以在顶点的结构体当中增加一个布尔型的变量,用于表示这个顶点是否是一个空顶点

2.时间复杂度

• O(|V|)

3.代码

// 删除顶点
int DeleteVertex(MGraph *G, VertexType x) {int pos = LocateVex(G, x);if (pos == -1) return 0;// 统计要删除的边数int deleted_edges = 0;for (int i = 0; i < G->vexnum; i++) {if (G->edges[pos][i] != INFINITY && G->edges[pos][i] != 0) deleted_edges++;if (G->edges[i][pos] != INFINITY && G->edges[i][pos] != 0) deleted_edges++;}// 删除顶点for (int i = pos; i < G->vexnum - 1; i++) {G->vexs[i] = G->vexs[i + 1];}// 删除相关的行和列for (int i = pos; i < G->vexnum - 1; i++) {for (int j = 0; j < G->vexnum; j++) {G->edges[i][j] = G->edges[i + 1][j];}}for (int j = pos; j < G->vexnum - 1; j++) {for (int i = 0; i < G->vexnum; i++) {G->edges[i][j] = G->edges[i][j + 1];}}G->vexnum--;G->arcnum -= deleted_edges / 2; // 无向图每条边被统计两次return 1;
}

2.邻接表

1.存储无向图

1.思路

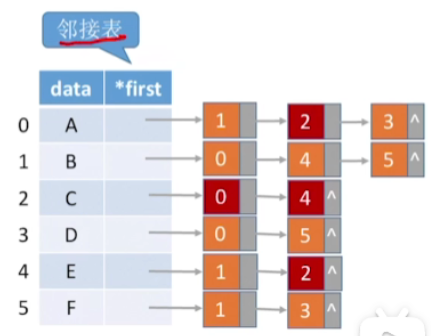
• 要删除C这个顶点
• 那我们除了删除C还有和它相连的这些边结点之外,我们还需要在其他和它相连的这些顶点的边表当中,找到指向C这个节点的这些边的信息,也把这些信息给删除
  

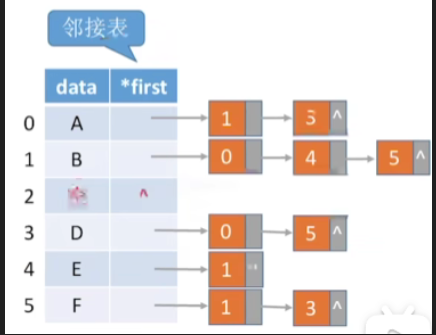
2.时间复杂度

• 那连接表的删除操作最好的情况当然是当前删除的节点,它原本就没有连任何边
• 那这种情况只需要O(1)的时间复杂度就可以完成
• 而最坏的情况是当前删除的这个顶点,它后边连了尽可能多的边,也就是它和其他所有的顶点都有相连的边,那么在删除当前节点的边表之后,是不是还需要去依次便利和它相连的其他这些顶点的边表
• 这种情况下最坏的情况是,2号顶点相连的这条边的信息都是接在最后一个位置,就意味着我们需要遍历所有这些边的信息,才可以依次地把这些该删的东西给删完
• 所以最坏的情况我们需要O(E)这样的时间复杂度

3.代码

// 删除顶点
int DeleteVertexAL(ALGraph *G, VertexType x) {int pos = LocateVexAL(G, x);if (pos == -1) return 0;// 删除以该顶点为起点的边ArcNode *p = G->vertices[pos].first;while (p != NULL) {ArcNode *temp = p;p = p->next;free(temp);G->arcnum--;}// 删除以该顶点为终点的边for (int i = 0; i < G->vexnum; i++) {if (i == pos) continue;ArcNode *prev = NULL;ArcNode *curr = G->vertices[i].first;while (curr != NULL) {if (curr->adjvex == pos) {if (prev == NULL) {G->vertices[i].first = curr->next;} else {prev->next = curr->next;}ArcNode *temp = curr;curr = curr->next;free(temp);G->arcnum--;} else {if (curr->adjvex > pos) {curr->adjvex--; // 调整顶点索引}prev = curr;curr = curr->next;}}}// 移动顶点数组for (int i = pos; i < G->vexnum - 1; i++) {G->vertices[i] = G->vertices[i + 1];// 调整边表中的顶点索引ArcNode *p = G->vertices[i].first;while (p != NULL) {if (p->adjvex > pos) {p->adjvex--;}p = p->next;}}G->vexnum--;return 1;
}

2.存储有向图

1.思路

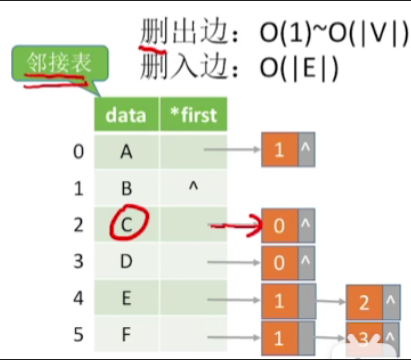
• 要删除从当前节点往外发射的这些边(出边)很方便,只需要把它的后边连的这整个链表给删除就可以
• 而如果要删除指向当前这个顶点的边(入边),那我们就只能遍历整个邻接表,把所有的这些边界点都给遍历一遍

2.时间复杂度

• 删出边：O(1)~O(|V|)
• 删入边：O(|E|)

适合稀疏图

六.在图中的指定顶点间增加一条边

AddEdge(G,x,y)：若无向边(x,y)或有向边<x,y>不存在，则向图G中添加该边。

1.邻接矩阵

有向图与无向图类似

1.思路

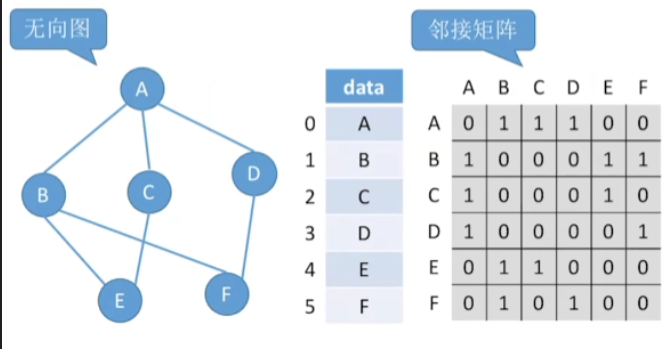
• 在对应的两个顶点之间将0变成1
• 如果本来是1则不变

2.时间复杂度

• O(1)

3.代码

// 添加边
int AddEdge(MGraph *G, VertexType x, VertexType y, EdgeType weight) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return 0;if (G->edges[i][j] == INFINITY) {G->edges[i][j] = weight;G->edges[j][i] = weight; // 无向图G->arcnum++;return 1;}return 0;
}

// 删除边
int RemoveEdge(MGraph *G, VertexType x, VertexType y) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return 0;if (G->edges[i][j] != INFINITY) {G->edges[i][j] = INFINITY;G->edges[j][i] = INFINITY; // 无向图G->arcnum--;return 1;}return 0;
}

2.邻接表

有向图与无向图类似

1.思路

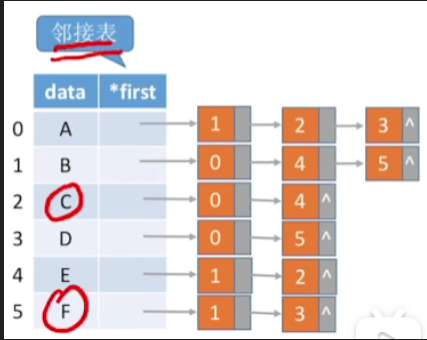
• 比如我们要添加C和F之间的一条边,那我们是不是需要在C和F边节点的链表后面头插入两个相应的顶点

2.时间复杂度

• 时间复杂度O(1)

3.代码

// 添加边
int AddEdgeAL(ALGraph *G, VertexType x, VertexType y, EdgeType weight) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return 0;// 检查边是否已存在ArcNode *p = G->vertices[i].first;while (p != NULL) {if (p->adjvex == j) {return 0; // 边已存在}p = p->next;}// 添加边 (i->j)ArcNode *newArc = (ArcNode *)malloc(sizeof(ArcNode));newArc->adjvex = j;newArc->info = weight;newArc->next = G->vertices[i].first;G->vertices[i].first = newArc;// 添加边 (j->i) - 无向图newArc = (ArcNode *)malloc(sizeof(ArcNode));newArc->adjvex = i;newArc->info = weight;newArc->next = G->vertices[j].first;G->vertices[j].first = newArc;G->arcnum++;return 1;
}

// 删除边
int RemoveEdgeAL(ALGraph *G, VertexType x, VertexType y) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return 0;int removed = 0;// 删除边 (i->j)ArcNode *prev = NULL;ArcNode *curr = G->vertices[i].first;while (curr != NULL) {if (curr->adjvex == j) {if (prev == NULL) {G->vertices[i].first = curr->next;} else {prev->next = curr->next;}free(curr);removed = 1;break;}prev = curr;curr = curr->next;}// 删除边 (j->i)prev = NULL;curr = G->vertices[j].first;while (curr != NULL) {if (curr->adjvex == i) {if (prev == NULL) {G->vertices[j].first = curr->next;} else {prev->next = curr->next;}free(curr);removed = 1;break;}prev = curr;curr = curr->next;}if (removed) {G->arcnum--;}return removed;
}

七.求图中指定顶点的第一个邻接点

FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1.

1.邻接矩阵

1.存储无向图

1.思路

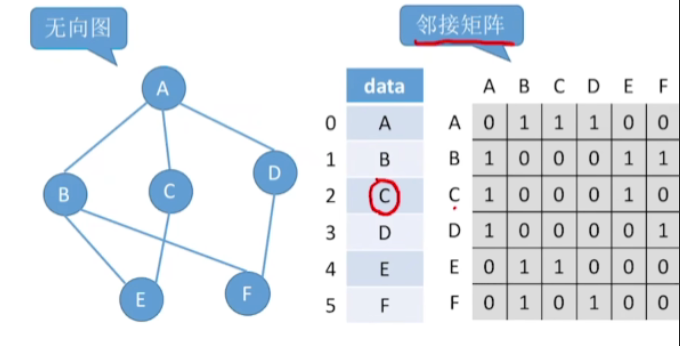
• 只需要扫描和这个顶点对应的这一行,从左到右扫描,扫描找到第一个1,那这样的话就找到了和当前节点邻接的第一个点

2.时间复杂度

• 所以最好的情况就像C节点这样,扫描到第一个元素就直接找到了,时间复杂度O(1)
• 而最坏的情况是你扫描完一整行,然后都没有发现和它相邻接的顶点,那这种情况需要O(|V|)的时间

3.代码

// 第一个邻接点
int FirstNeighbor(MGraph *G, VertexType x) {int i = LocateVex(G, x);if (i == -1) return -1;for (int j = 0; j < G->vexnum; j++) {if (G->edges[i][j] != INFINITY && G->edges[i][j] != 0) {return j;}}return -1;
}

2.存储有向图

1.思路

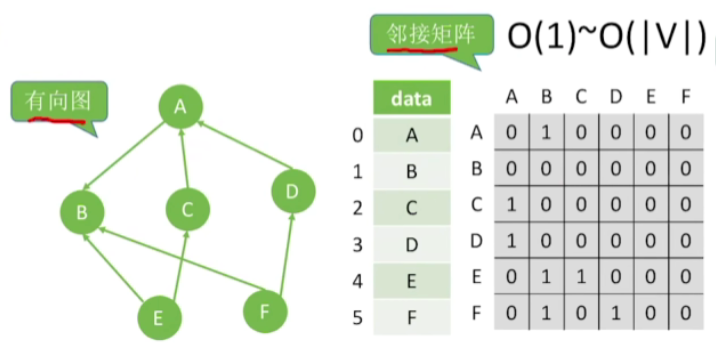
• 在邻接矩阵当中找到某一个顶点的出边,就需要扫描它的行,找入边需要扫描它的列
• 先找出边再找入边,先找到的元素就是第一个邻接点

2.时间复杂度

• O(1)~O(|V|)

2.邻接表

1.存储无向图

1.思路

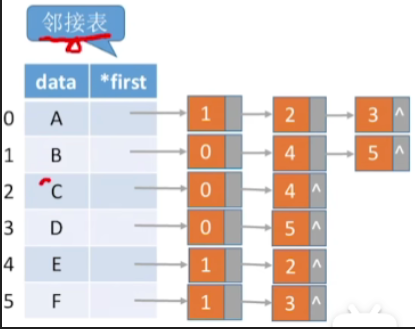
• 只需要找到他的边节点的链表当中的第一个节点

2.时间复杂度

• O(1)

3.代码

// 第一个邻接点
int FirstNeighborAL(ALGraph *G, VertexType x) {int i = LocateVexAL(G, x);if (i == -1) return -1;if (G->vertices[i].first != NULL) {return G->vertices[i].first->adjvex;}return -1;
}

2.存储有向图

1.思路

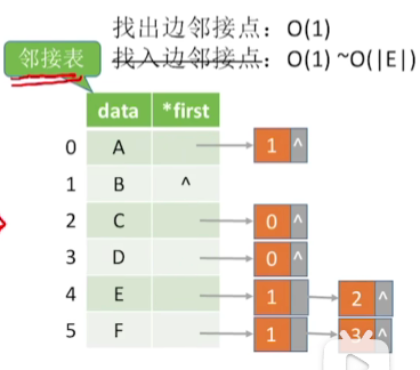
• 找出边是很方便的
• 但是找入边就比较麻烦

2.时间复杂度

• 找出边邻接点：O(1)
• 找入边邻接点：O(1)~O(|E|)(不常用)

八.找到指定顶点的除第一个邻接点的后一个邻接点

NextNeighbor(G,x,y)：假设图G中顶点x是顶点x的一个邻接点，返回除x之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1。

1.邻接矩阵

1.无边图

1.思路

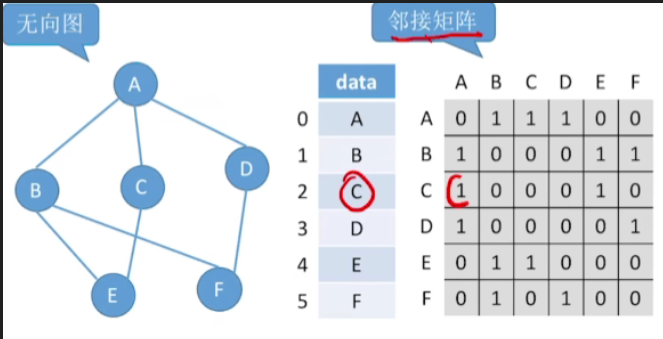
• 要找到一个邻接点之后的下一个连接点,只需要继续往后扫描就可以

2.时间复杂度

• O(1)~O(|V|)

3.代码

// 下一个邻接点
int NextNeighbor(MGraph *G, VertexType x, VertexType y) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return -1;for (int k = j + 1; k < G->vexnum; k++) {if (G->edges[i][k] != INFINITY && G->edges[i][k] != 0) {return k;}}return -1;
}

2.邻接表

1.无边图

1.思路

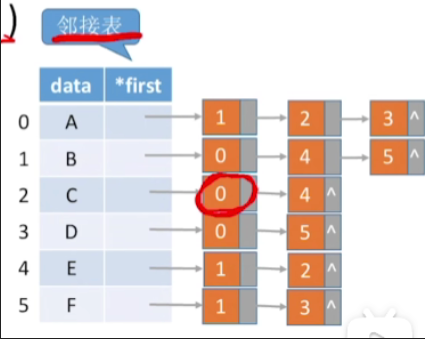
• 已知一个顶点的信息,那是不是再往后找一位就可以

2.时间复杂度

• O(1)

3.代码

// 下一个邻接点
int NextNeighborAL(ALGraph *G, VertexType x, VertexType y) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return -1;ArcNode *p = G->vertices[i].first;while (p != NULL && p->adjvex != j) {p = p->next;}if (p != NULL && p->next != NULL) {return p->next->adjvex;}return -1;
}

九.获取/设置图中指定边的权值

Get edge _ value(G,x,y)：获取图G中边(x,y)或<x，y>对应的权值。
Set edge _ value(G,x,y,v)：设置图G中边(x,y)或<x，y>对应的权值为v。

与Adjacent(G,x,y)：判断图G是否存在边<x，y>或(x，y)。雷同，核心在于找到边,因此不再赘述

1.代码

1.邻接矩阵

// 获取边权值
EdgeType Get_edge_value(MGraph *G, VertexType x, VertexType y) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return INFINITY;return G->edges[i][j];
}// 设置边权值
int Set_edge_value(MGraph *G, VertexType x, VertexType y, EdgeType v) {int i = LocateVex(G, x);int j = LocateVex(G, y);if (i == -1 || j == -1) return 0;G->edges[i][j] = v;G->edges[j][i] = v; // 无向图return 1;
}

2.邻接表

// 获取边权值
EdgeType Get_edge_valueAL(ALGraph *G, VertexType x, VertexType y) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return INFINITY;ArcNode *p = G->vertices[i].first;while (p != NULL) {if (p->adjvex == j) {return p->info;}p = p->next;}return INFINITY;
}// 设置边权值
int Set_edge_valueAL(ALGraph *G, VertexType x, VertexType y, EdgeType v) {int i = LocateVexAL(G, x);int j = LocateVexAL(G, y);if (i == -1 || j == -1) return 0;// 设置边 (i->j) 的权值ArcNode *p = G->vertices[i].first;while (p != NULL) {if (p->adjvex == j) {p->info = v;break;}p = p->next;}// 设置边 (j->i) 的权值p = G->vertices[j].first;while (p != NULL) {if (p->adjvex == i) {p->info = v;return 1;}p = p->next;}return 0;
}

十.知识回顾与重要考点

在图的遍历中能用到函数代码是标黄的函数,比较重要

结语

这章量大管饱☺️

如果想查看更多章节,请点击:一、数据结构专栏导航页