【代码随想录算法训练营——Day44】动态规划——1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列

LeetCode题目链接
https://leetcode.cn/problems/longest-common-subsequence/description/
https://leetcode.cn/problems/uncrossed-lines/description/
https://leetcode.cn/problems/maximum-subarray/description/
https://leetcode.cn/problems/is-subsequence/description/

题解
1143.最长公共子序列
代码部分带“#”的是有疑问的地方，也是看了题解的地方。这一题在写之前前一天看过题解，知道dp数组的定义是dp[i][j]为[0, i-1]和[0, j-1]长度的字符串的公共子序列的长度，也知道递推公式中有一句是dp[i][j] = dp[i - 1][j - 1] + 1，但这之外的分支就不知道怎么写了，其实是dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。

1035.不相交的线
思考了3分钟，没想清楚递推公式。

这一个是思维转换，把直线不能相交转换成有相对顺序的子序列。所以和上一题一样。

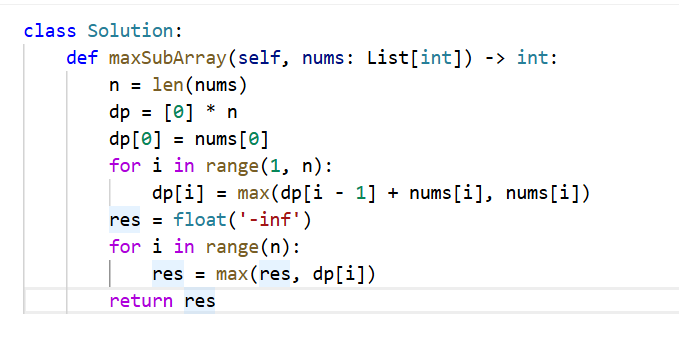
53.最大子序和
因为之前听过卡哥这题的视频讲解，利用上了印象，选定一维dp，递推公式也写对了一半，另一半是因为dp要从当前位置从头开始计数，所以要取两者之间的最大值。还有就是初始化只dp[0]即可。还有最后结果取全部值的最大值，不是最后一个。

392.判断子序列
想到暴力方法，双指针遍历。题解说是编辑距离，不是很懂。偷看到了dp数组的定义，是二维，并且也是和1143.最长公共子序列同一个定义。递推公式感觉也是一样的，只是最后需要判断最长公共子序列的长度是否和s字符串s的长度相等。

递推公式要变化。

代码

#1143.最长公共子序列
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:n, m = len(text1), len(text2)dp = [[0] * (m + 1) for _ in range(n + 1)]#base casefor i in range(1, n + 1):for j in range(1, m + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:#dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[n][m]

#1035.不相交的线
#略

#53.最大子序和

#392.判断子序列