Leetcode+Java+图论II
110.字符串迁移
题目描述
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
1. 序列中第一个字符串是 beginStr。
2. 序列中最后一个字符串是 endStr。
3. 每次转换只能改变一个字符。
4. 转换过程中的中间字符串必须是字典 strList 中的字符串,且strList里的每个字符串只用使用一次。
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例
6 abc def efc dbc ebc dec dfc yhn输出示例
4提示信息
从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4,如图:
数据范围:
2 <= N <= 500
原理
问题本质
这是一个单源最短路径问题,可以在无向图中建模:
- 节点:所有单词(包括beginStr、endStr和字典中的字符串)
- 边:两个单词之间恰好相差一个字符时存在边,边的权重为1
- 目标:求从beginStr到endStr的最短路径长度
BFS核心思想
广度优先搜索(BFS)天然适合求解无权图的最短路径:
- 分层遍历:从起始节点开始,按层逐层向外扩展
- 最短路径保证:第一层包含距离为1的所有节点,第二层包含距离为2的节点,以此类推
- 最早到达即最短:到达目标节点时,当前层数就是最短路径长度
代码
import java.util.*;public class Main {// 全局变量sum未使用,实际代码中未被调用static int sum = 0;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 读取字典中字符串的数量NString[] strings = new String[n];String start = scanner.next(); // 读取起始字符串beginStrString end = scanner.next(); // 读取结束字符串endStr// 创建包含所有单词的wordList(包括start和end)List<String> wordList = new ArrayList<>();wordList.add(start); // 添加起始字符串wordList.add(end); // 添加结束字符串// 读取N个字典字符串并加入wordListfor (int i = 0; i < n; i++) {strings[i] = scanner.next();wordList.add(strings[i]);}// 执行BFS计算最短路径长度int ans = bfs(start, end, wordList);System.out.print(ans); // 输出结果}/*** BFS广度优先搜索求最短转换序列长度* @param start 起始字符串* @param end 结束字符串* @param wordList 所有可用单词列表* @return 最短序列长度,如果无法到达返回0*/public static int bfs(String start, String end, List<String> wordList) {int len = 1; // 当前序列长度,初始为1(包含起始字符串)// set存储所有可用的单词Set<String> set = new HashSet<>(wordList);// visited记录已访问的单词,避免重复访问Set<String> visited = new HashSet<>();// 队列用于BFS,存储待处理的单词Queue<String> queue = new LinkedList<>();visited.add(start); // 标记起始字符串已访问queue.add(start); // 起始字符串入队queue.add(null); // 添加null标记,用于分层统计深度while (!queue.isEmpty()) {String str = queue.remove(); // 取出队列头部元素// 遇到null标记,表示当前层结束,需要进入下一层if (str == null) {if (!queue.isEmpty()) { // 队列非空,继续下一层len++; // 层数加1queue.add(null); // 添加新的null标记}continue;}// 对当前字符串的每个位置尝试替换char[] charArray = str.toCharArray();for (int i = 0; i < charArray.length; i++) {char old = charArray[i]; // 保存原始字符// 尝试将该位置替换为a-z的26个字母for (char j = 'a'; j <= 'z'; j++) {charArray[i] = j;String newWord = new String(charArray); // 生成新单词// 检查新单词是否在字典中且未访问过if (set.contains(newWord) && !visited.contains(newWord)) {queue.add(newWord); // 新单词入队visited.add(newWord); // 标记为已访问// 如果到达目标字符串,返回序列长度if (newWord.equals(end)) {return len + 1;}}}charArray[i] = old; // 恢复原始字符}}return 0; // 无法到达目标,返回0}
}105.有向图的完全联通
题目描述
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入描述
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
输出描述
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入示例
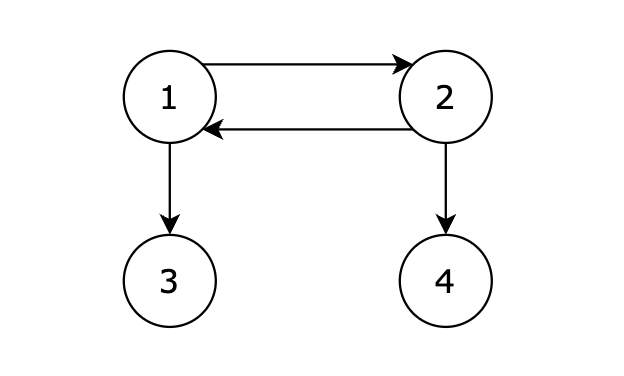
4 4 1 2 2 1 1 3 2 4输出示例
1提示信息
从 1 号节点可以到达任意节点,输出 1。
数据范围:
1 <= N <= 100;
1 <= K <= 2000。
原理
BFS+边访问数组
DFS+邻接表
BFS+邻接表
代码
import java.util.*;public class Main {static int sum = 0; // 未使用,冗余变量public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 节点数int k = scanner.nextInt(); // 边数// 使用二维数组存储边,空间浪费严重int[][] graph = new int[k][2];for (int i = 0; i < k; i++) {graph[i][0] = scanner.nextInt(); // 起点graph[i][1] = scanner.nextInt(); // 终点}scanner.close();boolean[] visited_node = new boolean[n + 1]; // 节点访问标记boolean[][] visited_bian = new boolean[n + 1][n + 1]; // 边访问标记(冗余!)// 执行BFSif (bfs(graph, visited_node, visited_bian)) {System.out.print(1);} else {System.out.print(-1);}}/*** BFS实现(版本1):遍历所有边寻找出边,复杂度O(K)*/public static boolean bfs(int[][] graph, boolean[] visited_node, boolean[][] visited_bian) {Queue<Integer> queue = new ArrayDeque<>(); // 队列存储待访问节点queue.add(1); // 从1号节点开始visited_node[1] = true; // 标记1已访问while (!queue.isEmpty()) {int node = queue.poll(); // 取出当前节点// 遍历所有K条边,寻找以node为起点的边(O(K)复杂度!)for (int i = 0; i < graph.length; i++) {if (graph[i][0] == node) { // 找到以node为起点的边int target = graph[i][1];// 同时检查边和节点是否访问过(逻辑冗余)if (!visited_bian[node][target] && !visited_node[target]) {visited_node[target] = true;visited_bian[node][target] = true;queue.add(target);}}}}// 检查是否所有节点都被访问for (int i = 1; i < visited_node.length; i++) {if (!visited_node[i]) return false;}return true;}
}import java.util.*;public class Main {static int sum = 0; // 未使用public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();// 构建邻接表:adjList[i]存储i的所有出边目标List<List<Integer>> adjList = new ArrayList<>();for (int i = 0; i <= n; i++) {adjList.add(new ArrayList<>()); // 为每个节点创建空列表}for (int i = 0; i < k; i++) {int s = scanner.nextInt();int t = scanner.nextInt();adjList.get(s).add(t); // s -> t}scanner.close();boolean[] visited_node = new boolean[n + 1];dfs(visited_node, adjList, 1); // 从1开始DFS// 检查连通性for (int i = 1; i < visited_node.length; i++) {if (!visited_node[i]) {System.out.print(-1);return;}}System.out.print(1);}/*** DFS递归实现:深度优先遍历*/public static void dfs(boolean[] visited_node, List<List<Integer>> adjList, int cur) {visited_node[cur] = true; // 标记当前节点List<Integer> neighbors = adjList.get(cur); // 获取所有邻接节点if (!neighbors.isEmpty()) {for (int next : neighbors) {if (!visited_node[next]) { // 未访问才递归dfs(visited_node, adjList, next);}}}}
}import java.util.*;public class Main {static int sum = 0; // 未使用public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();// 构建邻接表List<List<Integer>> adjList = new ArrayList<>();for (int i = 0; i <= n; i++) {adjList.add(new ArrayList<>());}for (int i = 0; i < k; i++) {int s = scanner.nextInt();int t = scanner.nextInt();adjList.get(s).add(t); // s -> t}scanner.close();boolean[] visited_node = new boolean[n + 1];if (bfs(visited_node, adjList)) {System.out.print(1);} else {System.out.print(-1);}}/*** BFS实现(推荐):广度优先遍历*/public static boolean bfs(boolean[] visited_node, List<List<Integer>> adjList) {Queue<Integer> queue = new ArrayDeque<>();queue.add(1); // 从1开始visited_node[1] = true; // 标记起点while (!queue.isEmpty()) {int node = queue.poll(); // 取出当前节点// 只遍历当前节点的邻接表(O(deg(node)))List<Integer> neighbors = adjList.get(node);for (int next : neighbors) {if (!visited_node[next]) { // 未访问visited_node[next] = true;queue.add(next);}}}// 检查所有节点是否可达for (int i = 1; i < visited_node.length; i++) {if (!visited_node[i]) return false;}return true;}
}