【论文阅读】Pore-scale modeling of complex transport phenomena in porous media

Title：Pore-scale modeling of complex transport phenomena in porous media
Journal：Progress in Energy and Combustion Science
Author：陈黎等，西安交通大学

本文仅为阅读记录，并非全文，获取全文可访问https://doi.org/10.1016/j.pecs.2021.100968

摘要：

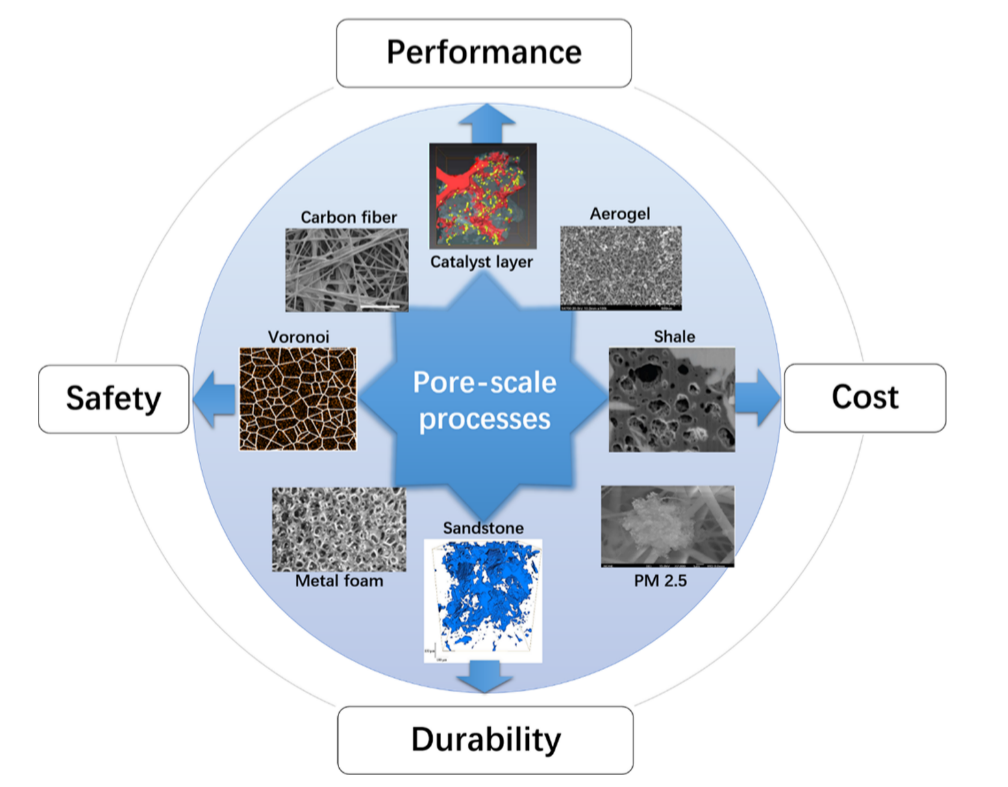
多孔介质在广泛的科学和工程问题中起着重要作用。近年来，随着它们在能量转换和存储设备(如燃料电池、电池和超级电容器)中的应用越来越多，人们已经认识到，发生在孔隙和不同组分界面上的输运过程和反应会显著影响多孔介质的性能。传统的基于代表性单元体积(REV)的数值模型没有很好地描述这些孔隙尺度的输运现象，甚至忽略了这些现象。孔隙尺度建模是模拟多孔介质中孔隙尺度传输和反应的有效工具，因为它能够准确地表征这些过程，并提供重要变量的分布细节，这对于目前的实验技术来说是具有挑战性的，因为缺乏原位测量能力或由于有限的空间和时间分辨率。本文综述了孔隙尺度模拟技术的研究进展和面临的挑战。讨论了孔隙尺度建模在地球科学、聚合物交换膜燃料电池(PEMFC)和固体氧化物燃料电池(SOFC)等领域的实际应用。给出了孔隙尺度建模的显著结果，并讨论了孔隙尺度模型发展面临的挑战。这篇深入的综述旨在全面介绍孔隙尺度建模可以在相关科学和工程系统的发展中发挥作用的关键方面。

1 引言

多孔介质的参数包括孔隙度、孔径、比表面积、弯曲度、渗透率和相对渗透率、有效扩散系数/导热系数、有效反应速率等。

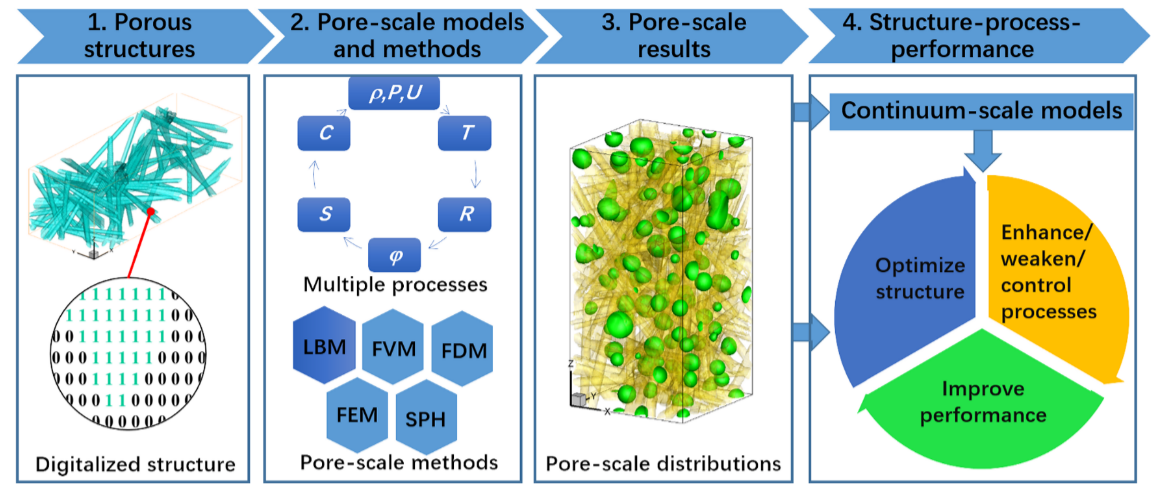
孔隙尺度建模的能力和效率取决于图所示的四个主要组成部分:(1)准确描述不同组成部分的孔隙结构和分布细节[32,43-46];(2)建立多孔介质侧输运现象的物理化学模型[29,31,47]，开发高效鲁棒的数值方法求解控制方程并进行孔隙尺度建模[35,36,42];(3)分析相关变量的孔隙尺度时空演化，深入了解其机制，研究孔隙结构和界面特征对输运过程的影响;最后(4)基于孔隙尺度结果，或基于放大孔隙尺度结果的连续尺度建模结果，通过改变孔隙结构、物理化学性质或操作条件来增强、减弱或控制多孔介质中的输运过程，以获得更好的体系性能。

Tartakovsky等人综述了多相流孔隙尺度模拟的数值方法，包括晶格玻尔兹曼方法(LBM)、蒙特卡罗方法、粒子方法、孔隙网络方法和传统的计算流体力学(CFD)方法。

电化学装置中传输过程的孔隙尺度建模，读者可以参考以下参考文献

1. Lattice Boltzmann simulation of proton exchange membrane fuel cells
   – A review on opportunities and challenges. Int J Hydrogen Energy
   2016;41(47):22221–45.
2. Lattice Boltzmann modeling of transport phenomena in fuel cells and
   flow batteries. Acta Mechanica Sinica 2017;33(3):555–74.
3. Mesoscale modeling in electrochemical devices—a critical
   perspective. Prog Energy Combust Sci 2019;71:118–42.
4. Progress in 3D electrode microstructure modelling for fuel cells and
   batteries: transport and electrochemical performance. Prog Energy
   2019;1

2 多孔结构成像与计算重建

获得高保真多孔介质几何细节的方法可分为两类：直接实验成像法和计算重建法。

2.1 实验成像

在直接成像中，采用XCT[48]、FIB-SEM[49]和电子断层扫描[50]等实验成像技术获得多孔介质的三维微观结构。

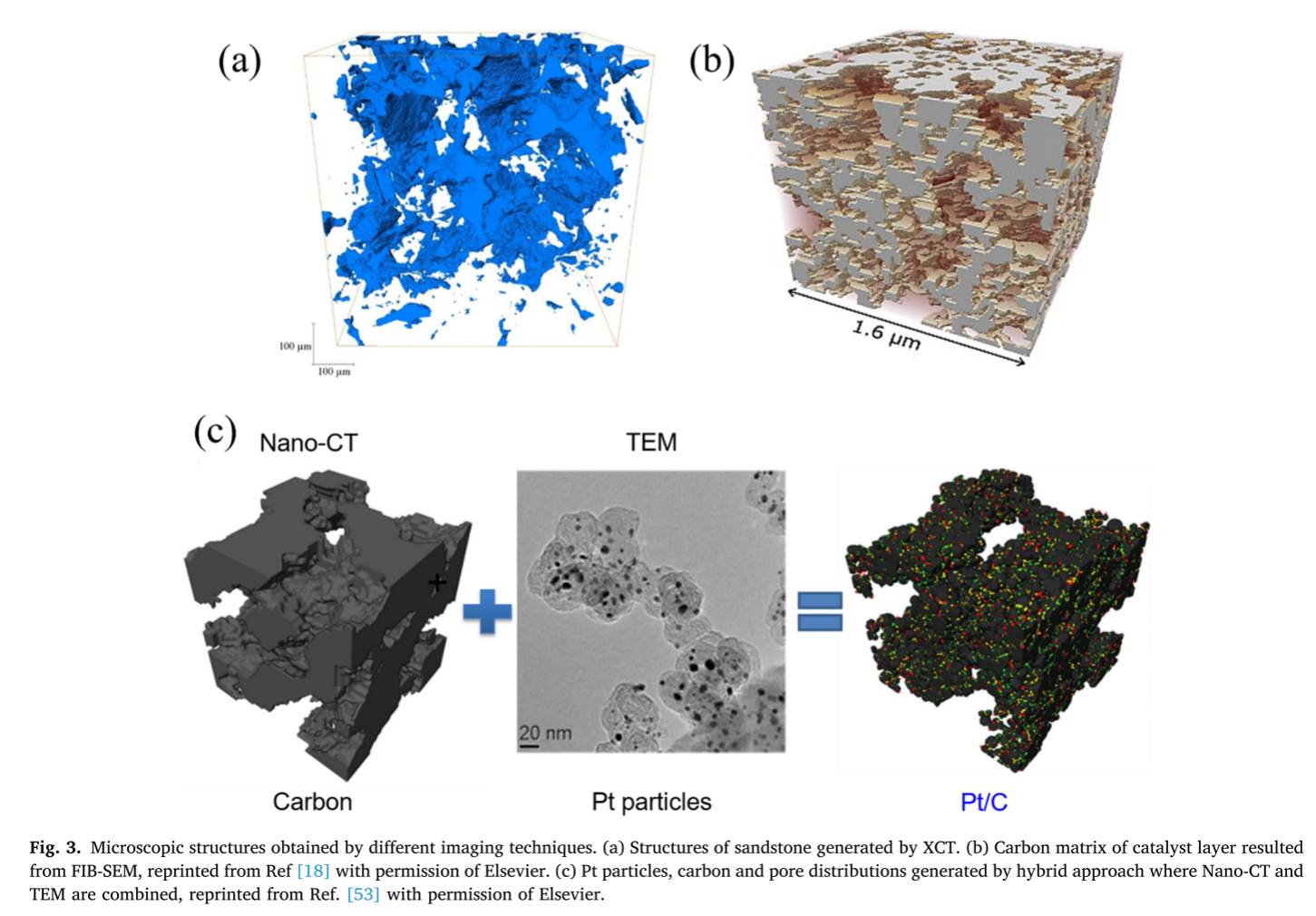
图3(a)为分辨率为1 μm的XCT获得的砂岩孔隙结构。
图3(b)显示了在x, y和z方向上分辨率为3.4 nm × 3.4 nm × 13.6 nm的FIB-SEM所获得的PEMFC中催化剂层(CL)的结构[18]。
图3©为混合方法提供的CL的孔隙结构，其中采用纳米ct提取次生孔隙和碳矩阵，采用TEM获得Pt分布[53]。

对于特征长度为几纳米的多孔介质，通常采用FIB-SEM。采用FIB对多孔介质进行研磨，形成新的暴露表面，然后利用扫描电子显微镜对表面进行成像。然后将连续的2D图像组合在一起生成3D结构。

2.2 计算重建

现有的方法可以分为两种:统计重建方法和基于过程的重建方法[44]。统计重建方法利用静态约束生成多孔结构，而静态约束通常来自二维图像。另一方面，基于过程的重建方法试图模拟产生当前多孔结构的过程。

统计重建方法：第一步是获得多孔介质的二维图像。有几种成熟的高分辨率二维成像方法，如扫描电子显微镜和透射电镜，与三维成像技术相比，这些二维成像技术更容易获得。基于多孔介质的高分辨率二维图像，可以识别拓扑特征并评估统计参数(孔隙度、孔径、粒径、两点统计函数等)。在遵循这些结构参数的前提下，实施了一些精心设计的程序来构建复杂的微观结构。

• 模拟退火程序
• 马尔可夫链蒙特卡罗(MCMC)方法
• 离散元法(DEM)
• 四重奏结构生成集(QSGS)
• 。。。
  
  图 4(a)的扫描电子显微镜图像中可以观察到，纤维电极由形状近似为长圆柱体的随机分布的纤维组成。图4(b)显示了不同孔隙率和纤维直径重构的电极结构[67]。

3 孔隙尺度数值方法、边界条件和界面格式

3.1 控制方程

孔隙尺度数值模型基于质量守恒、动量守恒、热能守恒等守恒原理。
质量和动量的守恒方程也被称为纳维-斯托克斯方程。（Navier-Stokes）

孔隙尺度模拟采用了不同的数值方法。

• 传统的CFD方法，如有限型方法(有限体积法(FVM)、有限元法(FEM)和有限差分法(FDM))在给定一组合适的边界条件下，通过方程离散直接求解NS方程[36,79]。
• 孔隙网络模型（PNM）也被广泛用于研究多孔介质中的输运过程，该模型将实际孔隙结构抽象为人工孔隙网络，孔隙表示由喉道连接的大空隙空间的位置。
• 介观数值方法，如晶格玻尔兹曼方法(LBM)，由于其动力学性质，具有在多孔介质复杂边界上灵活指定变量的优点，因此在模拟多孔介质中的流体流动和多相流问题中得到了广泛的应用[37,82]。

3.2 晶格玻尔兹曼方法的一般描述

与基于Navier-Stokes方程直接离散化的传统CFD方法相比，LBM是一种直接从Boltzmann方程导出的基于动力学理论的数值方法[89]，包括编程的简单性、内在的并行性，以及对复杂固体边界、多相流和多物种输运的直接处理[83-88]。

3.3 边界条件和界面格式

LBM中的边界条件也用分布函数表示。在LBM仿真中，碰撞完全是局部的，而流步骤需要来自相邻节点的信息。然而，对于边界或接口节点，相邻节点要么不存在，要么属于其他组件，这使得信息难以直接传播。

3.3.1 无滑移流动边界条件

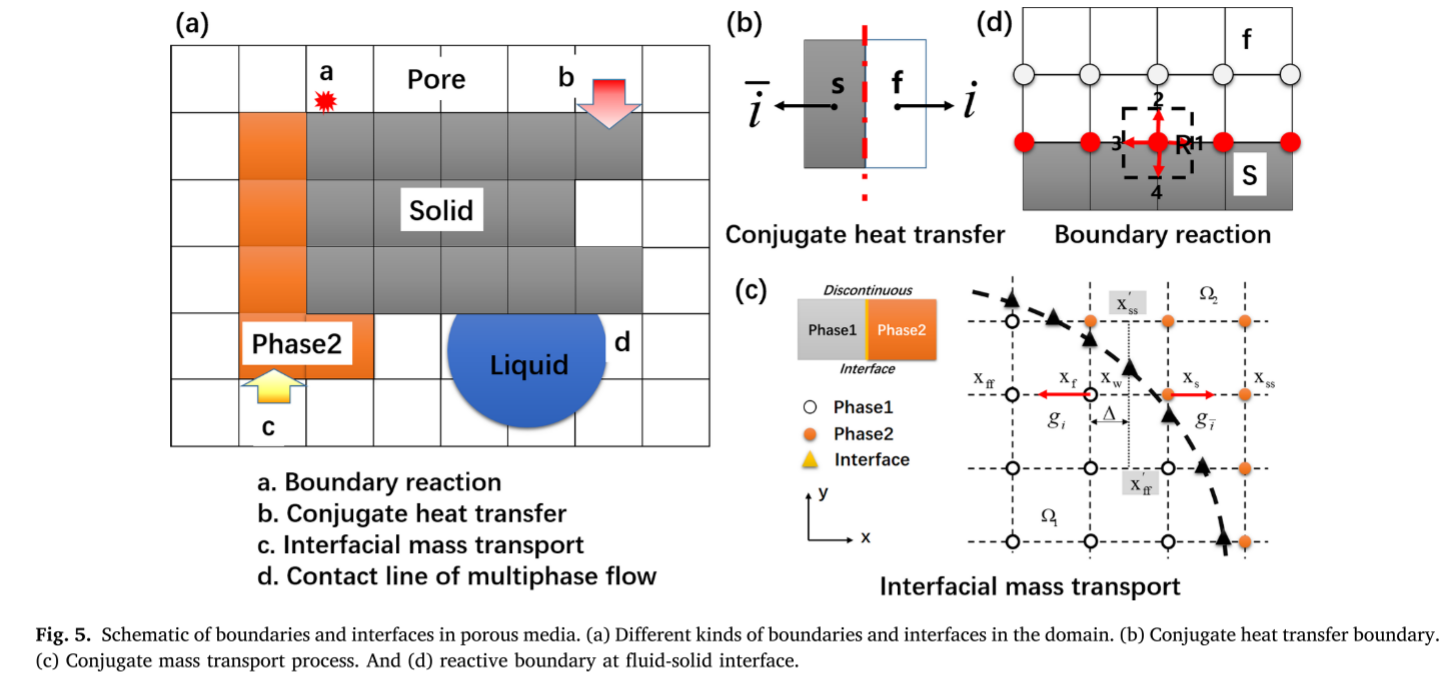
对于多孔介质中的流体流动，在流体–固体界面处施加无滑移边界条件（no-slip boundary condition），这意味着：紧邻固体节点的流体节点的速度等于该固体节点的速度（即流体在界面上“粘附”在固体上，不会滑动）。在格子Boltzmann（LB）方法框架下，最常用的实现方式是简单反弹（bounce-back）边界条件，如图5(b)所示，它通过让粒子分布函数在遇到固体壁面时反向反弹，从而满足无滑移条件。

3.3.2 界面传热

具有不同热性能的不同组分之间的传热称为共轭传热，它满足温度和热流密度的连续性条件(参见图 (b))。
式中f和s分别表示流体相和固相。共轭问题的主要挑战是方程(6a-6b)描述的界面条件是狄利克雷边界和诺伊曼边界的组合。

3.3.2.1 稳态热LB模型

略

3.3.2.1 非稳态热LB模型

略

3.3.3 界面质量输运

与传热不同的是，温度在界面上是连续的，对于质量传递，根据亨利定律，在不同组分的界面上浓度不是连续的，这种不连续性被称为浓度跳变。

3.3.4. 化学反应

略

3.3.5 流体-流体和流体-固体界面

对于多相流体系统，需要附加方程来描述两相界面运动和界面处的界面张力。流体体积法、水平集法和相场法是常用的三种界面捕获方法。在这三种方法中，都引入了一个指示函数来表征不同的相，轨迹流体-流体界面的运动并计算界面张力。然后，通过局部流体性质和界面张力，将界面捕获方法与NS方程耦合，建立两相流动力学模型[36,136]。

4 输运过程和宏观输运性质

孔隙尺度建模可以提供相关变量(速度、压力、温度、浓度等)在孔隙尺度上的分布，这些变量难以用实验方法测量[156]。这样的孔隙尺度知识有助于更好地设计和控制多孔介质中的输运过程[157]。基于这些孔隙尺度分布，可以计算多孔介质的宏观输运性质(渗透率、有效扩散系数、有效导热系数等)，这些对多孔介质的设计具有重要意义。这些输运特性也可以被放大到连续尺度模型中，以提高连续尺度模型的精度。当应用孔隙尺度模型预测宏观输运性质时，模型的样本量必须足够大，以达到REV[28,158,159]。

博主按：
Representative Elementary Volume
—— 代表性体积单元 或 代表性基本体积
是指：
在多孔介质中，足够大到能够代表整体统计特性、又足够小到可认为局部均匀的最小体积单元。
换句话说：
如果你在岩石、GDL、催化层中取一个很小的区域，测得的孔隙率、渗透率等值会随位置变化很大；但如果取的区域逐渐变大，到一定体积之后，这些参数趋于稳定不变；这时对应的最小体积，就是 REV。

4.1 单相流体的流动和渗透率

只有在相对简单的多孔结构中，渗透率与多孔介质几何形状之间才存在解析表达式。例如，在由均匀球体填充形成的多孔介质中，对于低雷诺数下的黏性蠕动流动，Kozeny–Carman 方程是广泛采用的经验模型 [162,163]。需要注意的是，渗透率仅取决于多孔介质自身的结构，而与流体性质无关，因此又被称为本征渗透率（intrinsic permeability）。然而，当孔径较小，或者 Knudsen 数（Kn，气体分子平均自由程与多孔介质特征孔径的比值）较大时，会出现滑移现象（slippage phenomenon）。这种滑移使得流体在孔壁处不再严格满足“无滑移边界条件”，从而导致实测渗透率高于本征渗透率，这种情况被称为视渗透率（apparent permeability）[165,166]。因此，表观（视）渗透率不仅受多孔结构的影响，还受到操作条件和流体性质的共同影响 [87]。

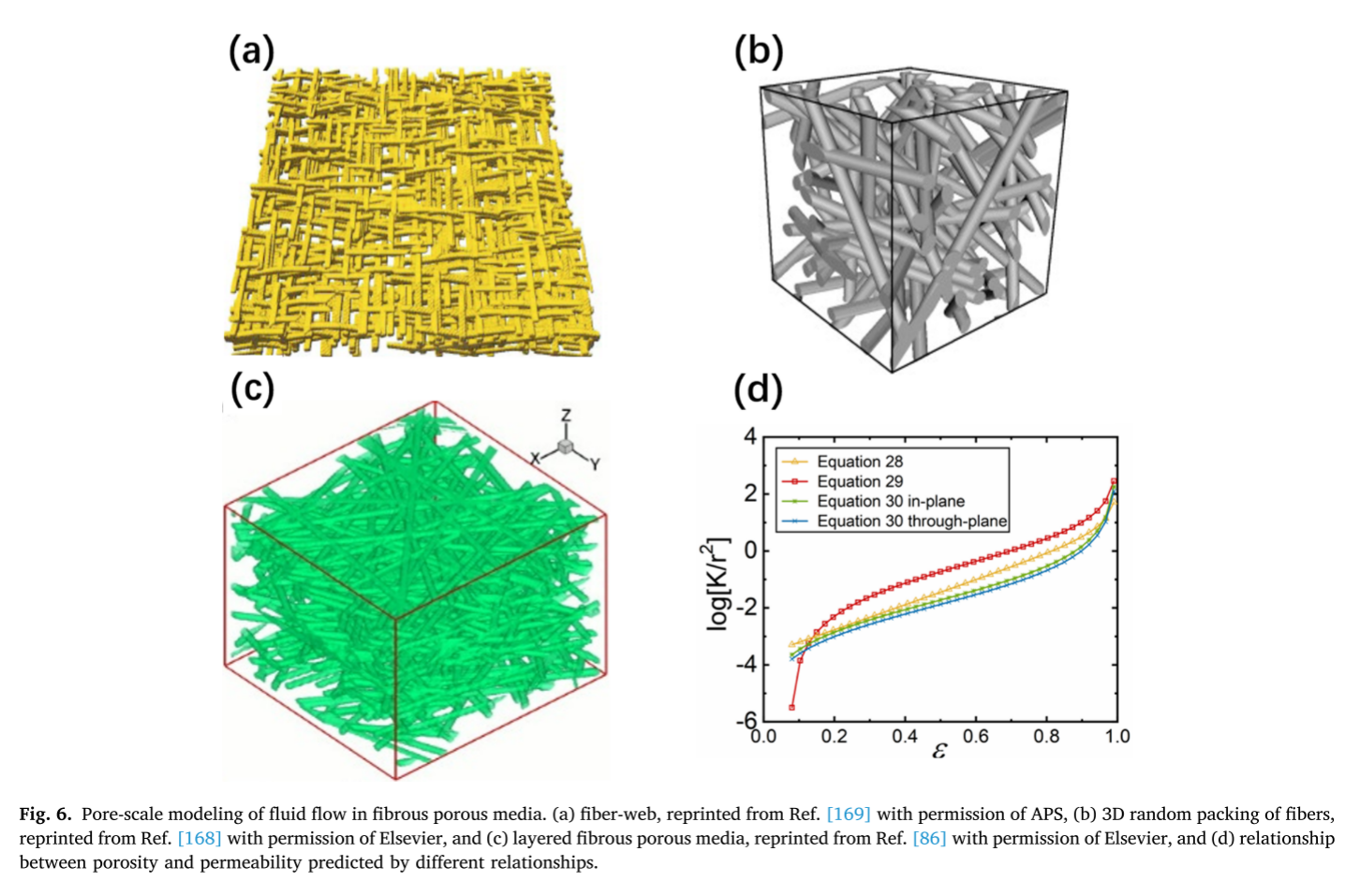
4.2 传热

有效热导率(λeff)是多孔介质的基本热性质之一[191,192]。有效导热系数的准确计算对于控制热流密度和设计多孔介质具有重要意义。理论上，λeff是各组分体积分数εi和导热系数λi的函数，可由λeff = f(λi，εi)确定。f的表达式取决于不同成分的分布细节。

4.3 扩散

对于二元扩散，Fick定律已成功用于描述整体扩散；而对于包含三种或更多组分的扩散过程，则可采用Stefan-Maxwell定律。当孔隙特征长度d与平均自由程相当甚至更小时，Knudsen扩散便成为主导因素。

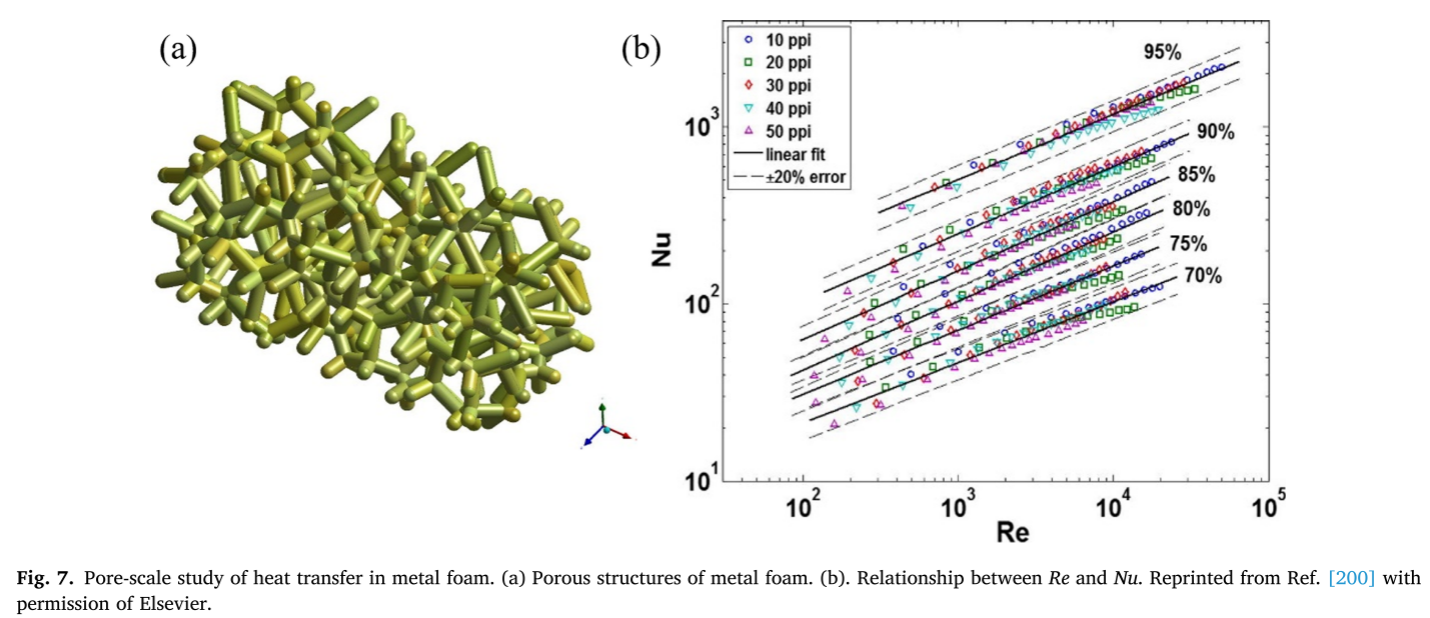
目前，确定局部孔隙尺寸主要采用两种方法：最大球体法[68]，以及13方向平均法[206]。

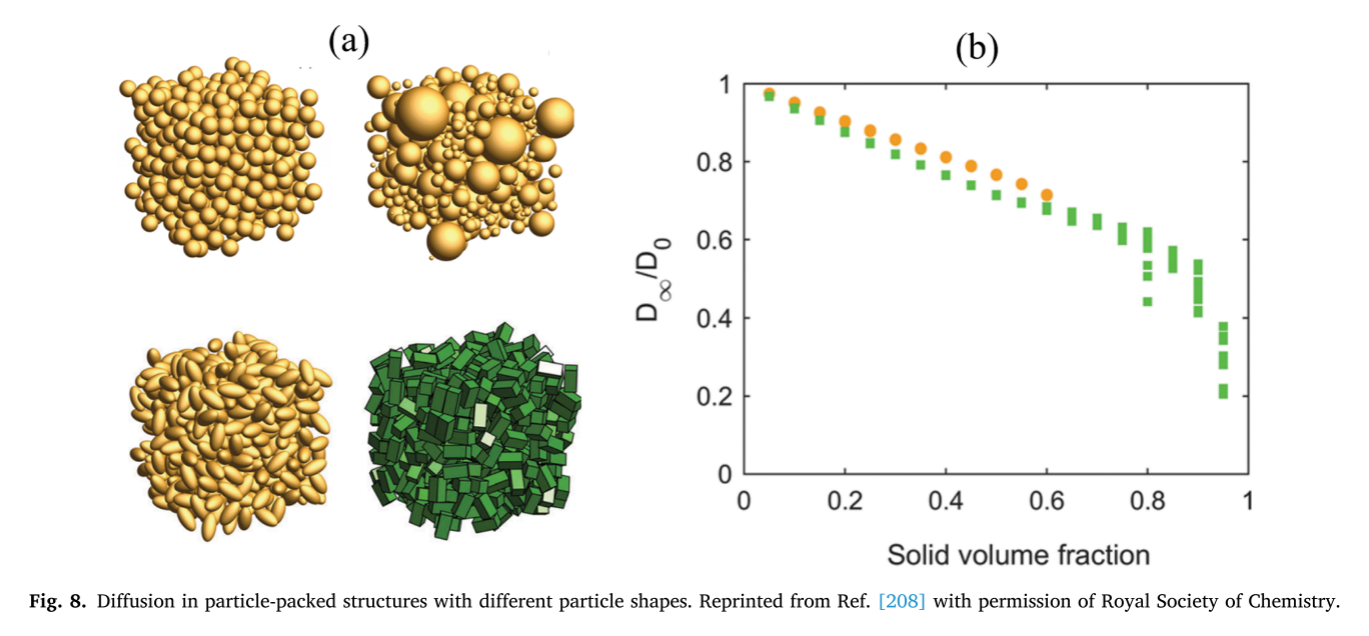
4.4 迂曲度

弯曲度的定义是多孔介质在宏观输运方向上真实输运长度Le的平均长度与多孔介质L的直接长度之比。
曲度不仅取决于多孔介质的结构和形态，还取决于所研究的具体传输过程。在文献中，已经计算了不同类型的曲折，如几何曲折、液压曲折、扩散曲折和电气曲折，但对于它们之间的关系没有明确的共识[210,211]。

对于液压弯曲性，Duta等人[210]直接根据流体速度场推导出以下表达式

其中u是速度，x是考虑的方向。由于方程(36)的简单性，越来越多地用于计算扭曲度。

4.5 挑战

从上面的回顾可以清楚地看出，分析结构参数对输运过程的影响，从而对宏观输运性质的影响是一项繁琐的任务。如果可能的话，提出不同类型多孔介质的宏观输运性质与结构参数之间的通用公式是非常具有挑战性的。然而，了解多孔结构与相关物理变量的孔隙尺度分布之间的潜在关系对于控制多孔介质的输运过程和改善多孔介质的性能非常重要[215,216]。Jin等[71]对多孔泡沫、填充球和Bentheimer砂岩三种不同多孔介质中的流体流动进行了孔隙尺度研究。计算了随机多孔热均质材料的两点相关函数和间隙流向速度场的欧拉相关函数。结果表明，这两个函数都是近程的，呈指数衰减，且具有相似的模式。在第5节中，我们会发现，与单相流体流动相比，多孔结构和润湿性对多相流动的影响更为复杂，了解多孔结构、表面特征和孔隙尺度多相分布及动力学行为之间的相互作用非常重要。

5 在地球科学中的应用

5.1 地下多孔介质中的多相流动

多孔介质中的多相流在许多地球物理过程中都很常见，如多孔岩石中的油气开采、盐水层或碳氢储层中二氧化碳的注入和储存、非水相液体(NAPL)污染地下水的修复等[34,217]。对于多孔介质中的多相流动，不同的流体相共享相同的复杂孔隙空间。不同相的动态流动行为和分布受多种因素的影响，包括润湿性、毛细数、粘度比以及流动过程(吸胀和排水)[34]，因此描述这一现象是一项具有挑战性的任务。

值得一提的是，darcy尺度两相流模型与孔隙尺度数值模拟在不同尺度上是互补的方法。达西尺度的两相流模型应用于工程规模来解决实际问题。但它在理论上有一定的局限性，这可以用孔隙尺度模型来解释。另一方面，虽然孔隙尺度建模可以揭示多孔介质内部发生的基本物理现象，但如果不将模拟结果升级为达西尺度模型，通常无法直接用于实际应用。

博主按：
孔隙尺度看“细节” —— 研究流体在每一个孔道、固体表面的真实运动。
达西尺度看“整体” —— 把多孔材料当作“连续介质”，研究宏观的平均流动规律。

项目	孔隙尺度（Pore scale）	达西尺度（Darcy scale）
研究对象	真实的孔隙结构：单个孔、孔喉、纤维间隙	把整个多孔介质当成均质的“块体”
描述方法	微观流体力学（Navier–Stokes方程、LBM、相场法等）	宏观经验定律（Darcy定律、多相Darcy方程等）
典型尺寸	微米 ~ 纳米级	毫米 ~ 厘米 ~ 工程尺度
变量分布	在每个孔内有局部速度、压力、浓度场	变量是空间平均的（例如平均压力梯度）
输入数据	孔隙几何（μCT扫描、随机重建）	宏观参数（渗透率、相对渗透率、有效扩散系数）
输出结果	微观流动场、界面运动、相分布	工程尺度流量、压降、含水率、性能预测
适用目标	解释机理、发现规律	工程设计、系统模拟

5.1.1 相对渗透率

相对渗透率和毛管压力曲线是连续尺度下表征多孔介质中两相流动的最重要特征。毛细管数(Ca)[27,225-227]、粘度比[27,226-228]、润湿性[27,226-229]和润湿性非均质性[229-232]等不同参数对相对渗透率的影响已经通过孔隙尺度建模进行了广泛的研究，但结论相当复杂。

5.1.2 毛细管压力-饱和度关系

5.1.3 非混相两相驱替

非混相两相驱替包括用非润湿流体置换湿性流体时的排水，以及用润湿流体置换非润湿流体时的吸胀。在不同的流量、粘度比、润湿性条件和孔隙几何形状下，两相驱替过程中可以观察到不同的流动模式。

除了黏性力和毛细力之外，惯性力对两相流驱替过程的重要性也已被认识到。Zacharoudiou 等人 [272] 分析了 Haines 跳跃（Haines jump）发生区域附近的局部两相流动力学，结果发现，当惯性力变得显著时，Haines 跳跃事件会非常迅速地发生，这通常会引起局部压力和相分布的重新调整，例如局部的自吸（imbibition）或断裂（snap-off）现象 [272,273]。Ferrari 等人 [274] 和 Zacharoudiou 等人 [275] 发现，在低速自吸过程中，孔隙充填事件也可能非常快速，这是由于表面能的突然释放所致。孔隙充填过程不仅由毛细数和黏度比决定，还受到 Ohnesorge 数的影响，后者表征了黏性力相对于惯性力和毛细力的重要性。最近，Chen 等人 [154] 在不同流动条件下研究了惯性力对真实三维数字岩石中排驱模式的影响。结果表明，在相同毛细数条件下，惯性效应越强，形成的流动通道（指状渗流）越多。

5.1.4 其他实际应用

在二氧化碳地质封存过程中，CO₂ 团簇和气团的毛细滞留效应可以通过排驱与随后的自吸过程模拟来定量分析。Jiang 等人 [276] 研究了界面张力（interfacial tension, IFT）对 CO₂ 滞留的影响，结果发现：较高的界面张力会导致更多的 CO₂ 被滞留，并形成更大的滞留团簇（如图 13 所示）。此外，由于毛细力更强，高界面张力条件下的毛细滞留也更加稳定。研究者还分析了自吸过程开始前 CO₂ 初始分布的影响 [277]。结果表明，初始 CO₂ 团簇的连通性越高、球形度（表示与球体形状的相似程度）越大，其残余毛细滞留的 CO₂ 就越少。
Bakhshian 等人 [231] 研究了润湿性非均匀性对 CO₂ 滞留的影响。他们在模型中随机生成了具有 CO₂ 亲润特性的固体表面区域，结果发现：CO₂ 亲润区域越多，被滞留的 CO₂ 相越容易分散成多个团簇，连通性也随之降低。这些孔隙尺度的研究对于优化二氧化碳地质封存的运行策略具有重要意义。

在石油工程中，孔隙尺度模拟同样有助于深入理解提高采收率（EOR）的机理。
Akai 等人 [278] 利用格子 Boltzmann 方法（LBM）耦合离子传输方程，研究了多孔介质中低盐度水驱油过程，并考虑了由于离子在固体表面吸附/解吸导致的润湿性改变。结果表明，注入低盐度水的时机对最终流体分布具有显著影响。Xie 等人 [279] 建立了一个用于多相粘塑性流体流动的 LBM 模型，以描述聚合物溶液的非牛顿流动行为，并用该模型模拟了不同二维多孔介质中的非牛顿流体驱替过程。结果显示，相比剪切变稀流体（shear-thinning fluid），剪切变稠流体（shear-thickening fluid）在提高采收率方面表现更好，因为它具有更强的能力将驱替液从高渗透层引导至低渗透层。他们随后将该模型扩展到三相流，用于研究分散聚合物驱（dispersed polymer flooding）提高采收率的机理 [280]。Wei 等人 [281] 则采用 Shan–Chen 型 LBM 模型模拟多相流动，并利用带偶极子的结构来表征表面活性剂的两亲特性，从而研究表面活性剂驱油的机理。基于该模型，他们分析了表面活性剂对液滴变形、液滴从固体表面脱离及通过狭窄孔喉的影响，以及在多孔介质中两相驱替行为的变化。

5.2 多孔介质中固体结构演化的反应输运

在地球科学中，伴随多孔介质固体结构演化的反应–传输过程非常常见，例如二氧化碳的地质封存 [282]、提高采收率的酸注入 [283]、水环境中的生物膜生长 [284]、核燃料处置 [33] 等。固体结构演化的起源可能不同，例如由化学反应引起的溶解/沉淀、由热传递引起的熔化/凝固，或颗粒的迁移与团聚等。这种固体结构的演化会受到孔隙尺度传输过程的显著影响，反过来也会控制传输过程所发生的空间域 [285]。除了需要准确地模拟多孔介质中的多种传输过程和反应之外，孔隙尺度建模还应精确描述流体–固体界面的动态变化。为了捕捉或追踪流体–固体界面的变化，研究者已经采用了多种数值方法，例如元胞自动机（CA）方法、体积分数法（VOF）、水平集法（LS）、相场法（phase field method）等 [286]。

5.3 挑战

在研究多孔介质中的多相流和反应输运现象时，仍有一些挑战需要解决。首先，不同的研究表明，表征多孔介质中多相流动的重要宏观尺度性质是由详细的孔隙尺度相分布决定的。然而，目前的连续介质尺度模型都不能考虑所有的孔隙尺度信息。探索宏观输运性质与微观相分布之间的确切关系仍然是一个具有挑战性的任务。其次，多孔介质中两相驱替的孔隙尺度数值研究大多集中在排水过程上。渗吸作用，特别是具有角膜层的角状多孔介质中的强烈渗吸作用仍然不太清楚[265]。角膜流和主弯月面流之间的竞争使得强渗吸过程更加复杂。

6 质子交换膜燃料电池的应用

在质子交换膜燃料电池、固体氧化物燃料电池和直接甲醇燃料电池等燃料电池中，多孔电极被广泛用于强化传输过程和促进电化学反应。例如，PEMFC内部的气体扩散层(GDL)、微观多孔层(MPL)和CL都是具有复杂孔结构的多孔介质[299]。复杂的物理-电-化学过程同时发生在这些多孔组分中。

6.1 气体扩散层

目前广泛使用的气凝胶为碳纤维基多孔介质，其典型直径为6-10μm，厚度为100-300μm，孔隙率为0.6-0.9，孔径为10-100μm[]。随着碳纤维的层层放置，最广泛使用的碳纸GDL在平面内(IP)和穿透平面(TP)方向之间显示出高度的各向异性。总体上，GDL具有薄、非均质、各向异性的多孔介质特征。在气液两相流中，气液两相流动同时发生相变、传质、传热和电子传导过程。

6.1.1 气体扩散层中的多相流

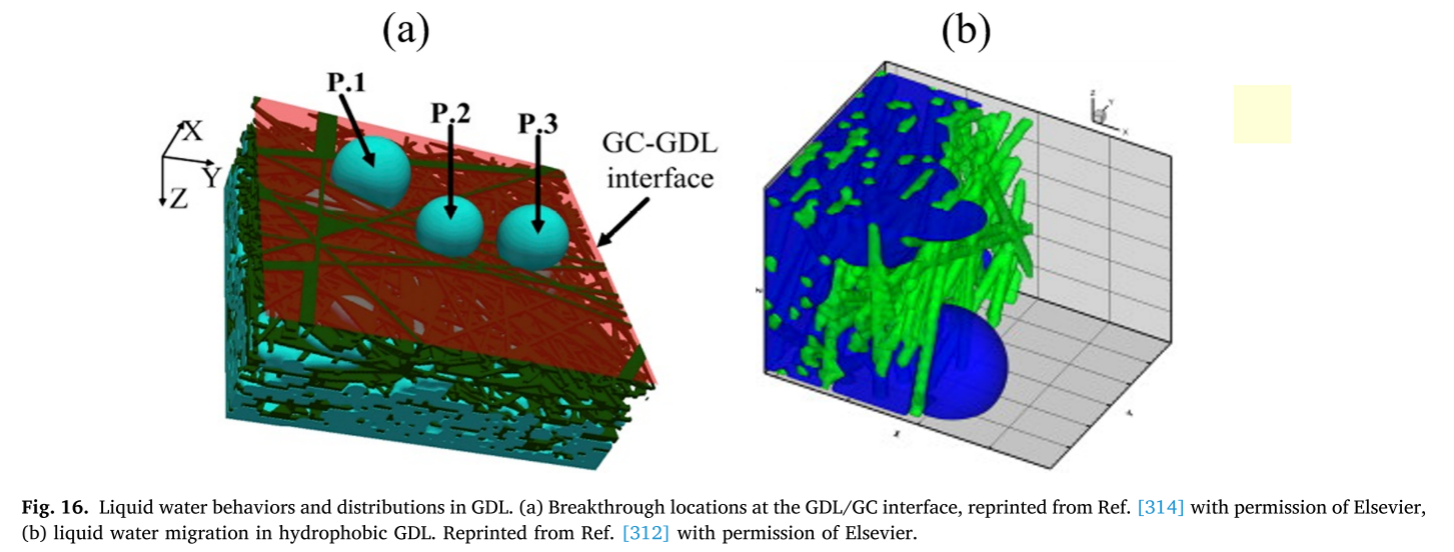
在疏水性的气体扩散层（GDL）中，根据毛细指进机制，液态水在渗透时总是优先进入孔径最大的孔隙，因为那里局部阻力最小 [309–314]。在这种毛细指进机制下，GDL 贯穿方向上的水饱和度曲线呈现凹形特征[312]。当液态水突破 GDL 后，会在 GDL/集流板（GC）界面的随机或优先位置形成液滴。文献 [314] 中在孔隙尺度上研究了 22 个随机重构的 GDL 的液态水突破行为（如图 16(a) 所示），并对不同突破位置之间的距离进行了详细分析。结果表明，这些距离可以用正态分布函数来描述。需要注意的是，对于毛细指进过程，主导作用的力是毛细力，而黏性力、惯性力和重力的影响可以忽略。因此，在许多文献中，当进行 GDL 中两相流的孔隙尺度数值模拟时，通常将流体密度比和黏度比设为 1，因为这些比值只会影响黏性力、惯性力和重力 [309–312,315]。

6.1.2 宏观输运性质的预测

6.2 催化层

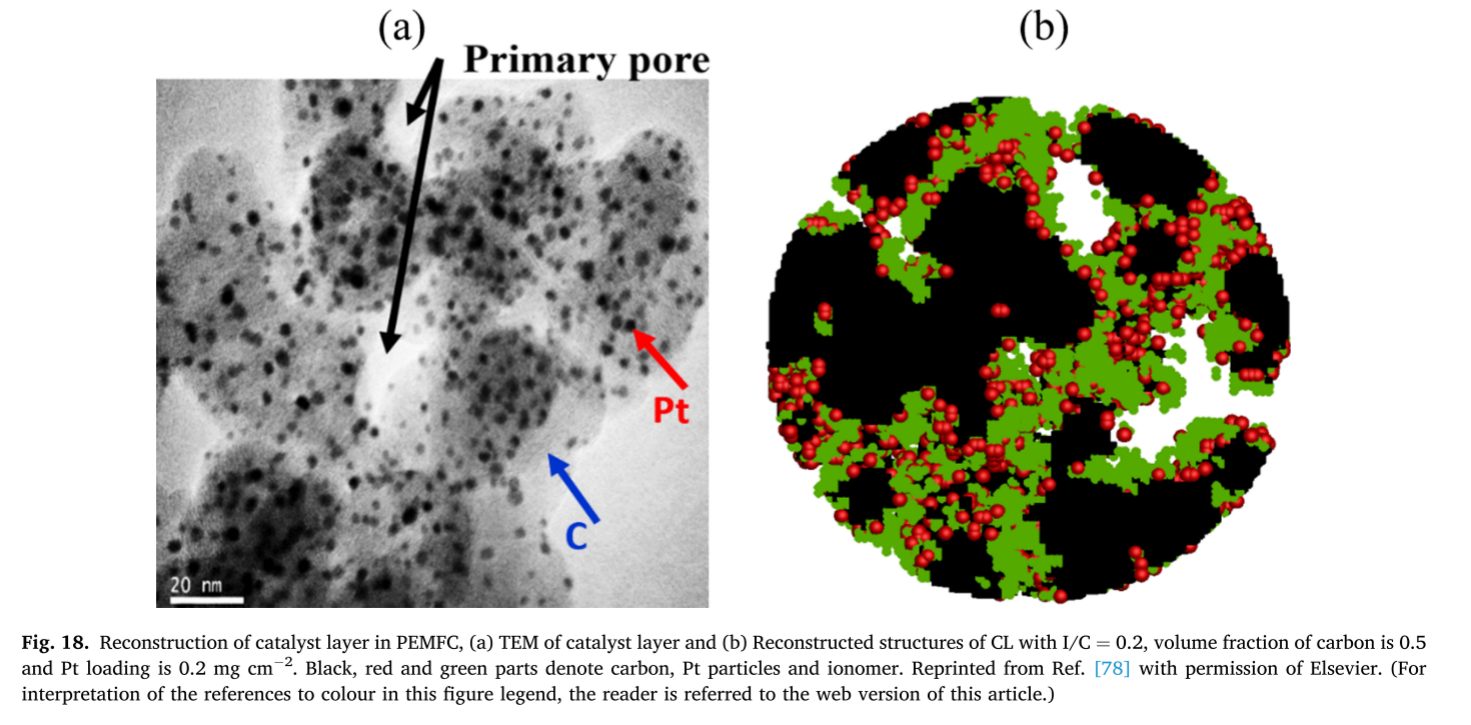
在质子交换膜燃料电池（PEMFC）中，催化层（CL）是发生电化学反应的区域，化学能在此转化为电能。为了形成用于电化学反应的三相界面（TPB），催化层内部需要多种组分共存。目前常用的催化层通常由碳（用于电子传导）、Nafion 离聚物（用于质子迁移）、铂颗粒（作为催化剂）以及用于反应气体与生成水传输的孔隙空间组成，如图 18 所示 [78]。

6.2.1 有效输运性质的预测

6.2.2 液态水的动力学和分布

6.2.3 Low Pt loading transport resistance

从以上讨论可以看出，在质子交换膜燃料电池（PEMFC）的多孔电极内部，多相流动、相变、传热、传质以及电化学反应是同时发生的。目前，还没有能够全面考虑所有这些过程的孔隙尺度模型。首先，尽管已有大量孔隙尺度模拟用于研究不同条件下的气-液两相流动，但仍然缺乏能够耦合多相流与传热过程的孔隙尺度研究。相应的孔隙尺度模型仍需要进一步发展。此类模型的建立将对于深入理解复杂的相变多相流动过程（例如蒸汽扩散、相变多相流、毛细冷凝、毛细指进等）具有重要意义。

其次，开发能够充分考虑催化层（CL）内部多相反应传输过程的孔隙尺度模型是一项极具挑战性的任务。迫切需要开展孔隙尺度研究，以揭示局部传输阻力的形成机理，探索纳米尺度结构与反应传输过程之间的相互作用，研究水的动态行为，并理解由材料劣化引起的结构演化与反应传输过程之间的耦合机制 [338,351]。值得注意的是，在催化层内部，孔径仅为数纳米的孔隙非常普遍。孔隙尺度模型应能够考虑反应传输过程中纳米尺度效应的影响，例如滑移流动、表面扩散、表面吸附与解吸等 [43,364]。

最后，质子交换膜燃料电池（PEMFC）的多孔电极本质上具有多尺度特征。孔径从催化层（CL）中的几纳米，变化到微孔层（MPL）中的数百纳米，再到气体扩散层（GDL）中的数十微米。跨越 CL、MPL 和 GDL 界面的反应传输过程目前仍远未被充分理解 [365]。Zhang 等人 [366] 开发了一种孔隙尺度模型，用于模拟在同时解析 GDL 和 MPL 微观结构的条件下的多相流与反应传输的耦合过程。实际上，在多尺度电极中开展能够同时考虑跨层传输过程的孔隙尺度建模，需要极高甚至难以承受的计算资源。因此，能够降低计算量并加速模拟过程的孔隙尺度建模方法极为迫切且具有重要意义。

7 固体氧化物燃料电池的应用

固体氧化物燃料电池（SOFC）因其优异的能量转换效率 [367]、燃料选择的灵活性 [368] 以及低污染特性而受到广泛关注。SOFC 的结构由一层固体陶瓷电解质夹在阳极和阴极之间组成 [368]。在阳极处，氢气与氧化物离子发生反应，生成水蒸气并释放电子；在阴极处，氧气被还原生成氧化物离子 [368]。

7.1 电极的电化学模型

7.1.1 运输模式

7.1.2 电化学反应

7.2 电极微结构模拟

7.2.1 电化学特性的预测

连续尺度模型假设在一个代表性体积单元（REV）内，固体相与孔隙相的分布是均匀的，并采用连续的平均量来表征电化学特性，例如电导率、扩散系数以及三相界面（TPB）密度等 [384,385]。此外，对于传输过程，连续模型需要对有效电导率和有效扩散系数进行精确估算，而这些量与结构参数（如曲折度和体积分数）密切相关。然而，这些参数通常是通过间接方式获得的，要么来源于二维的扫描电子显微镜（SEM）或透射电子显微镜（TEM）图像，要么依据与其他测量结果的经验关联式推算得出 [371,386–388]。尽管这些方法在一定程度上简化了参数计算，但却忽略了不同相之间的三维细节连通性 [389,390]，从而导致连续尺度模型中存在较大的不确定性。

7.2.2 结构变形预测

为了获得致密化的电解质和电极微结构，固体氧化物燃料电池（SOFC）的相关材料必须经历多次高温烧结步骤，这一过程称为烧结过程（sintering process），并且与电池性能密切相关 [406]。诸如动力学蒙特卡罗（Kinetic Monte Carlo, KMC）、分子动力学（MD）以及离散元方法（DEM）等模型都可用于模拟烧结过程。KMC 方法因其能够处理相对较大的计算体积且编程实现相对简单而备受关注 [407,408]。

7.3 挑战

在固体氧化物燃料电池（SOFC）领域，孔隙尺度模型在预测电化学特性、寻找最优微结构以及研究电极劣化机理方面起着关键作用。然而，应用于 SOFC 的孔隙尺度模型仍面临若干挑战。为了实现对电化学性能的精确预测，需要能够重建高分辨率结构的方法。目前的 FIB-SEM 技术可以获得分辨率为数纳米级的三维结构，但随着计算精度要求的提高，最先进的三维重建技术的分辨率仍然不足。
此外，在 SOFC 的运行过程中，电化学反应通常涉及多个电化学步骤：气体组分的吸附、气体原子在电极表面的传输、氧化物离子的迁移，以及在三相界面（TPB）或双相界面（DPB）处的电化学反应 [414]。在现有的孔隙尺度模型中，为了减轻计算负担，通常只求解其中有限的几个过程，而忽略其他过程。因此，为了进一步提高计算精度，需要开发能够同时处理多种电化学过程的更先进数值模型。
此外，近年来的研究表明，电极的劣化与不同相在运行过程中的迁移密切相关 [415]。虽然相场法等孔隙尺度方法已被用于模拟这一现象，但目前仍缺乏能够与实验观测结果相匹配的高精度数值模型。

8 挑战与前景

尽管孔隙尺度建模在理解多孔介质中的传输过程方面发挥着越来越重要的作用，但我们希望就孔隙尺度建模的若干方面提出一些看法。

（1）在已有文献中，大量孔隙尺度建模工作的目标是预测连续尺度模型所需的宏观传输性质。当孔隙尺度建模用于此目的时，必须确保达到代表性体积单元（REV）条件。一方面，在某些情况下，孔隙尺度模型与连续尺度模型之间存在显著的尺度差距。**如何将特定多孔样品的孔隙尺度模拟结果有效地引入到更大尺度的连续尺度模拟中，是一项具有挑战性的任务，需要采用合适的上尺度方法 [416]。**另一方面，对于某些多孔介质而言，REV 实际上并不存在，例如厚度与典型孔径相当的薄层多孔介质 [332]。在这种情况下，将基于 REV 的孔隙尺度预测宏观传输性质直接用于连续尺度模型时，应当保持谨慎。

然而，孔隙尺度建模不能仅被视为改进连续尺度模型的工具。其更为重要的作用在于：揭示不同传输过程的内在物理机制，阐明多孔结构与孔隙尺度传输过程之间的相互作用，并为多孔介质在纳米/微米尺度上的结构优化设计提供指导。特别是，随着新一代纳米/微米制造技术的发展，已经逐渐能够制造具有特定纳米或微观结构及成分分布的多孔介质。孔隙尺度建模是回答“何种多孔结构和成分分布有助于提升性能”这一问题的天然选择 [417]，因此有望对下一代多孔介质的设计与开发产生前所未有的影响。

（2）精确的孔隙尺度建模依赖于高效的三维重建技术。对于结构重建而言，一个主要障碍在于三维微结构的分辨率较低。目前的 FIB-SEM 可视化技术能够获得分辨率约为 2 nm 的三维结构 [376]，然而，由于在多个研究领域（例如质子交换膜燃料电池的催化层 CL）中存在尺寸极小的反应性纳米颗粒，当前最先进的三维重建微结构的分辨率仍然不足。利用深度学习来提高三维微结构的分辨率是一种可行的解决方案 [418]。在过去几年中，已有多项研究尝试通过神经网络来提升三维结构的分辨率 [419,420]。然而，这种方法尚未真正应用于多孔介质的微结构几何重建。因此，仍需进一步研究以将神经网络技术用于提升三维多孔微结构的分辨率。另一种解决途径是开发能够获得亚纳米级分辨率三维结构的新技术。近年来，一些新方法如原子探针断层扫描atom probe tomography已被提出 [421]，借助这些技术可以实现亚纳米级的三维重建。然而，这些技术目前仍局限于少数应用领域，尚需进一步推广至其他研究方向。

（3）由于多孔结构在孔隙尺度建模中被直接解析，模拟通常需要极其庞大的数值网格；此外，如果为了包含更多几何细节而进一步提高分辨率，网格点数量将急剧增加。因此，在不牺牲计算精度的前提下降低计算负担成为当前模拟中迫切需要解决的问题。
为节省孔隙尺度建模的计算资源，研究者提出了多种不同的方案。例如，标准的格子 Boltzmann（LB）孔隙尺度建模需要在流体相和固体相中都存储粒子分布函数（PDFs）。然而，如果研究仅关注孔隙内部的传输过程，这种做法会造成计算资源浪费。为此，有学者提出了一种仅在孔隙单元中存储单组 PDFs 的方案，该方法对低孔隙率的多孔介质尤为高效 [422]。此外，还提出了一种多尺度分解（multiscale-decomposition）方案以加速孔隙尺度建模 [423]。在该方案中，物理变量被分解为体积平均项（代表长波长的全局变化）与相对于平均值的偏差项（代表局部波动）。首先利用三对角矩阵算法（TDMA）等方法求解体积平均项，然后基于此进行孔隙尺度建模。该方法能够在不降低精度的情况下显著减少计算成本。
除此之外，机器学习方法也被引入孔隙尺度建模，用于加速多孔介质传输特性的预测 [424,425]。在这种方案中，首先进行孔隙尺度建模以构建数据库，用于训练机器学习模型，如支持向量回归（SVR）、高斯过程回归（GPR）和卷积神经网络（CNN）；随后，利用训练好的模型实现多孔介质传输特性的快速预测。
此外，还提出了多尺度耦合建模方案，即在不同子区域采用不同的数值方法，从而在保留孔隙尺度细节的同时节省计算资源 [426,427]。例如，在包含自由流体区与多孔区的计算域中，分别采用有限体积法（FVM）与格子 Boltzmann 方法（LBM），并在两子域的界面处交换信息。
另外，Kishimoto 等人 [401,428] 提出了一种能够在粗网格中保留局部几何信息的数值模型，该方法在不牺牲计算精度的前提下，大幅减轻了计算负担。

（4）目前，孔隙尺度模型和数值方法仍需进一步完善。主要的挑战在于如何同时包含多种通常存在于不同多孔组分中的物理过程。以质子交换膜燃料电池（PEMFC）的催化层（CL）为例，氧还原反应（ORR）中氧气、质子和电子发生反应生成水。随后，在 CL 的纳米尺度结构中会出现复杂的水生成、吸附、蒸发/冷凝以及迁移等过程。然而，目前大多数孔隙尺度建模仍主要集中在等温单相反应传输过程上。尽管近年来孔隙尺度建模在揭示孔隙–离聚物界面现象及其在低铂负载条件下对电池性能的影响方面取得了重要进展 [78]，但仍迫切需要能够同时考虑质量传输、热传递、电化学反应与多相流动耦合机制的孔隙尺度模型。
此外，在催化层中，由于铂颗粒团聚、铂溶解以及碳基体塌陷引起的孔隙结构演化会导致性能劣化，因此需要发展能够考虑结构演化与电化学过程耦合的孔隙尺度模型 [338]。
另一个例子是固体氧化物燃料电池（SOFC）。其电极运行过程涉及气体的表面吸附、化学反应、气体传输以及离子传输等多种过程。然而，在当前最先进的孔隙尺度模拟中，这些过程通常被简化为一到两个步骤，从而显著降低了计算精度。未来的研究中，亟需在孔隙尺度模拟中显式地同时引入这些多种物理过程，以实现对实际传输与反应行为的更准确描述。

（5）将孔隙尺度建模与拓扑优化等优化技术相结合，可以用于指导多孔介质的设计。在给定一组特定目标和约束条件的情况下，基于数学最优理论的拓扑优化方法能够获得性能更优（例如传输性能更好）的优化结构。在优化迭代过程中，待优化结构内部的传输过程通常通过孔隙尺度模型求解，而拓扑优化生成的结构由于通常包含弯曲复杂的通道和界面，因此可视为一种多孔介质。
近年来，基于孔隙尺度建模的传输过程拓扑优化研究受到越来越多的关注，并被广泛应用于换热器和多孔电极等结构的优化设计 [405,429–433]。然而，目前拓扑优化的应用大多仍集中在单一物理过程或简单耦合过程上。此外，由于计算资源（如内存和 CPU 时间）的限制，大多数优化问题中的物理过程被简化为二维稳态过程。因此，为了将拓扑优化真正应用于实际工程设计，迫切需要基于孔隙尺度模型开发能够处理复杂耦合传输过程的优化模型，并发展适用于大规模并行计算的优化算法，从而解决三维非稳态过程的实际优化问题。

9 结论

通过本综述可以得出以下结论：孔隙尺度模拟在多个方面发挥着重要作用。

• 它能够提供物理、化学、电学以及生物过程的微观细节，极大地促进对孔隙尺度传输现象及不同过程之间复杂相互作用的理解，而这些信息往往是当前实验技术难以获取的。因此，孔隙尺度模型能够深入揭示宏观参数为何会呈现特定行为的内在机理。
• 孔隙尺度模拟可以揭示不同组分的微观结构与界面特性对反应传输过程的影响，这在研究非均质性效应（例如混合润湿性、局部缺陷、层级多孔结构等）时尤为重要。
• 通过采用上尺度方法，可以基于孔隙尺度模拟结果获得连续尺度模型所需的宏观有效传输性质。
• 基于对真实结构与孔隙尺度反应传输过程之间相互作用的理解，可以有针对性地调控多孔介质的结构与表面特性，从而强化、削弱、控制或调节相应的传输过程，最终提升多孔介质的整体性能。

总之，复杂的结构与多种耦合过程使多孔介质内部呈现出高度混乱的特性。孔隙尺度建模是一种能够从这种混沌中提炼出规律的强大工具。它不仅有助于设计性能更优的多孔介质，而且当其与纳米/微米尺度的制造技术（例如三维打印技术、软模板法、硬模板法等 [436–438]）相结合时，将推动新一代多孔介质的诞生。