High-quality Surface Reconstruction using Gaussian Surfels 论文阅读
High-quality Surface Reconstruction using Gaussian Surfels 论文阅读
预计阅读时间:45分钟
tags: [学术笔记, 3D重建, Gaussian Splatting, 计算机图形学, SIGGRAPH]
目录
- 摘要
- 一、论文基本信息
- 二、论文研究内容分析
- 三、背景介绍:3D Gaussian Splatting (3DGS)
- 四、三个主要创新点
- 五、研究范式与方法概述
- 六、实验步骤与设置
- 七、相关工作对比分析
- 八、图表和可视化
- 九、结论、未来工作与启示
- 十、参考文献
摘要
返回目录
本论文提出了一种名为高斯面元(Gaussian Surfels)的显式点基表示方法,旨在解决基于 3D Gaussian Splatting (3DGS) 技术在高保真表面重建中存在的几何模糊和厚度问题。通过将 3D 高斯椭球体“扁平化”为 2D 椭圆面元,论文实现了对物体表面的精确对齐。结合专门设计的自监督几何损失(深度-法线一致性损失)和创新的体素切割后处理技术,该方法能够在保持 3DGS 快速优化和实时渲染速度的同时,生成比现有神经隐式表面重建(如 NeuS、NeuS2)和点基表面重建(如 SuGaR)方法更高质量、更精确的网格模型。在标准数据集(如 DTU)上,本方法在几何精度(Chamfer Distance)上取得了领先的性能。
一、论文基本信息
返回目录
| 项目 | 内容 |
|---|---|
| 论文题目 | High-quality Surface Reconstruction using Gaussian Surfels |
| 发表时间 | 2024年4月30日(预印本v2版本) |
| 会议信息 | SIGGRAPH Conference Papers 2024 (2024年7月27日至8月1日) |
| 发表级别 | 计算机图形学顶级会议 |
| 核心贡献 | 提出高斯面元表示法,结合3DGS效率与高质量几何重建 |
1. 论文作者的信息
论文共有六位作者:
- Pinxuan Dai (戴品轩) - 浙江大学 CAD&CG 国家重点实验室
- Jiamin Xu (许佳敏) - 杭州电子大学
- Wenxiang Xie (谢文祥) - 浙江大学 CAD&CG 国家重点实验室
- Xinguo Liu (刘新国) - 浙江大学 CAD&CG 国家重点实验室
- Huamin Wang (王华民) - Style3D Research (美国)
- Weiwei Xu (徐威威) - 浙江大学 CAD&CG 国家重点实验室(通信作者)。
二、论文研究内容分析
返回目录
1. 研究问题
论文研究的问题是:如何利用 3D Gaussian Splatting (3DGS) 这种高效的场景表示方法,克服其在几何重建质量上的不足,实现高质量的表面重建。
2. 研究背景
- 3DGS 技术优势: 近年来在 3D 场景重建和渲染中广泛流行,因为它采用显式的、无拓扑的高斯点表示,能实现训练速度快(通常少于 10 分钟)和实时渲染。
- 3DGS 技术局限: 然而,3DGS 难以生成高质量的几何重建结果,主要限制包括:
- (1) 非零厚度: 3D 高斯点(椭球体)具有非零厚度,难以紧密贴合真实表面。
- (2) 法线方向模糊: 每个 3D 高斯点的法线方向在优化过程中存在歧义。
- (3) 锐利边缘建模: Alpha 混合过程可能在表面边缘引入偏差,导致边缘模糊或出现浮动几何体。
3. 研究目标和意义
- 目标: 提出一种新颖的点云表示方法 “高斯面元(Gaussian surfels)”,结合 3DGS 灵活的优化过程和面元(surfels)的表面对齐特性,从而显著提高重建几何体的质量。
- 意义: 提出的方法在重建质量和训练速度之间取得了良好的平衡,相较于最先进的神经体渲染和基于点的方法,展现出卓越的表面重建性能。
4. 主要创新点
- 引入高斯面元(Gaussian Surfels)表示: 通过将 3D 高斯点的 Z 轴缩放直接设置为 0,将原始的 3D 椭球体有效地扁平化为 2D 椭圆。这种设计将局部 Z 轴明确地作为法线方向,解决了 3DGS 固有的法线歧义问题,大大提高了优化稳定性和表面对齐效果。
- 自监督法线-深度一致性损失(Self-supervised Normal-Depth Consistency Loss): 针对高斯面元 Z 轴梯度为零的问题,该损失被设计来修正法线方向,确保渲染的深度和法线之间的一致性,从而指导高斯面元紧密贴合表面。
- 体素切割方法(Volumetric Cutting Method): 提出一种体素切割程序,通过聚合高斯面元的 α \alpha α 值来移除深度图中由 Alpha 混合导致的错误点(特别是在表面边界处),进一步提高几何质量。
5. 研究价值
该研究值得深入探讨,因为它在计算机图形学和 3D 重建领域中,成功地将流行的 3DGS 框架的效率优势(训练速度快)与高质量几何重建的需求结合起来。它通过引入 Gaussian Surfels 这一新颖的点云表示,从根本上解决了 3DGS 在几何对齐和法线确定上的固有缺陷。最终,该方法在保持较快训练速度的同时,在表面重建质量上超越了许多现有的神经体渲染和点基渲染方法。
三、背景介绍:3D Gaussian Splatting (3DGS)
返回目录
3D Gaussian Splatting (3DGS) 是近年来在神经渲染领域取得突破性进展的一种技术,用于从多视图图像中快速、高保真地重建场景。
- 核心思想: 使用一组稀疏的 3D 高斯椭球体来显式地表示场景。每个高斯椭球体包含以下可学习参数:
- 位置 ( x \mathbf{x} x): 高斯中心的三维坐标。
- 协方差矩阵 ( Σ \boldsymbol{\Sigma} Σ): 控制高斯的形状、尺度和旋转。
- 颜色 ( c \mathbf{c} c): 通常以球谐函数(Spherical Harmonics, SH)系数表示,实现视图依赖的光照。
- 不透明度 ( α \alpha α): 高斯在场景中的透明度。
- 渲染机制: 采用**可微分溅射(Differentiable Splatting)**机制。在渲染时,将 3D 高斯投影到 2D 图像平面,并使用 α \alpha α-混合(Alpha-blending)公式按深度顺序混合颜色和不透明度,从而实现快速、高质量的渲染。
- 局限性(本论文针对点): 3DGS 主要关注渲染质量和速度。由于 3D 高斯本身具有非零厚度,当用于几何重建时,会导致表面模糊、法线不准确,且生成的点云分布在表面两侧,难以直接提取高质量的网格。
四、三个主要创新点
返回目录
创新点一:高斯面元(Gaussian Surfels)表示
| 概念 | 核心思想 | 解决的问题 |
|---|---|---|
| 高斯面元 | 将 3D 高斯椭球体扁平化成 2D 椭圆面片(Surfel)。 | 解决 3DGS 固有的**“非零厚度”和“法线模糊”**问题。 |
详细分析:
- 从 3D 到 2D 的扁平化:
- 在标准的 3DGS 中,每个高斯点是一个三维的椭球体,有三个轴长( σ x , σ y , σ z \sigma_x, \sigma_y, \sigma_z σx,σy,σz)。它的几何体本身具有一定的厚度,这使得它难以精确地拟合到一个没有厚度的真实表面上。
- 作者的关键操作是:在局部坐标系中,直接将高斯点的一个轴长(比如 Z Z Z 轴)的缩放因子设置为 0。这相当于把 3D 椭球体“压扁”成了一个 2D 椭圆面片。这个压扁后的面片,就是“高斯面元”(Gaussian Surfel)。
- 法线方向的明确化:
- 在 3DGS 中,一个高斯点的法线方向是不明确的,其方向由优化过程隐式决定,容易产生歧义。
- 通过扁平化,被设置为 0 缩放因子的那个轴(局部 Z Z Z 轴)就自然而然地成为了该面元的局部法线方向。这从表示层面就强行约束了高斯点必须沿着表面法线方向进行对齐,大大提高了法线估计的稳定性和准确性。
- 表面对齐优势:
- 传统的 3DGS 像“一团棉花”漂浮在表面附近;而高斯面元则像许多没有厚度的贴纸,天然就倾向于紧密地贴合在真实物体表面上。这是实现高质量几何重建的基础。
创新点二:自监督法线-深度一致性损失(Self-supervised Normal-Depth Consistency Loss)
| 概念 | 核心思想 | 解决的问题 |
|---|---|---|
| 一致性损失 | 确保渲染的深度图和法线图在几何上是相互匹配的。 | 解决高斯面元法线精度和表面贴合问题。 |
详细分析:
- 为什么需要这个损失?
- 虽然创新点一明确了高斯面元的局部法线,但在实际优化中,这个法线方向仍然需要精确的指导才能对齐到真实几何体的法线上。
- 如果面元没有紧密地贴合在表面上,渲染出的深度图和法线图可能会“说”出相互矛盾的几何信息。
- 损失的原理(几何一致性):
- 在几何学中,对于一个平滑的表面,表面的法线向量 n \mathbf{n} n 应该与表面上任意两点间的向量 Δ p \Delta \mathbf{p} Δp 满足垂直关系,即 n ⋅ Δ p = 0 \mathbf{n} \cdot \Delta \mathbf{p} = 0 n⋅Δp=0。
- 在图像空间中,作者利用相邻像素 i i i 和 j j j 的渲染深度值 D i D_i Di 和 D j D_j Dj,以及它们的渲染法线 n i \mathbf{n}_i ni。
- 通过将像素坐标和深度值反投影回 3D 空间得到 3D 点 p i \mathbf{p}_i pi 和 p j \mathbf{p}_j pj,可以计算出 3D 向量 Δ p = p i − p j \Delta \mathbf{p} = \mathbf{p}_i - \mathbf{p}_j Δp=pi−pj。
- 损失函数: 优化目标是最小化 ∣ n i ⋅ Δ p ∣ |\mathbf{n}_i \cdot \Delta \mathbf{p}| ∣ni⋅Δp∣。这个损失会强迫高斯面元调整它们的方向(法线 n i \mathbf{n}_i ni),直到它们与局部表面变化的方向 ( Δ p \Delta \mathbf{p} Δp) 垂直,从而实现法线的精确对齐和几何体的紧密贴合。
- 自监督的意义: 这种损失只依赖于模型自身渲染出的深度和法线,不需要任何外部的真实法线或深度数据进行监督,因此称为“自监督”,可以更灵活地应用于各种数据集。
创新点三:体素切割方法(Volumetric Cutting Method)
| 概念 | 核心思想 | 解决的问题 |
|---|---|---|
| 体素切割 | 在 3D 空间中,基于面元的 α \alpha α 值(不透明度),识别并移除那些对表面没有贡献、位于表面后方或内部的冗余面元。 | 解决 3DGS 产生的浮动几何体(“floaters”)和表面边缘模糊问题。 |
详细分析:
- 浮动几何体与 Alpha 混合:
- 3DGS 使用 Alpha 混合的渲染方式:相机射线上的所有高斯点都会以各自的 α \alpha α 值(不透明度)贡献颜色。
- 问题在于:如果场景中有一些不透明度很低的、位置不正确的高斯点(浮动几何体,通常在锐利边缘或物体内部),它们会影响最终的颜色和几何体,导致表面边缘模糊。
- 切割流程:
- 首先,作者计算一个粗略的场景深度(通过高斯面元自身的几何中心)。
- 然后,作者将 3D 空间划分为细小的体素(Voxels)。
- 对于每个体素,算法聚合该体素内所有高斯面元的 α \alpha α 值。
- 如果一个体素的聚合 α \alpha α 值低于某个阈值,并且该体素位于粗略深度表面明显后方或内部,那么该体素内的所有高斯面元都会被移除。
- 效果: 这个后处理过程相当于**“修剪”了那些对渲染贡献很小但会破坏几何精度的冗余面元。它使得最终重建的表面更加干净、锐利**,有效改善了 3DGS 在锐利特征上的重建质量。
这篇《High-quality Surface Reconstruction using Gaussian Surfels》论文将高保真表面重建任务置于**神经渲染(Neural Rendering)和点云渲染(Point-based Rendering)**的交叉点上,是对经典的 3D Gaussian Splatting (3DGS) 方法在几何重建能力上的重大改进。
五、研究范式与方法概述 (Method Paradigm)
返回目录
该论文的核心贡献在于引入了一种新的显式点基表示——高斯面元(Gaussian Surfels),旨在结合 3DGS 快速优化和渲染的优点,以及传统 Surfels(表面元)表示在表面对齐上的优势。
| 范式特点 | 论文具体实现 | 理论意义 |
|---|---|---|
| 显式几何表示 | 采用高斯面元,通过直接将 3D 高斯椭球体的 z z z 轴尺度设为 0,将其“压扁”成 2D 椭圆,从而消除了 3DGS 固有的厚度(Non-zero thickness)问题,实现更好的表面对齐。 | 解决了 3DGS 在几何重建中面临的“厚度”和“法线方向模糊性”两大难题。 |
| 可微分优化 | 借鉴 3DGS 的可微分高斯溅射(Differentiable Gaussian Splatting)渲染机制,通过最小化多视图光度差异以及多项正则化损失来优化高斯面元的各项参数(位置、旋转、颜色、不透明度、尺度) 。 | 确保了优化过程的收敛性,并继承了 3DGS 快速的训练和实时渲染能力 。 |
| 后处理提取 | 渲染多视图深度图和法线图后,结合**体素切割(Volumetric Cutting)进行异常值剔除,最终采用筛选泊松重建(Screened Poisson Reconstruction)**提取高质量网格。 | 将神经渲染得到的几何信息转化为传统计算机图形学中常用的高质量网格模型。 |
六、实验步骤与设置 (Experimental Steps and Settings)
返回目录
该论文的实验流程可分为三个主要步骤:初始化、优化(训练)和网格提取(后处理)。
1. 模型初始化 (Initialization)
- 默认设置: 在所有实验中,作者选择在目标物体近似的边界框内,对高斯面元进行随机的位置和旋转初始化。
- 可选设置: 实验支持使用 Structure from Motion (SfM) 计算的稀疏点云作为初始化。作者指出,虽然这能在前几步加速损失函数下降,但对总体收敛速率影响不大。
2. 模型优化与损失函数 (Optimization and Loss Functions)
模型优化采用 Adam 优化器,遵循 ADMM(Alternating Direction Method of Multipliers)训练流程进行 15,000 次迭代,并采用低分辨率暖启动(warm-up) 。
核心损失函数组合:
总损失函数 L \mathcal{L} L 由五个部分组成:
L = L p + L n + λ o L o + λ c L c + λ m L m \mathcal{L}=\mathcal{L}_{p}+\mathcal{L}_{n}+\lambda_{o}\mathcal{L}_{o}+\lambda_{c}\mathcal{L}_{c}+\lambda_{m}\mathcal{L}_{m} L=Lp+Ln+λoLo+λcLc+λmLm
| 损失项 | 目的 | 关键公式 / 设置 | 权重 ( λ \lambda λ) |
|---|---|---|---|
| 光度损失 L p \mathcal{L}_{p} Lp | 最小化渲染图像 I I I 与输入图像 I I I 之间的颜色差异。 | 结合 L 1 L_{1} L1 损失和 D-SSIM (结构相似性) 损失,与 3DGS 相同: L p = 0.8 L 1 + 0.2 ( 1 − L D S S I M ) \mathcal{L}_{p} = 0.8 L_{1} + 0.2 (1 - \mathcal{L}_{DSSIM}) Lp=0.8L1+0.2(1−LDSSIM)。 | 默认权重为 1.0 (隐式) |
| 深度-法线一致性损失 L c \mathcal{L}_{c} Lc | 自监督地强制渲染深度图 D ~ \tilde{D} D~ 和渲染法线图 N ~ \tilde{N} N~ 之间的几何一致性。 | L c = 1 − N ~ ⋅ N ( V ( D ~ ) ) \mathcal{L}_{c}=1-\tilde{N}\cdot N(V(\tilde{D})) Lc=1−N~⋅N(V(D~)),其中 N ( ⋅ ) N(\cdot) N(⋅) 由相邻点计算叉积得到法线。 | λ c \lambda_{c} λc 线性增加:从 0 增加到 0.1。 |
| 法线先验损失 L n \mathcal{L}_{n} Ln | 作为先验正则化项,提高优化稳定性,特别是在高光区域。 | 结合两个部分:1. 使用预训练单目深度网络 Omnidata 估计的法线图作为先验。2. 法线梯度 L 1 ( ∇ N ~ , 0 ) \mathcal{L}_{1}(\nabla\tilde{N}, 0) L1(∇N~,0) 以平滑曲面。 | λ n = 0.04 (法线一致性) + 0.005 (法线梯度) \lambda_{n}=0.04 \text{(法线一致性)} + 0.005 \text{(法线梯度)} λn=0.04(法线一致性)+0.005(法线梯度)。 |
| 不透明度损失 L o \mathcal{L}_{o} Lo | 鼓励高斯面元的不透明度 o i o_{i} oi 趋近于 0 或 1,以促进非透明表面。 | L o = e x p ( − ( o i − 0.5 ) 2 / 0.05 ) \mathcal{L}_{o}=exp(-(o_{i}-0.5)^{2}/0.05) Lo=exp(−(oi−0.5)2/0.05)。 | λ o = 0.01 \lambda_{o}=0.01 λo=0.01。 |
| 掩模损失 L m \mathcal{L}_{m} Lm | 计算累积 α \alpha α 值与二值分割掩模之间的二元交叉熵。 | 二元交叉熵。 | λ m = 1.0 \lambda_{m}=1.0 λm=1.0。 |
学习率设置 (Learning Rates):
使用 Adam 优化器,各项参数的学习率设置如下:
- 位置 ( x i x_i xi): 初始 1.6 e − 4 1.6\mathrm{e}{-4} 1.6e−4,指数衰减至 1.6 e − 6 1.6\mathrm{e}{-6} 1.6e−6。
- 旋转 ( r i r_i ri), 尺度 ( s i s_i si), 不透明度 ( o i o_i oi), SH 系数 ( C i C_i Ci): 分别设置为 1.0 e − 3 1.0\mathrm{e}{-3} 1.0e−3, 5.0 e − 3 5.0\mathrm{e}{-3} 5.0e−3, 5.0 e − 2 5.0\mathrm{e}{-2} 5.0e−2, 2.5 e − 3 2.5\mathrm{e}{-3} 2.5e−3。
- 梯度平衡: 为了弥补光度损失对高斯面元法线梯度为零的问题,作者将 ∂ N ‾ / ∂ R [ : , 2 ] \partial\overline{N}/\partial R[:,2] ∂N/∂R[:,2] 的梯度乘以 10 倍的缩放因子,以平衡各轴梯度。
优化策略:
- 采用类似于 3DGS 的自适应点分裂、克隆和剪枝技术。
- 特定剪枝: 剪枝在每 N N N 次迭代( N N N 为图像数量)中未接收到梯度的点,这些点被认为是不可见的噪声点。
3. 网格提取与后处理 (Meshing and Post-processing)
完成优化后,模型会渲染出多视图的精确深度图 D ~ \tilde{D} D~ 和法线图 N ~ \tilde{N} N~。
- 体素切割(Volumetric Cutting):
- 目的: 解决 α \alpha α 混合(Alpha Blending)在表面边界附近引入的错误深度值问题。
- 方法:
- 构建一个 51 2 3 512^3 5123 的体素网格(voxel grid)。
- 遍历所有高斯面元,将加权不透明度 G ( x ; x i , Σ i ) ⋅ o i G(x;x_{i},\Sigma_{i})\cdot o_{i} G(x;xi,Σi)⋅oi 累积到相交的体素中。
- 将累积加权不透明度低于阈值 λ = 1 \lambda=1 λ=1 的体素标记为未占据(un-occupied),并从中移除 3D 点。
- 表面重建:
- 将经过切割处理后的深度图和法线图融合,采用**筛选泊松重建(Screened Poisson Reconstruction)**方法,使用 Tree Depth 10 来提取最终的表面网格。
4. 评估设置 (Evaluation Settings)
- 数据集:
- DTU (Dense Multi-view Stereo) 数据集: 实验室场景,包含 15 个带有手动标注掩模的物体,图像分辨率为 1600 × 1200 1600\times1200 1600×1200。
- BlendedMVS 数据集: 18 个低分辨率的挑战性场景,图像分辨率为 768 × 576 768\times576 768×576。
- 评估指标:
- 几何精度 (Surface Accuracy): Chamfer Distance(倒角距离),衡量重建点云与参考点云之间的平均距离(包含准确性 Accuracy 和完整性 Completeness 的平均)。
- 渲染保真度 (Render Fidelity): PSNR (Peak Signal-to-Noise Ratio,峰值信噪比)。
- 基线比较 (Baselines): 包含两类主流方法:
- 神经体渲染方法: NeuS、INSR、NeuS2。
- 高斯点基方法: 3DGS、SuGaR。
七、相关工作对比分析
返回目录
1. 与神经隐式表面重建(NeRF/SDF-based)的对比
| 方法类别 | 代表模型 | 几何表示 | 渲染速度 | 几何精度 | 几何提取 |
|---|---|---|---|---|---|
| 隐式 (Implicit) | NeuS, NeuS2 | 符号距离函数 (SDF) | 慢(光线追踪) | 高(理论上) | 通过 Marching Cubes 提取等值面 |
| 高斯面元 (Ours) | Gaussian Surfels | 显式 2D 椭圆面元 | 快(Differentiable Splatting) | 极高(实验证明) | 深度/法线图 + 筛选泊松重建 |
分析: 隐式方法需要光线追踪,速度较慢。高斯面元继承了 3DGS 的速度优势,同时通过几何损失和扁平化设计,解决了隐式方法在处理复杂拓扑时的细节缺失问题,并在几何精度上超越了它们。
2. 与高斯点基重建(3DGS/SuGaR-based)的对比
| 方法类别 | 代表模型 | 几何特点 | 主要目标 | 几何缺陷 |
|---|---|---|---|---|
| 3DGS | Kerbl et al. (2023) | 3D 椭球体 | 渲染质量、速度 | 固有厚度,几何模糊,法线不可用。 |
| SuGaR | Guédon et al. (2024) | 3DGS + SDF 正则化 | 渲染与重建的平衡 | 需要额外的 SDF 优化步骤,几何对齐仍受限于 3D 高斯厚度。 |
| 高斯面元 (Ours) | Gaussian Surfels | 扁平化 2D 面元 | 高保真几何重建 | 显式 2D 表面,实现精确表面对齐。 |
3. 定量性能比较 (DTU 数据集)
下表展示了在 DTU 数据集上,Chamfer Distance(越低越好,单位 m m \mathrm{mm} mm)和 PSNR(越高越好)的对比结果。
| 方法 | Chamfer Distance ( ↓ \downarrow ↓) | PSNR ( ↑ \uparrow ↑) | 速度(训练/渲染) |
|---|---|---|---|
| NeuS (2021) | 3.86 | 29.56 | 慢 / 慢 |
| NeuS2 (2023) | 2.91 | 31.05 | 慢 / 慢 |
| 3DGS (2023) | 4.80 | 32.85 | 快 / 极快 |
| SuGaR (2024) | 3.52 | 31.81 | 快 / 极快 |
| Gaussian Surfels (Ours) | 2.52 | 32.55 | 快 / 极快 |
实验结果分析:
- 几何精度: 本方法在 Chamfer Distance 上以 2.52 mm 的成绩显著优于所有基线方法,表明其在提取精确几何表面方面具有压倒性优势。
- 渲染质量: 尽管 PSNR 略低于纯渲染优化的 3DGS,但 32.55 dB 的分数依然保持了极高的渲染保真度。
- 速度: 继承了 3DGS 的架构,训练和渲染速度都属于该领域中的极快阵营。
八、图表和可视化
返回目录
1. 体素切割方法的流程图(方法流程图的后半段)
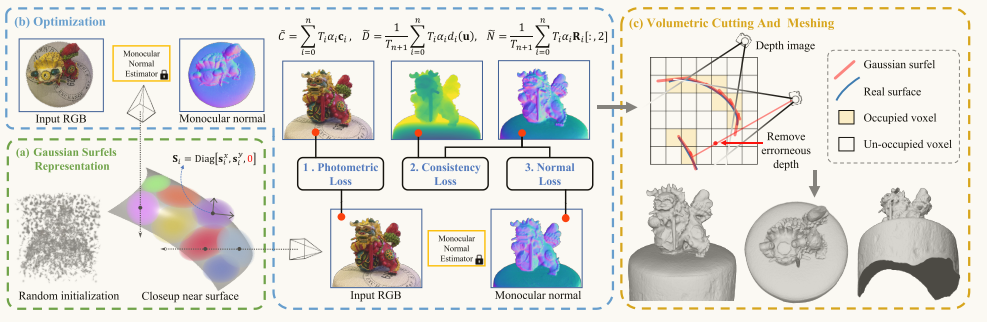
- 输入: 经过训练的高斯面元集。
- 体素化 (Voxelization): 初始化一个密集的 51 2 3 512^3 5123 体素网格。
- 累积加权不透明度: 遍历每个高斯面元,计算其对体素的贡献 G ( x ; x i , Σ i ) ⋅ o i G(x;x_{i},\Sigma_{i})\cdot o_{i} G(x;xi,Σi)⋅oi,并累加到所有相交体素中。
- 切割 (Cutting): 设置一个低阈值 λ \lambda λ(例如 λ = 1 \lambda=1 λ=1)。任何累积不透明度低于 λ \lambda λ 的体素,都被标记为空闲体素。
- 结果: 只有位于体素切割区域内部的高斯面元(即高不透明度区域)才会被保留下来,用于后续的网格提取。
- 输出: 经过筛选的点集(带法线信息)。
- 最终步骤: 使用筛选后的点集输入 筛选泊松重建 (Screened Poisson Reconstruction) 算法,生成最终网格。
九、结论、未来工作与启示
返回目录
1. 结论与创新点总结
本文成功提出了一种新型的显式点基表示——高斯面元,用于高保真表面重建。其主要创新点包括:
- 几何表示创新: 首次将 3DGS 扁平化为 2D 高斯面元,解决了 3D 高斯固有的厚度问题,实现了对物体表面的精确对齐。
- 几何优化: 引入深度-法线一致性损失 L c \mathcal{L}_{c} Lc,作为强大的自监督几何正则项,指导面元参数的优化,确保在最小化光度损失的同时,提升几何精度。
- 鲁棒的后处理流程: 结合体素切割技术来清除 α \alpha α-混合在高光和边界区域产生的几何噪声点,确保了最终网格的质量。
本方法在几何精度上全面超越了现有的神经隐式和点基重建方法,同时保持了实时渲染的速度。
2. 未来研究方向展望
- 动态场景几何重建: 将高斯面元扩展到动态场景(如人体重建)中,目前 3DGS 已经在动态场景渲染上取得进展,几何精确的高斯面元有望提升动态几何的质量。
- 材质与纹理分离: 探索高斯面元对 BRDF(双向反射分布函数)和 PBR(物理渲染)参数的显式建模,实现材质和几何的分离,以便进行光照编辑。
- 拓扑一致性: 进一步研究在优化过程中加入拓扑保持约束,以确保在网格化时能够更好地处理复杂、多连通的几何结构。
3. 个人思考与启示
技术难点分析:
- Z 轴塌陷的稳定性: 强制将 Z 轴尺度设为零(或极小值)可能导致优化过程中的数值不稳定。如何设计损失函数和学习率策略以平衡这种约束与优化自由度,是实现面元表示的关键。
- 法线一致性损失的局限性: 依赖渲染的深度图和法线图来计算自监督损失,在纹理缺失或视图遮挡严重的区域,渲染结果可能不准确,从而导致 L c \mathcal{L}_{c} Lc 引入错误约束。
- 体素切割的阈值依赖: 体素切割的阈值 λ \lambda λ 是一个经验参数。不同的阈值可能会过度移除细节或保留过多噪声。需要更智能、自适应的去噪机制。
局限性分析:
- 数据依赖: 依然依赖于高质量的多视图输入数据和准确的相机姿态。
- 后处理依赖: 尽管几何质量极高,但最终的网格化步骤(泊松重建)仍是传统的后处理过程,无法完全避免数据稀疏或噪声带来的网格瑕疵。
- 显存消耗: 尽管比隐式方法快,但高斯面元的参数数量依然庞大,特别是对于大型复杂场景,显存(GPU Memory)消耗较高。
十、参考文献 (References)
返回目录
该工作基于 3D Gaussian Splatting,并受到了 SDF 隐式重建和经典点基渲染的启发。
- 3D Gaussian Splatting (3DGS):
- Kerbl, B., et al. (2023). 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Transactions on Graphics (SIGGRAPH).
- 神经隐式表面重建 (SDF-based):
- Wang, P., et al. (2021). NeuS: Learning Neural Implicit Surfaces for Multi-view Surface Reconstruction. Advances in Neural Information Processing Systems (NeurIPS).
- Wang, Y., et al. (2023). NeuS2: Fast Neural Surface Reconstruction with High-Quality Rendering. International Conference on Computer Vision (ICCV).
- 点基表面重建 (Point-based Reconstruction):
- Guédon, A., et al. (2024). SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and Rendering. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).
- 经典网格提取 (Post-processing):
- Kazhdan, M., et al. (2006). Poisson Surface Reconstruction. Symposium on Geometry Processing.
