【Leetcode hot 100】70.爬楼梯
问题链接
70.爬楼梯
问题描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
提示:
1 <= n <= 45
问题解答
一、基础动态规划解法
思路分析
- 定义 dp 数组含义:设
dp[i]表示“爬到第 i 层楼梯的不同方法数”。 - 推导递推公式:
要爬到第 i 层,最后一步只有两种可能:- 从第 i-1 层再爬 1 个台阶(方法数 =
dp[i-1]); - 从第 i-2 层再爬 2 个台阶(方法数 =
dp[i-2])。
因此,总方法数为两者之和:dp[i] = dp[i-1] + dp[i-2]。
- 从第 i-1 层再爬 1 个台阶(方法数 =
- 初始化 dp 数组:
- 当
i=1时,只有 1 种方法(直接爬 1 阶),故dp[1] = 1; - 当
i=2时,有 2 种方法(1+1 或 2),故dp[2] = 2。
- 当
- 遍历顺序:从
i=3开始向前遍历(需先知道前两层的结果才能计算当前层)。
代码实现
class Solution {public int climbStairs(int n) {// 边界处理:n=1 或 n=2 时直接返回结果if (n <= 2) {return n;}// 定义 dp 数组,长度为 n+1(对应 0~n 层,0 层未使用)int[] dp = new int[n + 1];// 初始化前两层dp[1] = 1;dp[2] = 2;// 从第 3 层遍历到第 n 层for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}// 返回爬到第 n 层的方法数return dp[n];}
}
复杂度分析
- 时间复杂度:O(n),仅需遍历 1 次(从 3 到 n)。
- 空间复杂度:O(n),使用了长度为 n+1 的 dp 数组。
二、空间优化解法(最优效率)
思路分析
观察基础解法可知,计算 dp[i] 仅依赖前两个值(dp[i-1] 和 dp[i-2]),无需存储整个 dp 数组。因此,可使用 两个变量 替代数组,将空间复杂度优化至 O(1)。
- 用
prevPrev表示dp[i-2](前两层的方法数); - 用
prev表示dp[i-1](前一层的方法数); - 每次遍历计算当前层
curr = prev + prevPrev,再更新prevPrev和prev(滚动更新)。
代码实现
class Solution {public int climbStairs(int n) {// 边界处理:n=1 或 n=2 时直接返回结果if (n <= 2) {return n;}// 初始化:prevPrev = dp[1],prev = dp[2]int prevPrev = 1; // 爬到第 1 层的方法数int prev = 2; // 爬到第 2 层的方法数int curr = 0; // 存储当前层(i >=3)的方法数// 从第 3 层遍历到第 n 层for (int i = 3; i <= n; i++) {curr = prev + prevPrev; // 当前层 = 前一层 + 前两层prevPrev = prev; // 更新前两层(为下一次循环准备)prev = curr; // 更新前一层(为下一次循环准备)}// 返回爬到第 n 层的方法数return curr;}
}
复杂度分析
- 时间复杂度:O(n),遍历次数与基础解法一致。
- 空间复杂度:O(1),仅使用 3 个变量(无额外数组)。
三、特殊补充:数学公式法
本题本质是斐波那契数列的变形(斐波那契数列通常定义为 F(0)=0, F(1)=1, F(2)=1,本题从 F(1)=1, F(2)=2 开始),可直接使用斐波那契数列的通项公式计算:
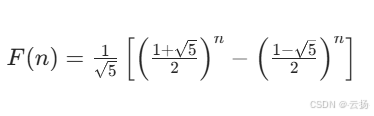
代码实现
class Solution {public int climbStairs(int n) {double sqrt5 = Math.sqrt(5);double fibN = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);return (int) (fibN / sqrt5);}
}
- 说明:该方法时间复杂度 O(1),但实际开发中较少使用(浮点数计算存在微小精度误差,且可读性差),面试中优先推荐动态规划解法。
总结
| 解法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 基础动态规划 | O(n) | O(n) | 初学者理解思路 |
| 空间优化版 | O(n) | O(1) | 面试推荐(效率最优) |
| 数学公式法 | O(1) | O(1) | 理论研究(实际用得少) |
