--- 数据结构 AVL树 ---

二叉搜索树： 他的右子树全小于根节点，左子树全部大于根节点

那么对于二叉搜索树在查询时时间复杂度就来到了惊人的 log(N) 这他大量数据下的查询基本就来到了常数级别，非常厉害的查询效率，但是在储存有序的数组时，会退化为单枝树，这时的平均查询效率来到了N/2  而最差会来到 N

那么为了避免这种情况，就可以使用AVL树，AVL时高度平衡的树， 左右子树高度差不会超过1，其高度可以保证在 log(N)，是完美的二叉搜索树

插入数据

使用二叉搜索树的方式插入数据，插入之后，二叉树的高度差平衡可能会受到破坏，而AVL树通过旋转子树来维持这个平衡

AVL树中有个平衡因子，用来判断左右子树直接的高度差，bf = 右子树高度 - 左子树高度

插入之后需要更新树的平衡因子，cur记录当前插入的点的，parent是cur的父结点，如果cur是parent的左节点，prent.bf--，否则是右节点，prent.bf++，之后parent和cur一起走到他们自己的父结点向上继续更新bf，如果更新之后patent.bf ＝0，更新完成，如果patent.bf ＝-2 或者 2，那么平衡被打破了那么就需要通过旋转这个平衡因子为2的节点来达到平衡状态

根据不同的插入位置，最终会有四种不平衡的情况

右单旋 当插入的位置是较高的左子树的左支

左支指的是40这个节点，不要在意插入的位置是40的左节点还是右节点

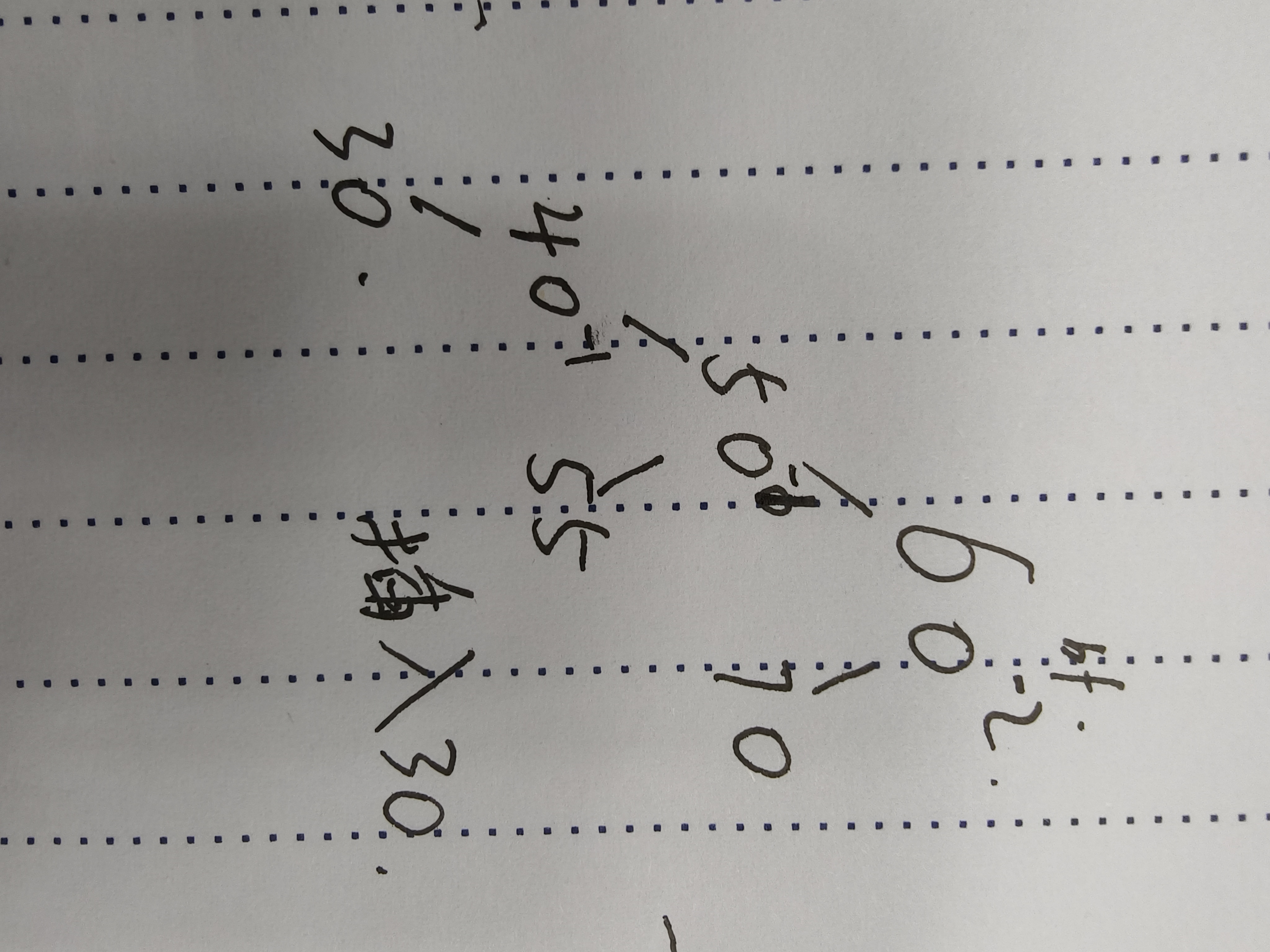
 60的高度不平衡，左边高了一层，那么就需要将60右旋降低高度

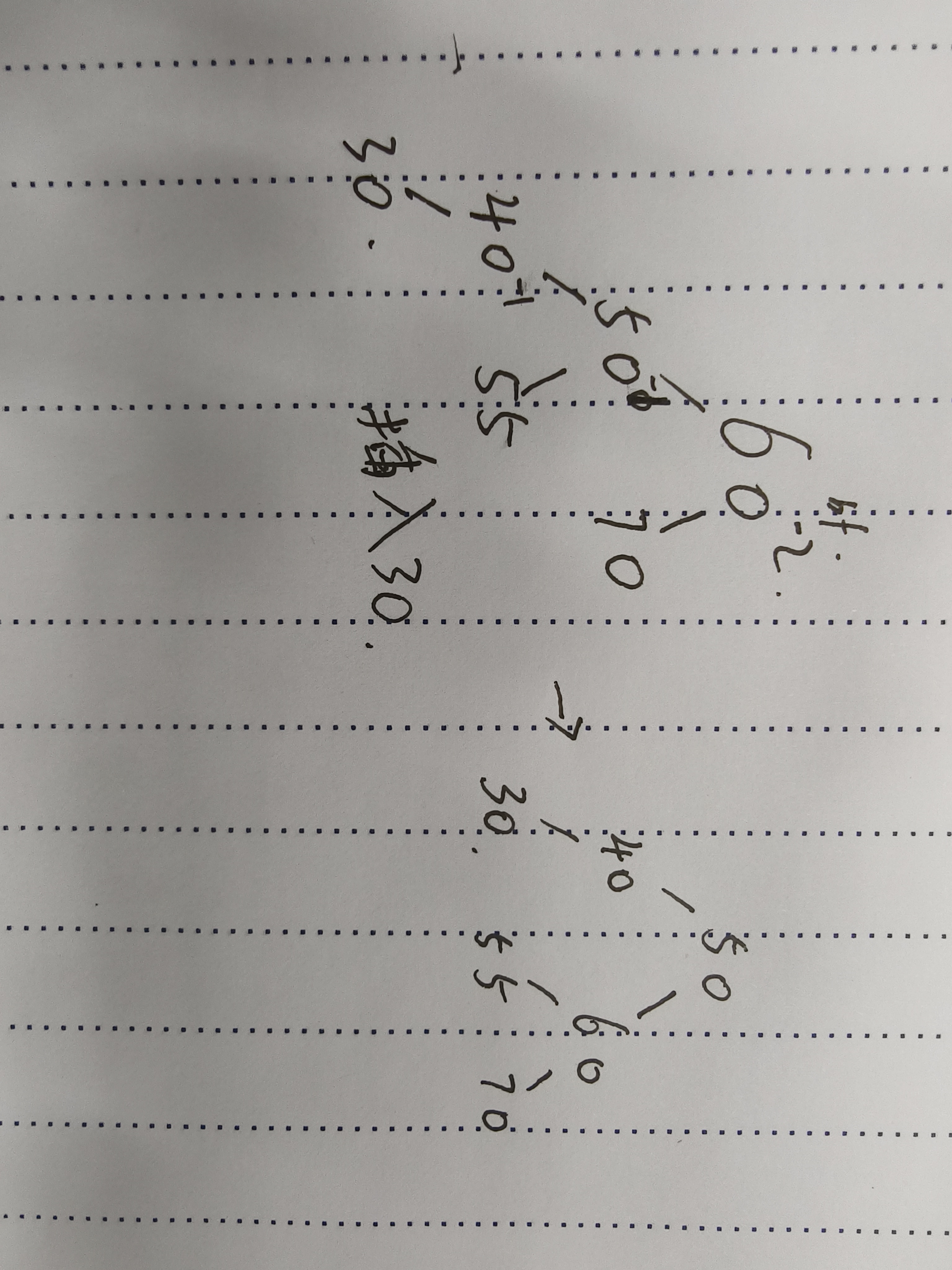
对60这个平衡因子为-2的节点进行右单旋，把60往右下移动，50右上移动来接替60的位置，而50有右节点而60没有父结点和左节点（60的左节点本来是50），那么吧50的右节点设置为60，然后把50的右结点接到60的左节点，且正好60的左节点满足小于60大于50，这正好满足拼接条件

 代码实现

private void rotateRight(Node parent) {Node subL = parent.left;Node subLR = subL.right;//旋转subL.right = parent;Node parentH = parent.parent;parent.parent = subL;parent.left = subLR;if (subLR != null) {subLR.parent = parent;}if (parent == root) {root = subL;subL.parent = null;} else {//parent不为根if (parentH.left == parent) {parentH.left = subL;subL.parent = parentH;} else {parentH.right = subL;subL.parent = parentH;}}subL.bf = 0;parent.bf = 0;}

对于特殊的单支不平衡树，也可以通过右单旋解决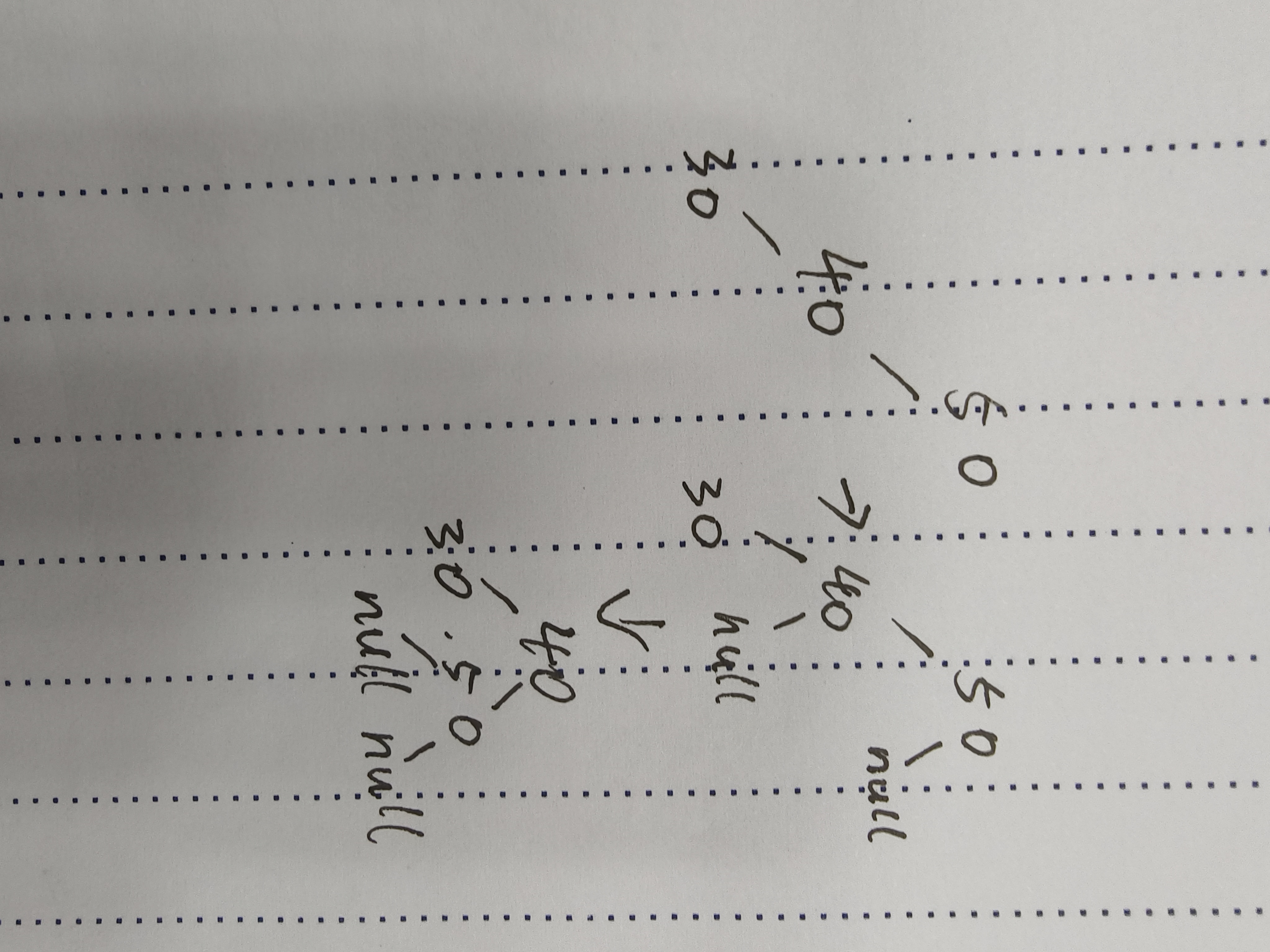

左单旋 插入的位置是较高的右子树右支

和左单旋的逻辑相同的

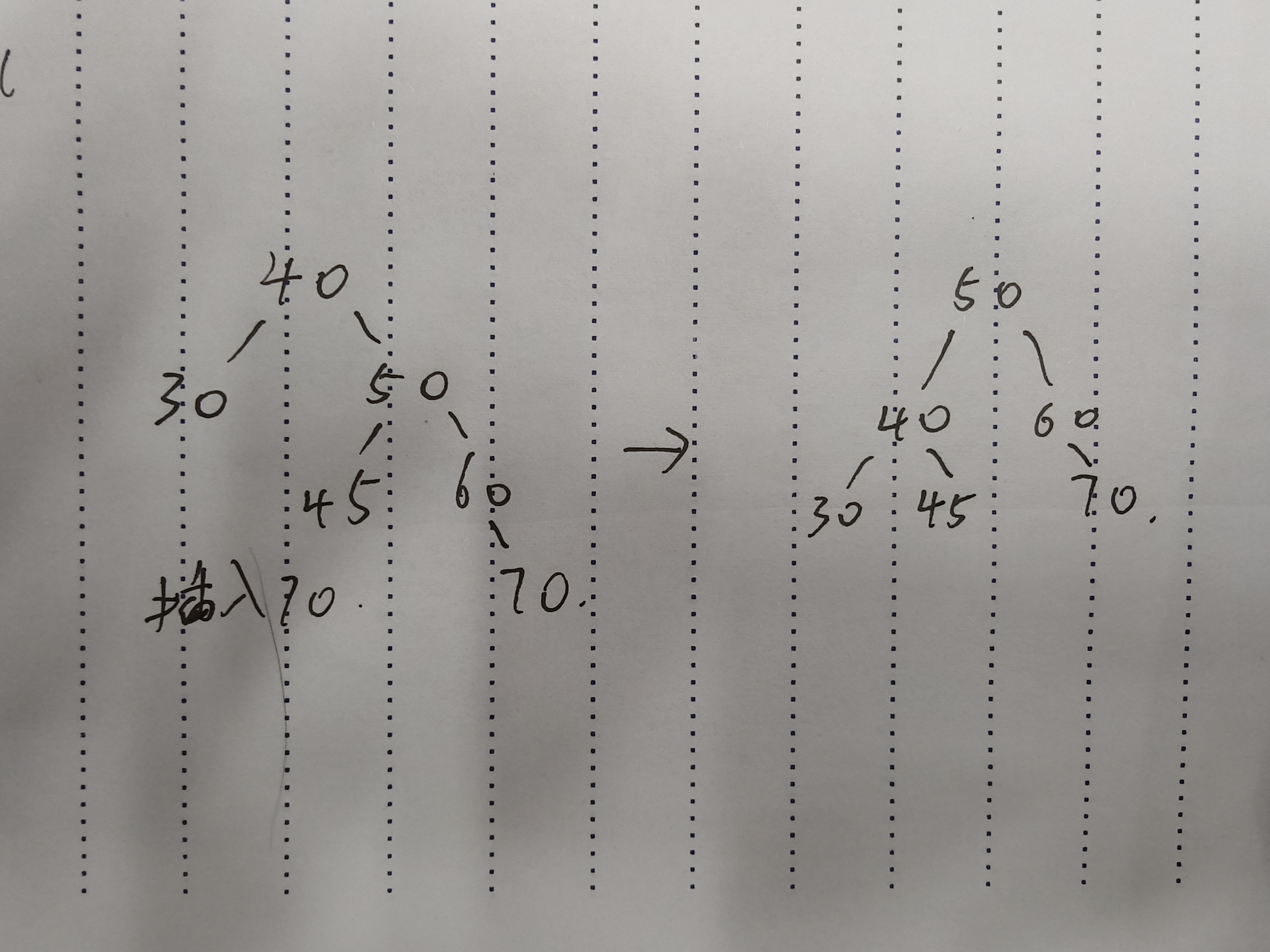
代码实现

private void rotateLeft(Node parent) {//记录节点Node subR = parent.right;Node subRL = subR.left;//旋转subR.left = parent;Node parentH = parent.parent;parent.parent = subR;parent.right = subRL;if (subRL != null) {//可能parent没有左节点subRL.parent = parent;}if (parent == root) {//那么curR就是新的根节点root = subR;subR.parent = null;} else {if (parentH.left == parent) {parentH.left = subR;//连接起新的根subR.parent = parentH;} else {parentH.right = subR;subR.parent = parentH;}}//旋转过后新的根的平衡因子肯定为0subR.bf = 0;parent.bf = 0;}

左右双旋  插入的位置是较高左子树的右边

 先对平衡因子为-2的50节点的左节点进行左单旋，需要将45的左节点拼到40的右节点，因为左旋使的45原来的左节点断开连接到40了，然后对50进行右单旋，最后就达到平衡了

代码实现

 private void rotateLeftRight(Node parent) {Node subL = parent.left;Node subLR = subL.right;int bf = subLR.bf;rotateLeft(subL);rotateRight(parent);//左右双旋后，左单旋或右单旋改变的bf已经不适用了//那么需要额外对插入在该节点的左右分俩种情况重新赋值if (bf == -1) {//插入的是在该节点的左边subL.bf = 0;subLR.bf = 0;parent.bf = 1;} else if(bf == 1){//bf == 1subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}

右左双旋 插入的位置时较高右子树的左边

 代码实现

    private void rotateRightLeft(Node parent) {Node subR = parent.right;Node subRL = subR.left;int bf = subRL.bf;rotateRight(subR);rotateLeft(parent);if (bf == 1) {//subRL == 1subR.bf = 0;subRL.bf = 0;parent.bf = -1;} else if(bf == -1){//bf == -1subR.bf = 1;subRL.bf = 0;parent.bf = 0;}}

那么可以发现，对于插入到二叉搜索树的数据能使树的高度差到2的情况，最基本就是这四种不考虑断指的，正好每种旋转方式能解决

而如果要考虑断支的情况那么还会多四种双旋断支和俩种单旋断支

而对于断支的拼接，右单旋是高层节点下降到右节点，他的左节点就释放了出来，而底层结点的右节点因为需要拼接到高层节所以被断开，而他断开的值，满足大于底层节点，而小于高层节点，那么正好可以拼接到高层节点的左节点去，很妙的

值的删除

使用替换删除法，对于到删除的节点使用他的左子树的最右节点来替换这个节点来达到删除的目的，因为左子树的最有节点满足小于左子树的所有节点，大于右子树的所有节点，那么使用他来进行替换删除是满足二叉搜索树的定义的没有问题的，当然使用右子树的最左节点也是可以成功的

代码实现

    public boolean del(int val) throws findError{//若不存在if (!contain(val)) {throw new findError("该值不存在 val = " + val);}//找到该节点Node cur = root;while (cur != null) {if (cur.val > val) {cur = cur.left;} else if (cur.val < val) {cur = cur.right;} else { // cur.val == valbreak;}}//替换删除法 用该节点的左支树的最右节点 cur一定存在Node tmp = cur.left;if (tmp == null) {//不存在左支树if (cur == root) {//为根root = root.right;} else {//不为根Node tmpH = cur.parent;//不知道parent是那个支树指向curif (tmpH.right == cur) {tmpH.right = cur.right;}else{tmpH.left = cur.right;}if (cur.right != null) {cur.right.parent = tmpH;}}return true;}//存在左支树的删除Node tmpR = tmp.right;//找到删除的最右左节点 while (tmpR != null && tmpR.right != null) {tmpR = tmpR.right;}//替换curif (tmpR != null) {cur.val = tmpR.val;tmpR.parent.right = null;//删除这个节点的连接} else {//tmpR == nullcur.val = tmp.val;cur.left = null;}return true;}public boolean contain(int val) {Node tmp = root;while (tmp != null) {if (val > tmp.val) {tmp = tmp.right;} else if (val < tmp.val) {tmp = tmp.left;} else {//相等说明存在return true;}}return false;}