当前位置： 首页 > news >正文

数据结构从入门到实战——二叉树

news 2025/10/21 10:13:57

目录

前言

一、二叉树链式结构的实现

1.1 二叉树的结构以及方法声明

1.2 手搓一个简单的二叉树（创建二叉树后面会详细讲解）

1.3 前序遍历

1.4 中序遍历

1.5 后续遍历

1.6 计算二叉树的节点个数

1.7 计算二叉树叶子节点的个数

1.8 计算二叉树的高度

1.9 二叉树的销毁

1.10 层序遍历（需要用到队列）

1.11 判断二叉树是否为完全二叉树

码云链接：https://gitee.com/a-qian-c-language/data-structure.git

前言

        在计算机科学的演进历程中，数据结构作为组织与管理信息的核心工具，始终扮演着至关重要的角色。面对日益复杂的数据处理需求，线性结构在表达层级关系与实现高效操作方面逐渐显现出局限性。为此，树形结构应运而生，以其天然的层次化特性，为解决分治、搜索、排序与表达式处理等复杂计算问题提供了强有力的模型支撑。

二叉树的基本功能：

  • 层次化组织结构：二叉树以唯一的根节点（Root）为逻辑起点，通过指针或引用建立明确的父子层级关系，自顶向下逐层扩展。每个节点最多拥有两个子节点——左子节点与右子节点，形成严格的二分分支结构。这种天然的分层特性使其能够高效地模拟现实世界中的层级关系（如组织架构、目录系统），并为分治算法（Divide and Conquer）提供理想的实现基础。
  • 高效的遍历机制：二叉树支持多种系统化的节点访问策略，主要包括前序遍历（根 → 左子树 → 右子树）、中序遍历（左子树 → 根 → 右子树）、后序遍历（左子树 → 右子树 → 根）和层序遍历（按深度逐层从左至右）。
  • 动态插入与删除：在二叉树的有序变体（如二叉搜索树，BST）中，元素的插入与删除操作可在维持结构有序性的前提下高效完成。通过比较节点值决定插入/删除路径，平均时间复杂度可达 O(log n)，显著优于线性结构的 O(n)。这一特性使其成为动态数据集合的理想选择，广泛应用于需要频繁增删查改的场景。
  • 天然支持递归操作：二叉树具有高度的自相似性——任一子树本身仍是一棵二叉树。这一特性使其与递归算法完美契合。无论是查找、插入、删除、遍历还是求树高、节点数等操作，均可通过简洁的递归函数实现，代码逻辑清晰，易于理解与维护，充分体现了“分而治之”的计算思想。
  • 多用途衍生结构：作为基础数据结构，二叉树是众多高级结构的构建基石。通过施加特定约束或优化策略，可衍生出平衡二叉搜索树（如AVL树、红黑树，保证 O(log n) 最坏性能）、堆（Heap，实现优先队列）、哈夫曼树（Huffman Tree，用于数据压缩）以及线段树、Trie树等。这些衍生结构在数据库索引、操作系统调度、文件压缩、字符串匹配等关键领域发挥着不可替代的作用。

        本文旨在系统阐述二叉树的基本功能与核心特性，深入剖析其在数据组织、遍历策略、动态操作及递归处理等方面的独特优势，并揭示其作为多种高级数据结构原型的重要地位。通过本篇内容，读者将能够全面理解二叉树的设计哲学与应用价值，为进一步探索算法与系统设计的深层原理奠定坚实基础。

正文开始：

一、二叉树链式结构的实现

项目结构如下：

1.1 二叉树的结构以及方法声明

BT.c

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>//二叉树的结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//前序遍历
void PrevOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后续遍历
void BackOrder(BTNode* root);//二叉树节点的个数
int TreeSize(BTNode* root);//叶子节点的个数
int TreeLeafSize(BTNode* root);//二叉树的高度
int TreeHeight(BTNode* root);//二叉树第K层的节点数
int TreeLevalSize(BTNode* root);//查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x);//二叉树的销毁
void BinaryTreeDestroy(BTNode* root);//二叉树的层序遍历
void TreeLevalOrder(BTNode* root);//判断一个二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root);

1.2 手搓一个简单的二叉树（创建二叉树后面会详细讲解）

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "BT.h"BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail!");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
//手搓一个二叉树
BTNode* CreateTree()
{//创建节点BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}int main()
{//手搓一个二叉树BTNode* root = CreateTree();return 0;
}

1.3 前序遍历

BT.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "BT.h"//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

测试结果如下：

1.4 中序遍历

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PrevOrder(root->left);printf("%d ", root->data);PrevOrder(root->right);
}

测试结果如下：

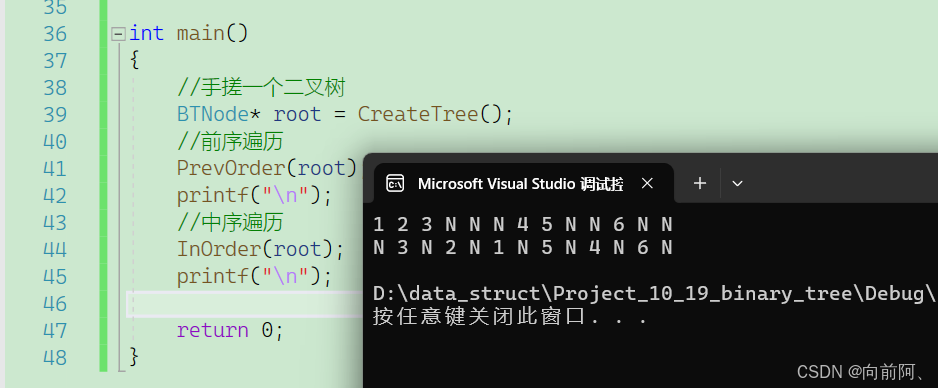
1.5 后续遍历

//后续遍历
void BackOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->data);}

测试结果如下：

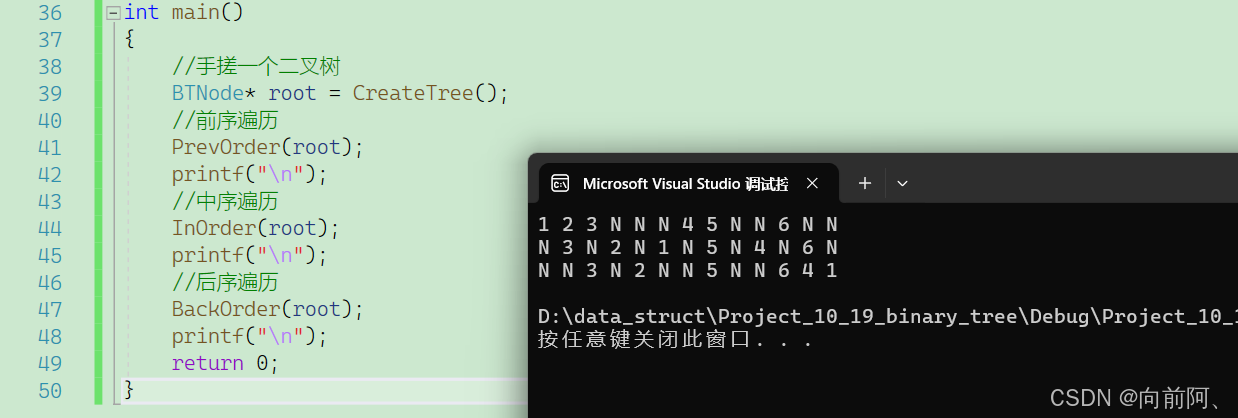
1.6 计算二叉树的节点个数

//二叉树节点的个数
int TreeSize(BTNode* root)
{if (root == NULL){return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}

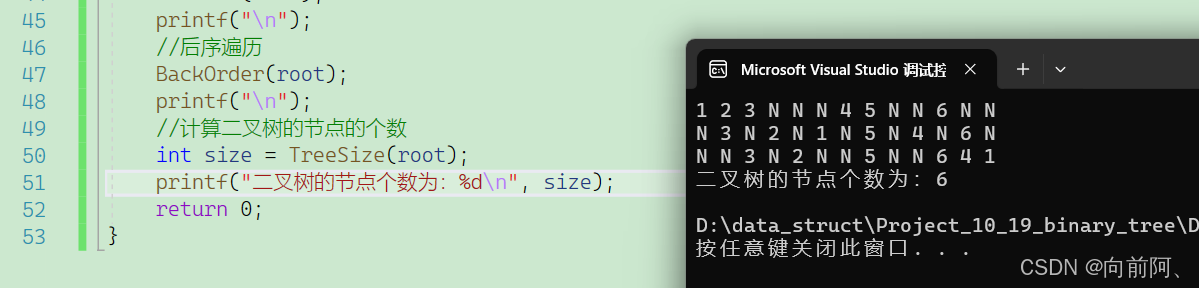
1.7 计算二叉树叶子节点的个数

//叶子节点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

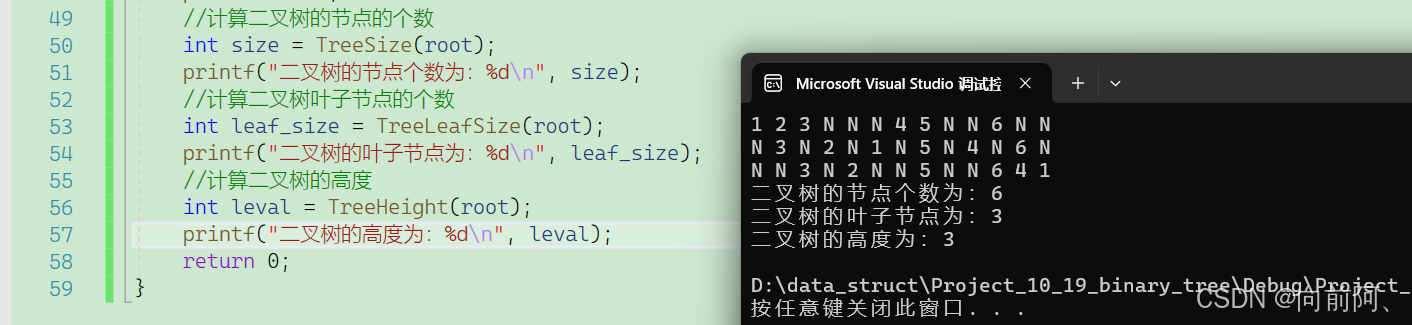
1.8 计算二叉树的高度

//二叉树的高度
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}

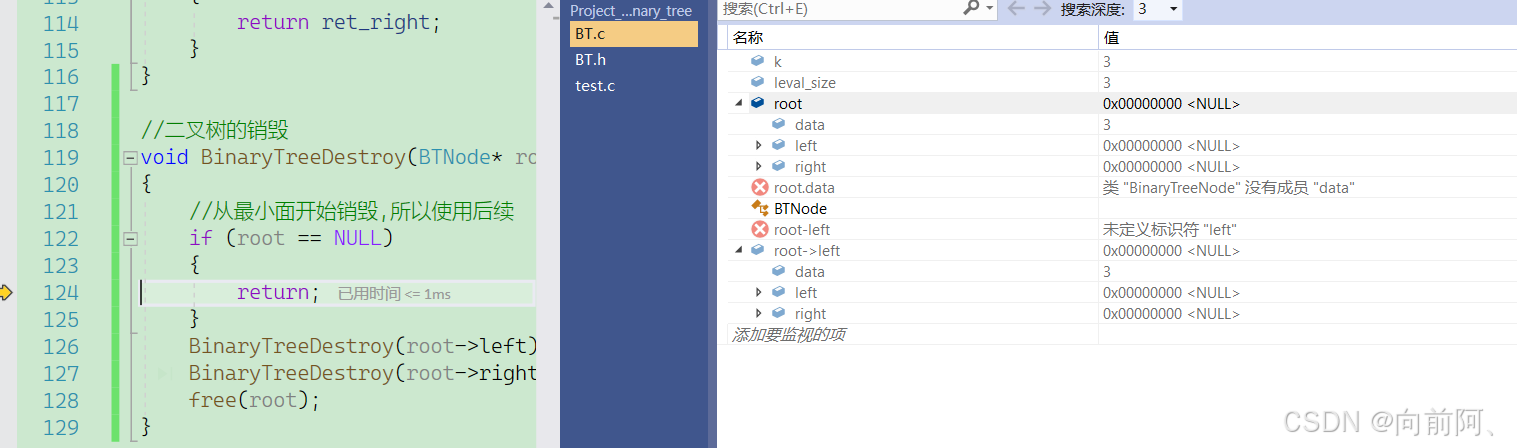
1.9 二叉树的销毁

//二叉树的销毁
void BinaryTreeDestroy(BTNode* root)
{//从最小面开始销毁,所以使用后续if (root == NULL){return;}BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);
}

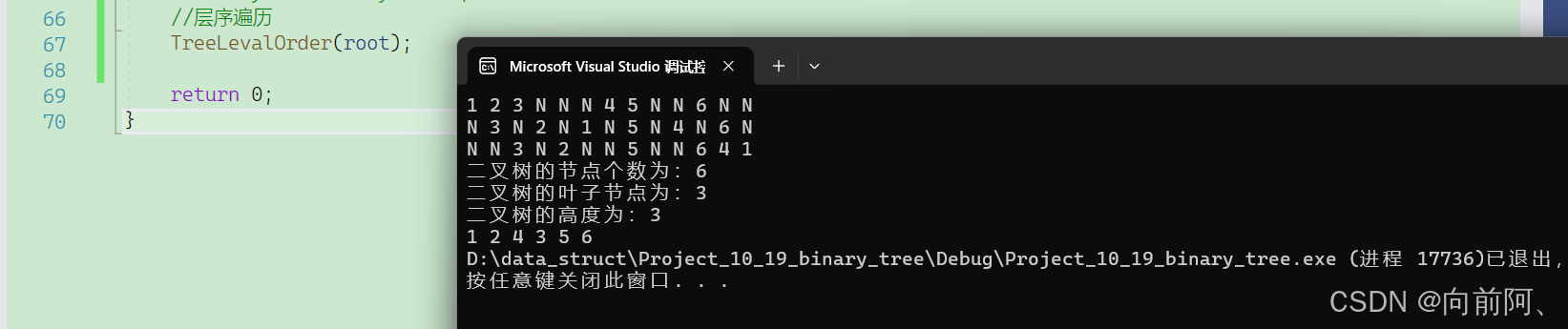
1.10 层序遍历（需要用到队列）

Q.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>//定义队列的结构
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Que;//初始化
void QueueInit(Que* pq);
//销毁
void QueueDestroy(Que* pq);//队尾插入
void QueuePush(Que* pq, QDataType x);
//对头删除
void QueuePop(Que* pq);//取队头的数据
QDataType QueueFront(Que* pq);
//取队尾的数据
QDataType QueueBack(Que* pq);//判断队列是否为空
bool QueueEmpty(Que* pq);
//取队列节点的个数
int QueueSize(Que* pq);

Q.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Q.h"//初始化
void QueueInit(Que* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}//销毁
void QueueDestroy(Que* pq)
{assert(pq);QNode* pcur = pq->phead;while (pcur){QNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}//队尾插入
void QueuePush(Que* pq, QDataType x)
{assert(pq);//创建节点QNode* node = (QNode*)malloc(sizeof(QNode));if (node == NULL){perror("malloc fail!");return;}node->val = x;//此时节点已经创建成功,开始往队列中插入if (pq->phead == NULL){pq->phead = pq->ptail = node;}else{pq->ptail->next = node;pq->ptail = node;}pq->size++;
}//对头删除
void QueuePop(Que* pq)
{assert(pq);assert(pq->size > 0);if (pq->phead == pq->ptail){free(pq->phead);pq->phead = NULL;pq->ptail = NULL;}else{QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}//取队头的数据
QDataType QueueFront(Que* pq)
{assert(pq);assert(pq->size > 0);return  pq->phead->val;
}//取队尾的数据
QDataType QueueBack(Que* pq)
{assert(pq);assert(pq->size > 0);return pq->ptail->val;
}//判断队列是否为空
bool QueueEmpty(Que* pq)
{return pq->size == 0;
}//取队列节点的个数
int QueueSize(Que* pq)
{return pq->size;
}
//二叉树的层序遍历
void TreeLevalOrder(BTNode* root)
{if (root == NULL){return;}//此时root肯定不是空，则将根节点插入队列中Que q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}
}

1.11 判断二叉树是否为完全二叉树

//判断一个二叉树是否为完全二叉树
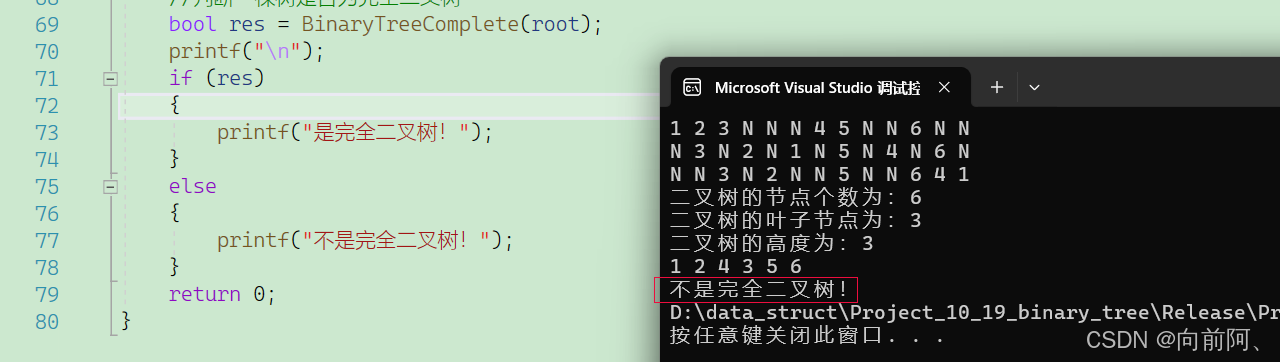
bool BinaryTreeComplete(BTNode* root)
{if (root == NULL){return false;}Que q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

http://www.dtcms.com/a/507919.html

相关文章：

  • 企业出海服务商合作全流程
  • Linux-绑定和解绑linux程序
  • 医疗器械注册三大路径对比
  • Python嵌套函数的参数传递详解
  • 下一代时序数据库标杆：解码Apache IoTDB“轻量级内核+AI原生架构“如何重构AIoT时代数据价值链​
  • 零食店网站构建策划报告大庆今天最新公告
  • 长宁怎么做网站优化好计算机女生就业方向
  • 负荷聚类及其在MATLAB中的实现
  • 环境搭建 | [入门级]VSCode（Cursor|Trae|Qoder）搭建Java(Springboot3)企业开发环境全流程
  • 怎么获取小红书用户笔记作品列表？item_search_shop_videoAPI接口指南
  • 盐城建站韩漫网站建设
  • 我的企业网站怎么seo网站 模板
  • 【Linux】深入理解进程（一）
  • 基于单片机的车辆超载报警系统设计及人数检测设计
  • 防止网站被克隆dedecms 网站地图插件
  • 做网站与网店运营263企业邮箱pop3设置
  • 解释 Python 的 GIL（全局解释器锁）机制及其对多线程的影响。
  • Conda_bashrc 初始化机制学习笔记
  • 用dw制作购物网站首页WordPress空间换到万网
  • Spring 4.0新特性全面解析
  • 世界之窗附近做网站公司门户网站的营销特点
  • neo4j密码忘记如何解决
  • React + TypeScript 企业级编码规范指南
  • React Router 路由模式详解：HashRouter vs BrowserRouter
  • 福田做网站怎么样下载网站模板
  • 每日一个C语言知识：C 结构体
  • 淘宝网中国站电脑版登录辽宁省建设工程招投标
  • sql数据库语法
  • 使用jmeter进行压力测试
  • 长期网站外包wordpress主题php详解