当前位置：首页 > news >正文

《小白学随机过程》第二章：随机过程——常见的随机过程(线性高斯过程和卡尔曼滤波)

news 2025/10/20 17:04:50

本文首先讲解了什么是高斯过程，这是一类随机过程的统称。在实际应用上，有多种随机过程都属于高斯过程，作为第二章的开篇，本章主要讲解了线性高斯过程，本章涉及以下要点：

按照时间是否连续、状态是否连续，对随机过程进行分类
对随机变量和随机过程标准化的数学定义
提供了一个高斯过程(通用)的仿真代码实现和示例图
阐述动态系统和随机过程的关系，以及什么是线性高斯动态系统
引出卡尔曼滤波，其状态方程描述的就是一个离散的线性高斯过程组成的动态序列
说明卡尔曼滤波状态公式 $u_t$ 的作用
提供了一个2D空间上的具体例子
提供了一个python仿真代码和示意图，说明线性高斯过程的建模过程(这也是进一步学习卡尔曼滤波的前提)

随机过程是描述随时间（或空间）演化的随机现象的数学模型。根据时间指标集 $T$ 和状态空间 $S$ 的性质，以及过程的统计特性，常见的随机过程可分为以下几类：

一、按时间与状态空间分类

类型	时间指标集 $T$	状态空间 $S$	典型例子
离散时间 + 离散状态	$\mathbb{N}$ 或 $\{0,1,2,\dots\}$	有限或可数集（如 $\mathbb{Z}$ ）	马尔可夫链、随机游走
离散时间 + 连续状态	$\mathbb{N}$	$\mathbb{R}^d$	ARMA 时间序列、GARCH 模型
连续时间 + 离散状态	$\infty)$	有限或可数集	泊松过程、生灭过程
连续时间 + 连续状态	$\infty)$	$\mathbb{R}^d$	布朗运动、Ornstein-Uhlenbeck 过程

二、经典随机过程详解

1. 高斯过程（Gaussian Process, GP）

1.1 定义

一个随机过程 $\{X(t)\}_{t \in T}$ 称为高斯过程，如果对任意有限个时间点 $t_1, \dots, t_n \in T$ ，随机向量 $(X(t_1), \dots, X(t_n))$ 服从多元正态分布。

✅ 高斯过程完全由其均值函数和协方差函数决定：

均值函数： $\mathbb{E}[X(t)]$
协方差函数（核函数）： $\text{Cov}(X(t), X(s))$

1.2 示例和图示、代码

下面我们将定义一个具体的高斯过程（Gaussian Process, GP），写出其均值函数和协方差函数（核函数），使用 Python（NumPy + Matplotlib）从该 GP 中采样 N 条轨迹并可视化。
我们选择一个经典且常用的高斯过程：

均值函数： $m (t) = 0$
协方差函数（RBF 核 / Squared Exponential Kernel）：
$\sigma^2 \exp\left( -\frac{(t - t')^2}{2\ell^2} \right)$
其中：
$\sigma^2 = 1.0$ ：信号方差（控制幅度）
$\ell = 0.5$ ：长度尺度（控制平滑性， $\ell$ 越小，函数越“抖”）

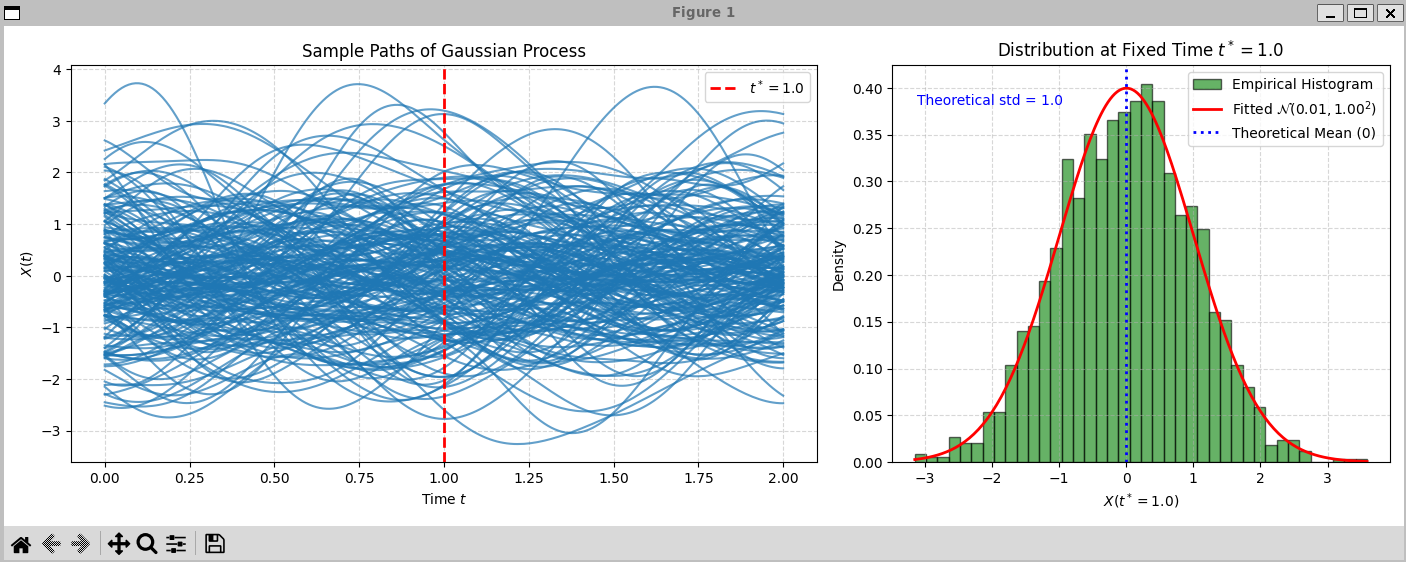
📌 这个 GP 生成的样本函数是无限可微、非常平滑的随机曲线。

Python 实现：采样 N 条轨迹。高斯过程在有限个点 $t_1, \dots, t_n$ 上的联合分布为：
$\mathbf{f} = [f(t_1), \dots, f(t_n)]^\top \sim \mathcal{N}(\mathbf{0}, \mathbf{K})$
其中 $\mathbf{K}_{ij} = k(t_i, t_j)$ 。我们通过 Cholesky 分解或特征值分解从该多元正态分布中采样。代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# ----------------------------
# 1. 设置高斯过程参数
# ----------------------------
T = np.linspace(0, 2, 200)          # 时间网格 [0, 2]，200 个点
t_star = 1.0                        # 固定时刻 t*
t_star_idx = np.argmin(np.abs(T - t_star))  # 找到最接近的索引n_trajectories = 200                 # 轨迹数量（用于可视化）
n_samples_hist = 2000               # 用于直方图的采样次数（越多越平滑）sigma = 1.0                         # 信号标准差
ell = 0.3                           # 长度尺度（控制平滑性）# ----------------------------
# 2. 构建协方差矩阵 (RBF 核)
# ----------------------------
T1, T2 = np.meshgrid(T, T)
K = sigma**2 * np.exp(-0.5 * (T1 - T2)**2 / ell**2)
K += 1e-8 * np.eye(len(T))         # 数值稳定性# Cholesky 分解
L = np.linalg.cholesky(K)# ----------------------------
# 3. 采样轨迹（用于绘图）
# ----------------------------
trajectories = []
for _ in range(n_trajectories):z = np.random.randn(len(T))f = L @ ztrajectories.append(f)# ----------------------------
# 4. 采样大量样本用于直方图（仅需 t_star 处的值）
# ----------------------------
samples_at_t_star = []
for _ in range(n_samples_hist):z = np.random.randn(len(T))f = L @ zsamples_at_t_star.append(f[t_star_idx])samples_at_t_star = np.array(samples_at_t_star)# ----------------------------
# 5. 绘图：轨迹 + 直方图
# ----------------------------
fig, axs = plt.subplots(1, 2, figsize=(14, 5), gridspec_kw={'width_ratios': [3, 2]})# --- 左图：随机过程轨迹 ---
for f in trajectories:axs[0].plot(T, f, color='C0', alpha=0.7)
axs[0].axvline(x=t_star, color='red', linestyle='--', linewidth=2, label=f'$t^* = {t_star}$')
axs[0].set_xlabel('Time $t$')
axs[0].set_ylabel('$X(t)$')
axs[0].set_title('Sample Paths of Gaussian Process')
axs[0].grid(True, linestyle='--', alpha=0.5)
axs[0].legend()# --- 右图：固定时刻 t* 的分布 ---
counts, bins, patches = axs[1].hist(samples_at_t_star, bins=40, density=True,alpha=0.6, color='green', edgecolor='black', label='Empirical Histogram'
)# 拟合正态分布
mu_emp = np.mean(samples_at_t_star)
sigma_emp = np.std(samples_at_t_star)
x = np.linspace(bins[0], bins[-1], 200)
pdf = norm.pdf(x, mu_emp, sigma_emp)
axs[1].plot(x, pdf, 'r-', linewidth=2, label=f'Fitted $\mathcal{{N}}({mu_emp:.2f}, {sigma_emp:.2f}^2)$')# 理论均值与方差（GP 在 t* 处的边际分布）
# 对于零均值 GP，X(t*) ~ N(0, k(t*, t*)) = N(0, sigma^2)
theoretical_std = sigma  # 因为 RBF 核在 t=t' 时为 sigma^2
axs[1].axvline(x=0, color='blue', linestyle=':', linewidth=2, label='Theoretical Mean (0)')
axs[1].text(0.05, 0.9, f'Theoretical std = {theoretical_std}', transform=axs[1].transAxes, color='blue')axs[1].set_xlabel(f'$X(t^*={t_star})$')
axs[1].set_ylabel('Density')
axs[1].set_title(f'Distribution at Fixed Time $t^* = {t_star}$')
axs[1].legend()
axs[1].grid(True, linestyle='--', alpha=0.5)plt.tight_layout()
plt.show()

执行效果如下所示(其中左边采样了200条轨迹进行显示，右图采样了2000条轨迹并固定时间统计直方图)：
在这里插入图片描述

2. 线性高斯过程（Liner Gaussian Process, LGP）

1.1 前置知识

建议首先了解控制理论中线性动态系统的状态空间表示方法，对理解线性高斯过程非常有帮助，参考：线性高斯系统的含义

1.2 定义

线性高斯过程（Linear Gaussian Process）是指一类由线性动态系统驱动、且所有噪声服从高斯分布的随机过程。它本质上是线性高斯状态空间模型（Linear Gaussian State-Space Model）中状态序列 ${x_t}$ 所构成的随机过程。其状态序列既是马尔可夫过程，又是高斯过程，广泛应用于滤波、控制、信号处理和经济建模等领域。

线性高斯过程是高斯过程，高斯过程不一定是线性高斯过程。

1.3 核心特征

线性：状态演化由线性方程描述；
高斯：初始状态和过程/观测噪声均为高斯分布；
马尔可夫性：当前状态仅依赖前一状态；
可解析推断：可用卡尔曼滤波（Kalman Filter）进行最优状态估计。

1.4 数学化表述

状态方程（系统动态）
$\mathbf{x}_t = \mathbf{F}_t \mathbf{x}_{t-1} + \mathbf{B}_t \mathbf{u}_t + \mathbf{w}_t, \quad \mathbf{w}_t \sim \mathcal{N}(0, \mathbf{Q}_t)$
观测方程（可选，用于滤波）
$\mathbf{z}_t = \mathbf{H}_t \mathbf{x}_t + \mathbf{v}_t, \quad \mathbf{v}_t \sim \mathcal{N}(0, \mathbf{R}_t)$
其中：
- $\mathbf{x}_t$ ：隐藏状态（如位置、速度、温度等）；
- $\mathbf{F}_t$ ：状态转移矩阵（线性动态）；
- $\mathbf{B}_t$ ：控制输入矩阵；
- $\mathbf{u}_t$ ：已知控制输入（如加速度指令、政策干预）；
- $\mathbf{w}_t, \mathbf{v}_t$ ：高斯过程噪声和观测噪声；
- $\mathbf{H}_t$ ：观测矩阵。

🔑 关键结论：由于线性变换 + 高斯噪声 ⇒ 高斯分布，因此任意有限个时刻的状态 $(\mathbf{x}_{t_1}, \ldots, \mathbf{x}_{t_n})$ 的联合分布是多元正态分布，故 $\{\mathbf{x}_t\}$ 是一个高斯过程（在离散时间、有限维意义上）。

1.5 例子

在雷达目标跟踪系统中，线性高斯随机过程被广泛用于建模目标的运动状态（如位置、速度）及其受噪声干扰的观测。下面以 2D 平面中 $N$ 个匀速运动目标 为例，给出完整的状态空间模型，并提供 Python 动态模拟代码。

状态空间模型(线性高斯过程)：我们采用恒定速度模型（Constant Velocity, CV）：
$\mathbf{x}_t = \begin{bmatrix} x_t \\ \dot{x}_t \\ y_t \\ \dot{y}_t \end{bmatrix} \quad \text{（位置 } x,y \text{ + 速度 } \dot{x}, \dot{y} \text{）}$
状态方程
$\mathbf{x}_t = \mathbf{F} \mathbf{x}_{t-1} + \mathbf{w}_t, \quad \mathbf{w}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{Q})$
其中状态转移矩阵（时间步长 $\Delta t$ ）：
$\mathbf{F} = \begin{bmatrix} 1 & \Delta t & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \Delta t \\ 0 & 0 & 0 & 1 \end{bmatrix}$
过程噪声协方差（假设加速度扰动是白噪声，且各向同性）：
$\mathbf{Q} = q \cdot \begin{bmatrix} \frac{\Delta t^4}{4} & \frac{\Delta t^3}{2} & 0 & 0 \\ \frac{\Delta t^3}{2} & \Delta t^2 & 0 & 0 \\ 0 & 0 & \frac{\Delta t^4}{4} & \frac{\Delta t^3}{2} \\ 0 & 0 & \frac{\Delta t^3}{2} & \Delta t^2 \end{bmatrix}$
其中 $q$ 是过程噪声强度。

$Q$ 模拟了模型未捕捉到的动态扰动，如：加速度突变，风力干扰，路面不平等原因
注意看：右边矩阵中出现了 $\Delta t^4$ $\Delta t^3$ $\Delta t^2$ 等结构，这些幂次不是随意设定的，来源于对加速度白噪声的积分，并结合了状态转移方程的线性结构。具体来说：

假设系统受到加速度为高斯白噪声的扰动；
通过连续时间随机微分方程（SDE）推导出离散化后的过程噪声协方差；
利用积分公式和期望运算，最终得到包含 $\Delta t^4$ $\Delta t^3$ $\Delta t^2$ 的 $Q$
详细推导涉及随机微分方程等知识，在此不再详细展开，读者根据需求可查阅相关资料。

观测方程
雷达通常测量位置（可能还有速度，但这里简化为仅位置）：
$\mathbf{z}_t = \mathbf{H} \mathbf{x}_t + \mathbf{v}_t, \quad \mathbf{v}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{R})$
观测矩阵：
$\mathbf{H} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}$
观测噪声协方差（例如）：
$\mathbf{R} = \begin{bmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2 \end{bmatrix}$

1.6 python代码

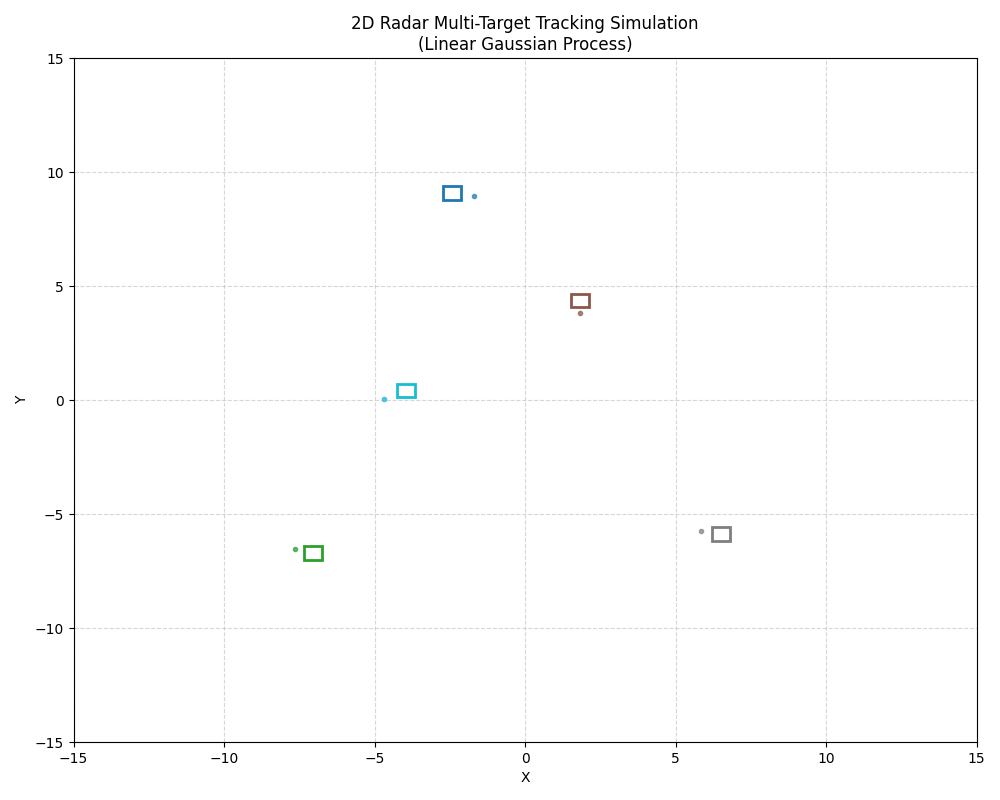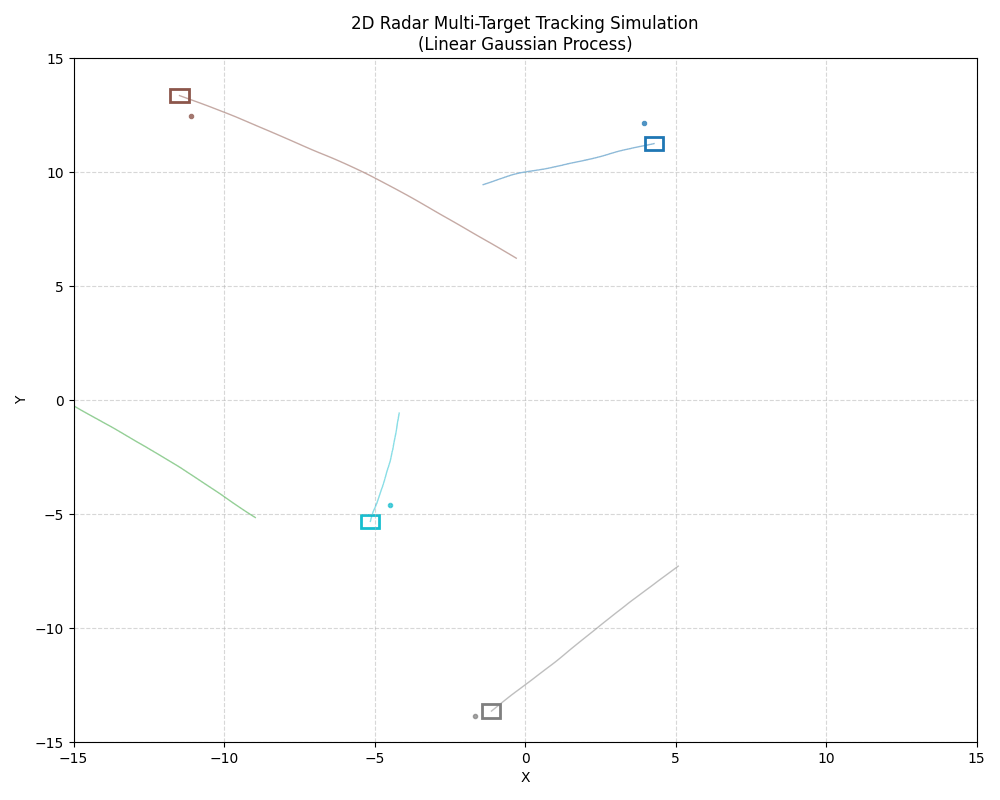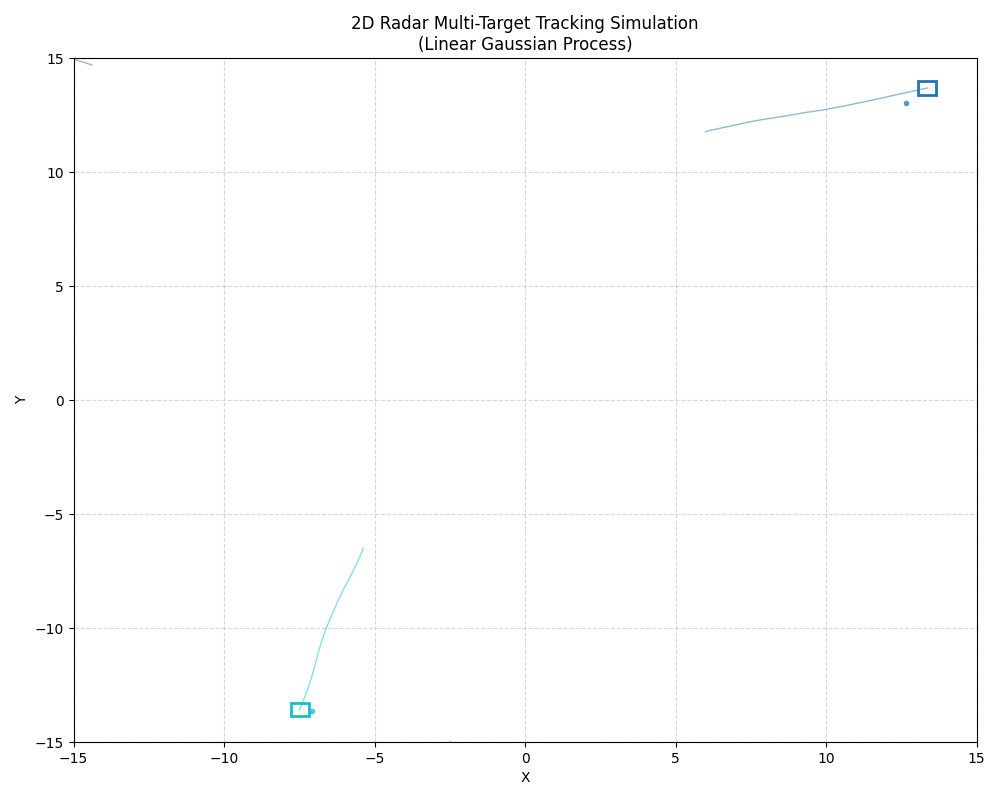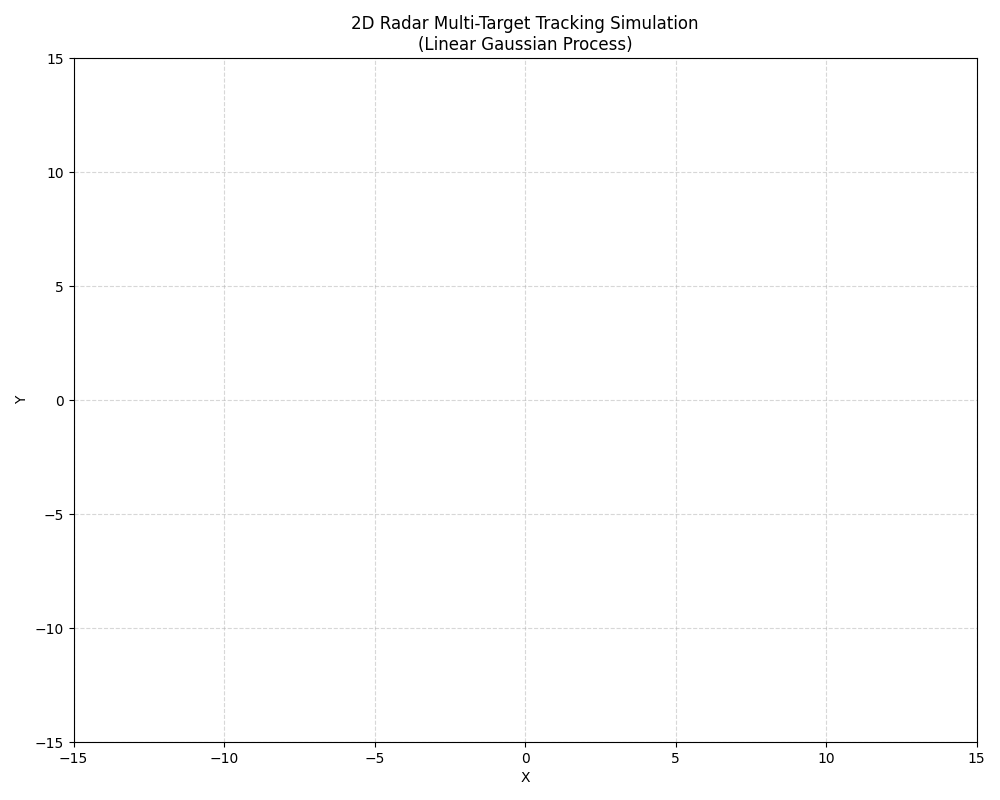
以下代码模拟 $N$ 个目标 在 $2 D$ 平面中匀速运动，受过程噪声扰动，并生成带观测噪声的雷达测量。使用 matplotlib.animation 实现动态可视化。（本模拟仅展示真实轨迹 + 带噪观测，不实现卡尔曼滤波（仅建模线性高斯过程本身））

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from matplotlib.animation import FuncAnimation# ----------------------------
# 参数设置
# ----------------------------
np.random.seed(42)  # 可复现N = 5                 # 目标数量
T = 200               # 时间步数
dt = 0.1              # 时间步长 (秒)# 过程噪声强度
q = 0.1
# 观测噪声标准差
sigma_x = 0.5
sigma_y = 0.5# 状态转移矩阵 F (4x4)
F = np.array([[1, dt, 0,  0],[0, 1,  0,  0],[0, 0,  1, dt],[0, 0,  0,  1]
])# 过程噪声协方差 Q (4x4)
Q_base = np.array([[dt**4/4, dt**3/2],[dt**3/2, dt**2   ]
])
Q = q * np.block([[Q_base, np.zeros((2,2))],[np.zeros((2,2)), Q_base]
])# 观测矩阵 H (2x4)
H = np.array([[1, 0, 0, 0],[0, 0, 1, 0]
])# 观测噪声协方差 R (2x2)
R = np.diag([sigma_x**2, sigma_y**2])# ----------------------------
# 初始化 N 个目标
# ----------------------------
# 每个目标状态: [x, vx, y, vy]
states = []
# 随机初始化位置（在 [-10, 10] 范围内）和速度（在 [-2, 2] 范围内）
for _ in range(N):x0 = np.random.uniform(-10, 10)y0 = np.random.uniform(-10, 10)vx0 = np.random.uniform(-2, 2)vy0 = np.random.uniform(-2, 2)states.append(np.array([x0, vx0, y0, vy0]))# 存储历史轨迹（用于绘制）
history = [[] for _ in range(N)]  # history[i] = [(x0,y0), (x1,y1), ...]
observations = [[] for _ in range(N)]  # 带噪观测# ----------------------------
# 模拟运动
# ----------------------------
for t in range(T):for i in range(N):# 添加过程噪声w = np.random.multivariate_normal(mean=np.zeros(4), cov=Q)states[i] = F @ states[i] + w# 记录真实位置x_true, y_true = states[i][0], states[i][2]history[i].append((x_true, y_true))# 生成带噪观测v = np.random.multivariate_normal(mean=np.zeros(2), cov=R)z = H @ states[i] + vobservations[i].append((z[0], z[1]))# 转换为 numpy 数组便于绘图
history = [np.array(traj) for traj in history]
observations = [np.array(obs) for obs in observations]# ----------------------------
# 动态可视化
# ----------------------------
fig, ax = plt.subplots(figsize=(10, 8))
ax.set_xlim(-15, 15)
ax.set_ylim(-15, 15)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title('2D Radar Multi-Target Tracking Simulation\n(Linear Gaussian Process)')
ax.grid(True, linestyle='--', alpha=0.5)# 为每个目标创建图形元素
rects = []
trails = []
obs_points = []colors = plt.cm.tab10(np.linspace(0, 1, N))for i in range(N):# 小矩形框表示目标（宽高 0.6）rect = patches.Rectangle((0, 0), 0.6, 0.6, linewidth=2, edgecolor=colors[i], facecolor='none')ax.add_patch(rect)rects.append(rect)# 轨迹线（真实路径）trail, = ax.plot([], [], color=colors[i], alpha=0.5, linewidth=1)trails.append(trail)# 观测点（雷达测量）obs_pt, = ax.plot([], [], 'o', color=colors[i], markersize=3, alpha=0.7)obs_points.append(obs_pt)# 初始帧
def init():for rect in rects:rect.set_xy((0, 0))for trail in trails:trail.set_data([], [])for obs in obs_points:obs.set_data([], [])return rects + trails + obs_points# 更新帧
def update(frame):for i in range(N):if frame < len(history[i]):x, y = history[i][frame]# 更新矩形位置（居中）rects[i].set_xy((x - 0.3, y - 0.3))# 更新轨迹（显示最近50步）start = max(0, frame - 50)trail_x = history[i][start:frame+1, 0]trail_y = history[i][start:frame+1, 1]trails[i].set_data(trail_x, trail_y)# 更新观测点if frame < len(observations[i]):ox, oy = observations[i][frame]obs_points[i].set_data([ox], [oy])return rects + trails + obs_points# 创建动画
ani = FuncAnimation(fig, update, frames=T,init_func=init, blit=True, interval=50
)plt.tight_layout()
plt.show()# 可选：保存为 GIF（需安装 pillow）
# ani.save('radar_tracking.gif', writer='pillow', fps=20)