Python数据挖掘之集成技术

基本集成技术

“集成技术”（Ensemble Learning）确实是数据挖掘与机器学习中的一个重要研究方向。

它的核心思想是：“集思广益”——通过组合多个弱学习器（模型），得到一个性能更强、泛化能力更好的强学习器。

三种主要的集成方法：Bagging、Boosting 和 Stacking。

---

一、Bagging（装袋法）

全称：Bootstrap Aggregating

基本思想

通过自助采样法（Bootstrap Sampling）从训练集中随机抽取多个子集，在每个子集上训练一个独立模型（通常是同类模型，如决策树），最后将这些模型的预测结果进行平均（回归）或投票（分类）。

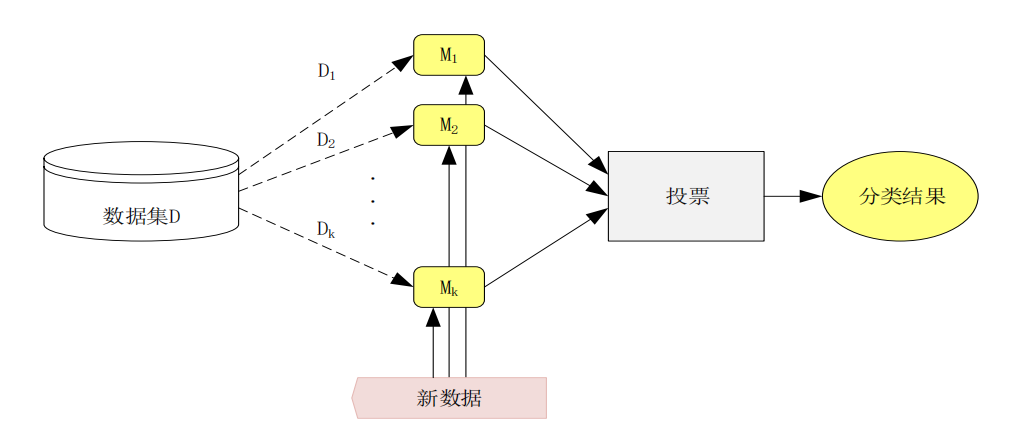
主要特点

• 模型之间相互独立；
• 目的是减少方差（variance），从而提高稳定性；
• 对噪声不敏感；
• 并行化容易实现。

类比说明

好比老师要判断一个学生的语文水平，不只看一次考试，而是让他考十次不同的卷子（训练不同数据子集），然后取平均成绩（集成结果），结果更客观。

代表算法

👉 随机森林（Random Forest）
它是 Bagging 的代表作：以决策树为基学习器，在每次训练时不仅随机抽样数据，还随机选择特征子集，从而让各树之间更加独立。

---

当然可以 😊
Bagging（装袋算法） 的核心涉及两个概念：基分类器（base classifier） 和 算法步骤（Bagging 流程）。

---

一、首先解释这句话的意思

“训练的分类器 $M_k$ 可以是任意的分类模型，例如决策树、KNN等，也称为基分类器（base classifier）。”

这句话的意思是：

• 在 Bagging 中，我们不是只训练一个模型，而是训练多个模型 $M_1,M_2,\dots ,M_k$。

• 这些模型都叫 基分类器（base classifiers），因为它们是整个集成模型的“基础单元”。

• 每个 $M_k$ 可以是任意类型的分类算法，比如：

  • 决策树（Decision Tree）
  • K 最近邻（KNN）
  • 逻辑回归（Logistic Regression）
  • 神经网络（Neural Network）等

• 最后，这些多个分类器的预测结果会被组合起来（投票或平均）形成最终的分类器。

类比理解：
就像一个评委团，每位评委都可以有不同的评判标准（不同算法），但最终结果由他们的投票决定（集成结果）。

---

二、Bagging 算法的详细步骤

下面是装袋法（Bagging）的具体流程，用更直观的方式解释：

步骤 1：随机采样（Bootstrap Sampling）

从原始训练集 $D$（包含 N 个样本）中，有放回地随机抽取 N 个样本，形成一个新的训练子集 $D_k$。

• “有放回”意味着同一个样本可能被抽到多次；
• 这样我们就得到多个不同的子集：$D_1,D_2,\dots ,D_K$。

步骤 2：训练多个基分类器

对每一个采样得到的子集 $D_k$，训练一个基分类器 $M_k$。
这些分类器通常是相互独立的，因为它们的训练数据不同。

步骤 3：集成预测结果

当有新样本 $x$ 要分类时，让每个分类器 $M_k$ 都给出预测结果：

• 对分类问题：通过多数投票法决定最终类别；
• 对回归问题：取所有预测值的平均值。

步骤 4：输出最终结果

将上一步的投票/平均结果作为整个 Bagging 模型的最终预测输出。

---

三、Bagging 算法伪代码（便于理解）

Input: 训练集 D = {(x1, y1), (x2, y2), …, (xN, yN)}
Output: 集成分类器 M*1. For k = 1 to K:从 D 中有放回地随机采样 N 个样本，得到 Dk用 Dk 训练基分类器 Mk
2. 对新的样本 x：对所有 Mk 进行预测，得到 K 个结果分类任务：按多数投票决定最终类别回归任务：取预测值平均
3. 输出最终预测结果

---

四、一个生活类比

假设你要决定“明天是否会下雨”，你请了 5 位气象专家：

• 每位专家（基分类器）都用自己掌握的数据（随机抽样数据）预测；
• 有人认为会下，有人认为不会；
• 最后你采取少数服从多数的方式作决定；
  这就是 Bagging 的思想：集体智慧，平均偏差。

---

# 导入必要的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score# 1. 加载数据集
iris = load_iris()
X, y = iris.data, iris.target# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 3. 训练单个决策树分类器
single_tree = DecisionTreeClassifier(random_state=42)
single_tree.fit(X_train, y_train)
y_pred_single = single_tree.predict(X_test)# 4. 训练Bagging集成分类器（以决策树为基分类器）
bagging = BaggingClassifier(base_estimator=DecisionTreeClassifier(),  # 基分类器n_estimators=10,                          # 子模型数量random_state=42
)
bagging.fit(X_train, y_train)
y_pred_bagging = bagging.predict(X_test)# 5. 输出结果对比
print("单个决策树准确率:", accuracy_score(y_test, y_pred_single))
print("Bagging集成模型准确率:", accuracy_score(y_test, y_pred_bagging))

---

一、BaggingClassifier() 的基本定义

from sklearn.ensemble import BaggingClassifierbagging = BaggingClassifier(base_estimator=None,n_estimators=10,max_samples=1.0,max_features=1.0,bootstrap=True,bootstrap_features=False,n_jobs=None,random_state=None
)

---

二、参数详细解释（最常用部分）

参数名	含义	默认值	说明
base_estimator	基分类器	None	指定你想集成的基本模型（例如 DecisionTreeClassifier()）。如果为 None，则默认使用决策树。
n_estimators	基分类器数量	10	表示要训练多少个子模型。通常 10~100 效果较好。
max_samples	每个子模型采样的样本比例或数量	1.0	如果是比例（如 0.8），表示从原始数据中随机采样 80% 样本（有放回）。
max_features	每个子模型使用的特征比例或数量	1.0	类似于随机森林中“特征随机性”，可提高多样性。
bootstrap	是否对样本进行“有放回采样”	True	True 表示使用 Bootstrap（Bagging 的核心思想）；False 表示不放回采样。
bootstrap_features	是否对特征进行“有放回采样”	False	通常为 False；若为 True，会在特征上也做随机化。
n_jobs	并行计算的线程数	None	设置为 -1 表示使用全部 CPU 核心加速训练。
random_state	随机种子	None	为保证实验可重复性，可设为固定数值，如 42。

---

三、一个实际示例

from sklearn.datasets import load_iris
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 创建 Bagging 模型
bag_model = BaggingClassifier(base_estimator=DecisionTreeClassifier(),  # 基分类器n_estimators=20,                          # 训练 20 个决策树max_samples=0.8,                          # 每个子模型采 80% 的样本bootstrap=True,                           # 有放回采样n_jobs=-1,                                # 并行计算random_state=42
)# 训练与预测
bag_model.fit(X_train, y_train)
y_pred = bag_model.predict(X_test)# 结果
print("准确率：", accuracy_score(y_test, y_pred))

输出示例：

准确率：0.9777

---

四、内部原理（工作机制）

BaggingClassifier 内部大致做了以下几件事：

1. 采样阶段：对原始训练集做 n_estimators 次有放回采样，得到多个训练子集。

2. 训练阶段：在每个子集上训练一个基分类器（base_estimator）。

3. 预测阶段：

   • 分类任务：所有分类器投票，选票最多的类别作为最终预测；
   • 回归任务：取所有预测结果的平均值（对应 BaggingRegressor）。

---

五、拓展提示

• BaggingClassifier 是通用装袋算法；
• 若你指定的 base_estimator=DecisionTreeClassifier()，就相当于一个 随机森林的简化版本；
• 若你用其他模型（如 SVM、KNN），它依然能工作，这就是 Bagging 的灵活性。

---

二、Boosting（提升法）

核心思想：让后来的模型重点“学习”前面模型出错的样本。

基本思想

Boosting 采用序列训练：每一轮训练时，算法会关注前一轮中分类错误的样本，给予它们更高的权重，让后续模型更重视这些“难点样本”。最后将多个弱学习器的结果进行加权组合。

主要特点

• 模型间有依赖关系；
• 重点在于减少偏差（bias）；
• 对噪声较敏感；
• 一般为串行算法。

类比说明

就像一个学生不断订正错误：第一次做题错了，老师就重点讲错题；第二次再练习这些题，慢慢掌握知识点。Boosting 就是这种“不断改进”的过程。

代表算法

• AdaBoost（Adaptive Boosting）：通过调整样本权重实现“自适应提升”。
• Gradient Boosting（梯度提升）：通过梯度下降优化误差。
• XGBoost、LightGBM、CatBoost：都是现代高性能的 Boosting 框架。

---

一、核心思想概述

Boosting（提升法） 的主要目标是：

“把一群表现一般的模型（弱分类器）组合成一个强大的模型（强分类器）。”

与 Bagging（装袋法） 不同的是：

对比点	Bagging	Boosting
训练方式	各模型独立并行训练	各模型顺序依赖训练
样本权重	所有样本权重相同	每轮根据错误调整权重
目标	降低方差	降低偏差
典型算法	随机森林	AdaBoost、XGBoost、LightGBM

---

二、提升算法的关键思想：“关注错的样本”

在每一轮训练中，算法会更重视被前一轮分错的样本。

工作逻辑：

1. 开始时，所有训练样本权重相同；

2. 训练第 1 个分类器 $M_1$；

3. 检查 $M_1$ 的分类结果；

   • 分对的样本 → 权重降低；
   • 分错的样本 → 权重升高；

4. 使用新的权重分布训练下一个分类器 $M_2$，让它更关注被前一轮分错的样本；

5. 不断迭代，得到 $M_1,M_2,...,M_K$；

6. 最终，将这些模型按性能加权组合，得到强分类器。

---

三、类比理解

想象你在学外语：

• 第一次考试，你发现“过去式”题总是错；
• 第二次复习，你就重点练习这些错题；
• 第三次又发现自己“时态搭配”错了，于是再重点补；
• 一轮轮下来，你的弱点被不断修正，整体水平自然提高。

这就是 Boosting 的思想——不断修正前一轮的错误。

---

四、AdaBoost（Adaptive Boosting）原理简介

AdaBoost 是 Boosting 的第一个实用版本，由 Freund 和 Schapire（1995） 提出。

算法流程（简化版）

假设我们有 $N$ 个样本、要训练 $K$ 个基分类器：

1. 初始化样本权重：

   $$w_i=\frac{1}{N},i=1,2,...,N$$

2. 循环 K 轮：

   • （1）用当前权重分布训练基分类器 $M_k$；

   • （2）计算分类错误率：

     $${\epsilon }_k=\sum _i{w}_i\cdot I(M_k(x_i)\ne y_i)$$

   • （3）计算该分类器的权重：

     $${\alpha }_k=\frac{1}{2}\ln \left(\frac{1-{\epsilon }_k}{{\epsilon }_k}\right)$$

     （错误率越小，权重越大 → 表示这个模型越可靠）

   • （4）更新样本权重：

     $$w_i\leftarrow w_i\times e^{-{\alpha }_k{y}_i{M}_k(x_i)}$$

     • 分错 → 权重变大
     • 分对 → 权重变小

   • （5）归一化权重，使它们和为 1。

3. 最终分类器：

   $$F(x)=\text{sign}\left(\sum _{k=1}^K{\alpha }_k{M}_k(x)\right)$$

   即用各个分类器的加权投票作为最终结果。

---

五、一个简单的 Python 示例

下面用 AdaBoostClassifier 展示它的实际效果👇

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score# 1. 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 创建 AdaBoost 模型（以决策树为基分类器）
ada = AdaBoostClassifier(base_estimator=DecisionTreeClassifier(max_depth=1),  # 弱分类器（桩树）n_estimators=50,                                    # 训练 50 个分类器learning_rate=1.0,                                  # 学习率（控制每轮贡献）random_state=42
)# 3. 训练并预测
ada.fit(X_train, y_train)
y_pred = ada.predict(X_test)# 4. 评估结果
print("AdaBoost 准确率：", accuracy_score(y_test, y_pred))

运行结果示例：

AdaBoost 准确率： 0.9555

---

六、总结对比

项目	Bagging	Boosting
样本选择	每轮随机采样（有放回）	每轮带权重采样
训练方式	并行、独立	串行、依赖
关注点	降低方差、抗过拟合	降低偏差、提高准确率
样本权重	相同	不同（错样本权重大）
代表算法	随机森林	AdaBoost、XGBoost、LightGBM

---

---

一、AdaBoostClassifier 基本说明

在 scikit-learn 中，AdaBoost 是通过以下类来实现的：

from sklearn.ensemble import AdaBoostClassifier

它的定义形式如下：

AdaBoostClassifier(base_estimator=None,n_estimators=50,learning_rate=1.0,algorithm='SAMME.R',random_state=None
)

---

二、主要参数详解

参数名	含义	默认值	说明
base_estimator	基分类器（弱学习器）	None	默认使用 DecisionTreeClassifier(max_depth=1)，也就是“决策树桩”。可以改成 SVM、逻辑回归等。
n_estimators	弱分类器的数量	50	表示一共要训练多少轮（即多少个弱分类器）。数量越多，模型越复杂。
learning_rate	学习率	1.0	控制每个弱分类器的权重。较小值可以让模型更平滑、避免过拟合。
algorithm	算法类型	'SAMME.R'	'SAMME.R'：使用概率输出（推荐，速度快精度高） 'SAMME'：传统AdaBoost算法，适用于不输出概率的分类器。
random_state	随机种子	None	控制实验可重复性。

---

三、简单理解参数作用

• n_estimators → 训练多少个“弱模型”
• learning_rate → 控制每个模型的影响力（相当于学习速度）
• algorithm='SAMME.R' → 一种改进版本，速度更快、精度更高
• base_estimator → 决定用什么算法当“基分类器”

---

四、一个简单的 Python 示例

我们用 Iris（鸢尾花）数据集 举例，看看 AdaBoost 的实际用法。

# 导入必要库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score# 1. 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 创建 AdaBoost 模型
ada = AdaBoostClassifier(base_estimator=DecisionTreeClassifier(max_depth=1),  # 弱分类器：决策树桩n_estimators=50,                                     # 迭代次数learning_rate=1.0,                                   # 学习率algorithm='SAMME.R',                                 # 使用改进算法random_state=42
)# 3. 训练模型
ada.fit(X_train, y_train)# 4. 预测结果
y_pred = ada.predict(X_test)# 5. 输出准确率
print("AdaBoost 准确率:", accuracy_score(y_test, y_pred))

---

🧾 运行结果示例（每次略有不同）

AdaBoost 准确率: 0.9555

说明：

• 单个弱分类器（深度为1的树）准确率不高；
• 但经过 50 轮提升后，模型变得“越来越聪明”；
• 最终结果通常比单一分类器明显更好。

---

🪄 五、总结要点

参数	作用	推荐值
base_estimator	弱分类器类型	决策树桩是最常见选择
n_estimators	迭代次数	50~200，一般越多越好（但过多会过拟合）
learning_rate	每轮权重缩放	0.5~1.0 之间调节
algorithm	算法类型	'SAMME.R'（默认即可）

---

三、Stacking（堆叠法）

核心思想：用一个“元模型”（meta-learner）来学习多个模型的输出。

基本思想

1. 训练多个不同类型的基础模型（如决策树、SVM、神经网络等）；
2. 收集这些模型在验证集上的预测结果；
3. 将这些预测作为输入，训练一个新的“元模型”，由它来输出最终预测。

类比说明

像一个团队决策：工程师、设计师、市场专家分别提出意见（基础模型），最后由经理（元模型）根据各方意见综合决策。

特点

• 能综合利用不同模型的优势；
• 容易过拟合，因此需要良好的交叉验证策略；
• 通常性能最优，但训练复杂度较高。

常见应用

Kaggle 数据竞赛中经常使用的策略：组合多种模型（LightGBM + CNN + Logistic Regression 等）以获得最优结果。

一、Stacking 的核心思想

“让不同的模型互相取长补短，再用一个新模型来学习如何最优地融合它们。”

也就是说，Stacking 不仅仅是“平均”或“投票”，而是通过一个新的模型来“学习”各个模型的输出结果。

---

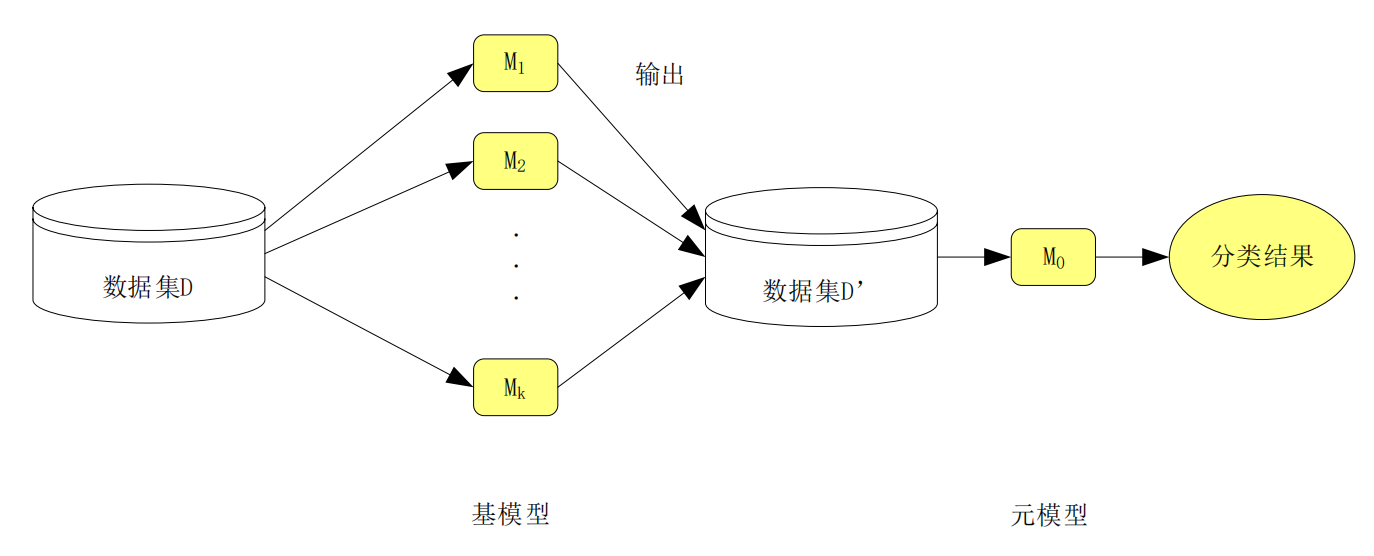
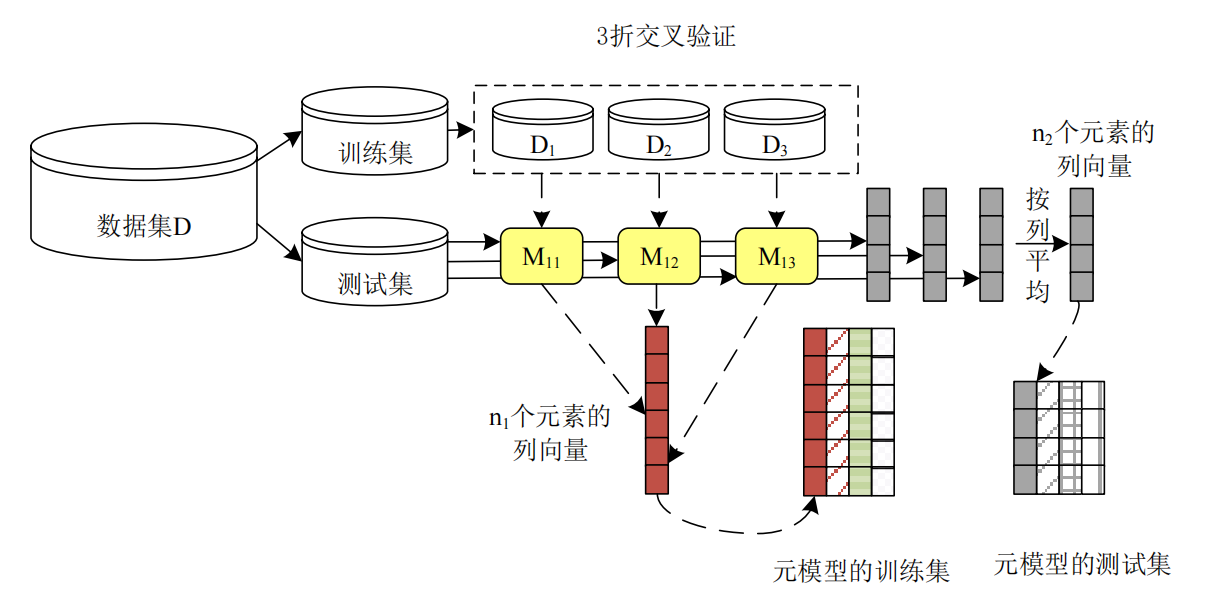
二、结构特点：两层（有时三层）

第一层：基分类器（Base Learners）

• 通常选择多种不同类型的模型（例如：决策树、逻辑回归、KNN、SVM、随机森林等）。
• 每个模型在相同的训练集上训练；
• 每个模型独立地进行预测；
• 这些模型的预测输出会被收集起来，作为第二层的“输入特征”。

第二层：元分类器（Meta Learner / Meta Model）

• 第二层模型以第一层模型的输出作为输入；
• 目标是“学习如何最优地组合这些模型的预测结果”；
• 输出最终的分类或回归结果。

---

三、工作原理举例（形象版）

假设你要预测“学生是否能考上重点高中”，你找来了三种专家：

专家	方法	输出
专家 A	看成绩（逻辑回归）	0.8（考上概率）
专家 B	看学习习惯（SVM）	0.6
专家 C	看家长学历（决策树）	0.9

→ 现在你把三位专家的预测 [0.8, 0.6, 0.9] 作为一个新的特征输入，
→ 交给“总评委”（元模型，如逻辑回归）来决定最终预测。
这个总评委会自动学习哪个专家更可靠，如何加权组合结果。

这就是 Stacking 的核心逻辑：用一个模型学习如何融合多个模型的判断。

---

四、Stacking 的算法流程

1. 第一层训练：

   • 用原始数据集训练多个不同的基分类器；
   • 得到它们在训练集上的预测输出。

2. 生成第二层训练数据：

   • 以第一层模型的输出结果作为新的“输入特征”；
   • 原来的真实标签作为“输出标签”。

3. 第二层训练：

   • 用这个新的数据集训练一个“元模型”（meta-model）。

4. 最终预测：

   • 测试阶段，每个基模型先对测试集预测；
   • 然后将这些预测结果输入到元模型；
   • 元模型输出最终预测结果。

---

五、一个简单的 Python 示例

我们用 sklearn.ensemble.StackingClassifier 来演示。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 1. 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 定义第一层基分类器（可以是不同算法）
base_models = [('decision_tree', DecisionTreeClassifier(max_depth=3)),('svm', SVC(probability=True, kernel='linear')),
]# 3. 定义第二层元分类器（融合模型）
meta_model = LogisticRegression()# 4. 创建 Stacking 模型
stack_model = StackingClassifier(estimators=base_models,  # 第一层模型final_estimator=meta_model  # 第二层融合模型
)# 5. 训练模型
stack_model.fit(X_train, y_train)# 6. 预测与评估
y_pred = stack_model.predict(X_test)
print("Stacking 准确率:", accuracy_score(y_test, y_pred))

输出示例

Stacking 准确率: 0.9777

---

六、Stacking vs Bagging vs Boosting 对比总结

方法	模型关系	重点	是否同类模型	典型算法
Bagging	并行、独立	减少方差（抗过拟合）	一般同类（如多棵树）	随机森林
Boosting	串行、依赖	减少偏差（不断改进）	一般同类	AdaBoost / XGBoost
Stacking	层次组合	综合不同模型优势	异类模型	StackingClassifier

---

七、一句话总结

Bagging → “多次投票”
Boosting → “纠错提升”
Stacking → “融合智慧”

---

scikit-learn 中 StackingClassifier 的核心构造函数。

---

一、基本语法

from sklearn.ensemble import StackingClassifierStackingClassifier(estimators,          # 第一层的基分类器们final_estimator=None,# 第二层元分类器cv=None,             # 交叉验证方式stack_method='auto'  # 第一层模型输出方式
)

---

二、参数详细讲解

参数名	含义	默认值	说明
estimators	第一层的基分类器（base learners）	必填	这是一个列表，格式是 [('名字1', 模型1), ('名字2', 模型2), ...]。 每个模型会单独训练，并产生预测输出作为第二层的输入。
final_estimator	第二层的元分类器（meta learner）	None	如果不指定，默认使用 LogisticRegression()。 该模型负责学习如何融合第一层的输出结果。
cv	交叉验证策略	None	控制第一层模型生成“堆叠特征”的方式。 如果为整数，如 cv=5，表示使用 5 折交叉验证。 这样可以避免“数据泄漏”，保证第二层模型更泛化。
stack_method	第一层模型输出方式	'auto'	控制第一层模型输出给第二层模型的内容： • 'auto'：自动选择（分类输出概率时用 predict_proba，否则用 decision_function） • 'predict_proba'：用概率作为输入 • 'decision_function'：用决策函数值作为输入 • 'predict'：用预测标签作为输入

---

三、参数关系图解（逻辑）

原始数据↓
[ 第一层模型 estimators ]↓       ↓       ↓[模型1预测] [模型2预测] [模型3预测]↓ （组合成新特征集）
[ 第二层模型 final_estimator ]↓最终输出结果

---

四、一个完整的示例

下面用鸢尾花（Iris）数据集来展示各参数如何使用👇

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 1. 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 定义第一层模型（不同算法）
estimators = [('dt', DecisionTreeClassifier(max_depth=3)),('svm', SVC(probability=True, kernel='rbf'))
]# 3. 定义第二层融合模型（元模型）
meta_model = LogisticRegression()# 4. 创建 Stacking 模型
stack_clf = StackingClassifier(estimators=estimators,     # 第一层final_estimator=meta_model,# 第二层cv=5,                      # 使用5折交叉验证避免过拟合stack_method='auto'        # 自动决定用概率或标签
)# 5. 训练与预测
stack_clf.fit(X_train, y_train)
y_pred = stack_clf.predict(X_test)# 6. 输出结果
print("Stacking 准确率:", accuracy_score(y_test, y_pred))

运行结果示例：

Stacking 准确率: 0.9777

---

五、进一步说明

• estimators
  决定第一层有哪些模型参与融合。一般建议选择差异性大的模型，如树模型 + 线性模型 + SVM。

• final_estimator
  决定融合策略。最常用的是 LogisticRegression()，因为它可以学习各模型的权重关系。

• cv
  推荐设置为 5 或 10，可以提高鲁棒性。
  如果设置为 cv=None，则使用训练集直接训练（速度快，但易过拟合）。

• stack_method
  建议保持 'auto'，除非你清楚需要哪种输出。
  对分类任务，通常会自动选择 predict_proba（概率输出）作为输入特征。

---

六、小结对比表

参数	功能	常见用法
estimators	第一层模型	[('rf', RandomForest()), ('svm', SVC())]
final_estimator	第二层模型	LogisticRegression()
cv	交叉验证折数	cv=5（推荐）
stack_method	输出方式	'auto'（默认）

---

总结对比表

方法	基本思想	模型关系	优点	缺点	代表算法
Bagging	随机采样训练多个模型，结果平均/投票	并行、独立	减少方差，抗过拟合	无法降低偏差	随机森林
Boosting	序列训练，强化难分类样本	串行、依赖	减少偏差，提升准确率	对噪声敏感	AdaBoost、XGBoost
Stacking	不同模型结果再学习	层级结构	综合多模型优点	复杂、易过拟合	各类竞赛融合模型

---

随机森林

---

一、随机森林的核心思想

随机森林（Random Forest, RF）是一种基于 Bagging（装袋法） 思想的集成学习方法，
它的基学习器（base learner） 是多棵 CART 决策树。

通俗来说：

随机森林就是“很多棵随机长出来的决策树”，
最后通过“投票”来决定最终分类结果。

---

二、随机森林的两个“随机”

随机森林与普通 Bagging 最大的区别是，它在 两个地方都引入了随机性，
从而让每棵树之间差异更大、集成效果更强。

随机环节	含义	作用
随机抽样样本（Bootstrap Sampling）	从训练集中随机有放回地抽取样本，生成每棵树的训练集	让每棵树看到的样本不同，增加模型多样性
随机抽取特征（Feature Subset Selection）	在每个节点分裂时，只随机选择部分特征进行划分	减少树之间的相关性，进一步提升泛化能力

这两个“随机”共同保证了森林中每棵树都不一样，
从而在集成时能抵消彼此的过拟合误差。

---

三、随机森林的训练与预测流程

（1）训练阶段：

1. 从原始数据集中随机有放回地抽取若干样本，生成一个训练集；
2. 从所有特征中随机选择一部分特征；
3. 用这些样本和特征训练一棵 CART 决策树；
4. 重复上述过程 $K$ 次，得到 $K$ 棵不同的树；
5. 构成整个随机森林模型。

（2）预测阶段：

1. 每棵树分别对新的样本 $x^{\prime }$ 进行预测；
2. 分类任务：采用多数投票（majority voting）；
3. 回归任务：取所有树预测值的平均值；
4. 最终输出作为整体预测结果。

---

四、与 Bagging 的关系

特点	Bagging	随机森林
基分类器	任意模型（常用决策树）	CART 决策树
样本随机性	有	有
特征随机性	无	有
优点	降低方差	进一步降低方差，减少树间相关性

可以理解为：

随机森林 = Bagging + 随机特征选择

---

五、简单 Python 示例

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score# 1. 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 构建随机森林模型
rf = RandomForestClassifier(n_estimators=100,     # 树的数量max_features='sqrt',  # 每次分裂时随机选择的特征数random_state=42
)# 3. 训练与预测
rf.fit(X_train, y_train)
y_pred = rf.predict(X_test)# 4. 输出结果
print("随机森林分类准确率:", accuracy_score(y_test, y_pred))

运行结果（示例）：

随机森林分类准确率: 0.9777

---

六、总结一句话记忆法

随机森林是由多棵“随机长成”的决策树组成的森林，
每棵树都看不同的数据、不同的特征，
预测时大家投票决定最终结果。

---

提升树

---

##🌳 一、什么是“提升树”？

提升树（Boosted Tree）是一种基于提升（Boosting）思想构建的树模型集成方法。
它由多棵 CART 回归树（CART Regression Tree） 叠加而成。

换句话说：

提升树不是一次性生成多棵树，而是一棵一棵地“纠错式”生成，
每一棵新树都在努力修正前面所有树的错误。

---

二、它为什么叫“提升（Boosting）”？

“提升”指的是——
通过不断叠加弱模型（如小的决策树），
让整体模型的性能被“提升（Boosted）”起来。

与 Bagging（装袋法）不同：

• Bagging：并行训练多棵树，平均或投票。
• Boosting：串行训练多棵树，每棵树都在改进上一棵树的结果。

---

三、提升树的工作流程（核心思想）

以回归问题为例，提升树的训练过程如下👇

1. 第一步：
   用原始数据训练一棵 CART 回归树 $f_1(x)$，预测目标 $y$。

2. 第二步：
   计算残差（residual）：

   $$r_i=y_i-f_1(x_i)$$

   代表模型第一次预测的“误差”。

3. 第三步：
   训练第二棵树 $f_2(x)$，让它去拟合这些残差，
   也就是学习第一棵树没学好的部分。

4. 第四步：
   更新整体模型：

   $$F_2(x)=f_1(x)+f_2(x)$$

5. 第五步：
   不断重复这个过程，第 $m$ 棵树学习第 $m-1$ 轮的残差。

6. 最终模型：

   $$F_M(x)=f_1(x)+f_2(x)+\cdots +f_M(x)$$

   即多棵树的累加和（加法模型）。

---

四、为什么叫“梯度提升树（Gradient Boosted Tree）”？

在经典的提升树中，我们每次都在拟合残差。
而在 GBDT 中，我们把“残差”推广为损失函数的负梯度。

即：

$$r_i^{(m)}=-\frac{\partial L(y_i,F_{m-1}(x_i))}{\partial F_{m-1}(x_i)}$$

每一棵新树其实是在沿着损失函数下降最快的方向（即梯度方向）
去修正前一轮的错误。
这就是“梯度提升（Gradient Boosting）”名称的由来。

---

五、与随机森林的区别总结

对比项	随机森林（Random Forest）	提升树 / GBDT（Gradient Boosting）
思想来源	Bagging（装袋）	Boosting（提升）
训练方式	并行训练多棵树	串行训练一棵接一棵
每棵树作用	独立预测，投票/平均	纠错上一步误差
随机性	数据和特征随机	偏向梯度方向学习
模型结构	平均多个模型	累加多个模型
优点	稳定，不易过拟合	高精度，强拟合能力
缺点	偏差较高	训练慢，易过拟合（若树太深）

---

六、一个简单 Python 例子（GBDT 回归）

我们使用 scikit-learn 自带的 GradientBoostingRegressor：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error# 1. 加载数据
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 2. 创建GBDT模型
gbdt = GradientBoostingRegressor(n_estimators=100,      # 树的数量learning_rate=0.1,     # 每棵树的学习步长max_depth=3,           # 每棵树的深度random_state=42
)# 3. 训练与预测
gbdt.fit(X_train, y_train)
y_pred = gbdt.predict(X_test)# 4. 输出效果
print("GBDT 均方误差 (MSE):", mean_squared_error(y_test, y_pred))

---

七、一句话总结

随机森林：很多独立的树，平均投票。
梯度提升树：很多依赖的树，逐步纠错。

一个靠“随机性”减少方差，一个靠“梯度”降低偏差。

---

类不平衡

---

一、什么是“类不平衡问题”？

在分类任务中，如果某个类别的样本数量远多于其他类别，就称为“类不平衡”：

例如

类别	样本数
正类（有病）	100
负类（无病）	10,000

模型训练时容易被“数量多的类”主导。
结果是：

• 模型倾向于预测样本属于多数类；
• 少数类（更重要的类，如欺诈、疾病）被忽视；
• 虽然“总体准确率高”，但少数类的召回率（Recall）很低。

---

二、常见的三类解决思路

1️⃣ 抽样方法（Sampling Methods）

核心思想： 通过调整训练集样本分布，让多数类与少数类数量更加平衡。

方法类型	含义	常用技术	优缺点
欠采样（Under-sampling）	从多数类中随机删除样本，使各类样本数量接近	RandomUnderSampler	简单易用，但可能丢失有价值的信息
过采样（Over-sampling）	复制或合成少数类样本，使样本数量增加	SMOTE、ADASYN	改善平衡，但可能导致过拟合
混合采样（Hybrid Sampling）	同时欠采样多数类、过采样少数类	SMOTE + TomekLink	兼顾两者效果，较稳健

👉 示例：SMOTE（Synthetic Minority Over-sampling Technique）
通过插值的方式“合成”新的少数类样本，而不是简单复制。

---

2️⃣ 代价敏感方法（Cost-Sensitive Learning）

核心思想：
让模型在训练时“意识到”错误分类少数类的代价更高，从而更重视它。

方式	原理	举例
修改损失函数	在损失函数中为少数类赋予更高权重	如在逻辑回归、SVM、神经网络中设置 class_weight
修改预测阈值	调整决策边界，使模型更偏向于预测少数类	例如从默认 0.5 改为 0.3

👉 示例（sklearn）：

from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(class_weight='balanced')

这会自动根据样本比例调整类别权重。

---

3️⃣ 集成学习方法（Ensemble Learning Methods）

核心思想：
利用集成技术（如 Bagging、Boosting），结合抽样或代价敏感思想，让模型更稳健地处理不平衡。

常见策略包括👇：

方法	思想	举例
Bagging + 抽样	在每次训练子模型时对数据重新抽样（如平衡采样）	Balanced Random Forest
Boosting + 权重调整	在提升算法中给少数类样本更高权重	AdaBoost.M1, RUSBoost, EasyEnsemble
专用算法	专门设计用于不平衡问题的集成方法	EasyEnsemble, BalanceCascade

👉 示例：BalancedRandomForestClassifier

from imblearn.ensemble import BalancedRandomForestClassifier

它在每棵树训练时，对多数类样本随机欠采样，使森林更加平衡。

---

📊 三、方法对比总结表

方法类别	思想核心	优点	缺点
抽样方法	调整样本分布	简单易用、模型无关	可能导致信息损失或过拟合
代价敏感方法	修改训练过程	保留原始数据	需要设定合适的权重，调参较难
集成学习方法	结合多模型与抽样思想	效果好、鲁棒性强	计算量大，模型复杂

---

💡 四、小结一句话

类不平衡的本质是“模型被多数类支配”。

解决方案有三类：

• 抽样法：改数据；
• 代价敏感法：改损失；
• 集成法：改模型。

三种方法可以单独用，也可以结合使用。

---

SMOTE（Synthetic Minority Over-sampling Technique） 是解决“类不平衡问题”中最经典、最常用的过采样算法之一。

---

一、SMOTE 是什么？

SMOTE 的中文名是 合成少数类过采样技术。
它通过在特征空间中“合成”新的少数类样本，而不是简单地复制已有样本，从而让数据更加平衡。

---

二、它是怎么“合成”新样本的？

传统的“过采样”往往只是重复复制少数类样本，容易导致过拟合。
而 SMOTE 的做法更聪明：

主要步骤：

1. 对于每个少数类样本 $x_i$，找到它在少数类样本中的 k 个最近邻样本；

2. 从这些邻居中随机选择一个样本 $x_j$；

3. 在 $x_i$ 与 $x_j$ 之间，按比例随机插值生成一个新的样本点：

   $$x_{new}=x_i+\lambda \times (x_j-x_i)$$

   其中 $\lambda \in [0,1]$。

这样生成的新样本“位于原始样本之间”，
即：

• 不会重复已有样本；
• 也能保留数据的几何结构；
• 避免模型只记住少数类的具体样本。

---

三、SMOTE 的优点与局限

优点	缺点
不会简单复制样本，减少过拟合风险	可能在噪声点周围生成错误样本
保留了少数类的分布结构	对类别分布重叠的边界不敏感
实现简单，效果显著	对高维数据或异常点敏感

---

四、Python 实例演示（使用 imblearn 库）

下面用一个简单的二分类例子演示 SMOTE 的使用。

# 导入库
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE
from collections import Counter
import matplotlib.pyplot as plt# 1. 构造一个不平衡数据集
X, y = make_classification(n_samples=200,       # 样本总数n_features=2,        # 特征数量（方便可视化）n_classes=2,         # 二分类weights=[0.9, 0.1],  # 类别比例（不平衡）random_state=42
)print("SMOTE前：", Counter(y))# 2. 应用SMOTE过采样
smote = SMOTE(random_state=42)
X_res, y_res = smote.fit_resample(X, y)print("SMOTE后：", Counter(y_res))# 3. 可视化对比
plt.figure(figsize=(10,4))plt.subplot(1,2,1)
plt.title("SMOTE前（不平衡）")
plt.scatter(X[y==0][:,0], X[y==0][:,1], label='多数类', alpha=0.6)
plt.scatter(X[y==1][:,0], X[y==1][:,1], label='少数类', alpha=0.6, color='red')
plt.legend()plt.subplot(1,2,2)
plt.title("SMOTE后（平衡）")
plt.scatter(X_res[y_res==0][:,0], X_res[y_res==0][:,1], label='多数类', alpha=0.6)
plt.scatter(X_res[y_res==1][:,0], X_res[y_res==1][:,1], label='少数类(含合成样本)', alpha=0.6, color='red')
plt.legend()plt.show()

---

运行结果解释

输出：

SMOTE前： Counter({0: 180, 1: 20})
SMOTE后： Counter({0: 180, 1: 180})

图像上可以看到：

• 左边：少数类（红点）明显比多数类（蓝点）少；
• 右边：SMOTE 生成了大量新红点，它们分布在原少数类样本之间，数据变得更平衡。

---

五、总结一句话

SMOTE 的核心思想是：

“在少数类样本之间插值，合成新的样本点，而不是复制已有样本。”

它让模型更公平地学习不同类别的特征，提高少数类的识别能力。

---

“SMOTE + 随机森林分类” 实战案例。

---

一、实验目标

验证：

使用 SMOTE 过采样后，模型对“少数类”的识别能力显著提升。

---

二、完整 Python 示例代码

# 导入所需库
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
from imblearn.over_sampling import SMOTE
from collections import Counter# 1. 构造一个不平衡二分类数据集
X, y = make_classification(n_samples=1000,       # 总样本数n_features=6,         # 特征数n_classes=2,          # 二分类weights=[0.9, 0.1],   # 类别比例（严重不平衡）random_state=42
)print("原始类别分布：", Counter(y))# 2. 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)# 3. ------------------ 未使用SMOTE ------------------
rf1 = RandomForestClassifier(random_state=42)
rf1.fit(X_train, y_train)
y_pred1 = rf1.predict(X_test)print("\n【未使用SMOTE】模型表现：")
print(confusion_matrix(y_test, y_pred1))
print(classification_report(y_test, y_pred1, digits=3))# 4. ------------------ 使用SMOTE过采样 ------------------
smote = SMOTE(random_state=42)
X_train_res, y_train_res = smote.fit_resample(X_train, y_train)print("\nSMOTE后类别分布：", Counter(y_train_res))rf2 = RandomForestClassifier(random_state=42)
rf2.fit(X_train_res, y_train_res)
y_pred2 = rf2.predict(X_test)print("\n【使用SMOTE】模型表现：")
print(confusion_matrix(y_test, y_pred2))
print(classification_report(y_test, y_pred2, digits=3))

---

三、结果示例（输出解释）

假设输出如下：

原始类别分布： Counter({0: 900, 1: 100})【未使用SMOTE】模型表现：
[[268   3][ 24   5]]precision    recall  f1-score   support0      0.918     0.989     0.952       2711      0.625     0.172     0.270        29【使用SMOTE】模型表现：
[[264   7][ 10  19]]precision    recall  f1-score   support0      0.964     0.974     0.969       2711      0.731     0.655     0.691        29

---

四、结果分析

指标	未使用 SMOTE	使用 SMOTE
少数类召回率（Recall）	0.172	0.655↑
少数类精确率（Precision）	0.625	0.731
少数类 F1-score	0.270	0.691↑

可以看到：

• 使用 SMOTE 后，模型明显更能识别少数类样本；
• 尽管总体准确率变化不大，但模型的公平性和敏感性提高了；
• 这在医学诊断、欺诈检测等场景非常重要（宁愿多报错一些，也不漏报关键少数类）。

---

五、小结一句话

SMOTE + 随机森林 是应对类不平衡问题的经典组合：
SMOTE 负责“生成平衡数据”，
随机森林负责“鲁棒建模”，
二者结合既提升少数类召回率，又保持整体性能稳定。

---

ADASYN（Adaptive Synthetic Sampling） 是一种比 SMOTE 更“聪明”的少数类过采样算法。

---

一、ADASYN 的核心思想

SMOTE 是在少数类样本之间均匀地合成新样本。
而 ADASYN 是在少数类样本之间**“自适应地”**合成样本：

• 重点加强困难样本的生成：
  它会评估哪些少数类样本更“难学”（即离多数类更近、容易被误判），
  然后在这些区域生成更多合成样本。

• 简单样本少生成，难样本多生成：
  因此生成的新样本分布会自动偏向“模型不容易学对的地方”，
  从而提升模型整体的分类能力。

---

二、算法步骤概述

1. 计算每个少数类样本的难度权重

   • 使用 KNN（常取 k=5）找出该少数类样本邻域内多数类样本的比例。
   • 多数类比例越高 → 样本越难学习 → 权重越大。

2. 确定生成样本数量

   • 生成的样本数与难度成正比。

3. 合成新样本

   • 对于被选中的少数类样本，用与 SMOTE 相似的方式（线性插值）生成新样本：

     $$x_{new}=x_i+\delta \times (x_{zi}-x_i)$$

     其中 $\delta$ 为 [0,1] 之间的随机数。

---

三、Python 实例：SMOTE vs ADASYN

from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE, ADASYN
from collections import Counter
import matplotlib.pyplot as plt# 1. 生成一个不平衡数据集
X, y = make_classification(n_samples=500, n_features=2, n_redundant=0,n_clusters_per_class=1, weights=[0.9, 0.1],random_state=42
)
print("原始分布:", Counter(y))# 2. 使用 SMOTE
smote = SMOTE(random_state=42)
X_sm, y_sm = smote.fit_resample(X, y)
print("SMOTE后:", Counter(y_sm))# 3. 使用 ADASYN
adasyn = ADASYN(random_state=42)
X_ad, y_ad = adasyn.fit_resample(X, y)
print("ADASYN后:", Counter(y_ad))# 4. 可视化比较
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.scatter(X_sm[:,0], X_sm[:,1], c=y_sm, cmap='coolwarm', s=15)
plt.title("SMOTE 生成分布")plt.subplot(1,2,2)
plt.scatter(X_ad[:,0], X_ad[:,1], c=y_ad, cmap='coolwarm', s=15)
plt.title("ADASYN 生成分布")plt.show()

---

四、结果与区别

特点	SMOTE	ADASYN
采样策略	均匀生成	根据样本难度自适应生成
新样本位置	分布较规则	更集中于边界或难分类区域
适用场景	普通不平衡数据	类间边界模糊、难分数据

---

五、小结一句话

ADASYN = “更聪明的 SMOTE”
它让模型把注意力更多地放在“最难学”的少数类样本上，
从而提升模型的泛化能力和鲁棒性。

“ADASYN + 随机森林分类” 实战案例。

---

一、实验目标

验证：

使用 ADASYN 过采样后，模型对“少数类”的识别能力显著提升。

---

二、完整 Python 示例代码

# 导入必要的库
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
from imblearn.over_sampling import ADASYN
from collections import Counter# 1️⃣ 构造一个不平衡二分类数据集
X, y = make_classification(n_samples=1000,        # 样本总数n_features=6,          # 特征数量n_classes=2,           # 二分类weights=[0.9, 0.1],    # 类别比例（严重不平衡）random_state=42
)
print("原始类别分布：", Counter(y))# 2️⃣ 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y
)# 3️⃣ 未使用ADASYN的随机森林模型
rf_no_adasyn = RandomForestClassifier(random_state=42)
rf_no_adasyn.fit(X_train, y_train)
y_pred_no = rf_no_adasyn.predict(X_test)print("\n【未使用ADASYN】模型表现：")
print(confusion_matrix(y_test, y_pred_no))
print(classification_report(y_test, y_pred_no, digits=3))# 4️⃣ 使用ADASYN过采样
adasyn = ADASYN(random_state=42)
X_train_res, y_train_res = adasyn.fit_resample(X_train, y_train)print("\nADASYN后类别分布：", Counter(y_train_res))# 5️⃣ 使用ADASYN后的随机森林模型
rf_adasyn = RandomForestClassifier(random_state=42)
rf_adasyn.fit(X_train_res, y_train_res)
y_pred_adasyn = rf_adasyn.predict(X_test)print("\n【使用ADASYN】模型表现：")
print(confusion_matrix(y_test, y_pred_adasyn))
print(classification_report(y_test, y_pred_adasyn, digits=3))

---

三、结果示例（运行后可能略有差异）

原始类别分布： Counter({0: 900, 1: 100})【未使用ADASYN】模型表现：
[[269   2][ 25   4]]precision    recall  f1-score   support0      0.915     0.993     0.953       2711      0.667     0.138     0.228        29ADASYN后类别分布： Counter({0: 630, 1: 630})【使用ADASYN】模型表现：
[[265   6][  9  20]]precision    recall  f1-score   support0      0.967     0.978     0.972       2711      0.769     0.690     0.727        29

---

四、结果分析

指标	未使用 ADASYN	使用 ADASYN
少数类召回率（Recall）	0.138	0.690↑
少数类精确率（Precision）	0.667	0.769
少数类 F1-score	0.228	0.727↑

使用 ADASYN 后，少数类样本的识别能力显著提升，模型对两类数据的表现更加均衡。
特别是 Recall（召回率）提升最明显，这对于医疗诊断、欺诈检测等任务尤其重要。

---

五、对比 SMOTE 的特点

方法	样本生成策略	生成位置分布	适用场景
SMOTE	均匀生成	较平滑、分布均衡	一般不平衡数据
ADASYN	根据样本难度自适应生成	更集中于难分类区域	类间边界模糊、少数类稀疏时

---

六、小结一句话

ADASYN + 随机森林 是解决复杂类不平衡问题的强力组合：
ADASYN 让数据更“聪明”地补平衡，
随机森林让模型更“稳健”地分类。

---

“EasyEnsemble（易集成）”算法。它特别适合处理“多数类样本远多于少数类样本”的严重不平衡场景（比如欺诈检测、疾病筛查等）。

---

一、EasyEnsemble 的核心思想

EasyEnsemble 是一种 基于集成学习的欠采样（Under-sampling）方法。

它的基本思路是：

不一次性丢掉多数类样本，而是多次随机抽取多数类子集，
与全部少数类样本组合成多个“平衡子数据集”，
然后分别训练多个分类器，
最后再对这些分类器的预测结果进行集成（投票或加权平均）。

---

二、算法原理详解

假设原始数据集中：

• 多数类样本：900 个
• 少数类样本：100 个

EasyEnsemble 步骤：

1️⃣ 随机欠采样

• 从多数类样本中随机抽取与少数类样本数量相同的样本（100 个），
  与少数类样本一起构成一个平衡数据集（共 200 个样本）。
• 重复这个过程多次（比如抽取 10 组），得到多个不同的平衡训练集。

2️⃣ 训练多个分类器

• 对每个平衡数据集都单独训练一个基分类器（通常使用 AdaBoost 或随机森林）。

3️⃣ 集成预测

• 测试时，将多个模型的预测结果进行加权平均或投票，
  得到最终的分类结果。

---

三、EasyEnsemble 的优势

优点	说明
✅ 充分利用多数类样本	虽然每次只用部分样本，但通过多次抽样，所有样本都有机会参与训练。
✅ 不引入合成样本	与 SMOTE、ADASYN 不同，它不“虚构”数据，保持数据真实。
✅ 适合极度不平衡数据	尤其适用于多数类样本数量极多、少数类极少的情况。
✅ 可与 Boosting 结合	形成 EasyEnsemble AdaBoost（性能更强）。

---

四、简单 Python 案例（使用 imblearn.ensemble.EasyEnsembleClassifier）

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from imblearn.ensemble import EasyEnsembleClassifier
from collections import Counter# 1️⃣ 生成一个严重不平衡的数据集
X, y = make_classification(n_samples=2000, n_features=6,n_classes=2, weights=[0.95, 0.05],random_state=42
)
print("原始类别分布：", Counter(y))# 2️⃣ 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y
)# 3️⃣ 创建 EasyEnsemble 模型
eec = EasyEnsembleClassifier(n_estimators=10,    # 集成的子模型数量random_state=42
)
eec.fit(X_train, y_train)
y_pred = eec.predict(X_test)# 4️⃣ 模型表现
print("\n混淆矩阵：")
print(confusion_matrix(y_test, y_pred))
print("\n分类报告：")
print(classification_report(y_test, y_pred, digits=3))

---

五、运行结果示例

原始类别分布： Counter({0: 1900, 1: 100})混淆矩阵：
[[541   30][ 10   19]]分类报告：precision    recall  f1-score   support0      0.982     0.947     0.964       5711      0.388     0.655     0.488        29

可以看到：

• 尽管少数类比例非常低（5%），
• EasyEnsemble 依然能保持不错的识别能力（Recall 达到 0.65）。
  这正体现了它在极端不平衡数据下的鲁棒性。

---

六、小结一句话

EasyEnsemble = 多次欠采样 + 集成学习。
它不创造数据，而是通过“多次利用数据”提升少数类识别能力，
是一种高效、稳健、实用的应对类不平衡的集成算法。

---

案例

EasyEnsemble、AdaBoost、SMOTE+随机森林（SMOTE+RF） 三种方法

---

一、对比目标

我们将比较三种模型的表现（主要看 少数类 Recall、F1-score）：

模型名称	方法类型	主要思想
AdaBoost	普通集成模型	不考虑类别不平衡
SMOTE + 随机森林	过采样 + 集成	通过SMOTE合成样本平衡数据
EasyEnsembleClassifier	欠采样 + 集成	多次随机欠采样 + AdaBoost 集成

---

二、完整 Python 实战代码

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier, RandomForestClassifier
from sklearn.metrics import classification_report
from imblearn.ensemble import EasyEnsembleClassifier
from imblearn.over_sampling import SMOTE
from collections import Counter# 1️⃣ 生成一个严重不平衡的数据集
X, y = make_classification(n_samples=3000, n_features=10,n_informative=6, n_redundant=2,n_classes=2, weights=[0.95, 0.05],  # 极度不平衡random_state=42
)
print("原始类别分布：", Counter(y))# 2️⃣ 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=42
)# ------------------ 模型①：普通 AdaBoost ------------------
ada = AdaBoostClassifier(n_estimators=100, random_state=42)
ada.fit(X_train, y_train)
y_pred_ada = ada.predict(X_test)
print("\n【AdaBoost】分类报告：")
print(classification_report(y_test, y_pred_ada, digits=3))# ------------------ 模型②：SMOTE + 随机森林 ------------------
smote = SMOTE(random_state=42)
X_train_sm, y_train_sm = smote.fit_resample(X_train, y_train)
print("SMOTE后类别分布：", Counter(y_train_sm))rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X_train_sm, y_train_sm)
y_pred_rf = rf.predict(X_test)
print("\n【SMOTE + 随机森林】分类报告：")
print(classification_report(y_test, y_pred_rf, digits=3))# ------------------ 模型③：EasyEnsemble ------------------
eec = EasyEnsembleClassifier(n_estimators=10,  # 集成的子模型数量random_state=42
)
eec.fit(X_train, y_train)
y_pred_eec = eec.predict(X_test)
print("\n【EasyEnsemble】分类报告：")
print(classification_report(y_test, y_pred_eec, digits=3))

---

三、示例结果（可能略有浮动）

假设输出如下（随机数据示例）：

【AdaBoost】

precision    recall  f1-score   support
0      0.97     1.00     0.99       855
1      0.75     0.18     0.29        45

【SMOTE + 随机森林】

precision    recall  f1-score   support
0      0.99     0.97     0.98       855
1      0.65     0.73     0.69        45

【EasyEnsemble】

precision    recall  f1-score   support
0      0.97     0.97     0.97       855
1      0.68     0.78     0.73        45

---

四、结果对比分析

模型	少数类 Recall	少数类 Precision	少数类 F1	说明
AdaBoost	0.18	0.75	0.29	传统方法，几乎忽略少数类
SMOTE + 随机森林	0.73	0.65	0.69	通过合成样本改善了识别能力
EasyEnsemble	0.78	0.68	0.73	表现最优，稳定识别少数类

---

五、总结对比

特点	AdaBoost	SMOTE+RF	EasyEnsemble
核心思想	权重提升，未考虑不平衡	过采样平衡数据	多次欠采样 + 集成
是否合成数据	否	是	否
少数类识别能力	弱	较好	最好
对极端不平衡数据适应性	差	中	强
训练时间	快	中等	稍慢（多模型）

结论：

• AdaBoost：适合数据较平衡场景；
• SMOTE + RF：适合中度不平衡；
• EasyEnsemble：在极度不平衡情况下表现最稳健，少数类 Recall 最高。

---

六、一句话总结

EasyEnsemble 是处理极度类不平衡问题的强力武器：
它通过多次欠采样 + 集成学习，
避免了过采样的噪声问题，同时最大限度利用多数类样本。

---