跳表(Skiplist)深度解析:从原理到手写hpp实现,清晰易懂
文章目录
- 一、跳表的结构
- 二、跳表的优化策略
- 1. 分层索引:模拟二分查找
- 2. 随机层数:平衡空间时间
- 三、跳表的时间复杂度
- 1. 随机层数的概率模型
- 2. 期望层数与空间复杂度
- 3. 查找的时间复杂度
- 四、跳表的C++实现
- 1. 跳表节点类(`SkiplistNode`)
- 2. 跳表类(`Skiplist`)与构造函数
- 3. 随机层数生成(`RandomLevel`)
- 4. 前驱节点查找(`FindPrevNodes`)
- 5. 查找操作(`search`)
- 6. 插入操作(`add`)
- 7. 删除操作(`erase`)
- 8. 打印操作(`Print`)
- 五、数据结构大擂台
在数据结构领域,平衡搜索树(AVL、红黑树)和哈希表常被用于解决查找问题,但前者实现复杂、后者无法有序遍历。有没有一种结构能兼顾 “高效查找”“有序遍历” 和 “简单实现”?答案是
跳表(Skiplist) 。跳表本质是一种高效查找结构,用于解决
key 或
key/value 的查找问题,与平衡搜索树、哈希表的核心价值一致,但设计思路更巧妙。它由
William Pugh于 1990 年在论文
《Skip Lists: A Probabilistic Alternative to Balanced Trees》中提出,(
阅读原文)。
一、跳表的结构
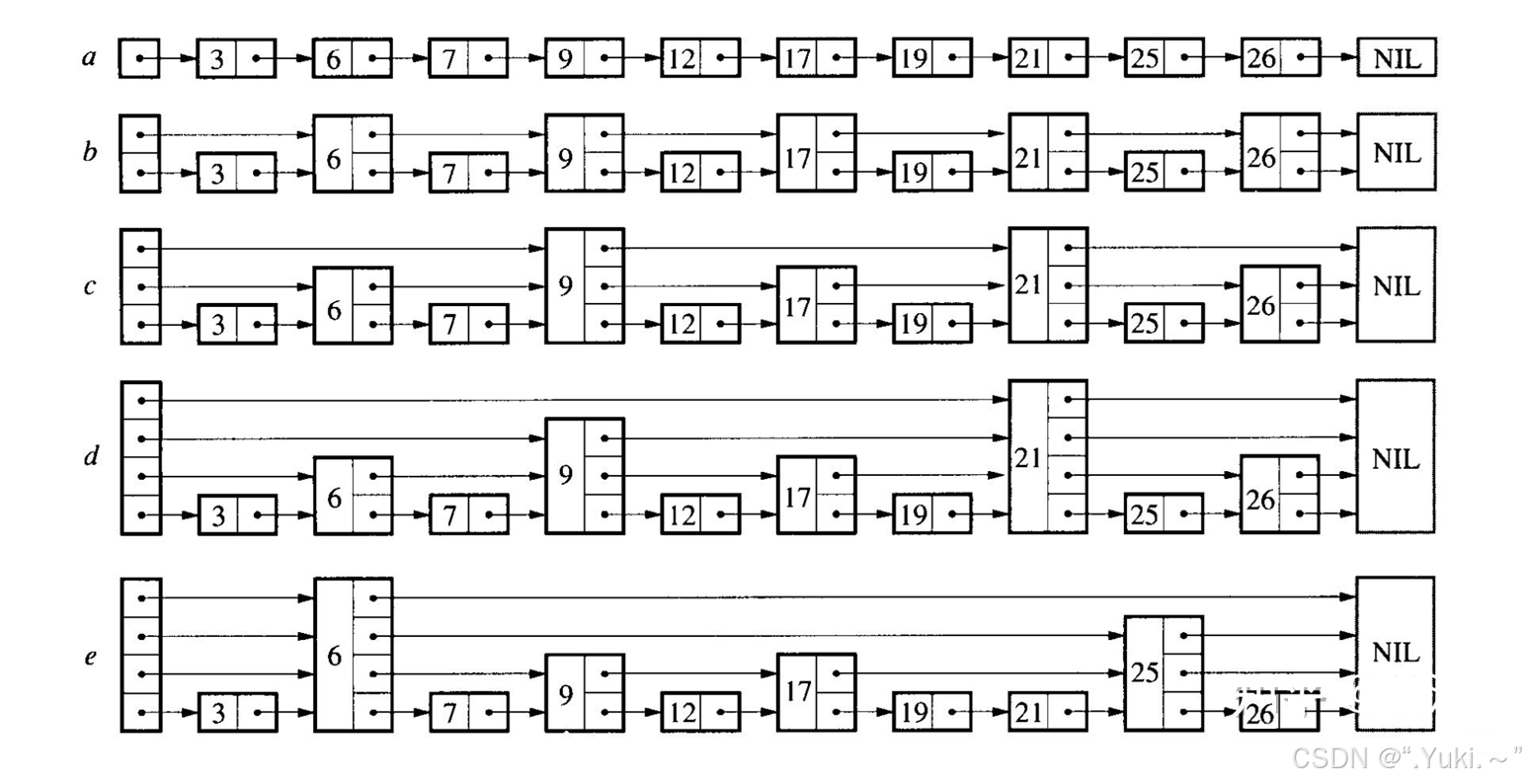
有序链表(如图1中的子图a)是最基础的有序数据结构:节点按值从小到大依次链接,插入/删除时只需调整相邻指针,但查找操作的时间复杂度为 ( O(n) )——要找一个元素,必须从表头开始逐个比较,直到找到目标或遍历结束,效率极低。
跳表则通过分层索引的思路彻底优化了这一问题。观察示意图(从子图b到e):
- 底层:是包含所有节点的“原始链表”(与普通有序链表一致);
- 上层:是“稀疏索引层”——每一层仅保留底层的部分节点,且上层节点数远少于下层(比如子图
b的上层索引间隔约2个节点,子图c的上层间隔更大); - 垂直链接:每一层的节点会通过指针链接到下一层的对应节点,形成“多层跳转”的结构。
优化核心:用“空间换时间”,通过多层索引减少查找时的比较次数。例如要找值为17的节点,可先在最上层索引快速定位到小于17的最近节点(如9),再下到下一层继续查找,无需遍历底层所有节点。
二、跳表的优化策略
有序链表的查找是线性扫描,而跳表的优化策略可总结为两点:
1. 分层索引:模拟二分查找
二分查找的核心是“每次排除一半元素”,跳表通过“多层索引”模拟这一过程:
- 最上层索引最稀疏,能快速跳过大量无关节点;
- 每下一层,索引密度增加,逐步缩小查找范围;
- 最终在
底层(全量节点层)完成精确匹配。
以示意图中查找17为例:
- 先在最顶层(如子图
e的顶层)快速定位到接近17的节点(比如通过顶层指针直接跳过3、6等早期节点); - 再下到中间层,进一步缩小范围;
- 最后在底层精准找到
17。
整个过程的比较次数从 ( O(n) ) 降到了 ( O(log n) ) 量级。
2. 随机层数:平衡空间时间
如果严格要求“上层节点数是下层的 ( 1/k )(如 ( 1/2 ))”,插入/删除节点时需要调整大量索引,复杂度会退化为 ( O(n) )。跳表的关键创新是:插入节点时,随机生成该节点的“层数”,不强制严格的层级比例。
这样做的好处是:插入/删除时无需调整其他节点的层级,实现简单;同时通过概率保证“大部分节点层数低,少数节点层数高”,依然能维持 ( O(log n) ) 的查找效率。
三、跳表的时间复杂度
跳表的时间复杂度分析核心是“证明查找操作的平均比较次数为 ( O(log n) )”,需从随机层数的概率分布和每层的查找成本两方面推导。
1. 随机层数的概率模型
定义两个关键参数:
- ( p ):
节点“向上延伸一层”的概率(通常取 ( p = 1/2 ) 或 ( p = 1/4 )); - ( L ):
节点的层数(至少为1)。
节点层数 ( L ) 的概率分布为:
![[ P(L = k) = (1 - p) \cdot p^{k - 1} ]](https://i-blog.csdnimg.cn/direct/8ee995325e0543f9ad592661631f0e6a.png)
节点“恰好有 k 层”意味着前 ( k-1 ) 次都“向上延伸”(概率 ( p )),第 ( k ) 次“不延伸”(概率 ( 1 - p ))。
2. 期望层数与空间复杂度
节点的期望层数 ( E[L] ) 为:
![[
E[L] = \sum_{k=1}^{\infty} k \cdot (1 - p) \cdot p^{k - 1}
]
这是“](https://i-blog.csdnimg.cn/direct/368378c0122d41d7bd89d6817a010f2c.png)
几何分布的期望”,计算得
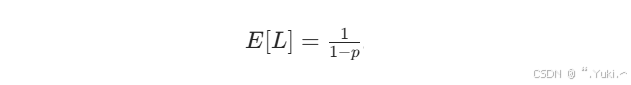
当 ( p = 1/2 ) 时,( E[L] = 2 )——即每个节点平均有2层;当 ( p = 1/4 ) 时,( E[L] = 1.33 )。因此,跳表的空间复杂度为 ( O(n * E[L]) = O(n) ),仅比普通链表多少量指针开销。
3. 查找的时间复杂度
查找时,每一层最多比较两次(“向右找”和“向下找”),而层数的期望为 ( O(log n) )(由随机层数的概率保证,可通过鞅论或递归分析证明,最终推导得平均查找次数为 ( O(log n) ))。
综上,跳表的查找、插入、删除操作的平均时间复杂度均为 ( O(log n) )。
四、跳表的C++实现
1. 跳表节点类(SkiplistNode)
class SkiplistNode {
public:int _val; // 节点存储的值std::vector<SkiplistNode*> _nextVec; // 各层的“下一个节点”指针// 构造函数:初始化值和层数,所有层级的后继初始为nullptrSkiplistNode(int val, int level) : _val(val) {_nextVec.resize(level, nullptr);}
};
- 功能:定义跳表的节点结构,用
_nextVec存储该节点在每一层的后继节点指针。 - 关键:
_nextVec的大小由节点的“层数”决定,初始化时所有层级的后继均为nullptr。
2. 跳表类(Skiplist)与构造函数
class Skiplist {
private:SkiplistNode* _head; // 头节点(哨兵节点,值为-1,简化边界判断)size_t _maxLevel; // 节点最大层数(参考Redis设为32,避免极端情况)double _probability; // 节点“升层”的概率(参考Redis设为0.25)std::mt19937 _rng; // 随机数生成器(生成更均匀的随机数)public:// 构造函数:初始化头节点、随机数生成器、默认参数Skiplist() : _maxLevel(32), _probability(0.25) {_head = new SkiplistNode(-1, 1); // 头节点初始层数为1// 用系统时间初始化随机数生成器_rng = std::mt19937(std::chrono::system_clock::now().time_since_epoch().count());}
};
- 功能:初始化跳表的核心组件。
- 关键:
- 头节点(
_head)是“哨兵节点”,值为-1,初始层数为1(后续会动态扩容); - 用
std::mt19937生成更均匀的随机数,为RandomLevel提供种子; _maxLevel限制节点最大层数,_probability控制节点“升层”的概率。
- 头节点(
3. 随机层数生成(RandomLevel)
int RandomLevel() {int level = 1;// 生成[0,1)的均匀分布随机数std::uniform_real_distribution<double> dist(0.0, 1.0);// 若随机数小于_probability且未超_maxLevel,层数+1while (dist(_rng) < _probability && level < _maxLevel) {++level;}return level;
}
- 功能:为新插入的节点生成随机层数。
- 逻辑:
- 初始层数为1;
- 每次生成
[0,1)的随机数,若小于_probability且未超过_maxLevel,则层数加1; - 最终层数符合“层数越高,概率越低”的分布(与前文数学模型一致)。
4. 前驱节点查找(FindPrevNodes)
std::vector<SkiplistNode*> FindPrevNodes(int num) {// 前驱数组:长度为_maxLevel,初始全为头节点std::vector<SkiplistNode*> prevVec(_maxLevel, _head);SkiplistNode* cur = _head;// (从跳表当前最大层数开始)int currentLevel = _head->_nextVec.size() - 1;while (currentLevel >= 0) {// 1:当前层后继存在且值小于num → 向右走if (cur->_nextVec[currentLevel] != nullptr && cur->_nextVec[currentLevel]->_val < num) {cur = cur->_nextVec[currentLevel];} // 2:当前层后继为空或值≥num → 记录前驱,向下走else {prevVec[currentLevel] = cur;--currentLevel;}}return prevVec;
}
- 功能:找到“各层中,值小于
num的最后一个节点”(即插入/删除时的“前驱节点”)。 - 实现:
- 从当前最大层数(头节点的
_nextVec长度-1)开始,逐层向下遍历; - 若当前层后继节点存在且值小于
num,则“向右走”;否则,记录当前节点为前驱,“向下走”; - 最终返回各层的前驱节点数组
prevVec,为后续插入/删除做准备。
- 从当前最大层数(头节点的
5. 查找操作(search)
bool search(int target) {SkiplistNode* cur = _head;// 当前遍历的层级(从跳表当前最大层数开始)int currentLevel = _head->_nextVec.size() - 1;while (currentLevel >= 0) {// 1:当前层后继存在且值小于target → 向右走if (cur->_nextVec[currentLevel] != nullptr && cur->_nextVec[currentLevel]->_val < target) {cur = cur->_nextVec[currentLevel];} // 2:当前层后继为空或值大于target → 向下走else if (cur->_nextVec[currentLevel] == nullptr || cur->_nextVec[currentLevel]->_val > target) {--currentLevel;} // 3:找到目标值 → 返回trueelse {return true;}}// 遍历完所有层仍未找到 → 返回falsereturn false;
}
- 功能:判断
target是否存在于跳表中。 - 实现:
- 从顶层开始,按“先右后下”的规则遍历;
- 若当前层后继节点值小于
target,向右走;若大于target,向下走;若等于target,返回true; - 遍历完所有层仍未找到,返回
false。
6. 插入操作(add)
void add(int num) {// 获取各层前驱节点std::vector<SkiplistNode*> prevVec = FindPrevNodes(num);// 生成新节点的随机层数int newLevel = RandomLevel();// 若新层数超过头节点当前层数,扩容头节点和前驱数组if (newLevel > _head->_nextVec.size()) {_head->_nextVec.resize(newLevel, nullptr);prevVec.resize(newLevel, _head);}// 创建新节点(值为num,层数为newLevel)SkiplistNode* newNode = new SkiplistNode(num, newLevel);// 遍历新节点的所有层级,完成插入(调整前驱和新节点的指针)for (int i = 0; i < newLevel; ++i) {newNode->_nextVec[i] = prevVec[i]->_nextVec[i]; // 新节点的后继 = 前驱的原后继prevVec[i]->_nextVec[i] = newNode; // 前驱的后继 = 新节点}
}
- 功能:将
num插入跳表,保持有序性。 - 实现:
- 用
FindPrevNodes获取各层前驱节点; - 生成新节点的随机层数
newLevel; - 若
newLevel超过头节点当前层数,扩容头节点的_nextVec和前驱数组; - 创建新节点,并遍历其所有层级,将新节点“插入”到各层前驱节点之后(调整前驱和新节点的
_nextVec指针)。
- 用
7. 删除操作(erase)
bool erase(int num) {// 获取各层前驱节点std::vector<SkiplistNode*> prevVec = FindPrevNodes(num);// 检查第0层(全量层)的后继是否为numSkiplistNode* delNode = prevVec[0]->_nextVec[0];if (delNode == nullptr || delNode->_val != num) {return false; // num不存在,删除失败}// 遍历待删除节点的所有层级,调整前驱指针(跳过delNode)for (size_t i = 0; i < delNode->_nextVec.size(); ++i) {prevVec[i]->_nextVec[i] = delNode->_nextVec[i];}// 释放待删除节点的内存delete delNode;// 收缩头节点的层数(若最高层无节点,减少_maxLevel)int currentMaxLevel = _head->_nextVec.size() - 1;while (currentMaxLevel >= 0 && _head->_nextVec[currentMaxLevel] == nullptr) {--currentMaxLevel;}_head->_nextVec.resize(currentMaxLevel + 1);return true;
}
- 功能:删除跳表中的
num(若存在)。 - 实现:
- 用
FindPrevNodes获取各层前驱节点; - 检查第0层(全量层)的后继是否为
num:若不是,返回false; - 遍历待删除节点的所有层级,将各层前驱节点的
_nextVec指针“跳过”待删除节点; - 释放待删除节点内存;
- 收缩头节点的层数(若最高层无节点,减少
_maxLevel,避免空层浪费)。
- 用
8. 打印操作(Print)
void Print() {// 获取总层数int totalLevel = _head->_nextVec.size();std::cout << "=== Skiplist(共" << totalLevel << "层)===" << std::endl;// 从顶层到底层打印各层结构for (int i = totalLevel - 1; i >= 0; --i) {std::cout << "Level " << i << ": ";SkiplistNode* cur = _head->_nextVec[i];while (cur != nullptr) {std::cout << cur->_val << " -> ";cur = cur->_nextVec[i];}std::cout << "NULL" << std::endl;}std::cout << "==========================" << std::endl;
}
- 从顶层到底层,逐层遍历并打印节点值,直到
nullptr(层的末尾)。
五、数据结构大擂台
| 特性/数据结构 | 跳表 | B树 | 哈希表 | 平衡二叉搜索树(红黑树为代表) |
|---|---|---|---|---|
| 查找时间复杂度 | 平均 ( O(\log n) ),最坏 ( O(n) )(极端随机情况概率极低) | ( O(\log_m n) )(( m ) 为B树阶数,通常较大,实际更高效) | 平均 ( O(1) ),最坏 ( O(n) )(哈希冲突严重时) | ( O(log n) )(严格保证) |
| 插入时间复杂度 | 平均 ( O(log n) ),最坏 ( O(n) ) | ( O(log_m n) ) | 平均 ( O(1) ),最坏 ( O(n) ) | ( O(log n) ) |
| 删除时间复杂度 | 平均 ( O(log n) ),最坏 ( O(n) ) | ( O(log_m n) ) | 平均 ( O(1) ),最坏 ( O(n) ) | ( O(log n) ) |
| 有序遍历支持 | 是(逐层遍历可高效合并有序序列) | 是(通过中序遍历变体实现有序遍历) | 否(哈希映射无天然顺序) | 是(中序遍历可得到有序序列) |
| 空间复杂度 | ( O(n) )(平均每个节点含 ( 2\sim1.33 ) 个指针,依“升层概率”而定) | ( O(n) )(每个节点存储多键+多子节点指针) | ( O(n) )(哈希桶+键值对存储) | ( O(n) )(每个节点含子节点指针、颜色标记等) |
