【算法】day8 二分查找+前缀和

1、搜索旋转排序数组 hot

题目：33. 搜索旋转排序数组 - 力扣（LeetCode）

分析：

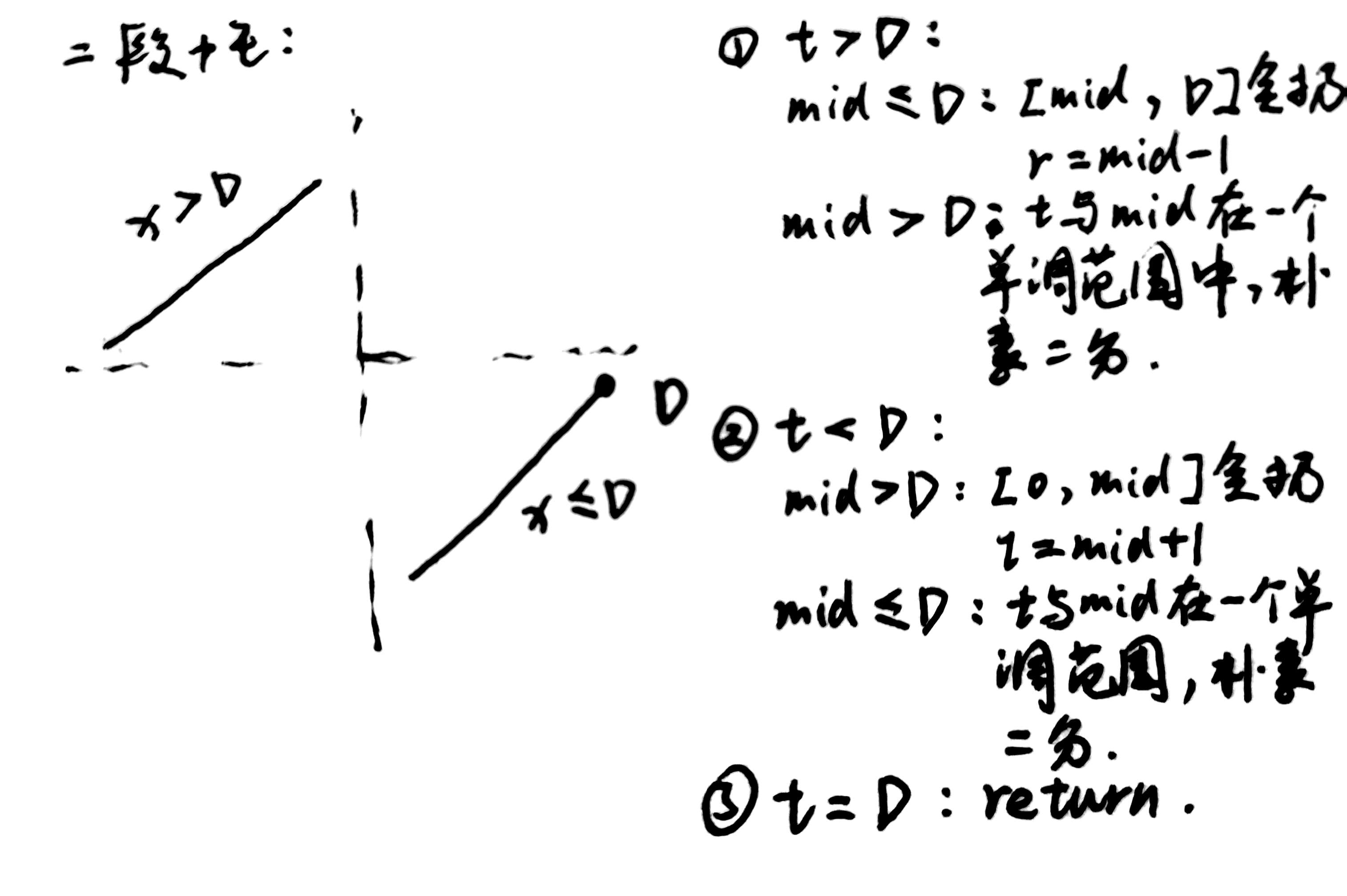
代码：

class Solution {public int search(int[] nums, int target) {int left=0, right=nums.length-1;while(left <= right) {int tmp = nums[right];int mid = left+(right-left)/2;if (target > tmp) {if (nums[mid] <= tmp) right = mid-1;else {if (nums[mid] < target) left = mid+1;else if (nums[mid] > target) right = mid-1;else return mid;}} else if (target < tmp) {if (nums[mid] > tmp) left = mid+1;else {if (nums[mid] < target) left = mid+1;else if (nums[mid] > target) right = mid-1;else return mid;}} else return right;}return -1;}
}

2、寻找两个正序数组的中位数 hot

题目：4. 寻找两个正序数组的中位数 - 力扣（LeetCode）

分析：看时间复杂度，二分查找。

• 转换思路：找第 k 小的数字。m+n为奇数，找第 (m+n)/2+1 小；m+n为偶数，找第 (m+n)/2 和 (m+n)/2+1 小的平均。
• 每次比较两个数组剩下的第 k/2 个数，较小的及其前面的数必定不是第 k 小，删除这 k/2 个数，更新 k 值。
• 直到 k=1，为两个数组的较小的第一个数。
• 也有可能其中一个数组先删完了，就返回另一个数组的第 k 个数。 

代码：

class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {// 如果是奇数，找第 (len1+len2)/2+1 小// 如果是偶数，找第 (len1+len2)/2 小和第 (len1+len2)/2+1，计算均值int len = nums1.length + nums2.length;if (len % 2 == 1) return getKthMin(nums1, nums2, len/2+1);else return (getKthMin(nums1, nums2, len/2) + getKthMin(nums1, nums2, len/2+1))/2.0;}public int getKthMin(int[] nums1, int[] nums2, int k) {int index1 = 0, index2 = 0; // 两个数组现在待处理的元素下标int len1 = nums1.length, len2 = nums2.length; while(true) {// 数组1先删完了，返回数组2的第 k 小数if (index1 == len1) return nums2[index2+k-1];// 数组2先删完了，返回数组1的第 k 小数if (index2 == len2) return nums1[index1+k-1];// 数组1和2都还没有删完，但是查找第 k=1 小，返回两个数组第一个数较小的if (k == 1) return Math.min(nums1[index1], nums2[index2]);// 正常情况// 删除两个数组中，第 k/2 小数较小的数，及其前 k/2-1 个数，这 k/2 个数必定不是第 k 小数// 有可能数组剩余长度比 k/2 小，这时比较数组最后一个数即可int newIndex1 = Math.min(len1-1, index1+k/2-1);int newIndex2 = Math.min(len2-1, index2+k/2-1); // 删除前更新 kif (nums1[newIndex1] <= nums2[newIndex2]) {k -= newIndex1-index1+1;index1 = newIndex1+1;}else {k -= newIndex2-index2+1;index2 = newIndex2+1;}}}
}

3、前缀和

题目：【模板】前缀和_牛客题霸_牛客网

分析：

① 暴力解法：q 次查询，每次查询挨个计算和，求和最坏遍历 n 个元素。时间复杂度：O(nq)

② 前缀和（动态规划）：快速求出数组中某一个连续区间的和。

第一步：构造前缀和数据。i 不能从 0 开始，因为无法获取 dp[-1]，这样还得单独判断。i 从 1 开始，获取的 dp[0] 初始化就是 0，对计算没影响。时间复杂度 O(n)

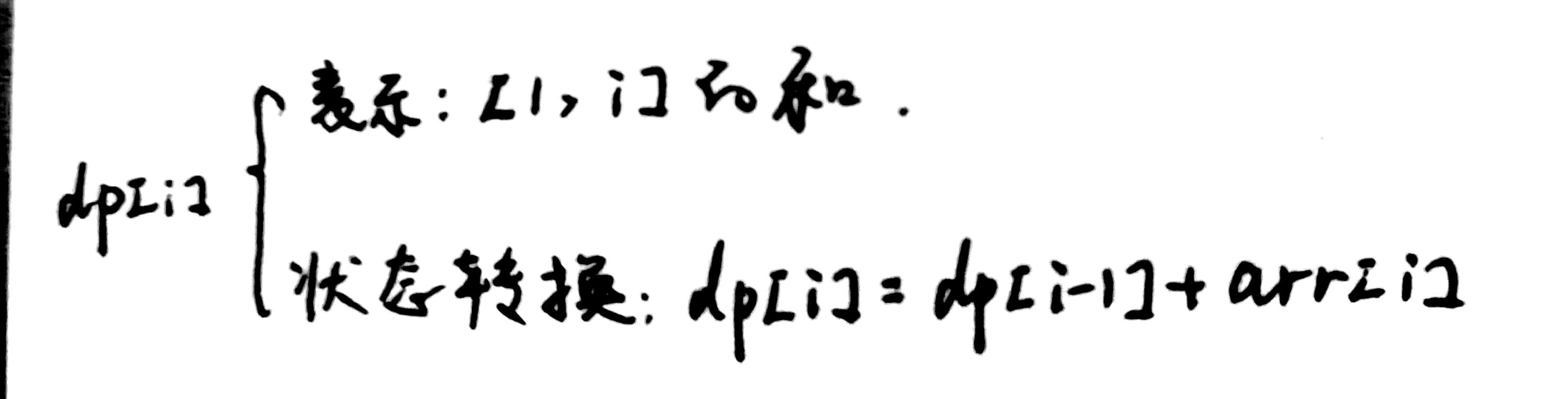
第二步：使用前缀和数组。 时间复杂度 O(1)

[l, r] 连续子数组之和 = dp[r] - dp[l-1]

查询 q 次，时间复杂度：O(n+q)。

代码：注意，和可能会超出 int 的返回，因此 dp 数组元素类型为 long。

import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextInt()) {int n = in.nextInt();int q = in.nextInt();// 接收数组int[] arr = new int[n+1];// 构造前缀和数组long[] dp = new long[n+1];for(int i = 1; i <= n; i++) {arr[i] = in.nextInt();dp[i] = dp[i-1]+arr[i];}// 接收 q 次查询for(int i = 0; i < q; i++) {int l = in.nextInt();int r = in.nextInt();System.out.println(dp[r] - dp[l-1]);}}}
}

4、二维前缀和

题目：【模板】二维前缀和_牛客题霸_牛客网

分析：

① 暴力解法：询问 q 次，每次最坏遍历 mn 个元素求和。时间复杂度 O(qmn)。

② 前缀和：

第一步：构造前缀和数组。

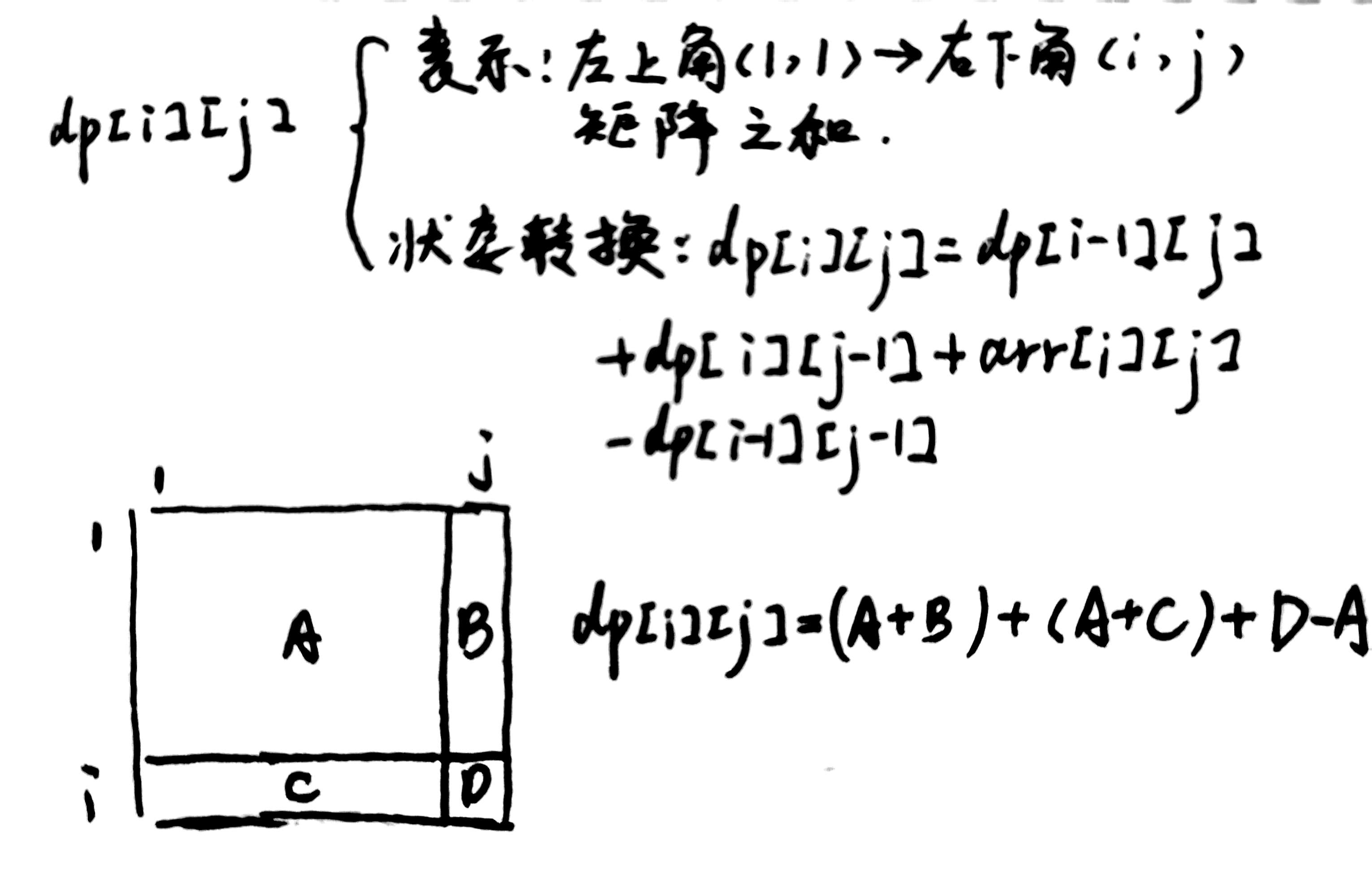
第二部：使用前缀和数组。

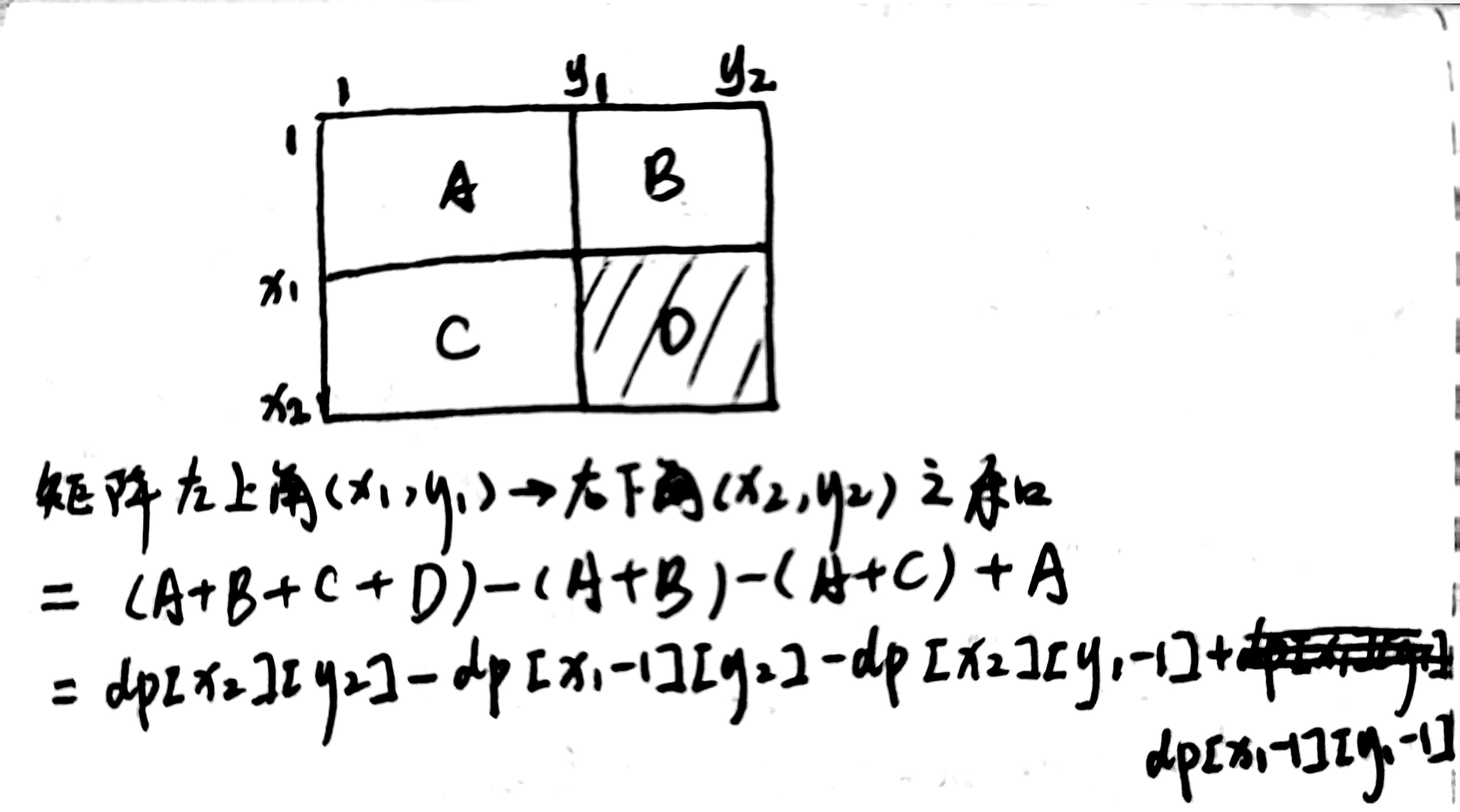
代码：

import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint n = in.nextInt();int m = in.nextInt();int q = in.nextInt();// 接收矩阵int[][] matrix = new int[n+1][m+1];// 构造前缀和矩阵long[][] dp = new long[n+1][m+1];for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++) {matrix[i][j] = in.nextInt();dp[i][j] = dp[i-1][j] + dp[i][j-1] + matrix[i][j] - dp[i-1][j-1];}// q 次查询for(int i = 0; i < q; i++) {int x1 = in.nextInt();int y1 = in.nextInt();int x2 = in.nextInt();int y2 = in.nextInt();System.out.println(dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]); }}}
}