当前位置：首页 > news >正文

[排序算法]希尔排序

news 2025/10/20 7:24:29

前言

希尔排序是对直接插入排序的优化，其思路是先创造“基本有序”的条件，再进行精细的插入排序。

如果你还没有学会直接插入排序算法，那请先看博主前一篇文章：[排序算法]直接插入排序。

学完直接插入排序，我们不难得出其优缺点：

优点：当待排序序列基本有序时，直接插入排序的效率非常高，近似 O(n)。

缺点：当待排序序列完全逆序时，效率极低，为 O(n²)。因为每次插入一个新元素，都需要与前面所有已排序的元素进行比较和移动。

我们希尔排序就是为了降低缺点的影响，通过预处理，使待排序序列“基本有序”。

基本思想

希尔排序是对直接插入排序的优化，其核心思想是通过一个递减的步长序列（gap sequence）将数组分成若干子序列，对每个子序列进行插入排序，使数组逐渐“基本有序”，最后当步长为1时进行直接插入排序。这种预处理能有效减少直接插入排序中的比较和移动次数，从而提升整体效率。

有点懵？先不要慌！下面咱们逐步分析。

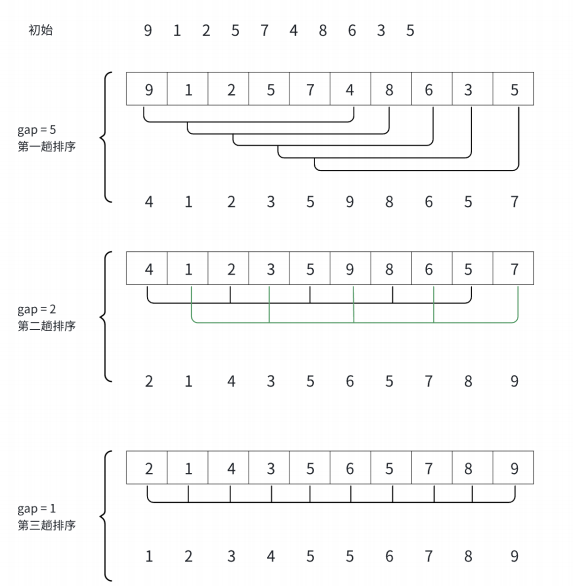
具体步骤：

选择一个初始步长gap（通常为n/2或n/3）。

将数组中间隔为gap的元素分在同一组，形成多个子序列。

对每个子序列进行插入排序。

缩小gap（例如，使用gap = gap / 3 + 1），重复步骤2-3，直到gap=1。

当gap=1时，执行一次直接插入排序，此时数组已基本有序，排序效率很高。

打个比方：

详解代码

//希尔排序
void ShellSort(int* a, int n)
{//gap是步长，gap的值就是每组数据间隔//比如第一组第一个数据为arr[i]那下一个即为arr[i+gap]int gap = n;while (gap > 1){//推荐写法：除3gap = gap / 3 + 1;//i如果大于等于n-gap，会导致a[end+gap]越界访问for (int i = 0; i < n - gap; i++){//从第一个元素开始//end含义为已排序部分的最后一个元素的下标int end = i;//tmp为该组下一个元素的值int tmp = a[end + gap];//end如果小于0，则证明a[end+gap]已经和该组第一个元素互换了值while (end >= 0){//同一组中，若前面的数大于后面的if (a[end] > tmp){//后面的值等于前面的a[end + gap] = a[end];//end自身减gapend -= gap;}//否则证明已经有序else{break;}}//两种情况，if满足一种，不满足一种a[end + gap] = tmp;}}
}

希尔排序的时间复杂度范围大致在 O(n log²n) 到 O(n²) 之间。通过选择优秀的增量序列，其平均时间复杂度可以优化到大约 O(n^1.3) 到 O(n^1.5)，这明显优于 O(n²) 的直接插入排序。

希尔排序时间复杂度不好计算，因为 gap 的取值很多，导致很难去计算，因此很多书中给出的希尔排序的时间复杂度都不固定。《数据结构(C语言版)》--- 严蔚敏书中给出的时间复杂度为：