算法代码速成8:非线性最小二乘问题编程示例:人口预测
上上篇(文章6算法代码讲座6:最小二乘法理论原理、典型案例与MATLAB实现)讲了最小二乘法的理论,其中一支为线性问题,另外一支为非线性问题,线性问题在前面的文章已有讲述,本文讲一下非线性的最小二乘问题。
1.概念
非线性最小二乘问题的基本假设:采样数据x和y呈非线性关系。
注:前面文章里所讲的线性问题求解方法,不再适用于非线性问题求解了。
2.数学模型
对于给定的采样数据点(x(i), y(i)), i=1,2,...,n,寻找函数f(x),使其最佳的逼近拟合采样数据。
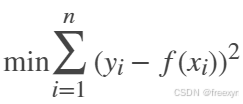
其中,函数f(x)为非线性方程形式,在求解时,需要根据实际问题的特性,对函数f(x)的表达式进行预估,在根据求解效果做适量修正。
3.非线性最小二乘问题:人口增长模型
根据经典的马尔萨斯人口模型,人口的增长是呈指数级的,于是,假设人口数量与时间的关系函数形式如下:
f(t)=p0ert
其中,p0是人口的初始值,r是增长率,t是时间。
统计1950~2000年人口数据如下表:
| 时间(年) | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
| 人口(亿) | 2.5 | 3 | 3.7 | 4.5 | 5.3 | 6.1 |
使用最小二乘法拟合并预测2000年~2020年的人口情况。
4.Matlab求解编程代码
% 人口数据
t= [1950, 1960, 1970, 1980, 1990, 2000];
y = [2.5, 3.0, 3.7, 4.5, 5.3, 6.1];
% 定义指数模型
exp_model = @(beta, t) beta(1) * exp(beta(2) * (t - 1950));
% 初始参数估计
beta0 = [y(1), 0.01]; % [p0, r]
% 使用lsqcurvefit求解
[beta, resnorm, residuals] = lsqcurvefit(exp_model, beta0, t, y)
运行结果:
可能存在局部最小值。
lsqcurvefit 已停止,因为平方和相对于其初始值的最终变化小于函数容差值。
<停止条件详细信息>
beta =
2.5794 0.0176
resnorm =
0.0504
residuals =
0.0794 0.0753 -0.0334 -0.1285 -0.0881 0.1138
%其中,beta为参数[p0, r]的最小二乘解,resnorm为残差,residuals为每个数据点的残差。
% 计算预测
t_pred = 1950:5:2020;
pop_pred = exp_model(beta, t_pred);
% 可视化结果
scatter(t, y, 100, 'filled', 'MarkerFaceColor', [0.9 0.3 0.2]);
hold on;
plot(t_pred, pop_pred, 'b-', 'LineWidth', 2);
xlabel('年份');
ylabel('人口 (亿)');
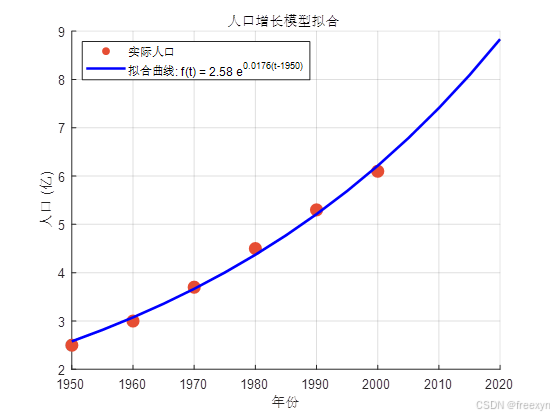
title('人口增长模型拟合');
legend('实际人口', sprintf('拟合曲线: f(t) = %.2f e^{%.4f(t-1950)}',...
beta(1), beta(2)), 'Location', 'northwest');
grid on;
运行结果:
% 计算统计指标
SSE = resnorm;
SST = sum((y - mean(y)).^2);
R_squared = 1 - SSE/SST
RMSE = sqrt(SSE/length(y))
运行结果:
R_squared =
0.9947
RMSE =
0.0916
相关视频内容推荐
46.1 LSTM序列数据预测(理论+程序可仿写)
37.21 Appdesigner实例:信息查询筛选导出系统
45.22 超简单玩转Matlab深度学习工具箱深度网络设计器
21.6 一维域外插值,使用interp1同时要设置一下参数
13.4 Matlab编程求导:雅可比矩阵
23.16 最小二乘法的概念:线性、加权、鲁棒、非线性最小二乘法及Matlab编程实例
24.2 KNN算法之邻点搜索方法:KD树,概念、原理和搜索流程KDTreeSearcher
25.2.1 朴素贝叶斯算法|原理篇:连续型数据分类识别
35.10 郑重其事的讲下:局部函数
44.6 非线性自回归神经网络narnet时序数据预测编程代码实例
38.4 从图片上自动提取圆心坐标和半径数据
26.5 SVM支持向量机,核函数Kernel和核变换,Matlab编程实例
66.58 更改三维图坐标标签的字体、字号和旋转角度
31.6 Matlab绘制条形图柱状图,改变单个柱的颜色,堆叠显示,改变线型线宽
66.38 一个Matlab优化程序纠错实例,这个简单
End
