AVL树(平衡二叉树)详细介绍与Java实现

AVL树(平衡二叉搜索树)

介绍

定义：

AVL树是一种自平衡二叉搜索树，其中每个节点的左右子树的高度差（平衡因子）最多为1。当插入或删除节点导致平衡因子绝对值大于1时，需要通过旋转来恢复平衡。

平衡二叉树是一种特殊的二叉搜索树，它通过自动调整树的结构来保持较低的高度，从而确保各种操作的高效性。

主要目标是避免BST退化为链表，保证操作时间复杂度为O(log n)。

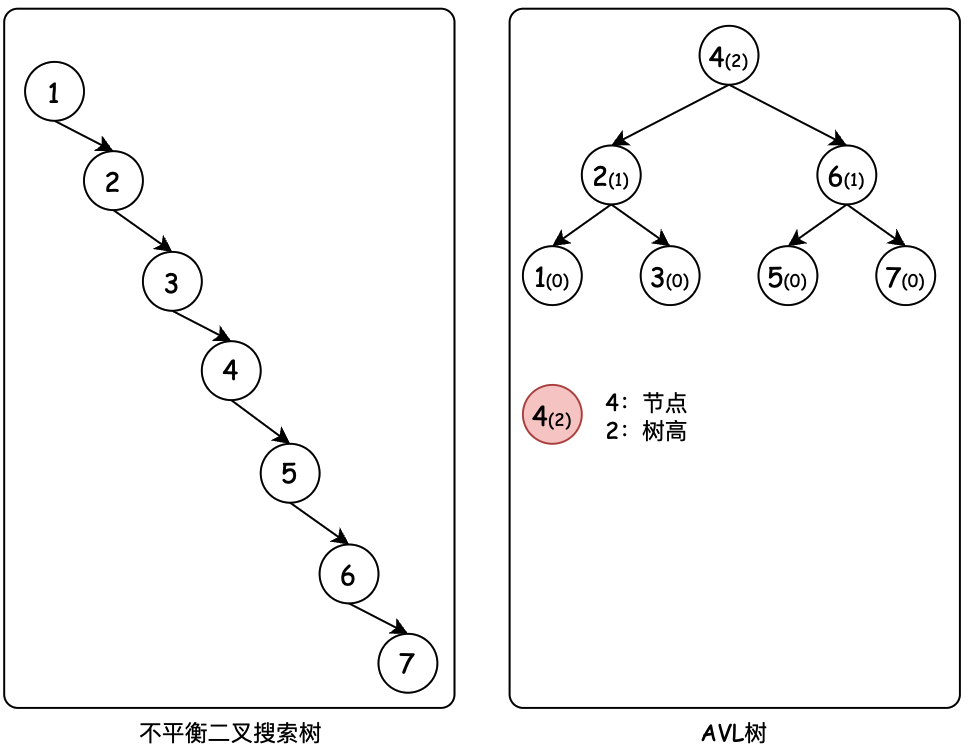
性质：

• 平衡因子：节点左子树高度 - 右子树高度，绝对值 ≤ 1
• 自平衡：插入/删除后自动调整结构恢复平衡
• 高度平衡：树的高度始终保持在O(log n)

Java实现

1. AVL树节点类

属性 ：val（节点值）、left（左子节点）、right（右子节点）、height（节点高度）

@Data
public class AVLNode {/** 节点值 */int val;/** 左子节点 */AVLNode left;/** 右子节点 */AVLNode right;/** 节点高度 */int height;/*** 构造函数* @param val 节点值*/public AVLNode(int val) {this.val = val;this.left = null;this.right = null;this.height = 1; // 新节点的高度为1}}

1. AVL树主类，实现核心功能主要方法 ：

• insert(int val) - 插入节点并自动平衡
• delete(int val) - 删除节点并自动平衡
• search(int val) - 查找节点
• inorder()/preorder() - 中序/前序遍历
• isBalanced() - 检查树是否平衡
• getHeight() - 获取树高度

public class AVLTree {/** 根节点 */private AVLNode root;/*** 构造函数，初始化空的AVL树*/public AVLTree() {this.root = null;}// ......
}

获取节点信息

/*** 获取节点的高度* 如果节点为空，返回0* @param node 要获取高度的节点* @return 节点的高度*/
private int height(AVLNode node) {if (node == null) {return 0;}return node.getHeight();
}/*** 获取节点的平衡因子* 平衡因子 = 左子树高度 - 右子树高度* @param node 要计算平衡因子的节点* @return 平衡因子*/
private int getBalance(AVLNode node) {if (node == null) {return 0;}return height(node.getLeft()) - height(node.getRight());
}/*** 更新节点的高度* 节点高度 = 1 + 左右子树高度的最大值* @param node 要更新高度的节点*/
private void updateHeight(AVLNode node) {if (node != null) {int leftHeight = height(node.getLeft());int rightHeight = height(node.getRight());node.setHeight(Math.max(leftHeight, rightHeight) + 1);}
}

⭐左旋leftRotate

左旋的作用：相当于通过向上迁移树高差大于1的右子节点来降低树高的操作。

如图所示：将y节点上迁移，将y节点的左指针指向x，再将x的右指针指向T2

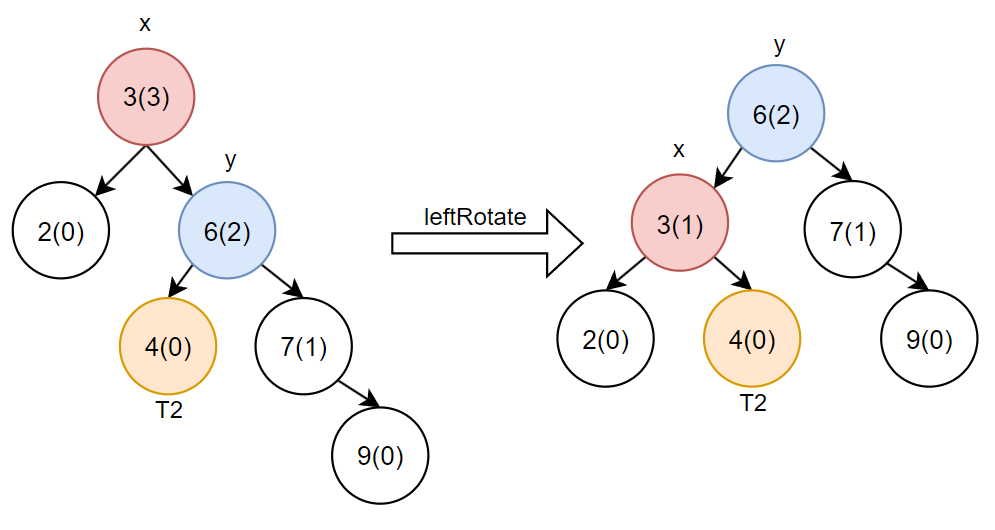
/*** 左旋操作（右右情况）* 用于处理右子树过高的不平衡情况* @param x 不平衡的节点* @return 旋转后的新根节点*/
private AVLNode leftRotate(AVLNode x) {AVLNode y = x.getRight();AVLNode T2 = y.getLeft();// 执行旋转y.setLeft(x);x.setRight(T2);// 更新高度updateHeight(x);updateHeight(y);return y;
}

⭐右旋rightRotate

右旋的作用：相当于通过向上迁移树高差大于1的左子节点来降低树高的操作。

如图所示：将x节点上迁移，将x节点的右指针指向y，再将y的左指针指向T2

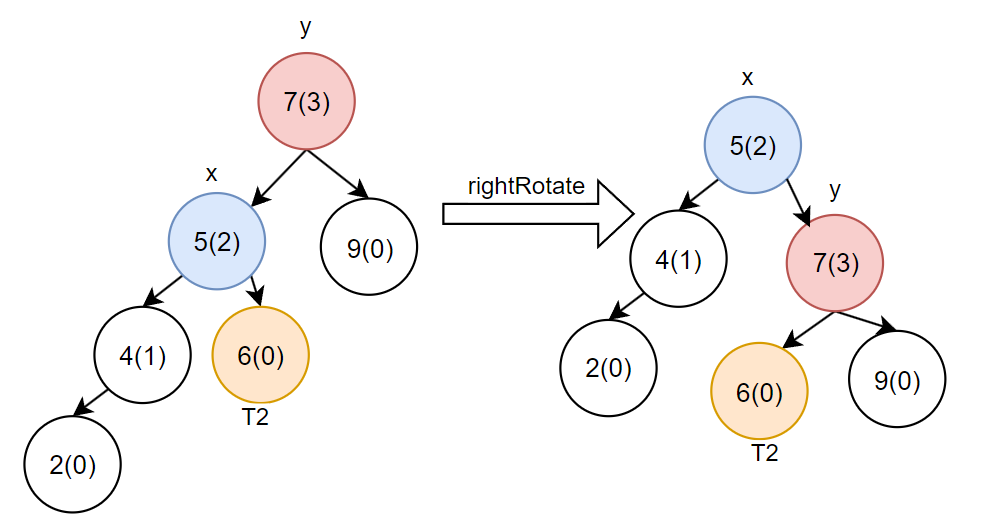
/*** 右旋操作（左左情况）* 用于处理左子树过高的不平衡情况* @param y 不平衡的节点* @return 旋转后的新根节点*/
private AVLNode rightRotate(AVLNode y) {AVLNode x = y.getLeft();AVLNode T2 = x.getRight();// 执行旋转x.setRight(y);y.setLeft(T2);// 更新高度updateHeight(y);updateHeight(x);return x;
}

⭐插入节点 insert

平衡因子 = 左子树高度 - 右子树高度

• 平衡因子 > 1：左子树过高（需要右旋）
• 平衡因子 < -1：右子树过高（需要左旋）

插入节点有4种情况：

1.1.1. 左左情况（LL - Left Left）

1. 触发条件 ： balance > 1 && val < node.getLeft().getVal()
2. 新节点插入到左子树的左子树中
3. 需要执行右旋操作

// 左左情况（左子树的左子树过高）
if (balance > 1 && val < node.getLeft().getVal()) {return rightRotate(node);
}

1.1.2. 右右情况（RR - Right Right）

1. 触发条件 ： balance < -1 && val > node.getRight().getVal()
2. 新节点插入到右子树的右子树中
3. 需要执行 左旋操作

// 右右情况（右子树的右子树过高）
if (balance < -1 && val > node.getRight().getVal()) {return leftRotate(node);
}

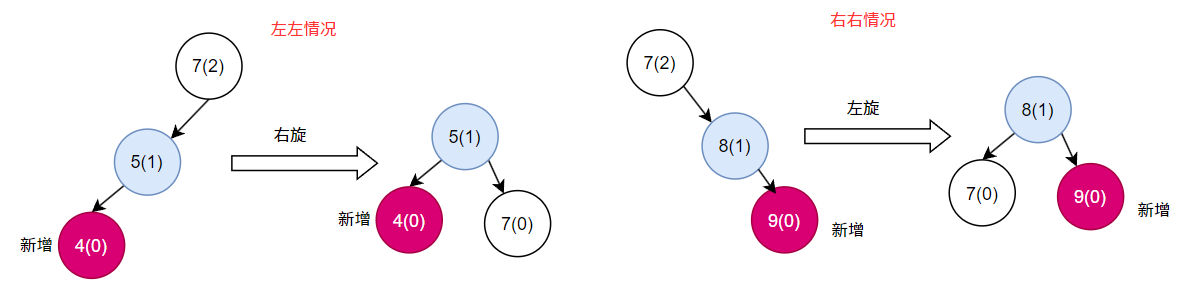
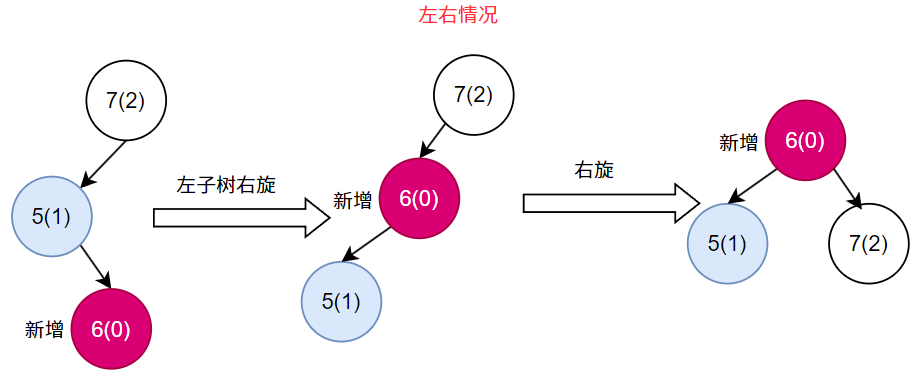
1.1.3. 左右情况（LR - Left Right）

1. 触发条件 ：balance > 1 && val > node.getLeft().getVal()
2. 新节点插入到左子树的右子树中
3. 需要先 左旋 再 右旋 （两步操作）

// 左右情况（左子树的右子树过高）
if (balance > 1 && val > node.getLeft().getVal()) {node.setLeft(leftRotate(node.getLeft()));  // 先对左子树左旋return rightRotate(node);                  // 再对当前节点右旋
}

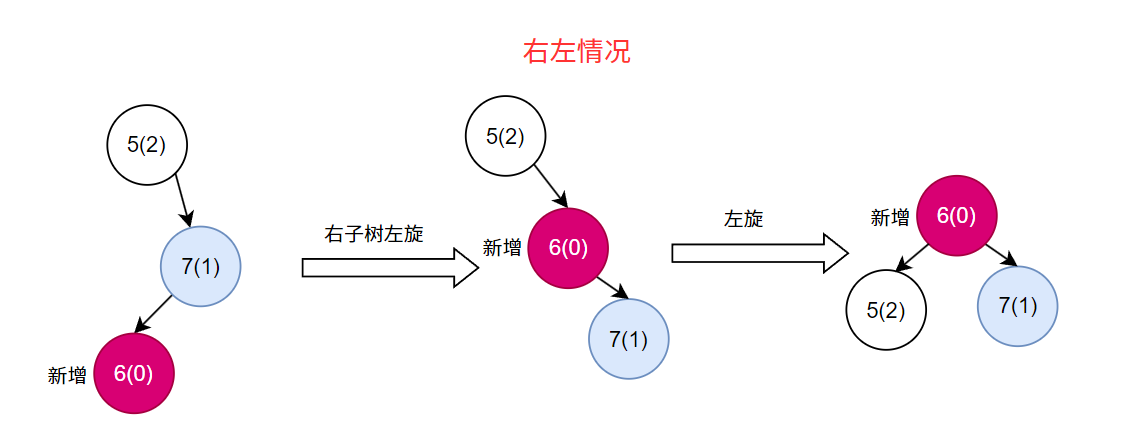
1.1.4. 右左情况（RL - Right Left）

1. 触发条件 ：balance < -1 && val < node.getRight().getVal()
2. 新节点插入到右子树的左子树中
3. 需要先 右旋 再 左旋 （两步操作）

// 右左情况（右子树的左子树过高）
if (balance < -1 && val < node.getRight().getVal()) {node.setRight(rightRotate(node.getRight())); // 先对右子树右旋return leftRotate(node);                     // 再对当前节点左旋
}

1.1.5. 完整代码演示

/*** 插入新节点到AVL树* @param val 要插入的值*/
public void insert(int val) {root = insert(root, val);
}/*** 递归插入新节点并保持平衡* @param node 当前节点* @param val 要插入的值* @return 插入后的节点*/
private AVLNode insert(AVLNode node, int val) {// 1. 执行标准的BST插入if (node == null) {return new AVLNode(val);}if (val < node.getVal()) {node.setLeft(insert(node.getLeft(), val));} else if (val > node.getVal()) {node.setRight(insert(node.getRight(), val));} else {// 不允许重复值return node;}// 2. 更新当前节点的高度updateHeight(node);// 3. 获取平衡因子检查是否平衡int balance = getBalance(node);// 4. 如果不平衡，有四种情况需要处理// 左左情况（左子树的左子树过高）if (balance > 1 && val < node.getLeft().getVal()) {return rightRotate(node);}// 右右情况（右子树的右子树过高）if (balance < -1 && val > node.getRight().getVal()) {return leftRotate(node);}// 左右情况（左子树的右子树过高）if (balance > 1 && val > node.getLeft().getVal()) {node.setLeft(leftRotate(node.getLeft()));return rightRotate(node);}// 右左情况（右子树的左子树过高）if (balance < -1 && val < node.getRight().getVal()) {node.setRight(rightRotate(node.getRight()));return leftRotate(node);}// 如果平衡，直接返回节点return node;
}

删除节点 delete

1.1.1. 删除叶子节点

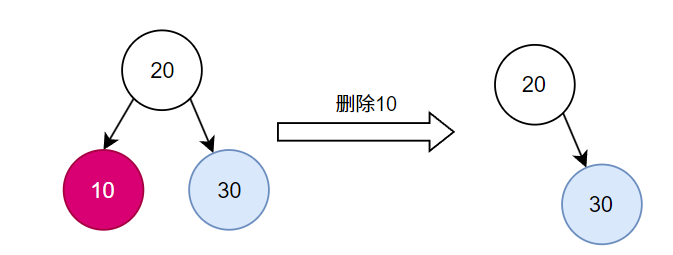
1.1.2. 删除有一个子节点的节点

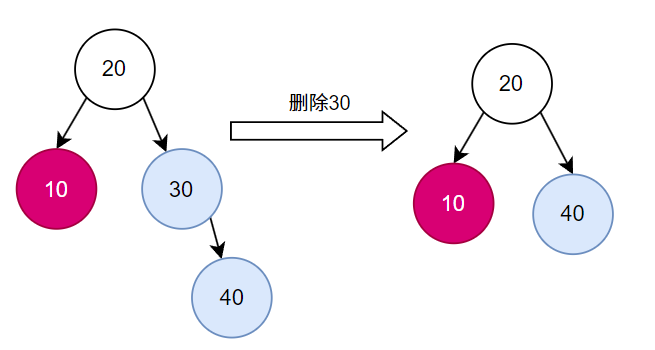
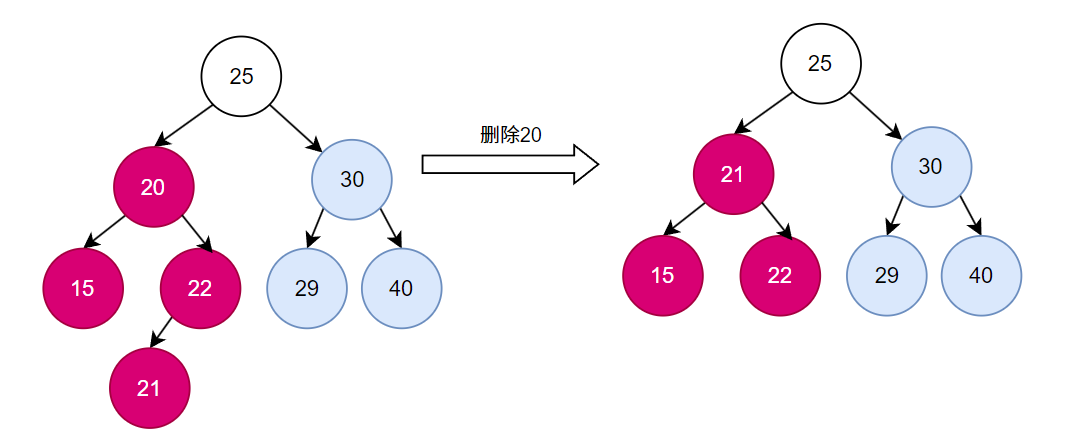
1.1.3. 删除有两个子节点的节点

用中序后继（右子树的最小值）替换被删除节点，然后删除中序后继

/*** 从AVL树中删除指定值的节点* @param val 要删除的值*/
public void delete(int val) {root = delete(root, val);
}/*** 递归删除节点并保持平衡* @param node 当前节点* @param val 要删除的值* @return 删除后的节点*/
private AVLNode delete(AVLNode node, int val) {// 1. 执行标准的BST删除if (node == null) {return null;}if (val < node.getVal()) {node.setLeft(delete(node.getLeft(), val));} else if (val > node.getVal()) {node.setRight(delete(node.getRight(), val));} else {// 找到要删除的节点// 节点只有一个子节点或没有子节点if (node.getLeft() == null || node.getRight() == null) {AVLNode temp = null;if (temp == node.getLeft()) {temp = node.getRight();} else {temp = node.getLeft();}// 没有子节点的情况if (temp == null) {temp = node;node = null;} else {// 有一个子节点的情况node = temp;}} else {// 节点有两个子节点：获取中序后继（右子树的最小值）AVLNode temp = minValueNode(node.getRight());node.setVal(temp.getVal());node.setRight(delete(node.getRight(), temp.getVal()));}}// 如果树只有一个节点，直接返回if (node == null) {return null;}// 2. 更新当前节点的高度updateHeight(node);// 3. 获取平衡因子检查是否平衡int balance = getBalance(node);// 4. 如果不平衡，有四种情况需要处理// 左左情况if (balance > 1 && getBalance(node.getLeft()) >= 0) {return rightRotate(node);}// 左右情况if (balance > 1 && getBalance(node.getLeft()) < 0) {node.setLeft(leftRotate(node.getLeft()));return rightRotate(node);}// 右右情况if (balance < -1 && getBalance(node.getRight()) <= 0) {return leftRotate(node);}// 右左情况if (balance < -1 && getBalance(node.getRight()) > 0) {node.setRight(rightRotate(node.getRight()));return leftRotate(node);}return node;
}

查找节点 search

/*** 查找子树中的最小值节点* @param node 子树根节点* @return 最小值节点*/
private AVLNode minValueNode(AVLNode node) {AVLNode current = node;while (current.getLeft() != null) {current = current.getLeft();}return current;
}/*** 在AVL树中查找指定值* @param val 要查找的值* @return 如果找到返回true，否则返回false*/
public boolean search(int val) {return search(root, val);
}/*** 递归查找指定值* @param node 当前节点* @param val 要查找的值* @return 如果找到返回true，否则返回false*/
private boolean search(AVLNode node, int val) {if (node == null) {return false;}if (val == node.getVal()) {return true;} else if (val < node.getVal()) {return search(node.getLeft(), val);} else {return search(node.getRight(), val);}
}

中序/前序遍历inorder()/preorder()

/*** 中序遍历AVL树* 对于AVL树，中序遍历会产生有序序列*/
public void inorder() {inorder(root);System.out.println();
}/*** 递归执行中序遍历* @param node 当前节点*/
private void inorder(AVLNode node) {if (node != null) {inorder(node.getLeft());System.out.print(node.getVal() + "(" + node.getHeight() + ") ");inorder(node.getRight());}
}/*** 前序遍历AVL树*/
public void preorder() {preorder(root);System.out.println();
}/*** 递归执行前序遍历* @param node 当前节点*/
private void preorder(AVLNode node) {if (node != null) {System.out.print(node.getVal() + "(" + node.getHeight() + ") ");preorder(node.getLeft());preorder(node.getRight());}
}

检查树是否平衡isBalanced()

/*** 递归检查子树是否平衡* @param node 当前节点* @return 如果平衡返回true，否则返回false*/
private boolean isBalanced(AVLNode node) {if (node == null) {return true;}int balance = getBalance(node);if (Math.abs(balance) > 1) {return false;}return isBalanced(node.getLeft()) && isBalanced(node.getRight());
}

获取树高度getHeight()

/*** 获取树的高度* @return 树的高度*/
public int getHeight() {return height(root);
}/*** 获取根节点* @return 根节点*/
public AVLNode getRoot() {return root;
}/*** 主方法，用于测试AVL树的功能* @param args 命令行参数*/