【Luogu】P1972 [SDOI2009] HH 的项链 (树状数组求区间内不同数的个数)

P1972 [SDOI2009] HH 的项链 - 洛谷

题目：

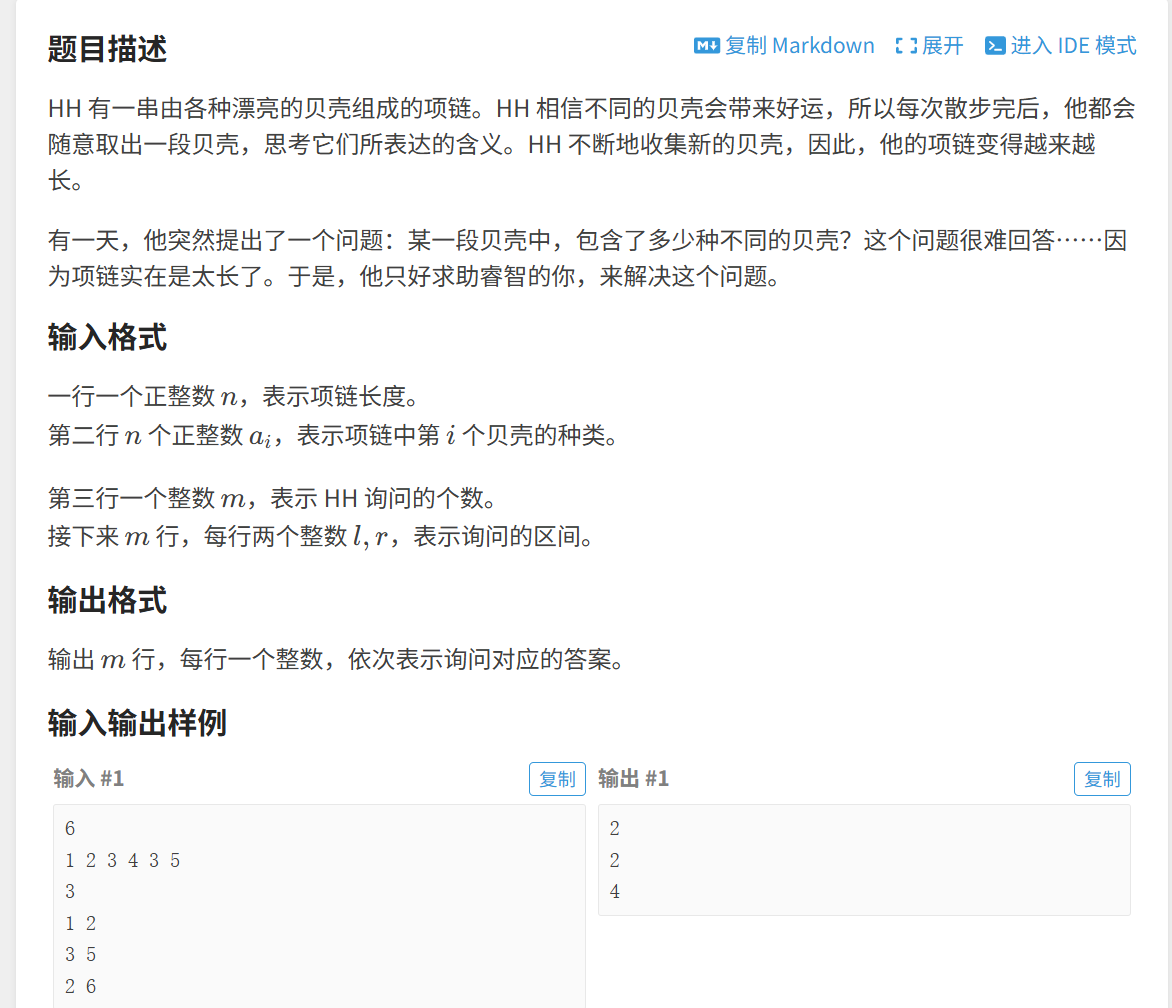
思路：

考虑如何维护区间内不同数个个数？

由于反复出现的数只算 1 的奉献，那么我们就只保留最右边的数的奉献。具体的，对于 1 2 1 2 3 这个数组，其权值数组 val 为 0 0 1 1 1，这样的话如果要查询的话我们只需要利用前缀和的方法就能求出来具体的值了

同时既然我们要保留最右边的数，那么对于查询我们应该也要从小到大查，所以我们将询问按右端点升序排序

对于权值数组，其既有单点修改，又有区间查询，显然我们可以使用树状数组维护

对于具体的更新操作，我们用一个 lst 数据记录某个数字上次出现的位置，如果本次查询的范围内某一个数字之前出现过，那么就要消除这个数字的权值，同时更新 lst，否则直径更新当前位置的权值，同时更新 lst

同时注意到对于一个区间如果我们已经修改完了，那么就不需要再次修改了，所以定义一个左边界 l，其代表我们已经修改到什么地方了，防止多余的修改

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937_64 rnd(chrono::steady_clock::now().time_since_epoch().count());class Fenw
{
private:int n;vector<int> tree;public:Fenw(int n) : n(n), tree(n + 1, 0) {}int lowbit(int x) { return x & -x; }void update(int x, int k){for (; x <= n; x += lowbit(x))tree[x] += k;}int query(int x){int res = 0;for (; x; x -= lowbit(x))res += tree[x];return res;}
};struct Q
{int l, r, id;bool operator<(const Q &b) const { return r < b.r; }
} q[1000005];
int a[1000005];
int ans[1000005];
int lst[1000005];
void solve()
{int n;cin >> n;for (int i = 1; i <= n; i++)cin >> a[i];Fenw fw(n);int m;cin >> m;for (int i = 1; i <= m; i++){cin >> q[i].l >> q[i].r;q[i].id = i;}sort(q + 1, q + m + 1);for (int i = 1, l = 1; i <= m; i++){for (int j = l; j <= q[i].r; j++){if (lst[a[j]])fw.update(lst[a[j]], -1);fw.update(j, 1);lst[a[j]] = j;}l = q[i].r + 1;ans[q[i].id] = fw.query(q[i].r) - fw.query(q[i].l - 1);}for (int i = 1; i <= m; i++)cout << ans[i] << '\n';
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;while (t--){solve();}return 0;
}