《理解进制问题--剖析存储底层奥秘》
《专题–进制问题》

🔥小龙报:个人主页
🎬作者简介:C++研发,嵌入式,机器人方向学习者
❄️个人专栏:《C语言》《算法》KelpBar海带Linux智慧屏项目
✨永远相信美好的事情即将发生

文章目录
- 《专题--进制问题》
- 前言
- 一、二进制和进制转换
- 1.1引入
- 1.2二进制转十进制
- 1.2.1权重
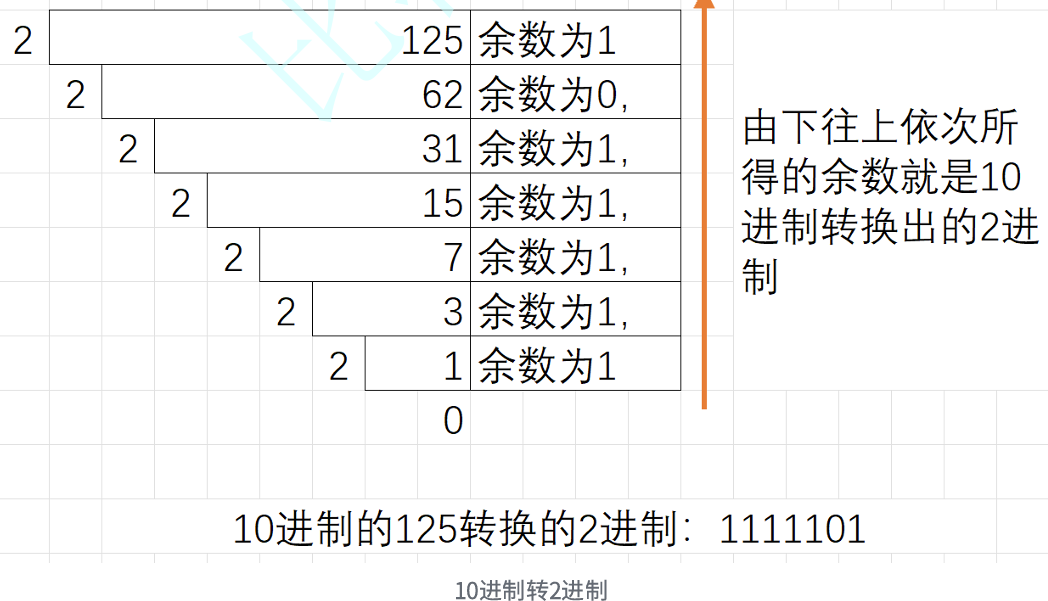
- 1.3 十进制转二进制
- 1.4二进制转十六进制
- 1.5二进制转八进制
- 二、原码、反码、补码
- 三、移位操作符
- 3.1左移操作符 <<
- 3.2右移操作符 >>
- 四、位操作符 &、|、^、~
- 五、综合运用
- 5.1不能创建临时变量(第三个变量),实现两个整数的交换
- 5.2求一个整数存储在内存中的二进制中1的个数。
- 5.3编写代码将13的二进制序列的第5位修改为1,然后再改回0(二进制位置0或者置1)
- 六、总结---每日励志时刻
前言
我们会讲解计算机的二进制,六进制,八进制等知识,让大家更好理解计算机的存储和运行规则
一、二进制和进制转换
1.1引入
其实2进制、8进制、10进制、16进制是数值的不同表⽰形式⽽已。
例:数值15的各种进制的表示形式:

我们重点介绍⼀下⼆进制:
⾸先我们还是得从10进制讲起,其实10进制是我们⽣活中经常使⽤的,我们已经形成了很多尝试:
• 10进制中满10进1,10进制的数字每⼀位都是0~9的数字组成
其实⼆进制也是⼀样的
• 2进制中满2进1,2进制的数字每⼀位都是0~1的数字组成
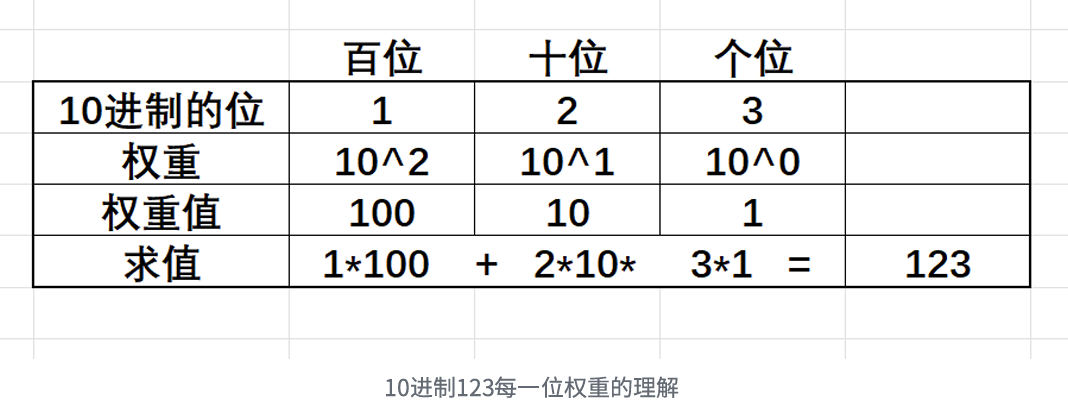
1.2二进制转十进制
1.2.1权重
以123举例
十进制
二进制
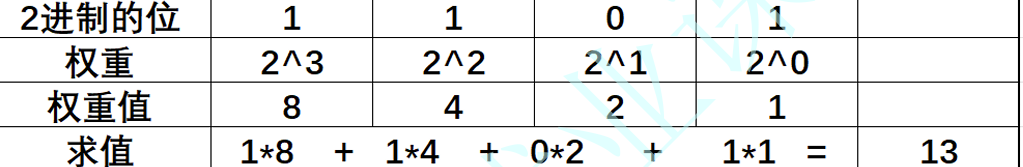
1.3 十进制转二进制
1.4二进制转十六进制
16进制的数字每⼀位是0~9 ,a~f 的,0~9 ,a~f的数字,各⾃写成2进制,最多有4个2进制位就⾜够了,⽐如f的⼆进制是1111,所以在2进制转16进制数的时候,从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位,剩余不够4个⼆进制位的直接换算。
如:2进制的01101011,换成16进制:0x6b,16进制表示的时候前⾯加0x

1.5二进制转八进制
8进制的数字每⼀位是0~7的 ,0~7的数字,各⾃写成2进制,最多有3个2进制位就⾜够了,⽐如7的二进制是111,所以在2进制转8进制数的时候,从2进制序列中右边低位开始向左每3个2进制位会换算⼀个8进制位,剩余不够3个2进制位的直接换算。
如:2进制的01101011,换成8进制:0153,0开头的数字,会被当做8进制

二、原码、反码、补码
(1)整数的2进制表示方法有三种,即原码、反码和补码
(2)有符号整数的三种表⽰⽅法均有符号位和数值位两部分
(3) 2进制序列中,最高位的1位是被当做符号位,剩余的都是数值位。
(4)符号位都是⽤0表示“正”,⽤1示“负”
PS:(重要)
(1)正整数的原、反、补码都相同。
(2)负整数的三种表⽰⽅法各不相同。
(3)原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。
(4)反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
(5)补码:反码+1就得到补码。
(6) 补码得到原码也是可以使⽤:取反,+1的操作
三、移位操作符
注:移位操作符的操作数只能是整数
3.1左移操作符 <<
移位规则: 左边抛弃、右边补0
举例:
#include <stdio.h>
int main()
{int num = 10;int n = num << 1;printf("n= %d\n", n);printf("num= %d\n", num);return 0;
}
运行结果:

解析:

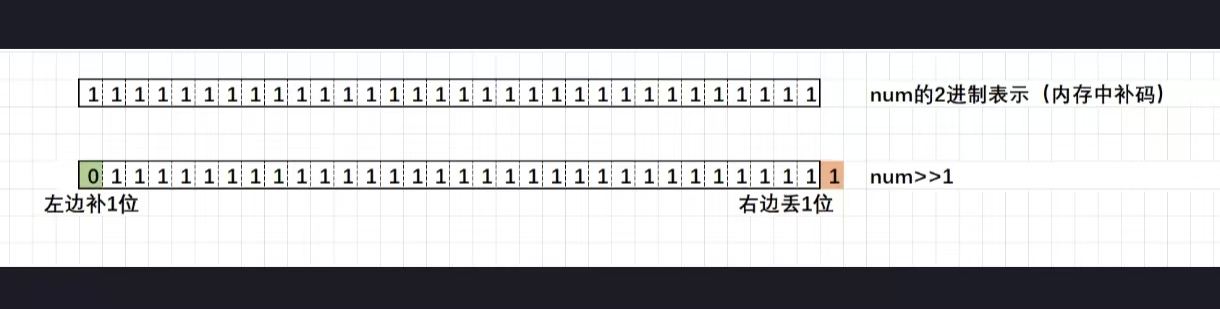
3.2右移操作符 >>
移位规则: 首先右移运算分两种:
(1) 逻辑右移:左边⽤0填充,右边丢弃
(2)算术右移:左边⽤原该值的符号位填充,右边丢弃(巨大多数编辑器遵循的标椎)
#include <stdio.h>
int main()
{int num = 10;int n = num >> 1;printf("n= %d\n", n);printf("num= %d\n", num);return 0;
}
运行结果:

解析:
(1)算数右移

(2)逻辑右移
PS:
(1)对于移位运算符,不要移动负数位,这个是标准未定义的。
(2) 左移一位有乘以2的效果,右移一位有除2的效果
四、位操作符 &、|、^、~
注:移位操作符的操作数只能是整数
例:
#include <stdio.h>
int main()
{int num1 = -3;int num2 = 5;printf("%d\n", num1 & num2);printf("%d\n", num1 | num2);printf("%d\n", num1 ^ num2);printf("%d\n", ~0);return 0;
}
运行结果:
总结:
(1)按位与(&):两个位同时为1时结果才是1,可用于“按位提取”(保留特定位)或“将指定位清零”。
(2)按位或(|):两个位至少有一个为1时结果就是1,可用于“按位设置”(将特定位置为1)。
(3)按位异或(^):两个位不同时结果为1,相同则为0,可用于“按位翻转”(0变1、1变0)或“不借助临时变量交换两个数”。例 x ^ x 结果恒为0。
(4) 按位取反(~):对单个位取反(0变1、1变0),属于单目运算符,会将变量的所有二进制位(包括符号位)反转。
五、综合运用
5.1不能创建临时变量(第三个变量),实现两个整数的交换
前置知识:
按位异或(^):两个位不同时结果为1,相同则为0,可用于“按位翻转”(0变1、1变0),例 x ^ x 结果恒为0且任何数按位异或上0都等于它本身。
代码:
#include <stdio.h>
using namespace std;
int main()
{int a = 10;int b = 20;a = a ^ b;/ a // a = 10^20b = a ^ b; // b = 10^20^20 = 10a = a ^ b; //a = 10^20^10 = 20printf("%d %d", a, b);return 0;
}
运行结果:

5.2求一个整数存储在内存中的二进制中1的个数。
代码:
(1)方法一:缺点无法计算负数
#include <stdio.h>
using namespace std;
int main()
{int a = 10;int cnt = 0;while (a){if (a % 2 == 1)cnt++;a /= 2;}printf("%d", cnt);return 0;
}
(1)方法二:优化点在循环32次
前置知识:(1)按位与(&):两个位同时为1时结果才是1,可用于“按位提取”(保留特定位)或“将指定位清零”。
代码:
#include <stdio.h>
using namespace std;
int main()
{int a = -1;int cnt = 0;for (int i = 0; i < 32; i++){if (a & (1 << i)) //1的二进制位为0001cnt++;}printf("%d", cnt);return 0;
(1)方法三:
前置知识:n & (n - 1)
图解:n & (n - 1)
这个画红圈的表达式能去掉最右边的1,所以这个表达式能执行几次,就有几个1,从最右边的1开始。

代码
#include <>
using namespace std;
int main()
{int a = -1;int cnt = 0;while (a){cnt++;a = a & (a - 1);}printf("%d", cnt);return 0;
}
5.3编写代码将13的二进制序列的第5位修改为1,然后再改回0(二进制位置0或者置1)
13的2进制序列: 00000000000000000000000000001101
将第5位置为1后:00000000000000000000000000011101
将第5位再置为0:00000000000000000000000000001101
前置知识:
按位或(|):两个位至少有一个为1时结果就是1,可用于“按位设置”(将特定位置为1)
按位取反(~):对单个位取反(0变1、1变0),属于单目运算符,会将变量的所有二进制位(包括符号位)反转
代码:
#include <iostream>
using namespace std;
int main()
{int a = 13;a = a | (1 << 4); //修改为1printf("%d\n", a);a = a & ~(1 << 4); //修改为0printf("%d\n", a); return 0;
}
运行结果:

六、总结—每日励志时刻

