2022年ASOC SCI2区TOP，基于竞争与合作策略的金字塔粒子群算法PPSO，深度解析+性能实测，深度解析+性能实测

---

1.摘要

粒子群算法（PSO）已在各类优化问题中展现出显著优势，其核心要素——拓扑结构与更新策略——对算法性能具有决定性影响。本文提出了金字塔粒子群算法（PPSO），通过引入竞争与合作机制来更新粒子信息，该算法构建金字塔分层结构，依据粒子适应度将其分配至特定层级。同一层级内的粒子进行两两竞争，区分优胜者与失败者：失败者与对应优胜者合作，而优胜者则与上层及顶层粒子协同进化。PPSO赋予每个粒子独特的学习能力，使其能够参考多个范例而非仅学习全局最优解，有效增强了种群多样性并提升了算法性能。

2.基于竞争与合作策略的金字塔粒子群算法PPSO

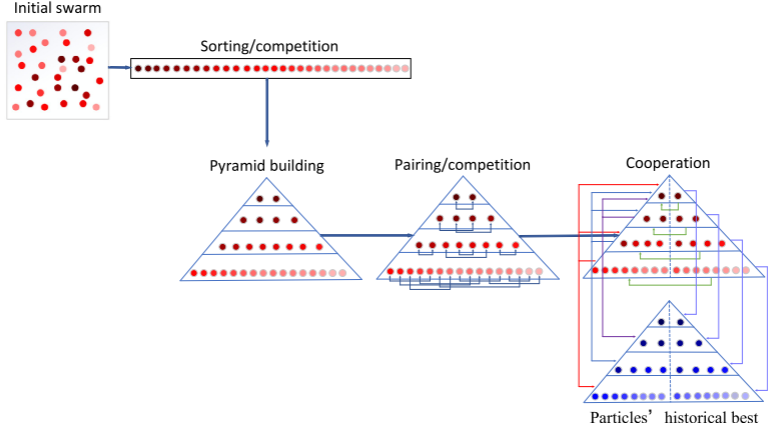
针对标准PSO因仅依赖单一全局最优粒子而易于早熟收敛的缺陷，本文受现实多层管理体系启发，提出了金字塔拓扑结构，该结构依据粒子适应度进行分层，优质粒子居于上层。上层粒子可引导下层，实现了引导责任的均衡分配，从而有效增强了种群多样性，避免了早熟收敛。

PPSO算法引入了双重竞争策略，通过所有粒子按适应度排序划分金字塔层级的全局竞争；在同层粒子间进行随机配对、区分胜败者的局部竞争。胜者可向更高层级学习，而败者仅能向同层胜者学习。这两层竞争机制共同增强了种群的多样性，有效抑制了早熟收敛现象。

各层"败者"除自身最优解外，还会向同层"胜者"学习；而各层"胜者"（顶层除外）则能同时向自身最优解、上层粒子及顶层粒子学习。
$$\{\begin{array}{ll}{V}_{P{L}_{i,j}}^{t+1}=r_1\cdot V_{P{L}_{i,j}}^t+r_2\cdot (B_{P{L}_{i,j}}^t-X_{P{L}_{i,j}}^t)+r_3\cdot (X_{P{W}_{i,j}}^t-X_{P{L}_{i,j}}^t)& \\ X_{P{L}_{i,j}}^{t+1}=X_{P{L}_{i,j}}^t+V_{P{L}_{i,j}}^{t+1}& \end{array}$$
$$\{\begin{array}{ll}{V}_{p{W}_{ij}}^{t+1}& =r_4\cdot V_{p{W}_{ij}}^t+r_5\cdot (B_{p{W}_{ij}}^t-X_{p{W}_{ij}}^t)+r_6\cdot (X_{p_{i-1,k}}^t-X_{p{W}_{ij}}^t)\\ & +\rho \cdot r_7\cdot (X_{p_{1,m}}^t-X_{p{W}_{ij}}^t)\\ X_{p{W}_{ij}}^{t+1}& =X_{p{W}_{ij}}^t+V_{p{W}_{ij}}^{t+1}\end{array}$$

3.结果展示

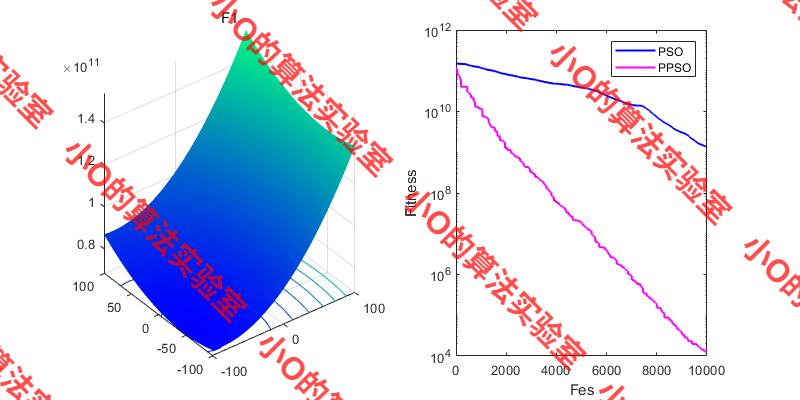
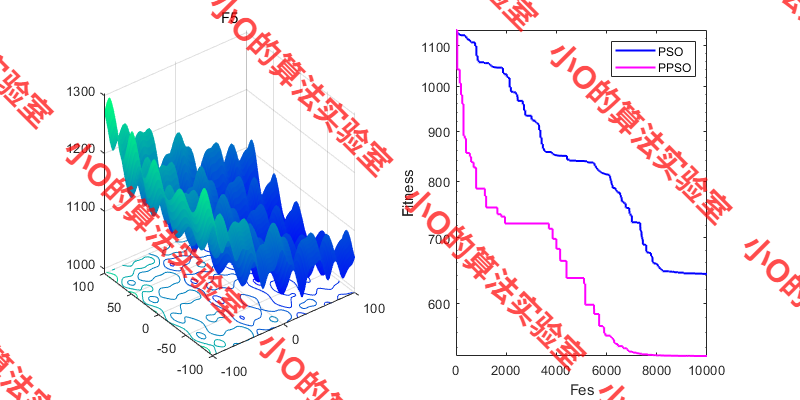
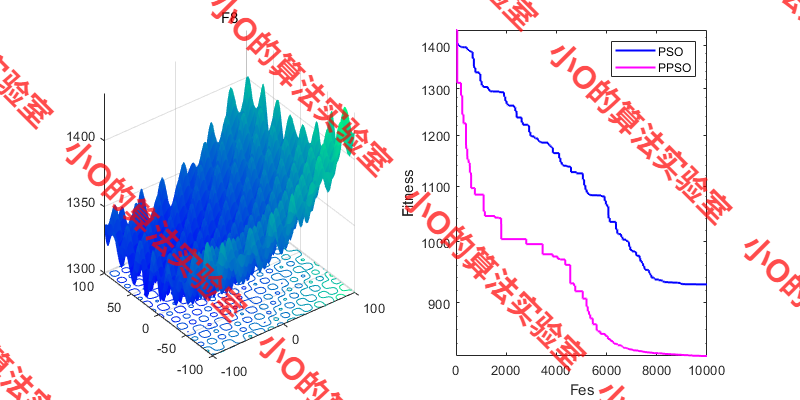
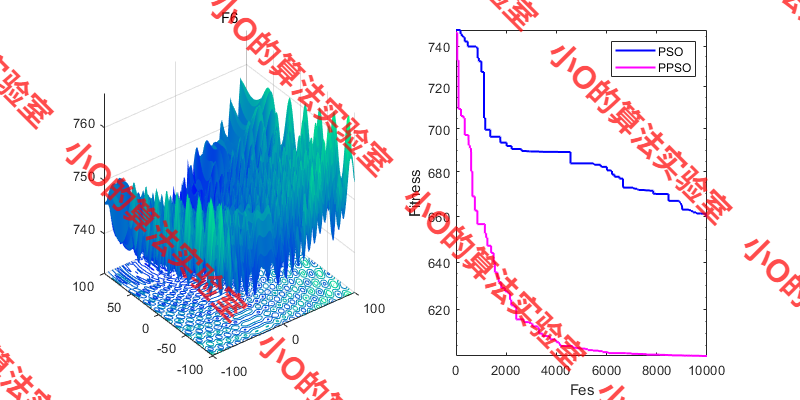
4.参考文献

[1] Li T, Shi J, Deng W, et al. Pyramid particle swarm optimization with novel strategies of competition and cooperation[J]. Applied Soft Computing, 2022, 121: 108731.

5.代码获取

xx

6.算法辅导·应用定制·读者交流

xx