当前位置：首页 > news >正文

数据结构入门 (九)：线索的“寻路”指引 —— 详解线索二叉树

news 2025/10/18 7:00:52

一、引言：一次遍历引发的“血案”
一、一个问题：孩子还是线索？
二、线索二叉树的C语言实现
- 1.头文件
- 2.创建线索二叉树和树节点
- 3.插入节点
- 4.访问节点
- 5.线索化二叉树
- 6.遍历线索二叉树
- 7.释放二叉树
- 8.测试函数
三、总结：空间换效率的经典之作

一、引言：一次遍历引发的“血案”

在上一篇文章中，我们掌握了二叉树的“行走”方式——遍历。通过中序遍历，我们可以得到一个 DBEAC 这样的有序序列。在这个序列中，我们能清晰地知道 D 的后继是 B，A 的前驱是 E。

但这一切，都是“马后炮”。

当遍历结束，我们回到树的原始结构中，站在节点 E 上，如果我们想再次找到它的前驱 B，唯一的办法就是——重新从根节点 A 开始，再完整地遍历一次！

这在需要频繁查找前驱和后继的场景下，简直是一场性能灾难。我们不禁要问：为什么我们不能在“行走”时，就沿途铺设一些“路标”或“导向绳”，让我们能方便地找到前路和后路呢？

就在我们为此苦恼时，我们又发现了另一个问题：在一棵有 n 个节点的二叉链表中，有 n - 1 条边，但总共有 2n 个指针域。这意味着，有 2n - ( n - 1) = n + 1 个指针域是 NULL，它们被白白地浪费掉了！
在这里插入图片描述
一个“性能的痛点”（找不到前驱后继），一个“空间的痛点”（n + 1个空指针）。此时，聪明的你想到了：我们何不利用这些被浪费的空指针，去解决那个性能痛点呢？

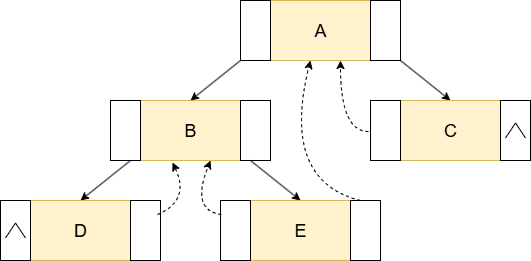
这就是线索二叉树的核心思想：我们利用那些本应指向 NULL 的空指针域，让它们“变废为宝”，转而指向该节点在特定遍历序列（如中序）中的前驱和后继。

指向前驱和后继的指针，称为线索。
利用线索重构的二叉链表，称为线索链表。
二叉链表相应的二叉树，称为线索二叉树。

一、一个问题：孩子还是线索？

想法虽好，但仍然面临考验：我们如何知道某一个节点的 left 指针指向的是左孩子，还是指向前驱的线索？right指针指向右孩子还是指向后继？

为了解决这个“身份识别”的问题：我们必须为每个节点增加两个标志位：

lTag：
- 0：left 指针指向左孩子。
- 1：left 指针指向前驱线索。
rTag：
- 0：right 指针指向右孩子。
- 1：right 指针指向后继线索。

图2：线索化后的二叉树节点结构与示意图

图节点结构与线索化示意图（中序：DBEAC）

二、线索二叉树的C语言实现

1.头文件

typedef int Element;
// 线索二叉树的节点结构
typedef struct treeNode
{Element data;struct treeNode *left;struct treeNode *right;int lTag;   // 0表示left指针指向NULL，1表示left指针指向前驱int rTag;   // 0表示right指针指向NULL，1表示right指针指向前驱
} BTNode;typedef struct
{BTNode *root;int count;
} ThreadedBTree;ThreadedBTree* createThreadedBTree(BTNode *root);
BTNode *createBTNode(Element e);
void releaseThreadedBTree(ThreadedBTree *tree);void insertThreadedBTree(ThreadedBTree *tree, BTNode *parent, BTNode* left, BTNode* right);void visitTbtNode(const BTNode *node);void inOrderThreadingBTree(ThreadedBTree *tree); // 中序线索化的过程void inOrderTbTree(ThreadedBTree *tree); // 线索化后，遍历tree这棵树

2.创建线索二叉树和树节点

ThreadedBTree* createThreadedBTree(BTNode* root)
{ThreadedBTree *tree = malloc(sizeof(ThreadedBTree));if (tree == NULL){fprintf(stderr, "Error allocating threaded btee\n");return NULL;}if (root){tree->root = root;tree->count = 1;} else{tree->root = NULL;tree->count = 0;}return tree;
}BTNode* createBTNode(Element e)
{BTNode *node = malloc(sizeof(BTNode));if (node == NULL){fprintf(stderr, "Error allocating memory\n");return NULL;}node->data = e;node->left = node->right = NULL;node->lTag = node->rTag = 0;return node;
}

3.插入节点

void insertThreadedBTree(ThreadedBTree* tree, BTNode *parent, BTNode* left, BTNode* right)
{if (tree && parent){parent->left = left;parent->right = right;if (left){tree->count++;}if (right){tree->count++;}}
}

4.访问节点

&0xff 是一种C语言技巧，用于确保在处理 char 类型时，如果它被默认当作有符号数，能被正确地当作无符号 int 传递给 printf 的 %c（或 %d），避免因符号扩展导致打印出负数或乱码。

void visitTbtNode(const BTNode* node)
{if (node){printf("\t%c", node->data & 0xff);}
}

5.线索化二叉树

// 全局变量，用于在递归中始终保存“前一个”被访问的节点
static BTNode *pre = NULL;static void inOrderThreading(BTNode *node) {if (node) {// 1. 递归，深入左子树inOrderThreading(node->left);// 2. 检查当前节点的左指针是否为空if (node->left == NULL) {// 如果为空，建立前驱线索node->lTag = 1;node->left = pre;}// 3. 检查“前一个”节点的右指针是否为空if (pre && pre->right == NULL) {pre->right = node;pre->rTag = 1;}// 4. 更新 pre，让 pre 永远指向刚被访问过的节点pre = node;// 5. 递归，深入右子树inOrderThreading(node->right);}
}void inOrderThreadingBTree(ThreadedBTree* tree) {if (tree) {inOrderThreading(tree->root);}
}

6.遍历线索二叉树

线索化最大的好处是什么？是我们可以实现非递归、不使用栈的超高效中序遍历！

void inOrderTbTree(ThreadedBTree* tree) {BTNode *node = tree->root;while (node) {// 一直往左走while (node->lTag == 0) {node = node->left;}// 找到并访问线索化的首节点visitTbtNode(node);// 向右进行中序线索化后的结果// 只要 rTag 是 1，就说明 right 指向的是后继，直接访问while (node->rTag && node->right) {node = node->right;visitTbtNode(node);}// 将这个不是右线索化的节点，当作新节点，再进行循环node = node->right;}
}

7.释放二叉树

在释放节点前要检查 Tag 和 rTag，避免重复释放或误释放线索指向的节点，这比普通树的释放更复杂，通常需要结合后序遍历。

static void freeBTNode(ThreadedBTree *tree, BTNode *node)
{if (node){if (node->lTag == 0){freeBTNode(tree, node->left);}if (node->rTag == 0){freeBTNode(tree, node->right);}free(node);tree->count--;}
}void releaseThreadedBTree(ThreadedBTree* tree)
{if (tree->root){freeBTNode(tree, tree->root);}
}

8.测试函数

#include <stdio.h>
#include <stdlib.h>
#include "threadedBTree.h"ThreadedBTree *setupTree()
{BTNode *nodeA = createBTNode('A');BTNode *nodeB = createBTNode('B');BTNode *nodeC = createBTNode('C');BTNode *nodeD = createBTNode('D');BTNode *nodeE = createBTNode('E');BTNode *nodeF = createBTNode('F');BTNode *nodeH = createBTNode('H');BTNode *nodeG = createBTNode('G');BTNode *nodeK = createBTNode('K');ThreadedBTree *tree = createThreadedBTree(nodeA);insertThreadedBTree(tree, nodeA, nodeB, nodeE);insertThreadedBTree(tree, nodeB, NULL, nodeC);insertThreadedBTree(tree, nodeE, NULL, nodeF);insertThreadedBTree(tree, nodeC, nodeD, NULL);insertThreadedBTree(tree, nodeF, nodeG, NULL);insertThreadedBTree(tree, nodeG, nodeH, nodeK);return tree;
}void test01()
{ThreadedBTree *tree = setupTree();printf("tree node: %d\n", tree->count);inOrderThreadingBTree(tree);printf("show:");inOrderTbTree(tree);releaseThreadedBTree(tree);
}int main() {test01();
}