当前位置：首页 > news >正文

【算法与数据结构】二叉树后序遍历非递归算法：保姆级教程(附具体实例+可运行代码）

news 2025/10/18 13:55:58

刚学二叉树遍历的时候，我总在两个地方卡壳：递归写法虽然简单，但处理大一点的树就容易栈溢出；非递归又搞不懂“节点为啥要入两次栈”——尤其是后序遍历（左→右→根），用栈模拟总把顺序搞反，比如把根节点提前输出，或者漏了右子树遍历。

后来才发现，后序非递归的核心就一个技巧：让节点入两次栈，用一个flag区分“遍历阶段”——第一次入栈是去遍历左子树，第二次入栈是遍历完右子树该输出节点了。今天就把这份实验的解题思路拆成“新手能跟着复现”的版本，附具体二叉树实例和修正后的代码，保证你看完能跑通。

在这里插入图片描述

一、先明确：我们要遍历的二叉树长啥样？（实验实例）

实验里用的二叉树结构很典型，先把它画清楚，后续所有操作都围绕这个实例展开，避免抽象：
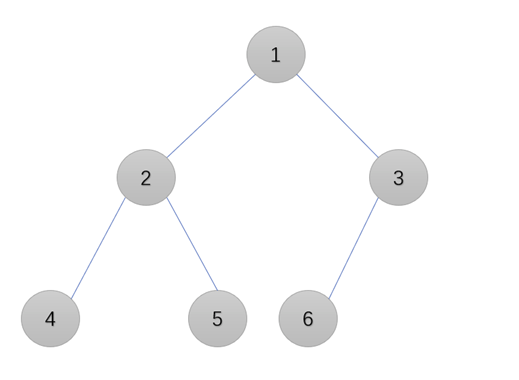
在这里插入图片描述

根节点：1
左子树：节点2，它的左孩子4、右孩子5（4和5都是叶子节点，无后代）
右子树：节点3，它的左孩子6（右孩子为NULL，叶子节点）
后序遍历的正确结果应该是：4 → 5 → 2 → 6 → 3 → 1（左子树→右子树→根）

二、核心思路：为什么要“节点入两次栈+flag标志”？

后序遍历的难点是“根节点要最后输出”，但栈是“先进后出”的，直接入栈会导致根节点先出来。所以用“两次入栈+flag”解决：

flag=0：第一次入栈，代表“还没遍历左子树”——此时不能输出节点，要先把它压栈，去遍历它的左子树；
flag=1：第二次入栈，代表“左子树遍历完了，刚遍历完右子树”——此时可以输出节点了。

简单说：flag就是给节点贴的“任务标签”，0是“先去处理左孩子，我等着”，1是“左、右孩子都处理完了，该处理我了”。

三、完整代码

#include <stdio.h>
#include <stdlib.h>#define STACK_SIZE 20  // 栈的最大容量，足够存实验中的二叉树节点
int top = -1;  // 栈顶指针（-1表示空栈）// 1. 定义二叉树节点结构
typedef struct MyBiTNode {int data;                  // 节点值struct MyBiTNode *lchild;  // 左孩子指针（修正原文的1child）struct MyBiTNode *rchild;  // 右孩子指针
} BiTNode;// 2. 创建实验用的二叉树（对应上面的实例）
BiTNode *CreateBiTree() {// 根节点1BiTNode *root = (BiTNode*)malloc(sizeof(BiTNode));root->data = 1;root->lchild = NULL;root->rchild = NULL;// 左孩子2root->lchild = (BiTNode*)malloc(sizeof(BiTNode));root->lchild->data = 2;root->lchild->lchild = NULL;root->lchild->rchild = NULL;// 右孩子3root->rchild = (BiTNode*)malloc(sizeof(BiTNode));root->rchild->data = 3;root->rchild->lchild = NULL;root->rchild->rchild = NULL;// 节点2的左孩子4root->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));root->lchild->lchild->data = 4;root->lchild->lchild->lchild = NULL;root->lchild->lchild->rchild = NULL;// 节点2的右孩子5root->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));root->lchild->rchild->data = 5;root->lchild->rchild->lchild = NULL;root->lchild->rchild->rchild = NULL;// 节点3的左孩子6root->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));root->rchild->lchild->data = 6;root->rchild->lchild->lchild = NULL;root->rchild->lchild->rchild = NULL;return root;
}// 3. 定义栈元素结构（存节点指针+flag标志）
typedef struct StackNode {BiTNode *node;  // 二叉树节点指针int flag;       // 标志：0=第一次入栈，1=第二次入栈
} StackNode;// 4. 入栈操作
void push(StackNode *stack, BiTNode *node, int flag) {if (top >= STACK_SIZE - 1) {printf("栈满了，无法入栈！\n");return;}top++;stack[top].node = node;stack[top].flag = flag;
}// 5. 出栈操作（修正原文：添加top--）
StackNode pop(StackNode *stack) {StackNode empty = {NULL, -1};  // 空栈返回值if (top == -1) {printf("栈空了，无法出栈！\n");return empty;}StackNode res = stack[top];top--;  // 栈顶指针下移（原文漏了这步）return res;
}// 6. 输出节点值（辅助函数）
void display(BiTNode *node) {printf("%d ", node->data);
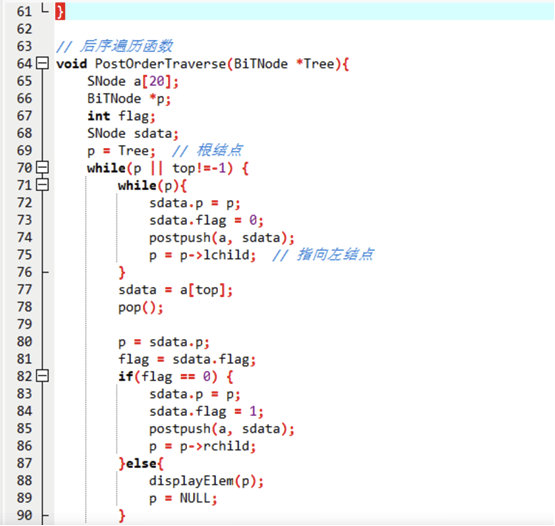
}// 7. 核心：后序遍历非递归算法
void PostOrderTraverse(BiTNode *root) {StackNode stack[STACK_SIZE];  // 定义栈BiTNode *current = root;      // 当前遍历的节点// 循环条件：当前节点非空 或 栈非空while (current != NULL || top != -1) {// 第一步：遍历左子树，所有节点带flag=0入栈while (current != NULL) {push(stack, current, 0);  // 第一次入栈，flag=0（去遍历左子树）current = current->lchild;  // 向左子树移动}// 第二步：出栈，判断flagStackNode popNode = pop(stack);current = popNode.node;  // 获取出栈的节点int flag = popNode.flag;if (flag == 0) {// 第一次出栈：左子树遍历完，改flag=1重新入栈（准备遍历右子树）push(stack, current, 1);current = current->rchild;  // 向右子树移动} else {// 第二次出栈：右子树遍历完，输出节点（左→右→根的最后一步）display(current);current = NULL;  // 输出后，当前节点置空，避免重复遍历}}
}// 主函数：测试
int main() {BiTNode *root = CreateBiTree();printf("二叉树后序遍历（非递归）结果：");PostOrderTraverse(root);printf("\n");return 0;
}

在这里插入图片描述

四、实例遍历流程拆解（跟着走一遍就懂了）

结合我们的二叉树实例（根1），一步步看非递归是怎么跑的，重点看栈的变化和flag的作用：

步骤1：遍历左子树，节点带flag=0入栈

current=1（根）→ 入栈（node=1, flag=0）→ current=1的左孩子2；
current=2 → 入栈（node=2, flag=0）→ current=2的左孩子4；
current=4 → 入栈（node=4, flag=0）→ current=4的左孩子NULL（左子树遍历完）。

此时栈内元素（从栈底到栈顶）：(1,0) → (2,0) → (4,0)，top=2。

步骤2：出栈处理（flag=0→改1入栈，遍历右子树）

出栈(4,0) → flag=0 → 重新入栈(4,1) → current=4的右孩子NULL（右子树为空）；
出栈(4,1) → flag=1 → 输出4 → current=NULL；
出栈(2,0) → flag=0 → 重新入栈(2,1) → current=2的右孩子5；
current=5 → 入栈(5,0) → current=5的左孩子NULL（左子树空）；
出栈(5,0) → flag=0 → 重新入栈(5,1) → current=5的右孩子NULL（右子树空）；
出栈(5,1) → flag=1 → 输出5 → current=NULL；
出栈(2,1) → flag=1 → 输出2 → current=NULL。

此时输出：4 5 2，栈内剩余(1,0)，top=0。

步骤3：处理根节点的右子树

出栈(1,0) → flag=0 → 重新入栈(1,1) → current=1的右孩子3；
current=3 → 入栈(3,0) → current=3的左孩子6；
current=6 → 入栈(6,0) → current=6的左孩子NULL（左子树空）；
出栈(6,0) → flag=0 → 重新入栈(6,1) → current=6的右孩子NULL（右子树空）；
出栈(6,1) → flag=1 → 输出6 → current=NULL；
出栈(3,0) → flag=0 → 重新入栈(3,1) → current=3的右孩子NULL（右子树空）；
出栈(3,1) → flag=1 → 输出3 → current=NULL；
出栈(1,1) → flag=1 → 输出1 → current=NULL。

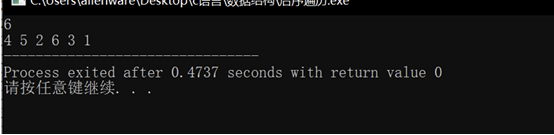
最终输出：4 5 2 6 3 1，和预期一致！
在这里插入图片描述

五、注意点

flag含义搞反：把flag=0当成“该输出”，flag=1当成“遍历左子树”——记住：flag=0是“先处理孩子”，flag=1才是“处理自己”；
栈操作漏了top变化：原文pop函数没写top--，导致栈顶一直不变，遍历会无限循环；
二叉树节点指针错误：创建节点时把lchild写成1child（数字1），编译直接报错；
current置空忘记：输出节点后没把current=NULL，会导致重新遍历左子树，陷入死循环。

六、总结：非递归vs递归，该怎么选？

对比维度	递归写法	非递归写法（本文）
代码复杂度	简单（3行核心逻辑）	稍复杂（需管理栈和flag）
栈空间消耗	依赖系统递归栈（易溢出）	自定义栈（可控）
适用场景	小规模二叉树	大规模二叉树
调试难度	难（栈帧看不见）	易（可打印栈内元素）