当前位置：首页 > news >正文

三种思路彻底掌握 BST 判断（递归与迭代全解析）——力扣98.验证二叉搜索树

news 2025/10/17 5:52:10

力扣98.验证二叉搜索树

验证二叉搜索树（Validate Binary Search Tree）题解大全

一、题目描述

给定一个二叉树的根节点 root，判断它是否是一棵有效的二叉搜索树（BST）。

有效二叉搜索树的定义：

节点的左子树只包含严格小于当前节点的值；
节点的右子树只包含严格大于当前节点的值；
所有左子树和右子树本身也必须是二叉搜索树。

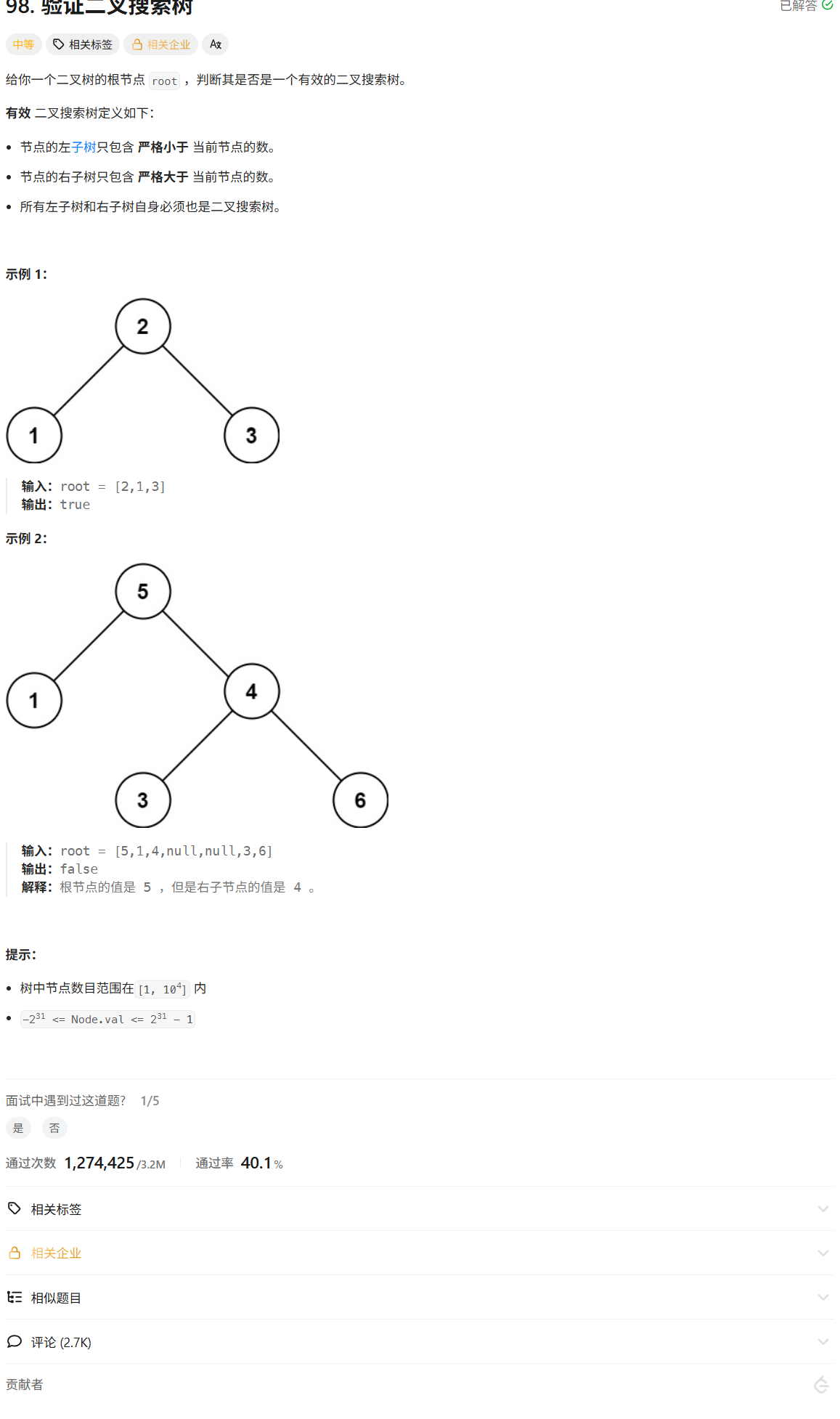
示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5，但其右子树中的节点 4 小于 5。

提示：

节点总数范围：[1, 10⁴]
节点值范围：[-2³¹, 2³¹ - 1]

二、思路分析

判断是否为二叉搜索树，本质上有两种思路：

区间递归法： 每个节点的值必须在一个动态变化的 (min, max) 范围内；
中序遍历法： 二叉搜索树的中序遍历序列应严格递增。

这两种思路都能达到 O(n) 的时间复杂度，区别在于递归参数设计与思维方式不同。

三、解法一：递归区间法（Top-Down）

核心思想：
从根节点开始，为每个节点维护一个允许取值的上下界：

对左子树而言，最大值应为当前节点值；
对右子树而言，最小值应为当前节点值。

若某个节点值不在范围内，则立即返回 false。

代码实现：

class Solution {public boolean isValidBST(TreeNode root) {return validate(root, Long.MIN_VALUE, Long.MAX_VALUE);}private boolean validate(TreeNode node, long min, long max) {if (node == null) return true;if (node.val <= min || node.val >= max) return false;return validate(node.left, min, node.val) && validate(node.right, node.val, max);}
}

在这里插入图片描述

复杂度分析：

时间复杂度：O(n)，每个节点访问一次；
空间复杂度：O(h)，h 为树的高度（最坏 O(n)）。

思维亮点：

使用 long 避免边界越界；
“上下界随递归动态变化”的设计思路极具通用性。

四、解法二：中序遍历法（Inorder Traversal）

核心思想：
二叉搜索树的中序遍历结果是一个严格递增序列。

因此，只需在遍历过程中比较当前节点值是否大于前一个节点值即可。

代码实现：

class Solution {private long prev = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if (root == null) return true;if (!isValidBST(root.left)) return false;if (root.val <= prev) return false;prev = root.val;return isValidBST(root.right);}
}

在这里插入图片描述

复杂度分析：

时间复杂度：O(n)
空间复杂度：O(h)

思维亮点：

利用 BST 的中序有序性质；
实现极为简洁，逻辑清晰。

五、解法三：迭代中序法（使用显式栈）

核心思想：
用栈模拟中序遍历过程，每次取出最左节点，与前驱节点比较。

代码实现：

import java.util.Stack;class Solution {public boolean isValidBST(TreeNode root) {Stack<TreeNode> stack = new Stack<>();TreeNode curr = root;long prev = Long.MIN_VALUE;while (curr != null || !stack.isEmpty()) {while (curr != null) {stack.push(curr);curr = curr.left;}curr = stack.pop();if (curr.val <= prev) return false;prev = curr.val;curr = curr.right;}return true;}
}

在这里插入图片描述

复杂度分析：

时间复杂度：O(n)
空间复杂度：O(n)

思维亮点：

无递归调用栈；
适合面试场景手写；
清晰体现中序遍历过程。

六、方法对比总结

方法	思路核心	实现方式	是否递归	是否利用中序有序性	时间复杂度	空间复杂度	特点
区间递归法	动态上下界限制	递归	✅	❌	O(n)	O(h)	思维直观、通用性强
中序递归法	严格递增序列	递归	✅	✅	O(n)	O(h)	简洁优雅、代码最短
迭代中序法	栈模拟中序	迭代	❌	✅	O(n)	O(n)	面试友好、结构清晰